改进的电导增量法在光伏系统MPPT中的应用

蔡明想,姜希猛,谢巍

(1.华南理工大学 自动化科学与工程学院,广东 广州 510640;2.中国科学技术大学 工程科学学院,安徽 合肥 230026)

1 引言

太阳能由于其明显的优点越来越受到关注,其主要的利用方式为光伏并网发电[1]。

为了提高光伏发电系统的转换效率,研究高效的最大功率跟踪(MPPT)算法是非常必要的。目前,常用的最大功率跟踪算法有:固定电压(CV)法[2],扰动观测(P&O)法[3],电导增量(INC)法[4]等。CV法实现简单,具有良好的可靠性和稳定性,但是只能固定在最大功率点附近工作。INC法实质上是一种改进的P&O法,这两种算法因转化效率高而得到了广泛应用,但是在天气快速变化的情况下会产生误判,导致系统的工作点远离其最大功率点;而且均采用定步长的方式,难以兼顾跟踪的快速性以及系统稳定性两方面的要求[5]。针对上面这些问题,本文提出了一种改进的MPPT控制方法,最后通过仿真表明该方法的可行性,提高了转换效率。

2 光伏阵列的特性

在考虑光照强度变化和温度影响时,太阳能电池的数学模型为[6]

其中

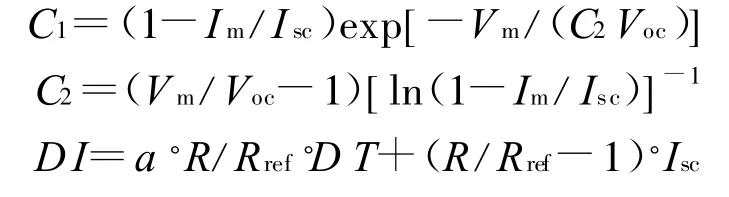
式中:Rref,Tref分别为光照强度和光伏阵列温度参考值,一般取为1 kW/m2,25℃;a为电流变化温度系数,A/℃;b为电压变化温度系数,V/℃;Rs为光伏阵列的串联电阻,Ω;Voc为开路电压,V;Vm为最大功率点电压,V;Isc为短路电流,A;Im为最大功率点电流,A。

运用上述模型对某太阳能电力有限公司的光伏模块STP175S224/Ac进行仿真分析,其主要参数为:Voc=44.2 V,Vm=35.2 V,Isc=5.2 A,Im=4.95 A,Rs=0.65 Ω,a=0.015,b=0.7。

图1和图2分别为光伏阵列在不同光照强度和极板温度下的P-V和I-V曲线。从图1、图2中可知其输出特性是非线性的。当温度上升时,输出最大功率和最大功率点处对应的电压均减小;当光照减小时,输出最大功率和最大功率点处对应的电压也均减小。

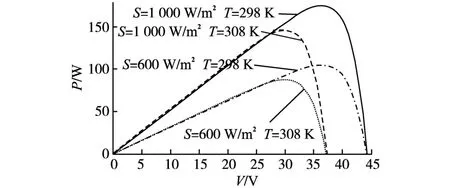
图1 不同光照和温度下的 P-V曲线Fig.1 P-V curves under different illumination and temperature

图2 不同光照和温度下的 I-V曲线Fig.2 I-V curves under different illumination and temperature

3 最大功率跟踪算法

由光伏电池输出特性可知,光伏阵列有一个最大功率点(MPP),它取决于电池板温度和光照大小,不同的温度和光照条件下光伏阵列的最大功率点不同。即使在同一温度和光照条件下,也会使太阳能电池输出功率不同。要使光伏电池尽可能地工作在最大功率点,需要使用最大功率点跟踪(MPPT)控制。

3.1 传统电导增量法

电导增量法判断的依据为当光伏阵列的P-V曲线的斜率为零时在MPP点,为正时在MPP点左边,为负时在MPP点右边。即

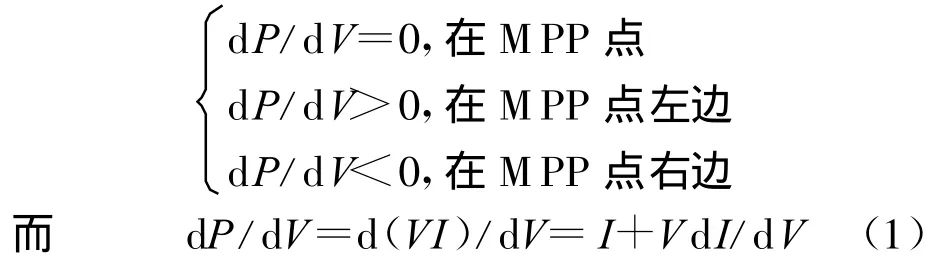
因此可通过判断I+VdI/dV的符号来实现跟踪策略[7]。假设在最大功率点Vref等于VMPP,光伏阵列将维持在这个点直到dI发生变化,然后通过增加或者减少Vref跟踪新的最大功率点。其流程图如图3所示,其中V(K),I(K)分别表示当前检测到的光伏阵列的输出电压和输出电流,V(K-1),I(K-1)分别表示上一次检测到的输出电压和输出电流,Vref表示光伏阵列输出电压参考值,ΔV表示跟踪步长。

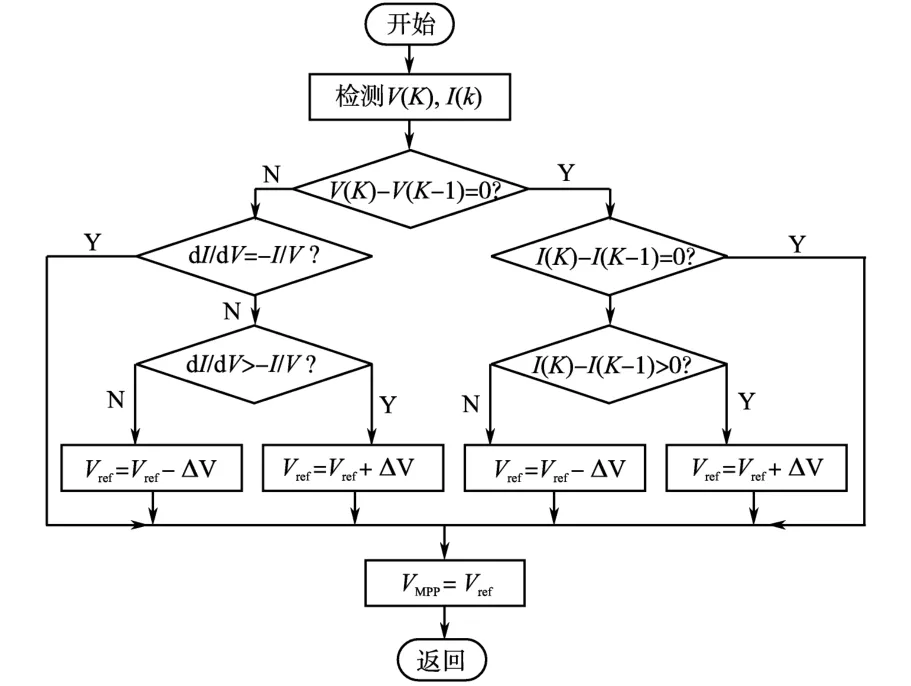
图3 传统电导增量法的流程图Fig.3 Flowchart of the traditional INC method

3.2 改进型电导增量法

传统的电导增量法采用固定步长。当步长选择较大时,对光照变化跟踪速度快,但振荡比较严重,导致稳态误差较大,无法满足系统的稳态要求;当步长选择较小时,振荡现象有所减弱,但对光照变化的跟踪速度变慢,无法满足系统的动态要求。同时传统电导增量法含有复杂的除法计算,这对于数字处理器的实时处理影响较大,影响到了执行的效率和正确性。

鉴于固定步长的缺陷,在此采用变步长方式,且取步长为K|dP/dV|,其中K为固定系数。变步长的电导增量法原理是:当实际工作点离最大功率点较远时,斜率较大,系统跟踪的步长较大;反之,则斜率较小,系统跟踪的步长较小。这样就可以解决固定步长带来的问题。

为了去除除法运算,可以对式(1)进行处理,两边同时除以I,可以得到:

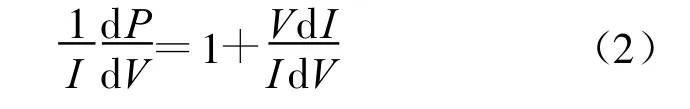
首先判断式(2)中dV的符号,进而判断IdV+VdI的符号,最后通过判断dP/dV的符号来决定输出电压参考值应该增加、减小还是保持不变。其流程图如图4所示。通过结合固定电压法,首先采样当前光伏阵列开路电压值Voc,由于光伏阵列MPP处的电压约为开路电压的0.78倍[8],因此系统将0.78Voc作为初始基准值,控制输出电压移动到MPP电压附近,然后启动变步长电导增量法,实现精确的MPPT控制。

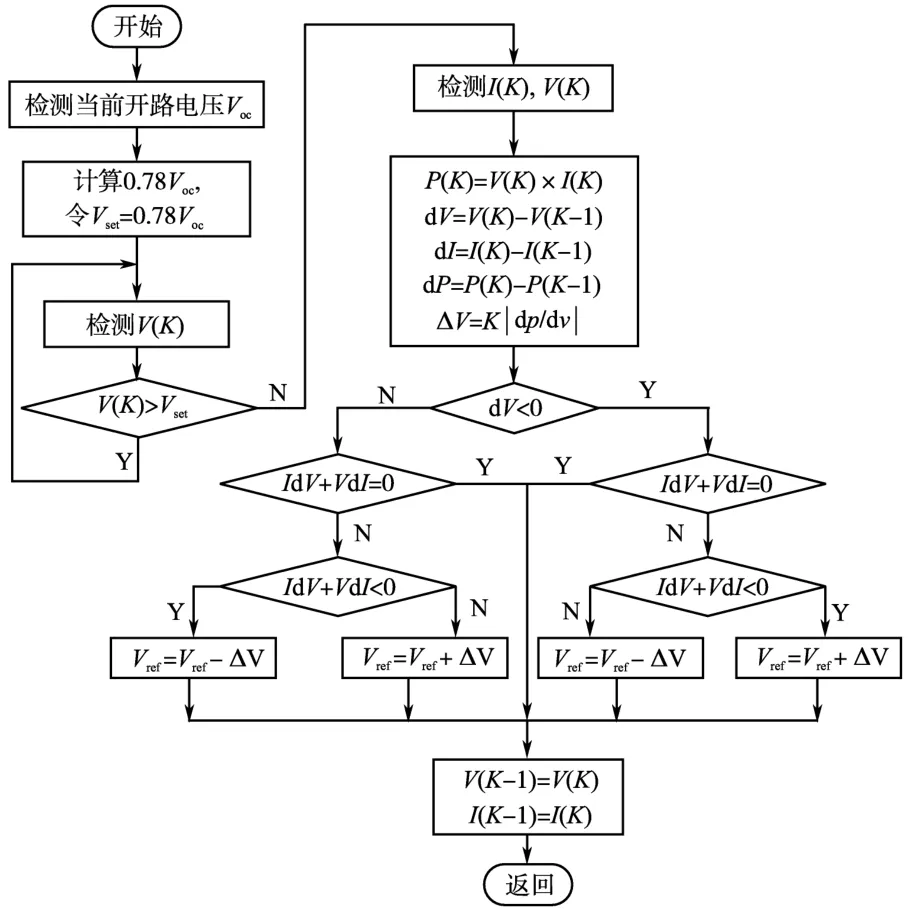
图4 改进型电导增量法流程图Fig.4 Flowchart of the improved INC method

4 最大功率点跟踪控制的仿真

本文以Boost变换器作为DC/DC变换电路,建立了基于改进型电导增量法的仿真模型如图5所示。图5中R,L,C,C1的值分别为50 Ω,0.000 4 H,0.001 F,0.000 5 F。

其控制过程如下:检测到的当前光伏阵列工作点的电压和电流值,通过S-Function和脉宽调制模块得到占空比不同的脉宽调制波以控制DC/DC变换器中IGBT功率开关管的开通与关断,以达到阻抗匹配,从而实现太阳能电池阵列的最大功率跟踪。

图5 M PPT仿真模型Fig.5 Simulation model of MPP T

在标准状态25℃,1 kW/m2,采用两种控制方法仿真所得光伏阵列的输出功率、电压波形如图6所示。从图6可以看出,采用改进的方法,其输出功率能在0.1 s内稳定在最大功率点,且波动比传统INC小很多,稳态精度高达98%,提高了光伏阵列的转换效率。

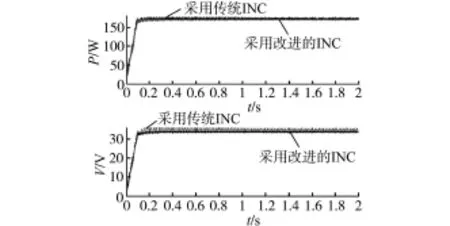
图6 标准状态下,光伏阵列输出功率、电压波形Fig.6 Waveforms of output power,voltage under standard state

图7给出了在光强恒定(1 kW/m2),温度在0.8 s时突然从25℃升到30℃,又在1.6 s时突然从30℃升到35℃的光伏阵列的输出功率、电压的波形。从图7中可以看出,当温度快速变化时,采用改进的方法能快速、平稳、准确地跟踪最大功率点。且光伏阵列的功率、电压随温度的变化情况也符合前面建模所仿真出的输出特性。

图8给出了在温度恒定(25℃),光照强度在0.8 s时突然从1 kW/m2降到0.8 kW/m2,又在1.6 s时突然从0.8 kW/m2降到0.6 kW/m2的光伏阵列的输出功率、电压的波形。从图8中可以看出,当采用改进的方法时,光伏阵列的输出功率、电压均能快速、精准地跟踪变化,且振荡小,稳态精度高。

图7 温度快速变化时光伏阵列输出功率、电压波形Fig.7 Waveforms of output power,voltage under the rapid change temperature

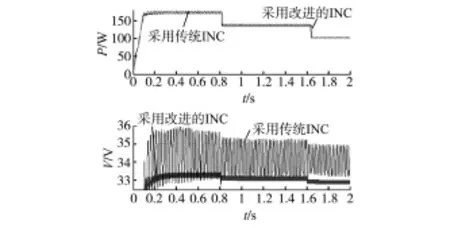
图8 光强快速变化时光伏阵列输出功率、电压波形Fig.8 Waveforms of output power,voltage under the rapid change illumination

5 结论

本文针对传统电导增量法的缺点,结合固定电压法的优点,提出了一种改进的电导增量法,并通过Matlab/Simulink进行了实验仿真,通过分析可以看出该方法能在外界环境快速变化的情况下,保证光伏阵列快速、精确地跟踪最大功率点,且在最大功率点附近的振荡极小,稳态精度较高。仿真和实验结果均表明该方法的可行性和精确性。

[1]刘飞,段善旭,殷进军.单级式光伏发电系统MPPT的实现与稳定性研究[J].电力电子技术,2008,42(3):28-30.

[2]张波,郑宏,曹丰文,等.LED光伏路灯系统的研究与设计[J].电气传动,2010,40(9):38-40.

[3]Roberto F Coelho,Filipe Concer,Denizar C Martins.A Study of the Basic DC-DC Converters Applied in Maximum Power Point T racking[C]∥Power Electronics Conference,COBEP,2009:673-678.

[4]Elgendy M A,Zahawi B,Atkinson D J.Analysis of the Performance of DC Photovoltaic Pumping Systems with Maximum Power Point Tracking[C]∥4th IET Conference on Power Electronics,Machines and Drives,PEMD,2008:426-430.

[5]高吉磊,贺明智,郑琼林.天气变化时光伏并网系统MPPT算法的仿真研究[J].系统仿真学报,2010,22(4):1000-1005.

[6]茆美琴,余世杰,苏建徽.带有 M PPT功能的光伏阵列M atlab通用仿真模型[J].系统仿真学报,2005,17(5):1248-1251.

[7]张峥,男海鹏.基于Matble/Simulink的两级式光伏并网系统仿真分析[J].可再生能源,2010,28(1):81-84.

[8]Hu Jing,Zhang Jiancheng,Wu Hongbo.A Novel MPPT Control Algorithm Based on Numerical Calculation for PV Generation Systems[C]∥IEEE 6th International of Power Electronics and Motion Control Conference,2009:2103-2107.