凸极永磁同步电机电流控制方法研究

吉智,何凤有

(中国矿业大学 信息与电气工程学院,江苏 徐州 221008)

1 引言

凸极永磁同步电机(salient pole permanent magnet synchronous motor,以下简称SPPMSM)具有d轴和q轴电感不相等的特性,其转子形式包括插入式和内装式2种[1]。SPPMSM电机采用合适的控制方法,能够充分利用磁阻转矩来提高输出转矩,具有体积小、结构紧固、适于高速运转的特点[2]。在要求高效率、高精度、大传动比的高性能传动领域受到了广泛关注。

电机高性能调速系统的关键是实现对电机瞬时力矩的控制,而对电机输出转矩的控制最终可以归结为对电机d轴和q轴电流分量的控制[3]。但对于任一给定的转矩,交、直轴电流分量可以有多种不同的组合,而不同的组合方式,所获得的转矩、端电压等特性都不尽相同[4]。因而如何根据给定的力矩和性能要求确定电机d轴和q轴电流分量就构成了电机的电流控制策略问题[5]。

本文针对一类具有凸极性的永磁同步电机,采用理论分析和仿真相结合的方法,对4种电流控制方法进行了研究,包括:id=0、定子电流最小、单位功率因数、恒磁链[6]。深入研究了4种控制方法在不同负载和速度条件下的输出转矩、端电压、功率因数、去磁因数和效率5种特性,以期在不同运行状态下,能够合理选择较佳的电流控制策略,提高调速系统的性能。

2 SPPMSM数学模型

SPPMSM是一个非线性、强耦合的多变量系统,常使用随电机转子磁场同步旋转的 dq轴数学模型。沿用理想电机模型的一系列假设[7],可以推导出如下SPPMSM数学模型。

定子电压方程为

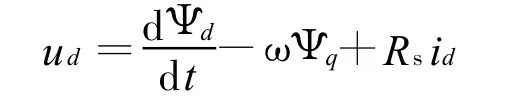
特别地,在稳态下d轴和q轴电流均不变,上式中的第1项均为零,可以简化为

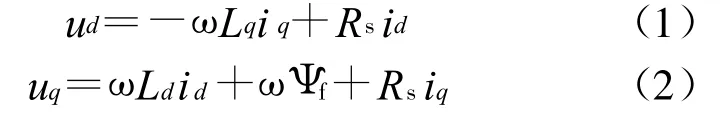
输出转矩为

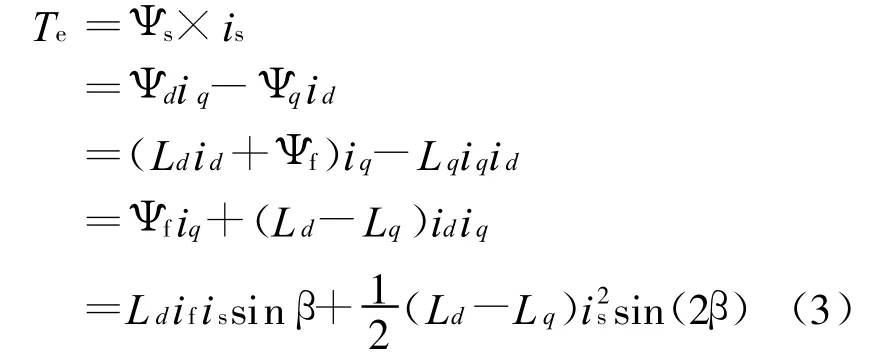
根据以上数学模型可以画出图1电机空间矢量图,其中e0为永磁基波磁场产生的空载反电势,e0=ωrΨf;δ为功角;φ为内功率因数角;φ为功率因数角。

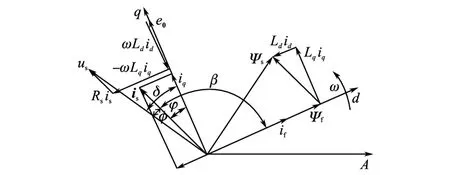
图1 凸极永磁同步电机空间矢量图Fig.1 Space vector diag ram of SPPMSM

由图1可见,电机端电压为

功率因数为

去磁因数定义为d轴电枢反应磁链和永磁磁链的比值[8]:

电机效率定义为电机输出机械功率和输入电功率的比值:

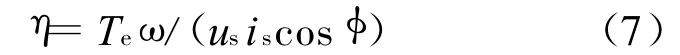
式中:Ψf,Ψs分别为转子永磁磁链、全磁链;Ld,Lq为d,q轴电枢电感;is,id,iq,if分别为电枢电流、电枢电流d轴分量、电枢电流q轴分量、永磁等效励磁电流;us,ud,uq分别为电枢端电压、端电压d轴分量、端电压q轴分量;ω为感应磁场角速度;Rs为电枢绕组电阻。

3 电流控制方法

由式(3)可见永磁同步电机的转矩分成2个部分[9]:第1部分 Ψfiq称为永磁转矩,由定子电流和永磁磁场相互作用产生;第2部分(Ld-Lq)×idiq称为磁阻转矩,由转子凸极效应引起。如果能够独立控制id和iq的大小,也就相当于同时控制了定子电流矢量is的大小和方向,从而实现了对转矩的控制,此即为永磁同步电机矢量控制,或者称为电流相角控制的基本思想[8]。此类调速系统一般是由电机和逆变器构成的,因而电机的转矩、功率、速度等特性自然受逆变器供电能力的制约,但在不超出逆变器供电极限的范围内,对于给定的转矩仍然可以按照不同的规律去分别控制定子电流d轴和q轴两个分量的大小,从而使调速系统的特性满足某些特定的要求,这便产生了不同的电流控制方法[8]。

3.1 id=0控制

id=0控制,即控制定子电流is的方向,使其d轴电流分量为零。由图1可见此时β=90°,is=iq也即is落在 q轴上,所以 φ=0。由式(3)可得:

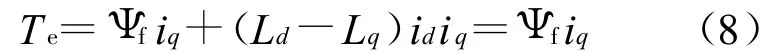
由于 Ψf是常数,显然 Te和iq成线性正比关系,从这一点来看,转矩 Te没有最大值限制,当然实际上最终也要受到逆变器极限馈电能力的限制。将式(1)和式(2)代入式(4)可得:

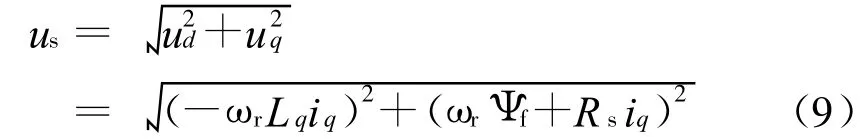
显然当iq增大时,端电压us增大得更快。

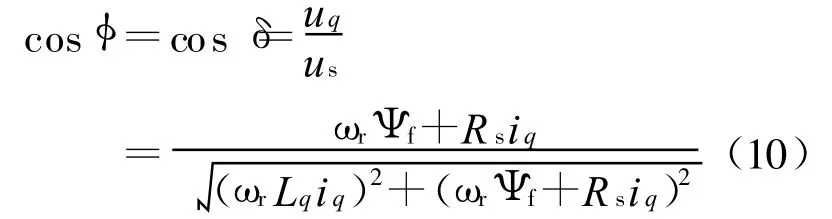
忽略定子电阻,显然随着iq的增大,功率因数变小。由于 d轴电流为零,因此没有去磁效应,去磁因数为零。

3.2 定子电流最小控制

定子电流最小控制,又称为“转矩电流比最大控制”,实际上这种控制方式的目的是要在转矩给定的情况下,合理配置d轴和q轴2个电流分量的大小,使合成的定子电流矢量is最小[10]。这实际上是一个极值问题,将 id=issin β和iq=iscos β代入式(3),并令 dT/dβ=0,d2T/dβ2＜0得:

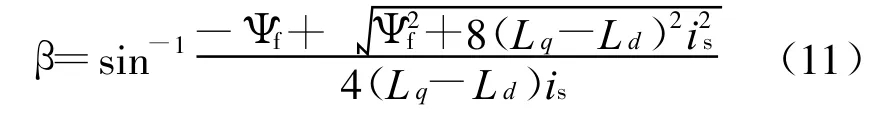
对于一般结构的凸极永磁同步电机Lq=(2～4)Ld[7],即对于任一给定转矩,当β满足式(11)时,定子电流is最小。其实对于隐极的表面式永磁同步电机Lq=Ld,由于式(11)中分子比分母趋向于零的速度更快,结合图1可以推出β=π/2,因此表面式永磁同步电机定子电流最小控制实际上就是id=0控制。

3.3 单位功率因数控制

单位功率因数控制,即控制定子电流的d轴和q轴分量大小,使定子电流is和定子电压us同相,从而δ=φ,φ=0,cos φ=1。由图 1可得 :

将id=issin β和 iq=iscos β代入式(1)和式(2),再代入式(12),解得:

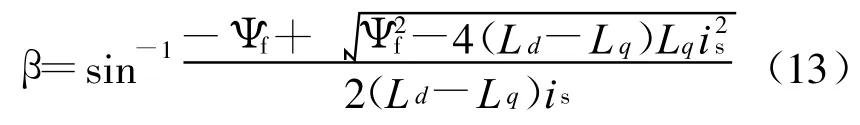
即对于任一给定转矩,当β满足式(13)时,电机功率因数为1。

3.4 恒磁链控制

对于永磁同步电机,永磁磁链是恒定的,但电枢反应造成了全磁链的变化,所以可以通过控制定子电流d轴和q轴分量,使得全磁链和永磁磁链相等,即 Ψs=Ψf[6],也即:

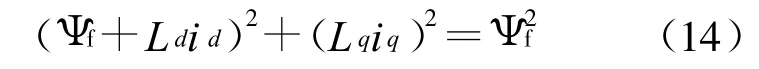
将id=issin β 和 iq=iscos β 代入式(14),解得:

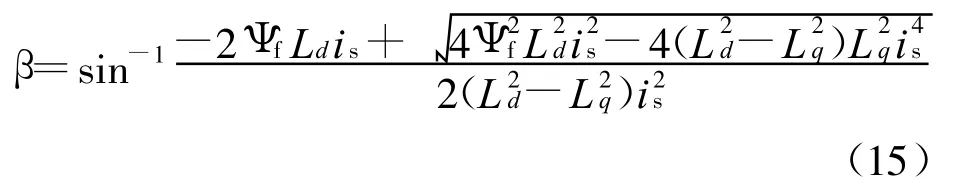
即对于任一给定转矩,当β满足式(15)时,气隙磁链和永磁磁链相等。

4 仿真模型

在永磁同步电机仿真研究中,很多文献将转速和电流信号分别反馈给转速控制器和电流控制器,再由逆变器为永磁同步电机供电,构成典型的转速、电流双闭环控制系统[11- 16]。但利用这种模型对永磁同步电机电流控制算法进行仿真研究,其效果并不好,因为控制系统中包含了控制器,所以其参数对仿真结果的影响很大。不同电流控制算法下系统模型是不同的,因此各种算法下控制器参数一般也不同,那么就很难区别仿真结果中的差异是由于控制参数造成的,还是由于不同的电流控制方法造成的。永磁同步电机电流控制算法仿真模型如图2所示。

图2 永磁同步电机电流控制算法仿真模型Fig.2 Simulation model of current control method for permanent magnet synchronous motor

本文利用电机的数学模型自行构造永磁同步电机仿真模块,再根据前述各电流控制算法推导出的电流相角关系构造d轴和q轴电流分量计算模块[8,17-18],利用各变量之间的数学关系计算输出转矩、电机端电压、功率因数、去磁因数和电机效率。从而避免了控制器参数对仿真结果的影响,也避免了复杂的控制器参数整定和坐标变换。

5 仿真结果分析

仿真采用了1台额定转矩为12 N◦m的凸极永磁同步电机,电机的参数为额定转矩 Te=12 N◦m,额定转速 ω=2 000 r/min,极对数 p=4,电枢电阻Rs=0.98 Ω,永磁磁场 Ψf=0.26 V◦s,d轴电感Ld=0.009 H,q轴电感Lq=0.036 H。仿真系统在下面2种不同情况下,用4种不同的电流控制算法对实验电机的电磁转矩Te,电机端电压 us,功率因数 cos φ,去磁因数 ξ,电机效率 η进行了深入研究。仿真图如图3所示。

5.1 转速不变,负载增大

图3为仿真中保持转速给定1 000 r/min不变,电枢电流从零开始增大,模拟转速不变,负载增大的运行情况。

由图3可见,随着电枢电流的增加,在id=0控制中,输出转矩和电流呈线性正比关系,因而容易获得高质量的转矩控制特性;电机端电压和电枢电流也呈线性正比关系,并且是4种控制方法中增加最快的,因此这种控制方法对器件耐压和容量的要求较高;电机功率因数下降最快,而且在整个运行范围内其功率因数几乎都是4种方法中最低的,因此逆变器容量的利用率较低;电机效率的下降也比较快,基本和恒磁链控制类似;由于d轴电流分量为零,不存在d轴电枢反应,因此去磁因数为零,不必考虑去磁问题,可以降低对永磁材料的要求。

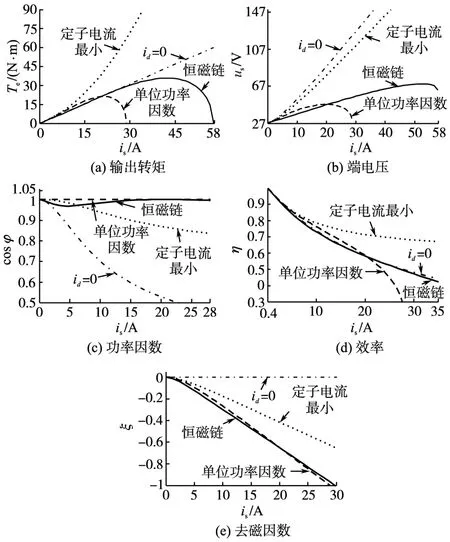
图3 n=1 000 r/min 时电机 Te,us,cos φ,η,ξ曲线Fig.3 Te,us,cos φ,η,ξ curves of motor when n=1 000 r/min

在定子电流最小控制中,随着电枢电流的增加,输出转矩是4种方法中增加最快的,但转矩和电流成非线性关系,因而容易获得较高的转矩,但转矩的控制却比id=0控制要复杂;电机端电压增加也比较快,和电枢电流呈线性关系,增加速度仅次于id=0控制,因此对逆变器耐压的要求也比较高;电机功率因数下降比id=0控制有很大改善;电机的效率随电枢电流的增加也呈下降趋势,但与其它3种方式相比却是最高的;由于d轴电流分量不为零,存在d轴电枢反应,随电枢电流的增加去磁因数增大较快,但小于单位功率因数控制和恒磁链控制。

在单位功率因数控制中,随着电枢电流的增加,输出转矩增加,但很快出现极值,比较小的极值严重影响了转矩的输出,并且转矩和电流成非线性关系;电机端电压增加比较慢,降低了对逆变器耐压的要求;在整个输出范围内,电机功率因数始终保持为1不变,提高了逆变器容量的利用率;在负载较小时,电机的效率随电枢电流的增加呈下降趋势,和id=0、恒磁链控制类似,但在大负载时其下降的速度很快,比其它3种方式效率都低;由于d轴电流分量不为零,存在 d轴电枢反应,随电枢电流的增加去磁因数增大较快,和恒磁链控制类似。

在恒磁链控制中,轻载时输出转矩和电流近似呈线性正比关系,但随着电枢电流的增加,近似的线性关系被破坏。转矩极值的出现也影响了转矩的输出,但其极值比单位功率因数控制时有很大提高,在本文仿真条件下其最大转矩约是单位功率因数控制最大转矩的1.7倍;电机端电压增加比较慢,而且基本和电流的增加呈线性关系,降低了对逆变器耐压的要求;除了在轻载时功率因数略低外,电机功率因数接近1,特别是重载时功率因数比较高,提高了逆变器的利用率,其功率因数特性在整个输出范围内都和单位功率因数控制类似;电机的效率随电枢电流的增加呈下降趋势,整个输出范围内都基本和id=0控制相类似,与定子电流最小控制相比效率较低;由于d轴电流分量不为零,存在d轴电枢反应,随电枢电流的增加去磁因数增大较快,其去磁因数随电流变化的特性在整个输出范围内都和单位功率因数控制类似。

5.2 负载不变,转速增大

图4为仿真中保持负载转矩给定12 N◦m额定值不变,转速从100 r/min升至 3000 r/min,模拟负载不变,转速增大的运行情况。由图4可见,随着转速的增加,4种控制方式下电机端电压和电枢电流均呈线性正比关系,id=0控制是4种控制方法中端电压增加最快的,而其他3种控制方式下端电压增加速度差别不大;id=0控制的电机功率因数下降最快,在整个范围内其功率因数都是4种方法中最低的,因此逆变器容量的利用率较低,但随着转速的增加,功率因数的下降逐渐放缓。单位功率因数控制下的功率因数当然在整个输出范围内保持为1不变,恒磁链控制功率因数与其差别不大,只是数值上略低;随着速度的增加,4种控制方式下电机的效率均增加,而且在低速时效率提高较快,高速时效率提高逐渐放缓。定子电流最小控制的效率最高,其次是单位功率因数控制,而id=0和恒磁链控制效率最低,且二者差别极小;随着速度的增加,4种控制方法去磁因数均保持为常数不变,id=0控制由于d轴电流分量为零,不存在d轴电枢反应,因此去磁因数为零。恒磁链控制去磁因数最大,而定子电流最小控制和单位功率因数控制处于二者之间。

6 结论

id=0控制,最大优点是d轴电流为零,电枢电流无去磁作用,因此不必考虑永磁体去磁带来的一系列问题;另外电机输出转矩和定子电流幅值成线性关系,其控制特性和直流电机非常相似,容易获得高精度的转矩控制特性;但这种控制方式下电机端电压升高和功率因数下降都是4种方式中最快的,电机和逆变器的容量不能得到充分利用,对功率器件耐压要求也比较高;同时电机磁阻转矩没有得到利用,影响了转矩的输出能力,总体的运行效率也比较低。因此这种电流控制方法比较适合于中小功率的高性能伺服系统,如机床伺服控制、机器人运动控制等,由于系统结构比较简单,在工程中得到了广泛的应用。

定子电流最小控制,虽然其转矩和定子电流不是线性关系,但在转矩一定时,定子电流最小,有利于减小铜损;相对于id=0控制功率因数有较大提高,对逆变器的容量要求有所降低,电机运行效率也比较高;但随着负载的增大,电机端电压升高速度和去磁因数增大速度均比较快,功率因数也有所下降;总体来看,这是一种比较优越的控制方法,但由于计算量比较大,因此应用受到限制,主要用于要求高转矩的领域,比如电动车辆的启动阶段。

单位功率因数控制,在整个工作区间内功率因数保持为1;随着定子电流的增大,初期电机端电压增大较慢,后期还有所降低,对功率器件耐压要求较低;但其最大的缺点是转矩的极大值太小,因而其输出力矩比较小,并且其转矩和电流不是线性关系;效率下降和去磁因数增大也比较快。和恒磁链控制相比,除最大输出转矩较小外,其余各项性能比较接近,由于其性能的局限性,其工程应用还很罕见。

恒磁链控制,转矩和电流也不是线性关系,且有最大值限制,但其最大转矩比单位功率因数控制最大转矩大得多,且线性区域也有所扩大;电机端电压、功率因数、效率、去磁因数特性均和单位功率因数控制差别不大。这种控制方法的应用领域和id=0控制类似,而且很大程度上解决了端电压升高和功率因数降低的问题,因而在高速、大容量应用领域具有一定的应用前景,比如高速机床的主轴和伺服系统。

[1]Schiferl R F,Lipo T A.Power Capability of Salient Pole Permanent Magnet Synchronous Motors in Variable Speed Drive Applications[J].IEEE Transactions on Industry Application,1990,26(1):115-123.

[2]李崇坚.交流同步电机调速系统[M].北京:科学出版社,2006.

[3]陈伯时.电力拖动自动控制系统—— 运动控制系统[M].北京:机械工业出版社,2004.

[4]Bose B K.A High-performance Inverter-fed Drive System of an Interio r Permanent Magnet Syschronous Motor for Adjustable Speed Drives[J].IEEE T ransactions on Industry Application,1988,24(6):987-997.

[5]曾朝晖,陈志杰.内永磁同步电机的电流控制策略[J].电气传动,1996,26(2):11-16.

[6]陈荣.永磁同步电机控制系统[M].北京:中国水利水电出版社,2009.

[7]王成元,夏加宽,杨俊友,等.电机现代控制技术[M].北京:机械工业出版社,2006.

[8]Morimoto S,Takeda Y,Hirasa T.Current Phase Control Methods for Permanent Magnet Synchronous Motors[J].IEEE Transactions on Power Electron.,1990,5(2):133-139.

[9]BK.BOSE.现代电力电子学与交流传动[M].王聪,译.北京:机械工业出版社,2006.

[10]李长红,陈明俊,吴小役.PMSM调速系统中最大转矩电流比控制方法的研究[J].中国电机工程学报,2005,25(21):169-174.

[11]Jahns T M,Kliman G B,Neumann T W.Interior Permanent Magnet Synchronous Motor for Adjustable Speed Drives[J].IEEE on Industry Application,1986,22(4):738-747.

[12]Tursini Marco,Parasiliti F rancesco,Zhang Daqing.Realtime Gain Tuning of PI Controllers for Hig h-performance PMSM Drives[J].IEEE Transactions on Industry Applications,2002,38(4):1018-1026.

[13]王江,王静,费向阳.永磁同步电机的非线性 PI速度控制[J].中国电机工程学报,2005,25(7):125-130.

[14]杨明,牛里,王宏佳,等.PMSM矢量控制系统的精确仿真研究[J].电气传动,2009,39(10):14-17,66.

[15]高延荣,舒志兵,耿宏涛.基于Matlab/Simulink的永磁同步电机矢量控制仿真[J].机床与液压,2008,36(7):296-299.

[16]冯晓艳,范红刚.PMSM伺服系统的控制[J].电机与控制学报,2007,11(3):244-247.

[17]Morimoto S,Takeda Y,Hirasa T.Servo Drive System and Control Characteristics of Salient Pole Permanent M agnet Synchronous M otor[J].IEEE Transactions on Industry Applications,1993,29(2):338-343.

[18]M orimoto S,T akeda Y,Hatanaka K,et al.Design and Control Sy stem of Inverter Driven Permanent Magnet Synchronous Motors for High T orque Operation[J].IEEE Transactions on Industry Applications,1993,29(6):1150-1155.