用于水中兵器电磁消涡技术的机理研究

张 辉，范宝春，周本谋，陈志华

（南京理工大学 瞬态物理国家重点实验室，南京210094）

用于水中兵器电磁消涡技术的机理研究

张 辉，范宝春，周本谋，陈志华

（南京理工大学 瞬态物理国家重点实验室，南京210094）

电磁场在导电的流体中产生的Lorentz力可以有效地改变流体边界层的结构，从而实现对流场的控制。基于电磁场和Lorentz力的基本方程，对由电极和磁极按一定规律排列形成的平板和圆柱状物体的电磁场空间分布，以及将其置于流动的弱电介质溶液时所形成的Lorentz力的空间分布进行了数值研究，并对Lorentz力的衰减规律、渗透深度和脉动程度进行了讨论。根据Lorentz力的数值结果，还对电磁场中的流动现象进行了数值计算，揭示了Lorentz力对圆柱绕流的控制过程。

电磁场；Lorentz力；流体控制；圆柱绕流

1 引 言

粘性流体在运动物体表面形成的边界层可使该物体减速，甚至产生噪音、振动和失稳，有时还会造成物体的变形和损坏，这往往不是人们所期望的，而这些现象通常可以通过流体边界层的控制加以抑制。因此，动力推进的物体，通过对其表面边界层的有效控制，可以提高推进效率、增加运动的稳定性和减少燃料损耗，减小航迹范围，减小震动与噪声，增强隐蔽性，这些对改进舰船、潜艇或水下航行器的性能是非常有价值的。

20世纪60年代，Gailitis[1]设计了一种条状电极和磁极交错布置的电磁激活板，将其浸入流动的弱电介质时，由于电磁场的作用，流体的边界层受到方向一致的Lorentz的作用，从而改变了流体边界层的结构。Weier[2]将此类激活板包覆在圆柱两侧，对由此形成的受控绕流进行了实验研究和数值计算。Kim等人[3]对于处在连续电磁力和脉冲变化的电磁力作用下的圆柱绕流进行了实验研究，并研究了在这些情况下升力和阻力变化。本文作者[4-6]也对圆柱绕流的电磁控制做了大量研究。但迄今，在相关的数值研究中用于平板或圆柱状电磁激活板的电磁力分布大都采用近似公式，它不仅不能讨论Lorentz力的分布和各因素的影响，在不同情况下其参数的选取也比较困难。

本文通过数值计算，求解分布于平板或圆柱电磁激活板周围的Lorentz力场，并对其分布、衰减规律、渗透深度和脉动程度进行了讨论。根据Lorentz力的数值结果，本文还以圆柱电磁激活板为例，对电磁场中的流动现象进行了数值计算，其结果与实验现象一致，揭示了Lorentz力对圆柱绕流的控制过程。

2 控制方程

2.1 电磁场方程

电极和磁极条相间排列组成的平板和圆柱电磁激活板置于导电流体中，分别如图1和图2所示。由右手定则可知，由此产生的电磁力（Lorentz力）与流体的流动方向相同，从而使边界层附近的流体加速，流体分离点后移直至消除，这无疑可以改变平板和圆柱流体边界层的结构，从而实现对流场的控制。

Lorentz力的表达式为

其中J是电流强度，B是磁感应强度。由欧姆定律，电流强度

其中，σ为流场电导率，E为电场强度矢量，U为流动速度矢量。

对于弱导电介质，σ （U×B） 相对于σE很小，可忽略不计，因此

电磁场的Maxwell方程

其中，μ0是磁导率，ε0是介电常数，ρe是电荷密度。

本文仅讨论对电极施以恒定电压，磁极采用永久磁铁，并置于弱导电、弱导磁和电中性介质中的情形，此时，可以忽略诱导电场和诱导磁场[7-8],所以

进而有Laplace方程

其中，φ是电势（或磁势），E=-▽φ或B=▽φ。

图3 电极间的匀强电场Fig.3 The equality electric field between the electrode

其边界条件

磁场有同样的方程。

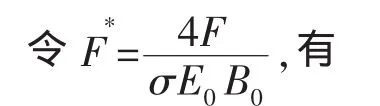
此时，Lorentz力场在流场空间是独立于流动，且不随时间变化的恒定力场。

2.2 流动方程

描述电磁力控制弱电介质溶液中流动的无量纲形式的守恒方程可以写为：

对于电磁场中的圆柱绕流，低雷诺数情况下，采用二维近似，利用指数极坐标（ξ,η ），即 r=e2πξ和θ=2πη，于是流函数ψ定义为

其中，ur和 uθ为速度 V 在 r，θ方向的分量，H=4π2e2πξ。 涡量定义为

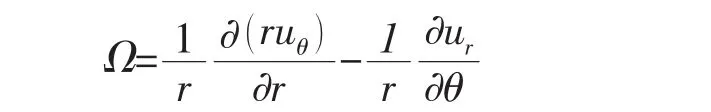
此时，守恒方程写作：

考虑到圆柱壁面无滑移，并设圆柱外的初始流场无旋，于是

2.3 数值计算

平板电磁场，（7）式写成

通过二阶差分求解，可求得电场强度矢量E和磁感应强度矢量B的空间分布。进而利用（9）式，得到Lorentz力的空间分布。由于该力场是独立于流动的恒定场，故方程（11）右端的Lorentz力项为常数项，其余各项构成标准的粘性流动的N-S方程，因此可以利用常用的N-S方程的数值方法来求解。

基于此，方程（11）采用 ADI格式（alternative-direction implicit）

圆柱电磁场，在柱坐标中，（7）式写成

上述格式具有时间一阶精度和空间二阶精度，详见文献[4]。计算时，圆柱表面采用无滑移边界，离圆柱无穷远处的流体为势流流动。

方程（12）采用 FFT 格式（fast Fourier transforms）

3 结果讨论

3.1 Lorentz力的分布

计算得到的平板和圆柱表面的Lorentz力在表面法向（y）与展向（x）的空间分布分别如图4（a），4（b）所示，z轴代表Lorentz的大小（为突出立体图像，曲面上用条纹表示等值区域）。由图可见，由于电磁激活板的电极和磁极的交错排列，Lorentz力沿展向（x）呈周期分布，其周期长度与激活板电极（或磁极）宽度以及间距有关，在电极与磁极板交界处取极大值，此后递减，在各电极与磁极板的中央位置取极小值；沿法向（y）则以指数规律迅速衰减。

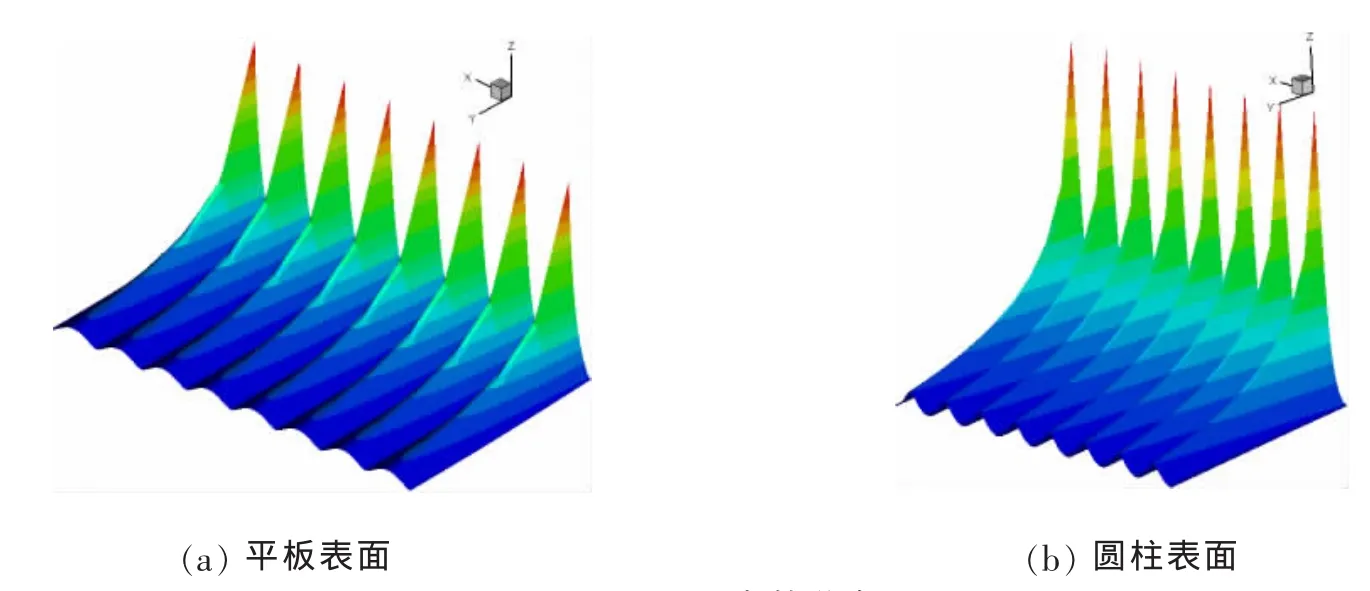
图4 Lorentz力的分布Fig.4 The distribution of Lorentz force

3.2 Lorentz力的渗透深度

为了方便计算和讨论，特别是，为了与近似公式（18）比较，将Lorentz力沿展向取平均值，从而得到展向平均Lorentz力在y方向的衰减曲线。图5中虚线和细实线分别是极板宽度d/a为0.03时，平板和圆柱表面的衰减曲线。由于两者结构不同，圆柱表面的电势和磁势衰减较快，即梯度较大，故其表面附近的电场强度和磁场强度都比较大，所以产生的Lorentz力也大，但随法向距离y的增加而很快衰减，故力场渗透深度较小。平板则相反，表面附近Lorentz力较小，但衰减较慢，渗透深度大。在现行的相关计算中，通常采用近似衰减公式[9]

图5 Lorentz力沿法向的分布Fig.5 The distribution of Lorentz force along the normal direction

其中α是可调参数。为了与对应于d/a=0.03的数值计算结果比较，选取适当的α，从而由该式得到圆柱情况下的Lorentz力衰减曲线，如图5中粗实线所示，它与数值计算曲线符合较好。

3.3 Lorentz力的脉动

Lorentz力与展向平均Lorentz力的差称为Lorentz力的脉动。该脉动值在法向（y）与展向（x）空间的分布如图6（a），6（b）所示,它们分别代表平板和圆柱，z轴代表Lorentz脉动的大小。Lorentz力的脉动也呈周期分布，在电极与磁极板交界处取极大值，此后递减，在各电极与磁极板的中央位置取极小值。并且，极板附近脉动量最大，随着（y）的增大，脉动量迅速减小，最后减小到0（即没有脉动），此时，Lorentz力也衰减为0。另外，从脉动图中可以看出，圆柱表面的脉动比平板表面稍大。

图6 Lorentz力的脉动Fig.6 The fluctuation of Lorentz force

3.4 Lorentz力对流动边界层的控制

本文仅讨论Lorentz力对圆柱绕流的控制。无量纲的圆柱半径为1，极板宽度为0.03，来流雷诺数Re为200。Lorentz力的分布由方程（14）求得。据此，再由方程（11）和（12）可求得电磁力作用下的圆柱绕流的流场。图7是根据计算结果（左）绘制的流场涡量分布图与实验结果（右）的比较。其中图7（a）为未加电磁力时，圆柱绕流的典型卡门涡街。图7（b）为施加电磁力后，流体的动量增加，分离点后移，开始消涡；图7（c）所示，在电磁力作用下，卡门涡街逐渐消失，消涡效果明显；图7（d）是消涡的最终结果。这表明电磁力有效地控制了边界层的流动，抑制了流体在圆柱表面的脱体和由此形成的涡街，从而可以大大改变圆柱表面的受力情形。计算结果反映的流场图像与实验结果相符。

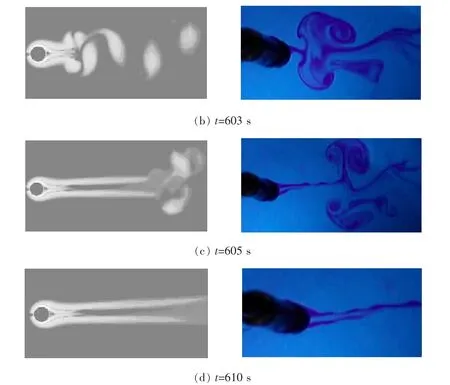
图7 Lorentz力作用下，圆柱绕流的数值计算（左）与实验结果（右）对比Fig.7 The results of numerical calculations and experiments with the application of Lorentz force

4 结 论

将电磁激活极置于流动的弱电介质溶液中，由此形成的Lorentz力可以对边界层和绕流实现有效控制。在相关计算中，Lorentz力通常采用近似公式，它不仅不能讨论Lorentz力的分布和各因素的影响，在不同情况下，其参数的选取也比较困难。本文根据基本方程，直接对电磁场、Lorentz力场和绕流进行了数值计算，结果表明：

（1）Lorentz力沿激活板法向（y），呈指数衰减，沿展向（x），呈脉动分布。在电极与磁极板交界处取极大值，在电极与磁极板的中央位置取极小值。

（2）圆柱表面附近的Lorentz力比平板的大但衰减较快，且圆柱表面Lorentz力的脉动幅度比平板大。

（3）在Lorentz力作用下，圆柱绕流的数值结果形像地描述了尾流涡街的抑制过程，与实验结果相符。

[1]Gailitis A,Lielausis O.On a possibility to reduce the hydrodynamical resistance of a plate in an electrolyte[J].Applied Magnetohydrodynamics,1961,12:143-146.

[2]Weier T,Gerbeth G,Mutschke G,et al.Experiments on cylinder wake stabilization in an electrolyte solution by means of electromagnetic forces localized on the cylinder surface[J].Experimental Thermal and Fluid Science,1998,16:84-91.

[3]Kim S J,Lee C M.Investigation of the flow around a circular cylinder under the influence of an electromagnetic field[J].Exp.Fluids,2000,28:252-260.

[4]陈志华,范宝春.包覆电磁场激活板的圆柱尾迹的数值研究[J].力学学报,2002,34(6):978-983.Chen Z H,Fan B C.Numerical investigation on wake of cylinder covered with electro-magnetic actuator[J].Acta Mechanica Sinica,2002,34(6):978-983

[5]范宝春,姜孝海,叶经方.电磁力的消涡与减阻[J].兵工学报,2003,24(1):74-77.Fan B C,Jiang X H,Ye J F.Vortex suppression and resistance reduction by magnetohydrodynamic force[J].Acta Armamentar,2003,24(1):74-77.

[6]Zhang H,Fan B C,Chen Z H,Dong G,Zhou B M.Open-loop and optimal control of cylinder wake via electro-magnetic fields[J].Chinese Science Bulletin,2008,53(19):2946-2952.

[7]Crawford C H,Kamiadakis G E.Reynolds stress analysis of EMHD controlled wall turbulence,Part I streamwise forcing[J].Phys.Fluids,1997,9:788-806.

[8]Berger T W,Kim J,Lee C.Turbulent boundary layer control utilizing the Lorentz force[J].Phys.Fluids,2000,12(3):631-649.

[9]Oliver P,Roger G.Electromagnetic control of seawater flow around circular cylinders[J].Eur.J Mech.B-Fluids,2001,20:255-274.

Mechanism investigation of vortex suppression by Lorentz force for underwater ordnance

ZHANG Hui,FAN Bao-chun,ZHOU Ben-mou,CHEN Zhi-hua

(National Key Laboratory of Transient Physics,Nanjing University of Science and Technology,Nanjing 210094,China)

The Lorentz forces generated by electromagnetic fields in the electrolyte solution may modify the structures of the flow boundary layer effectively and therefore it can be used to realize flow controls.Based on the equations of magnetic and electric fields and the formula of Lorentz force,the electromagnetic fields induced by an actuator with flat or cylindrical shape in a moving low-conducting electrolyte,consisting of a specific array of electrodes and permanent magnets were investigated numerically and the distributions of Lorentz forces were calculated also.According to the calculating results,the attenuation,effective depth and fluctuation of Lorentz force in the flow field were discussed.The numerical investigations on the wake of a cylinder covered with electro-magnetic actuators were performed and the evolutional processes of wake control by Lorentz forces were described.

electromagnetic field;Lorentz force;flow control;cylinder wake

O361

A

1007-7294（2011）11-1210-07

2011-05-08

张 辉（1981-），男，南京理工大学博士生，从事流体力学研究，E-mail:zhanghui1902@hotmail.com；

范宝春（1945-），男，教授，博导，从事流体力学研究，E-mail:bcfan@mail.njust.edu.cn。