船体阻力计算中模型常（系）数的敏感性研究

陈 康，黄德波，李云波

（1上海船舶研究设计院，上海 200032；2哈尔滨工程大学 船舶工程学院，哈尔滨 150001）

1 引 言

计算流体力学迄今已获得了很大的发展。在船舶工程领域，船舶性能预报、船型优化设计和对船体周围流动现象、机理的研究越来越多地受益于船舶CFD技术[1-5]。但是，由于船舶CFD技术仍处在发展阶段，它所能处理的流动问题和所能达到的精度依旧受其自身发展水平及硬件等因素的限制，这一特点在解决湍流流动问题时尤其突出。众所周知，以目前CFD的发展水平，采用不同湍流模型处理同一湍流问题时，很难得到较一致的数值解。尽管对于湍流问题的研究已经发展到了工程应用的阶段，并且形成了多种繁简不同的湍流封闭模型[6]，但众多的选择也恰恰表明了目前的湍流模型发展还不够完善，尤其是在船舶CFD研究中自由水面与湍流边界层相互作用问题仍未得到解决，使得目前处理船舶粘性绕流场问题的CFD技术中需要多种假设及存在不确定度[7]。在现阶段的船舶水动力性能研究中，一方面是没有一种能够完全被船舶CFD用户所认可的适用于船舶阻力性能研究的湍流模型；另一方面，在现有的各个湍流模型中或多或少存在一些模型常（系）数。这些湍流模型常（系）数有一定的取值范围，因而它们的推荐值是否适用于船舶阻力等水动力性能的研究还有待进一步探讨。

在以往工作的基础上，文中以提高船舶阻力数值计算的可靠性及可信度为目的，尝试修正两个经常用于工程计算的二方程湍流模型中的模型常（系）数，以观察这种修正对船舶阻力数值计算的影响，并确定在船舶阻力性能研究中各湍流模型常（系）数的适用性。

2 方程模型化的原则

在推导k和ε的微分输运方程过程中，引进了新的未知项，如ε输运方程中的扩散项、产生项和消耗项等。根据对湍流现象的了解以及建立封闭方程组的基本目的，有必要遵循一定的假设和原则，对这些未知项作合理的模化，即用流场中的已知量来替代未知量。方程模型化应该遵循的原则如下[8-9]：

（1）时均化的NS方程与脉动方程是模化的基本出发点，细致的湍流涡结构的影响在时均化时被略去；

（3）所有需要模化的项在模化后的形式必须与原项有相同的量纲；

（4）模化后的形式必须与原项有相同的数学特性，如对称性、不变性、置换性、迹为零等，并且与实验和观察结果相吻合；

（5）各湍流特征量的湍流扩散速度均假设与该量的梯度成正比；

（6）高雷诺数特性，即所有主要由大尺度涡决定的性质不受粘性影响，而小尺度涡结构在统计上则与平均运动和大尺度涡无关，是各向同性的。此假设适用于各种流动中，而十分邻近固壁的区域除外；

（7）湍流各种尺度或者可以用（k，ε）表示，或者可以用（ε，ν）表示，后者仅用于由小尺度涡决定的性质；

（8）湍流模型中的一些常（系）数均由实验来确定；

（9）可实现性。模化后的输运方程不应当产生在物理上不可能的值。这一原则虽然是理所当然应该满足的，但是在实际计算中还未被应用。

与初始方程相比，模化后的方程不存在封闭问题，但是描述流动问题的精度降低了。而且方程模型化过程中引入的模型常（系）数不是物性常数，它们与湍流流动状态有关，因此必须通过实验来确定。实际上，在早先确定各模型常（系）数的实验中，由于受到实验者、实验设备及实验方法等因素的影响，根据实验得到的这些模型常（系）数有一定的取值范围，这也从另一个侧面反映了湍流模型中存在的变数及不确定性，这种特性必然导致数值计算中与计算模型相关的模型误差及不确定度。将湍流模型理论应用于船体阻力性能研究中有必要对此展开探讨。

3 物理模型和控制方程[10-15]

文中模拟船体模型在静水中以定常速度U0作匀速直线运动时船体周围的粘性湍流场，并计算阻力值。根据相对运动原理，可视作船体模型静止，而水以速度-U0从远方相对于船体模型匀速流动。

假定流体不可压，流动定常，则流场的连续方程和雷诺方程分别为：

其中：ui，uj为时均速度分量 （i， j= 1，2，3）；P为压力时均值；ρ为流体密度；μ 为流体粘性系数；gi为重力加速度分量；ρu为雷诺应力项。

为了研究湍流模型及模型系数对船体阻力值计算的影响，文中选择了两种二方程湍流模型，即标准k-ε湍流模型和k-ω湍流模型。以下简单给出模化后的各湍流模型方程以及各个模型常（系）数的取值：

（1）k-ε二方程湍流模型

模型常（系）数取值范围为：Cμ=0.07～0.11，Cε1=1.41～1.45，Cε2=1.8～2.0，σk=0.8～1.3，σε=0.8～1.3。通常推荐采用的模型系数值为：Cμ=0.09，Cε1=1.44，Cε2=1.92，σk=1.0，σε=1.3。

（2）k-ω二方程湍流模型

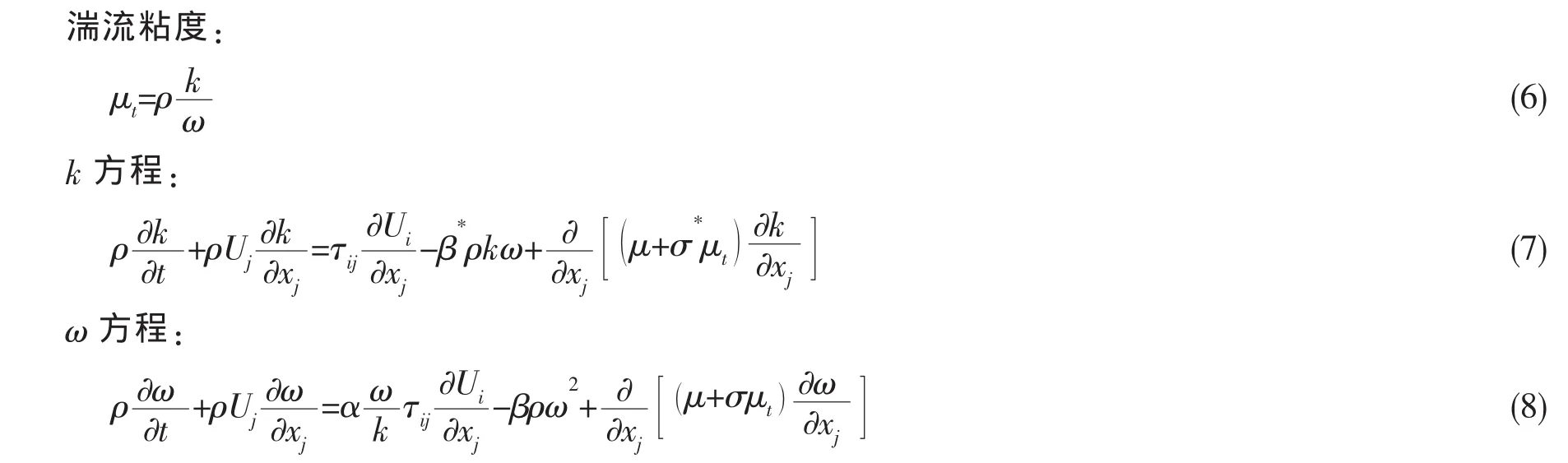
通常采用的模型系数推荐值为：β*=9/100，σ*=1/2，α=5/9，β=3/40，σ=1/2。

4 计算模型的建立与网格生成

4.1 Wigley船型

文中采用船型之一为Wigley船型，船长L=3.0 m，船宽B=0.3 m，船体Fr数为0.3。计算域尺寸为5.5L×1.5L×1.062 5L，坐标系原点位于舯横剖面底部。X轴指向船艏，Y轴指向左舷，Z轴竖直向上，建立计算域时考虑了对称性。由于Wigley船型简单，文中用六面体分块结构网格将计算域离散，静水面处、对称面上网格分布如图1所示，网格数为91×24×52=113 568。

图1 Wigley船计算模型静水面处、对称面上网格分布Fig.1 Grid distribution of Wigley model around still water plane and symmetry plane

4.2 数学三体船型

文中采用的另一船型为数学三体船型，中体船长为L=2.6 m，船宽为B=0.196 m。两个侧体的形状与尺寸均与中体相同。相对于中体，侧体在船长方向（X轴）向后偏移1.04 m，在船宽方向（Y轴）分别偏移0.52 m。船体Fr数为0.4。三体船型的计算域尺寸为5.5L×1.1L×0.525L，考虑了计算域的对称性。X轴指向船头，Y轴指向左舷，Z轴竖直向上。静水面处、对称面上网格分布如图2所示。网格数为109×43×42=196 854。

图2 数学三体船计算模型静水面处、对称面上网格分布Fig.2 Grid distribution of mathematical trimaran model around still water plane and symmetry plane

5 计算结果及验证分析

5.1 Wigley船型的阻力计算结果及分析

文中选取二方程湍流模型，并尝试变动模型常（系）数来数值求解Wigley船型的阻力，基于标准k-ε湍流模型和k-ω湍流模型的计算值分别由表1～5及表6～8给出。分析各表中的计算结果可以看出，在基于标准k-ε湍流模型的计算结果中：

（1）压阻力几乎不受 5个模型常（系）数取值变化的影响，总阻力的变化主要由摩擦阻力的变化而引起；

（2） 总阻力（摩擦阻力）随 Cμ、Cε2、σε取值的增大而增大。 在各常（系）数的取值范围内，Cμ使得总阻力有-2.22%～1.78%的变化（与采用推荐值得到的计算结果相比，下文类似），Cε2使得总阻力有-5.33%～2.89%的变化，σε使得总阻力有-7.11%～0%的变化；

（3）总阻力（摩擦阻力）随着Cε1取值的增大而减小。在其取值范围内，Cε1使得总阻力有1.11%～-0.44%的变化；

（4）σk的取值变化对各阻力分量无影响。

在选择k-ω湍流模型计算Wigley船型的阻力时，则能看出：

（1）压阻力几乎不受 3个模型常（系）数取值变化的影响，总阻力的变化主要由摩擦阻力的变化而引起；

（2）总阻力（摩擦阻力）分别随着β*或α取值的增大而减小。常（系）数取值变化±5%时，β*使得总阻力有1.28%～-1.49%的变化，α使得总阻力有1.07%～-1.28%的变化；

（3）总阻力（摩擦阻力）随β取值的增大而增大。β取值变化±5%使得总阻力有-1.92%～-1.49%的变化。

表1 模型系数Cμ的变化对Wigley船型阻力系数（×10-3）的影响Tab.1 Effect of modification of Cμon resistance coefficients （×10-3） of Wigley hull

表2 模型系数Cε1的变化对Wigley船型阻力系数（×10-3）的影响 Tab.2 Effect of modification of Cε1on resistance coefficients （×10-3） of Wigley hull

表3 模型系数Cε2的变化对Wigley船型阻力系数（×10-3）的影响Tab.3 Effect of modification of Cε2on resistance coefficients （×10-3） of Wigley hull

表4 模型系数σk的变化对Wigley船型阻力系数（×10-3）的影响Tab.4 Effect of modification of σkon resistance coefficients （×10-3） of Wigley hull

表5 模型系数σε的变化对Wigley船型阻力系数（×10-3）的影响Tab.5 Effect of modification of σεon resistance coefficients （×10-3） of Wigley hull

表6 模型系数β*的变化对Wigley船型阻力系数（×10-3）的影响Tab.6 Effect of modification of β*on resistance coefficients （×10-3） of Wigley hull

表7 模型系数α的变化对Wigley船型阻力系数（×10-3）的影响Tab.7 Effect of modification of α on resistance coefficients （×10-3） of Wigley hull

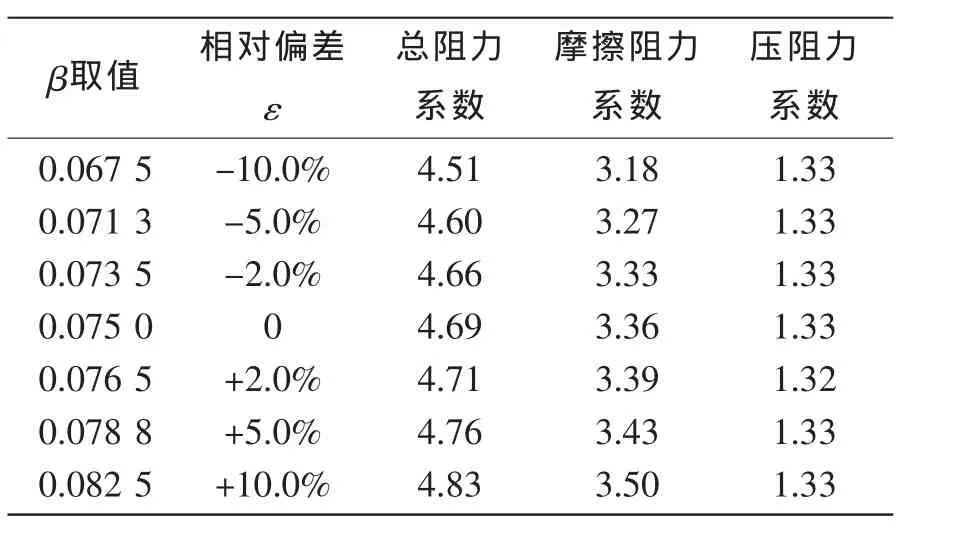
表8 模型系数β的变化对Wigley船型阻力系数（×10-3）的影响Tab.8 Effect of modification of β on resistance coefficients （×10-3） of Wigley hull

5.2 数学三体船型的验证结果及分析

文中计算了数学三体船型的阻力值来验证基于Wigley船型得到的结论。基于标准k-ε湍流模型和k-ω湍流模型的计算结果分别由表9～13及表14～16给出。

表9 模型系数Cμ的变化对数学三体船型阻力系数（×10-3）的影响Tab.9 Effect of modification of Cμon mathematical trimaran resistance coefficients （×10-3）

表10 模型系数Cε1的变化对数学三体船型阻力系数（×10-3）的影响Tab.10 Effect of modification of Cε1on mathematical trimaran resistance coefficients （×10-3）

表11 模型系数Cε2的变化对数学三体船型阻力系数（×10-3）的影响Tab.11 Effect of modification of Cε2on mathematical trimaran resistance coefficients （×10-3）

表12 模型系数σk的变化对数学三体船型阻力系数（×10-3）的影响 Tab.12 Effect of modification of σkon mathematical trimaran resistance coefficients （×10-3）

表13 模型系数σε的变化对数学三体船型阻力系数（×10-3）的影响Tab.13 Effect of modification of σε on mathematical trimaran resistance coefficients （×10-3）

表14 模型系数β*的变化对数学三体船型阻力系数（×10-3）的影响Tab.14 Effect of modification of β*on mathematical trimaran resistance coefficients （×10-3）

表15 模型系数α的变化对数学三体船型阻力系数（×10-3）的影响Tab.15 Effect of modification of α on mathematical trimaran resistance coefficients （×10-3）

表16 模型系数β的变化对数学三体船型阻力系数（×10-3）的影响Tab.16 Effect of modification of β on mathematical trimaran resistance coefficients （×10-3）

通过比较计算结果可以看出，尽管三体船型与Wigley船型在构型方面有很大的差异，但是两种船型的阻力值对湍流模型常（系）数的敏感性表现相一致；随着标准k-ε湍流模型中5个常（系）数分别在其取值范围内变化，船体总阻力值的变化幅度各不相同，其中σk引起的总阻力变化完全可忽略，σε引起的总阻力变化幅度最大（>5%），而 Cε1，Cμ和 Cε2三者的影响则介于 σk和 σε两者之间（1%～3%）；k-ω湍流模型中3个常（系）数的取值分别变化±5%时，三体船总阻力值的变化幅度介于1%～2%之间；船体压阻力计算结果对文中涉及的湍流模型常（系）数均不敏感，两个湍流模型中常（系）数的推荐值对船体压阻力计算有鲁棒特性。

6 结 语

文中选择两个典型的二方程湍流模型作为研究对象，通过变动其模型常（系）数来考察这种改变对船舶阻力数值计算的影响，并得出了一些有意义的结论。这些结论不仅有助于理解文中涉及的湍流模型及其模型系数在船舶阻力性能研究中的适用性，而且有助于理解数值计算中湍流模型导致的误差和不确定因素，对于开展CFD V&V（Verification and Validation）的研究工作也有积极意义。

[1]Zhang Zhirong,Zhao Feng,Li Baiqi.Numerical calculation of viscous free-surface flow about ship hull[J].Journal of Ship Mechanics,2002,6(6):10-17.

[2]张志荣,赵峰,李百齐.k-ω湍流模式在船舶粘性流场计算中的应用[J].船舶力学,2003,7(1):33-37.

[3]Chang Huaixin,Liu Yingzhong,Miao Guoping.Numerical simulation of three-dimensional viscous flow with free surface about a ship[J].Journal of Ship Mechanics,2003,7(3):33-39.

[4]赵 峰,李胜忠,杨 磊,刘 卉.基于CFD的船型优化设计研究进展综述[J].船舶力学,2010,14(7):812-821.

[5]陈 康,黄德波.CFD技术在三体船阻力性能研究中的应用[J].哈尔滨工程大学学报,2006(3):362-366.

[6]马 峥,黄少锋,朱德祥.湍流模型在船舶计算流体力学中的适用性研究[J].水动力学研究与进展,2009(2):207-216.

[7]张 楠,沈泓萃,姚惠之.阻力和流场的CFD不确定度分析探讨[J].船舶力学,2008,12(2):211-224.

[8]是勋刚.湍流[M].天津:天津大学出版社,1994.

[9]陈景仁.湍流模型及有限分析法[M].上海:上海交通大学出版社,1989.

[10]Wilcox D C.Turbulence modeling for CFD[M].California:DCW Industries,1994.

[11]Pieter Welleling.Principles of computational fluid dynamics[M].Berlin:Springer,2001.

[12]Versteeg H K,Malalasekra W.An introduction to computational fluid dynamics:The finite volume method[M].Essex:Longman Group Ltd,1995.

[13]陶文铨.数值传热学[M].西安:西安交通大学出版社,2001.

[14]王福军.计算流体动力学分析—CFD软件原理与应用[M].北京:清华大学出版社,2004.

[15]张兆顺,崔桂香,许春晓.湍流理论与模拟[M].北京:清华大学出版社,2005.