水池摇板式造波机传递函数研究

2011-06-07郑文涛姚木林

船舶力学 2011年11期

郑文涛，姚木林，兰波，张波

（中国船舶科学研究中心，江苏无锡 214082）

1 引言

2 造波机简介

拖曳水池造波系统由机械系统、电控系统和软件系统组成，图1所示为造波机摇板以及电动缸照片。其中，机械系统主要用于提供安装支撑以及推动池水运动以产生波浪，它包括18块摇板以及相应的支撑结构，造波板设计板宽为0.41 m，板高为2.1 m，板的浸深为1.6 m。电控系统包括控制计算机、多轴运动控制器、电机驱动器、交流伺服电机、电动缸、电控柜以及相关的辅助线路等，其作用是按照给定的运动条件驱动电动缸运动，从而驱动摇板运动。电控系统中控制器采用高性能奔腾CPU硬件平台，VxWork实时操作系统管理运动，并采用成熟的运动控制同步总线SERCOS-II用于同步控制，可在4 ms之内完全刷新99个伺服控制器的运动信息。软件系统由造波计算程序、操作服务程序和伺服控制程序三部分组成。其中造波计算程序主要完成各种类型波浪的离散化数据生成；伺服控制程序负责完成离散化数据的运动曲线的拟合，并驱动摇板以往复运动的形式描述出来；操作服务程序提供造波操作界面，负责调用造波计算程序，实现人机交互，完成上位计算机与控制器的通讯。

图1 造波机摇板及电动缸Fig.1 Segments and electric cylinders of wavemaker

3 传递函数理论计算方法

为了与试验得到的传递函数进行对比，本文首先对造波机传递函数的势流理论计算方法进行介绍。设水池为半无限长（或端部具有完全消波功能装置的有限长度），如图2所示，现考查理想不可压缩流体的二维运动。假设摇板作微幅摆动而且流体的运动是无旋的，则水池中波浪的运动可以用流场中的速度势Φ（ x,y,t）来描述。

图中造波板运动位置可以描述为：

其中，X0（t）为水面处板的运动位置，f（y）用于描述造波机的形式（推板或摇板）：

图2 造波运动示意图Fig.2 Sketch of segment movement

其中，h为水深，d为板浸深，参数σ表示造波形式，当σ=0时为推板式造波机，当σ=1时为摇板式造波机。

设摇板作如下周期性摇摆：

式中，Xa为摇板在水面处摆动的摆幅，ω为摇板摆动的圆频率。

基于势流理论，假设摇板作微幅摆动，并选取线性边界条件，则流体速度势Φ （x,y,t）应满足下列控制方程：

2.1.2 量表的重测信度选取20例夜尿症患者于2周后进行重复测量，三部分的重测信度系数分别为0.743、0.786和0.725(P<0.05)。

设摇板作如下周期性摇摆：

当x→∝,Φ→沿x正方向传播的进行波(8)

满足上述边值问题的一阶解析解可表示为：

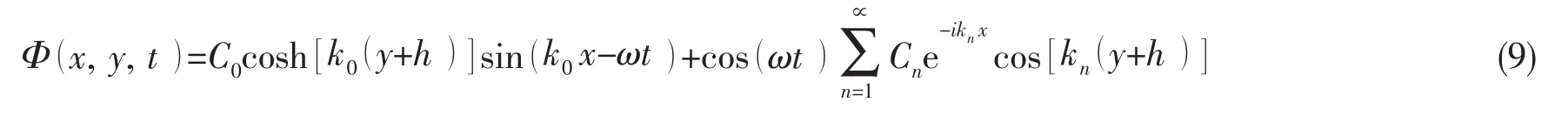
其中，参数k0和kn分别满足如下公式：2

造波板前的波面位移η为

当远离造波板时驻波成分将消失，并只保留第一项的进行波，此时波面高度也可表示为波高的形式：

其中波高H为

取摇板冲程S0=2Xa，则造波机波高和冲程的比值为

对于摇板式造波机σ=1，则波高和冲程的比值为

对于本造波机，设计水深为h=7 m，摇板浸深d=1.6 m，则可由上式计算得到本造波机的理论传递函数 R0。

4 水池传递函数试验

测试中采用的水池坐标系为如图3所示的右手直角坐标系，其中：X轴沿水池长边平行方向；Y轴沿造波机直立状态的板面方向；Z轴竖直向上。

波浪测试时，在水池中轴线上（即图3中a点）距离造波板50 m处安装一浪高仪，浪高仪安装如图4所示。本次测试采用的浪高仪型号为LGY-1A型，量程为600 mm，精度为1%，浪高仪经标定合格后使用。试验前测量造波板浸深为1.583 m。通过造波、采集波浪数据，并用波浪分析程序对波浪时历进行分析，得到统计结果。

本次试验选取波浪频率为0.2～2.0 Hz的正向规则波，频率间隔0.1 Hz，选取的目标波高约为造波机最大造波能力的50%，试验工况如表1所示。

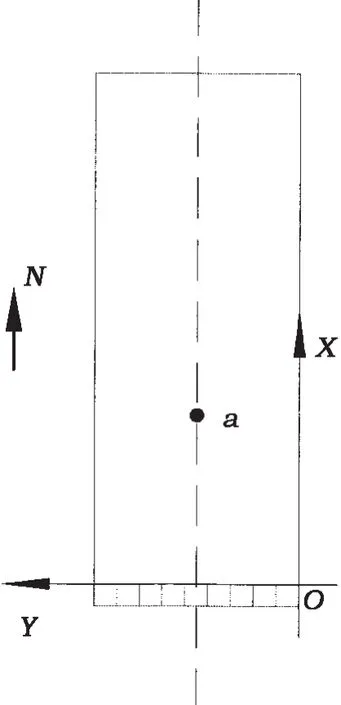
图3 水池坐标系示意图Fig.3 Tank coordinate system

图4 浪高仪安装图Fig.4 Arrangement of wave gauge

表1 传递函数测试工况表Tab.1 Test conditions of wavemaker transfer function

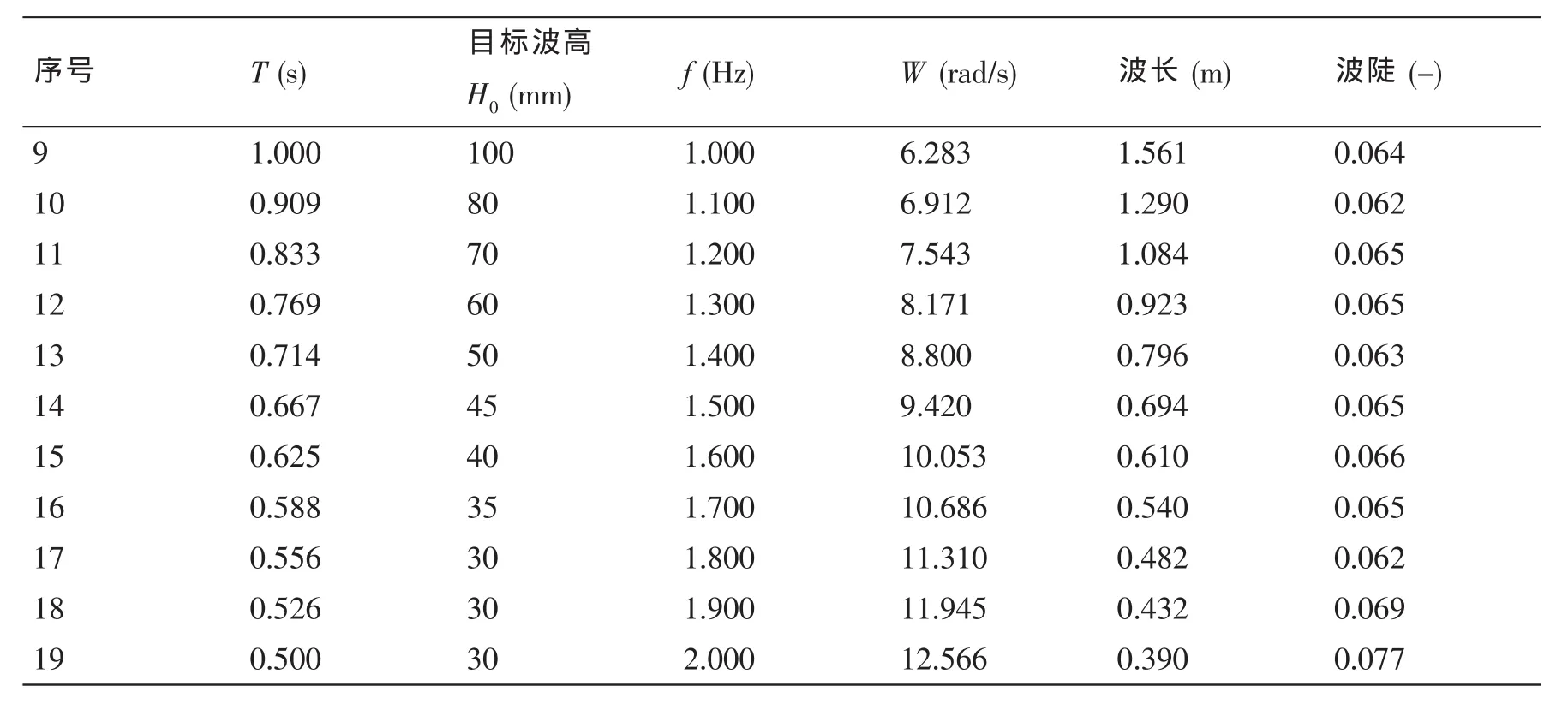
续表1

5 结果分析

通过测试、分析，得到实测波高Hm；再根据电动缸的运动幅值，可以得到设计水线处的摇板运动幅值Xa，进而可求得造波机的传递函数R′=Hm/2Xa。由于实测板的浸深为1.583 m，较设计浸深1.6 m小，故还需对计算得到的传递函数进行水浸深修正，得到设计水线处的传递函数R，本文采用线性修正的方法对水浸深进行了修正，计算得到的造波机传递函数如表2所示。由表2可知，频率较低时，造波机传递函数较小，制造单位波高所需的摇板板幅较大。

图5为实测传递函数R与理论传递函数R0的对比图，从图中可以看出，大部分频率下实测传递函数R约为理论值的95%；当频率为1.2～1.6 Hz时，实测传递函数较理论值95%略大；而当频率大于1.8 Hz时，R较0.95R0偏小，这一方面是因为短波在水池中消散较快，另一方面可能是因为频率较高时，系统响应能力较目标值偏弱。由实测传递函数与理论传递函数的对比结果可知，本造波系统具有良好的频响特性。

由对比结果可知，一般情况下，造波机实际冲程应按理论冲程增加5%才能制造出要求的波高。由于本次测试采用的波高并不是造波机的最大波高，根据造波机的一般特性，当波高增大时，系统传递函数会有一定的减小，因此，在进行造波机初步设计时，造波机的最大冲程应按理论冲程取大于5%的余量。