制导炮弹滚转控制系统设计

张 龙，吴小役，胡江峰 ，赵志勤

（西北机电工程研究所，陕西 咸阳 712099）

采用气动方式控制的制导炮弹一般布局为尾翼稳定，鸭舵控制形式，通过鸭舵控制可以实现制导弹的有控飞行，有效提高了射击精度，同时可以在一定程度上增加炮弹射程。制导控制可以通过滚转控制或非滚转控制的方式来实现。采用非滚转控制方案，可以解决滚转控制方案中控制力方向不够准确和制导精度有限的问题。为了简化结构，不在尾翼上安装执行机构，因此，采用非滚转控制方案的制导炮弹需要通过鸭舵实现对滚转的控制，为了消除鸭舵下洗在尾翼上产生的附加滚转力矩，一般采用自旋尾翼的设计方案［1］。

基于自旋尾翼式制导炮弹滚转控制，需要对制导炮弹全弹道上的滚转特性进行分析，确定合适的滚转控制模型，为制导炮弹的滚转控制系统设计提供依据。

1 运动模型建立

1.1 倾斜运动模型

基于小扰动假设［2］建立运动模型的线性化系统，建立描述制导弹侧向运动的扰动运动方程为：

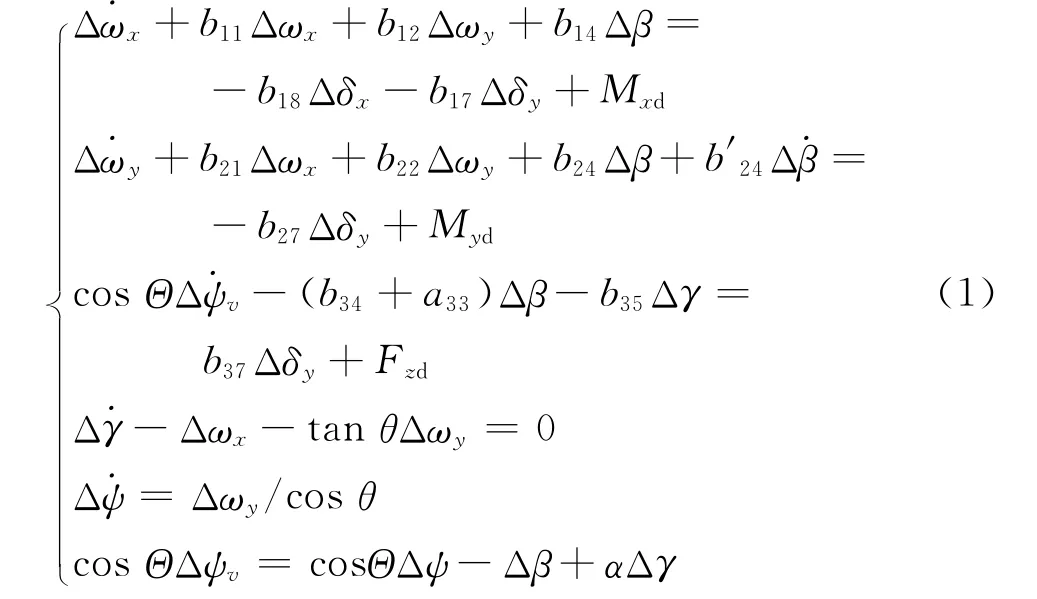
式中，Θ表示弹道倾角；θ表示弹体俯仰角；其他符号含义见文献［3］。

制导炮弹在控制飞行过程中，根据轴对称弹箭特性简化侧向扰动运动方程，分解出偏航扰动运动和滚转扰动运动方程。对公式（1）去掉小量乘积和分解方程处理，可得滚转运动的扰动方程为：

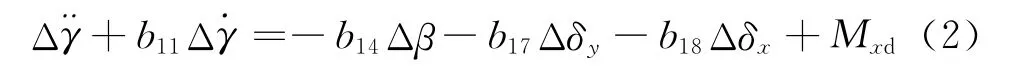
由于b14Δβ、b17Δδy两项主要为侧向扰动对滚转运动的影响，在分析滚转运动时可简化侧向扰动对滚转运动的耦合作用，得滚转扰动方程为：

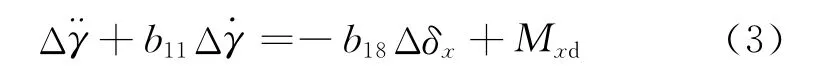
式中，Mxd表示作用于弹体上的经常干扰力矩，同时在偶然干扰作用下弹体还有瞬时的起始滚转角Δγ0和角速率Δ˙γ0。

1.2 滚转稳定回路模型

采用鸭舵偏转控制可以消除滚转运动中的经常和偶然干扰的影响。当弹体正向滚转时，鸭舵正偏产生负的横向操纵力矩，纠正弹体的正向滚转，反之弹体反向滚转，鸭舵负偏，消除弹体的反向滚转［4］。上述鸭舵的偏转控制通过滚转自动驾驶仪来实现。

如图1所示，滚转运动自动驾驶仪由传感器、控制器和舵面3部分组成，姿态传感器测量滚转位置偏差，控制器对偏差量进行运算得出舵面偏转角度，相应的舵面偏转可以实现对弹体的滚转稳定。其中，导弹滚转运动的传递函数可由式（3）经拉氏变换得到：

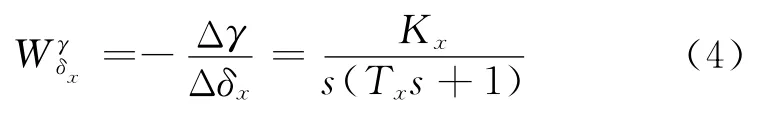
式中：Kx为导弹滚转运动传递系数；Tx为导弹滚转运动时间常数；Kx＝－b18／b11，Tx＝1／b11。该式为滚转运动对舵偏角的传递函数，而滚转运动对干扰力矩的传递函数可用等效舵偏角的形式采取与（4）式一致的传递函数。

干扰力矩的等效舵偏角表达式为：

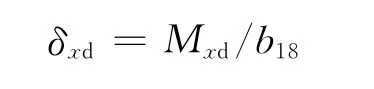
滚转控制中舵偏角调节规律设计为：

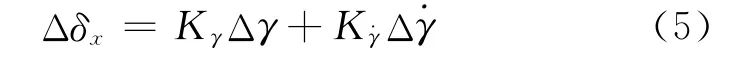
式（5）为滚转控制的PD控制器模型。

2 滚转稳定特性分析

将式（5）代入式（3）可得滚转运动自动驾驶仪作用下的运动：

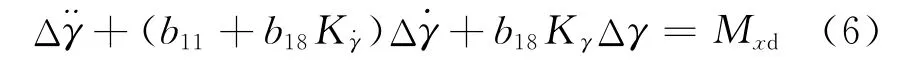
当系数Kγ、K˙γ大于0时，与式（3）相比，式（6）方程左边的系数增大，增加了b18KγΔγ，这一项的存在表示舵偏角随滚转角变化而偏转，产生于滚转方向相反的操纵力矩，消除弹体滚转角。同时滚转角速度Δ˙γ系数增加，增大了弹体滚转运动的气动阻尼作用。

式（6）特征方程为：

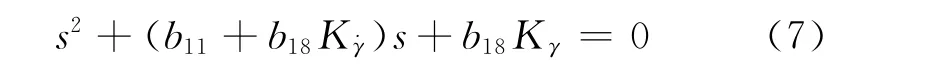
可得特征根为：

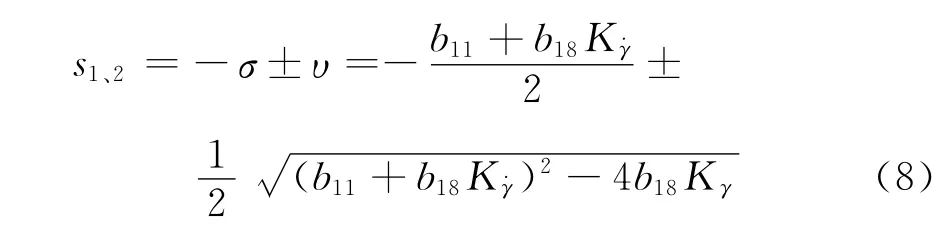
分析特征根式（8），存在两种可能的情况。当K˙γ取为0时，由于滚转阻尼动力系数b11为一小量，存在－4b18Kγ＜0，因此s1、2为一对共轭复根，滚转运动的自由运动为振荡运动，因为b11＞0，根的实部为负，所以滚转运动为衰减的振荡运动。

通过上述分析证明，采用式（5）的舵偏控制调节规律可以实现对滚转运动的自动稳定，满足増程制导炮弹滚转控制的要求。

3 滚转控制参数设计

基于上述分析建立某型制导炮弹的滚转运动自动驾驶仪仿真模型，设计该模型的滚转控制参数，通过调整控制参数Kγ、K˙γ可以实现自动驾驶仪对滚转运动的控制。控制参数设计采用基于MATLAB／Simlink的仿真软件平台，利用Simulink Response Optimization（SRO）模块进行控制参数优化设计。SRO是The MathWorks公司开发的一个基于Simulink的用于控制系统参数优化的设计工具［5］。

通过使用SRO模块，在给定的指标要求下，用Simulink对上述倾斜稳定回路进行建模，并对设计参数优化，获得性能优良的控制系统。

根据图1用Simulink建立滚转控制回路模型。控制回路时域品质指标为：上升时间tr＜0.15s，调节时间ts＜0.3s，超调量σ%＜5%，稳态误差ess＜0.05。

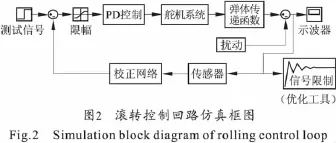
图2为基于Simulink建立的滚转控制回路模型，其中Signal Constraint即为SRO模块，在该模块中设置相应的参数，并进行优化计算，具体步骤如下：

1）按上述控制回路品质要求在SRO模块的Desired Response中设置品质指标参数。

2）在SRO模块的Optimization中定义需要优化的变量及其初值，设置参数初值Kγ＝1.5，K˙γ＝0.5，将其添加到Tuned Parameters下，并设置参数搜索范围的上下界为［0，100］，［0，100］。

3）设置优化算法，在Optimization Options中选择Gradient descent优化算法。

4）设置求解器，在Simulation Options中设置Fixes－step算法，求解器选为ode4，仿真步长0.001s，即采用固定步长的四阶龙格－库塔算法求解。

设置完成后开始进行优化，优化结果如图3所示。优化得出的参数值为 Kγ＝0.773 7，K˙γ＝0.042 2。

图3为SRO模块的Signal Constraint优化处理结果图，图中显示了Signal Constraint模块进行优化的中间结果以及最终结果，最优结果很好地满足了控制品质的指标要求。

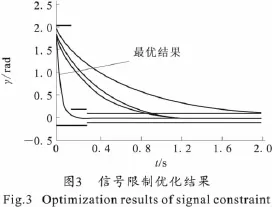
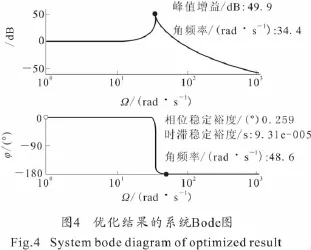
图4为滚转控制回路经Signal Constraint优化运算后，得出最优参数，控制系统选用此参数时的系统Bode图。

4 结 论

在建立増程制导炮弹侧向运动模型的基础上，通过简化分析得出制导炮弹滚转运动的数学模型。分析了滚转回路的动态特性，并根据分析结果设计了适当的倾斜自动驾驶仪。

采用PD控制方式实现对制导弹滚转通道的控制，控制参数的设计基于Simulink的SRO模块实现，采用该方法可以获得较好的设计结果，同时也极大地缩短了设计周期，具有较好的应用前景。

（References）

［1］吴甲生，雷娟棉.制导兵器气动布局与气动特性［M］.北京：国防工业出版社，2008.WU Jia－sheng，LEI Juan－mian，Aerodynamic configuration and characteristics of guided weapons［M］.Beijing：National Defense Industry Press，2008.（in Chinese）

［2］钱杏芳，林瑞雄，赵亚男.导弹飞行力学［M］.北京：北京理工大学出版社，2008.QIAN Xing－fang，LIN Rui－xiong，ZHAO Ya－nan.Flight dynamics of missiles［M］.Beijing：Beijing Institute of Technology Press，2008.（in Chinese）

［3］韩子鹏.弹箭外弹道学［M］.北京：北京理工大学出版社，2008.HAN Zi－peng，Exterior ballistics of missiles［M］.Beijing：Beijing Institute of Technology Press，2008.（in Chinese）

［4］李新国，方群.有翼导弹飞行动力学［M］.西安：西北工业大学出版社，2008.LI Xin－Guo，FANG Qun.Flight dynamics of winged missiles［M］.Xi’an：Northwestern Polytechnical University Press，2008.（in Chinese）

［5］朱汉卿，谷良贤.基于Simulink的导弹控制系统参数优化设计［J］.航天控制，2008，26（3）：79－82.ZHU Han－qing，GU Liang－xian.Parameter optimization design of missile control［J］.Aerospace Control，2008，26（3）：79－82.（in Chinese）