单边直线感应电动机直接推力控制方法研究

易一鹏，庄圣贤，周志超，程远银

(西南交通大学，四川成都610031)

0 引 言

直线电动机具有非粘着驱动牵引方式、调速性能稳定、加速快、噪声低、重量轻等优点。直线感应电动机作为其中重要的一个分支，近年来在工业和交通等领域的研究及应用中备受重视。如高速运载系统、滑动门、电梯、火箭发射装置等等［1］。

直线感应电动机(以下简称LIM)采用长直的两端开断结构，当初次级发生相对运动时，因纵向和横向边缘效应引起气隙磁场畸变，使得电机效率降低，因此其等效电路模型不像旋转感应电机那样简单［2］。磁场对电机控制性能的好坏起着决定性作用，因而分析其数学模型非常重要。经典的矢量控制和空间矢量调制方法已经被广泛应用于控制LIM［2］中，相对而言，响应速度快、控制方式简单的直接转矩控制方法在LIM控制上的研究近年来才兴起。文献［3］建立了静止参考坐标系下的LIM模型并应用了直接推力控制方法，但其模型是基于转子磁场定向而建立的。文献［4－5］从电机的不对称结构出发，应用直接转矩控制方法控制LIM，但在构建电机模型时，未把边缘效应的影响量化到等效模型中。本文建立了直线感应电动机静止坐标系下的数学模型，并基于Matlab/Simulink对该模型进行了直接推力控制仿真，仿真结果说明了边缘效应对LIM的运行性能影响很大，同时验证了电机模型和控制策略的正确性和有效性。

1 LIM模型分析

直线电动机可以看作为将普通的旋转电机沿轴线方向的平面剖开然后展开成直线形状而成［1］。对于短初级长次级单边LIM，其初级与旋转感应电机的定子绕组相对应，次级与转子绕组对应［2］。

由于这种特殊的结构，直线电动机在运行时会产生数种边缘效应［1］。其中横向边缘效应可以通过初、次级宽度的调整得到改善;静态纵向边缘效应可以通过各相绕组之间的换位或者增加极对数的方法得到改善［6］;但是动态纵向边缘效应的影响很大，在高速时尤为明显。

图1为短初级长次级的LIM模型。当电机初级以速度v运动时，某部分次级导体进入到初级下的气隙中，由于气隙磁链守恒，次级导体板闭合回路中除了产生与通常旋转电机中同样的感应电动势和电流外，还存在着由于闭合回路磁通发生变化而引起的感应涡流，这种感应电流会削弱气隙中的磁场;同样地，当次级导体板在离开初级时也会产生一种感应电流，这种感应电流加强气隙中的磁场。根据Duncan的理论，引入无单位量纲Q来修正旋转异步电动机模型，使边缘效应的影响量化入等效电路中［7］，无单位量纲Q定义:

图1 直线电机初级以速度v运动时在进入端和离开端产生涡流

式中:D表示电机的初级长度;R表示次级电阻;v表示电机直线速度;Llr表示次级漏感;Lm表示励磁电感。在电机参数一定时，其大小取决于速度。若速度为零时，则Q为无限长，边缘效应便可忽略。而随着速度的上升，该值就减小，LIM的励磁电流也减小，边缘效应的影响就会变大。

次级端部涡流损耗可以等效为在d轴励磁回路中串联一个的电阻。次级涡流的去磁作用可以等效为一个去磁电感，然后与原有励磁电感并联，得总励磁电感设边缘效应函数即总励磁电感:

在转子磁场定向矢量控制方法中，由于ψrd=|ψr|，ψrq=0，边缘效应对q轴磁链没有影响，可认为LIM的q轴电路与普通旋转感应电机q轴电路一样。在直接推力控制方法中，采用保持定子磁链恒定的方法，即:，边缘效应对d、q轴磁链均有影响。结合G.Kang的LIM模型［8］与异步电动机动态等效电路［9］，由上分析可得直线感应电动机在静止坐标系下的等效电路，如图2所示。

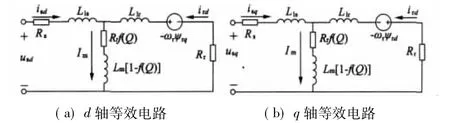
图2 直线感应电动机d－q等效电路

2 LIM方程的建立

根据等效电路写出电压方程(d轴变量用α表示，q轴变量用β表示):

式中:D表示电机的初级长度;Rs、Rr表示初级电阻、次级电阻;Lls、Llr、Lm表示初级漏感、次级漏感，励磁电感;isα、irα、isβ、irβ分别表示 α 轴初级电流、α轴次级电流，β轴初级电流、β轴次级电流。

由式(3)可得磁链计算式:

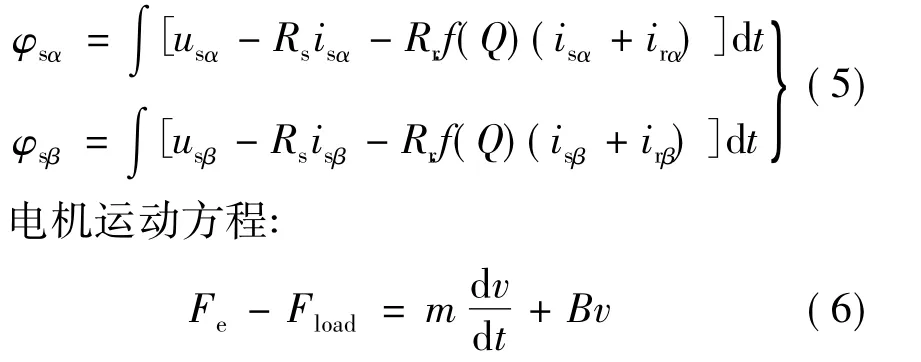
式中:m表示电机质量;B表示粘滞摩擦系数。

若ωr为直线电机等效角速度，它与v的关系，转矩Te与推力Fe的关系分别为:

式中:τ表示初级线组极距。

电磁推力方程式:

式中:p为电机极对数。根据式(4)、式(8)可得推力计算式:

由磁链方程可得电流计算式:

由式(3)推得磁链状态方程:

由运动方程得等效角速度状态方程:

把LIM的等效电路写成状态空间方程的形式，则:

LIM模型就是基于状态方程建立的。

3 直接推力控制模型

LIM的直接推力控制即是把直接转矩控制方法应用于LIM，其方法与旋转感应电机一样。如图3所示，控制模型主要由PWM逆变器、直线感应电动机、磁链与推力计算模块、磁链位置判断、磁链调节器、推力调节器、电压矢量选择器组成。系统给定值包括:设定电机速度定子磁链以及负载推力Fload。电机输出值包括:电机速度以及由速度计算所得的边缘效应函数f(Q)、定子电流。

图3 考虑边缘效应影响下的直接推力控制框图

三相PWM有8种不同的逻辑状态，可以输出8种不同的电压矢量，包括6个非零电压矢量和2个零电压矢量。电压矢量的选择由三个量共同决定:推力滞环输出eF、磁链滞环输出量eψ以及磁链扇区位置sector。

磁链调节器采用两电平滞环比较器，Hψ为磁链滞环宽度，表达式如下:

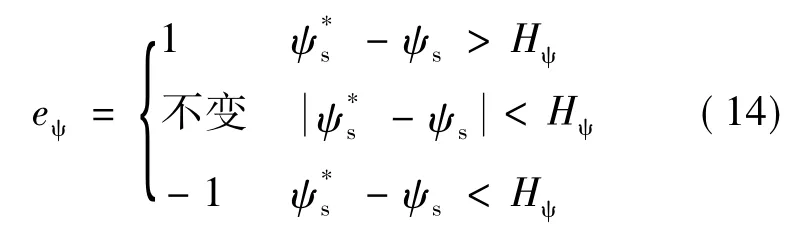
推力控制器采用三电平滞环比较器，HF为推力滞环宽度，表达式如下:

为了获得快速准确的推力响应，需要按照如表1所示的规则选择电压矢量施加给LIM，便可将磁链和推力的波动范围严格限制在其滞环宽度范围内。

表1 电压矢量控制选择表

4 结果及分析

仿真用直线电动机参数如表2所示，给定定子磁链│ψs│=0.45 Wb，磁链滞环宽度设定为Hψ=0.005 Wb，推力滞环宽度设定为HF=0.01 N，电机推力限制值Fmax=2 385 N。

表2 直线电机参数表

(1)f(Q)与速度、互感与速度的关系

图4a为f(Q)与电机速度v的关系，图4b为电机励磁电感L'm与速度v的关系。由图4可知随着速度的上升，边缘效应的效果会增强，总励磁电感值随着电机速度的上升而下降。

图4 f(Q)、励磁电感与速度的关系

(2)空载时速度突变

以下为不考虑和考虑边缘效应影响下的仿真结果对比。电机负载为空载;运行速度设置为:0～0.5s:2 m/s，0.5 ～1 s:8 m/s。

图5为三相定子电流波形图，图6为圆形定子磁链轨迹，图7为电机速度响应对比，图8表示给定速度为8 m/s时的放大对比，图9为电机推力响应对比。

如图8、图9所示，经过放大对比，当建立的电机控制模型不考虑边缘效应影响时，速度和推力振荡幅度明显大于考虑边缘效应影响时的，而且这种现象还会随着电机速度v的上升而加剧，这是由于磁链和推力计算模型中没有准确反映边缘效应影响所造成的。而考虑了边缘效应后，磁链和推力方程分别如式(4)和式(8)所示，LIM最终产生的速度和推力响应的振荡幅度大为减小。

仿真结果表明，直接推力控制方法在LIM控制上取得了较为理想的效果，当速度指令值突变时，电机的动态响应速度快，稳态性能好。考虑动态纵向边缘效应影响之后，LIM的运行性能得到有效改善。

5 结 语

本文将直接转矩控制方法引入到LIM控制中，并将其特有的边缘效应影响量化入等效电路中，实现了LIM的直接推力控制。仿真结果凸显出直接推力控制方法在LIM控制上的简单、快速有效性，同时说明了动态纵向边缘效应对LIM运行时的速度和推力的振荡幅度影响很大，不可忽视。在工程实际中，随着运行环境的改变，LIM的各项参数通常是非线性、强耦合且时变的，必须建立更为正确有效的控制模型加以克服。

［1]Gieras J F.Linear Induction Drives［M］.Oxford Science Publications，1994.

［2]Sung J H，Nam K H.A new approach to vector control for a linear induction motor considering end effects［J］.Thirty－Fourth IAS Annual Meeting on Industry Application，1999(4):2284－2289.

［3]Susluoglu B，Karsli V M.Direct thrust controlled linear induction motor including end effect［C］//Power Electronics and Motion Control Conference.2008:850－854.

［4]Ozkop E，Akpinar A S，Okumus H I.Direct torque control for linear induction motor［C］//Power System Conference.2008:373－376.

［5]Itoh K，Kubota H.Thrust ripple reduction of linear induction motor with direct torque control［J］.Proc.of the ICEMS，2005(1):655－658.

［6]叶云岳.直线电机原理与应用［M］.北京:机械工业出版社，2000:40－48.

［7]Duncan J，Eng C.Linear induction motor－equivalent circuit model［J］.IEE Proc.on Electric.Power Applications，1983，130(1):51－57.

［8]Kang G，Nam K.Field－oriented control scheme for linear induction motor with the end effect［J］.IEE Proc.Electric Power Appl.，2005，152(6):1565－1572 .

［9]陈伯时，陈敏逊.交流调速系统［M］.北京:机械工业出版社，2006:184～188.