屈曲约束支撑钢框架的地震反应分析

王德伟 常彦铮

0 引言

钢结构轻质高强，抗震性能好。纯钢框架侧向刚度较差，往往需要较大的梁、柱截面才能满足要求，中心支撑钢框架的支撑在强震作用下易发生屈曲失稳，造成其抗震能力急剧下降，偏心支撑钢框架的支撑在一定程度上解决了上述结构体系中存在的问题，但在强震下仍有支撑屈曲、拉压滞回性能不对称等问题。为了改善支撑的受力性能，使其在地震作用时不发生屈曲，屈曲约束支撑钢框架(BRBFs)体系应运而生。这种体系在发达国家已被大量采用，国内的应用研究正在不断发展中。本文主要将BRBFs结构体系与普通中心支撑钢框架进行对比探讨分析。

1 结构计算模型

1.1 屈曲约束支撑钢框架设计方法及原则

本文屈曲支撑钢框架模型基于抗侧刚度比的方法进行设计。

在屈曲约束支撑钢框架的设计中，要保证支撑能够充分发挥其性能:1)要求支撑要先于框架部分屈服，进行耗能，减少传递到框架部分的能量，对框架起到保护作用;2)合理把握支撑的截面面积，如果增大支撑的截面面积，则结构的抗侧刚度也随之增大，水平荷载不变的情况下，框架的侧移将随之减小，但是刚度增大同时会导致整个结构受到的地震作用增强。因此支撑与框架的刚度之间的匹配程度对整个结构的地震响应有着重要影响。

支撑钢框架结构的抗侧刚度比表达式如下:

其中，k为整个支撑框架结构的抗侧刚度比;Kd为应用D值法确定的框架部分的抗侧刚度;Kb为支撑提供的弹性水平抗侧刚度。

其中，θ为屈曲支撑的倾角;h为柱高。

抗侧刚度比k对结构性能的影响，已有一定的研究成果，文献[1]提出:“对于弹塑性时程分析，按照大震不倒的要求，确定k的合理取值范围介于0.5与2之间。”

1.2 计算模型设计

根据屈曲支撑钢框架的设计原则及步骤，设计8层3跨平面人字形屈曲支撑钢框架，根据我国《建筑抗震设计规范》[1]设计普通中心支撑钢框架。假定建筑场地信息，如表1所示。

表1 建筑场地信息

框架梁柱刚接，支撑与梁柱节点采用铰接;梁、柱及普通支撑截面均选用H型钢，钢材屈服强度为235 N/mm2;楼面恒荷载取4.5 kN/m2，活载为2.5 kN/m2;弹性最大层间位移角限值1/300，塑性最大层间位移角为1/50，结构立面如图1所示。

表2 构件截面尺寸

表3 各层屈曲约束支撑面积

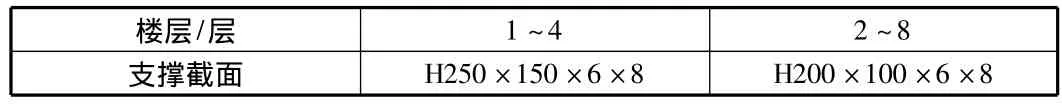
表4 各层普通支撑截面

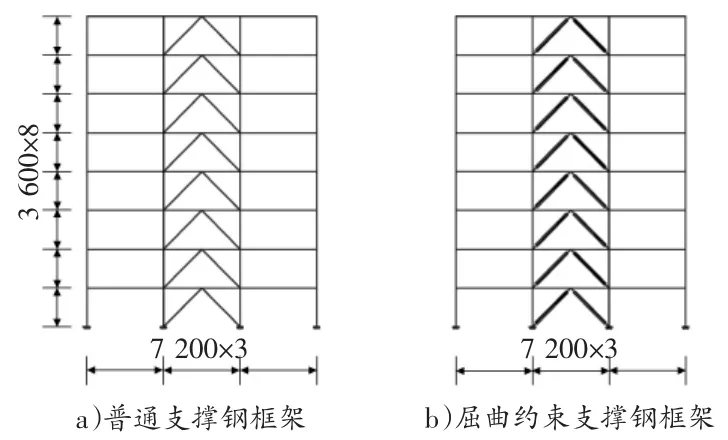
图1 结构立面简图

根据框架承担竖向荷载及部分水平荷载，框架梁柱截面尺寸见表2。

取抗侧刚度比k=2，根据式(3)可计算支撑内核面积A。

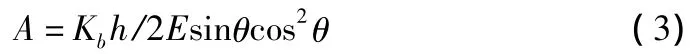
计算屈曲约束支撑面积如表3所示。

普通支撑钢框架的支撑截面根据屈曲约束支撑等效轴力得到，其各层截面如表4所示。

1.3 有限元模型

普通支撑钢框架梁、柱、支撑及屈曲约束支撑钢框架的梁、柱均选用Beam189单元模拟，Beam189是二次3-D梁单元，每个节点有6个～7个自由度[2]。对支撑杆件施加初始弯曲来模拟普通支撑在地震作用下先发生屈曲而退出工作。屈曲约束支撑采用Link8单元模拟，这个三维的杆元素每个节点上有3个自由度:x，y和z方向的位移，只考虑单轴的拉压，不考虑弯曲屈曲，是一种能用于模拟于桁架，杆件，弹簧等的单元。支撑的材料非线性为双线性随动强化模型，屈服点为235 N/mm2，屈服后强化阶段弹性模量为屈服前弹性模量的3%。

采用Mass21单元模拟重力荷载代表值，按荷载规范由恒载和活载组合而成，扣除结构自重(beam189单元输入密度自动计算)，其余由Mass单元质量块均布在每层的所有梁柱节点上。

2 时程分析

2.1 阻尼的选用

采用瑞利阻尼，其表达式为:

其中，c为瑞利阻尼矩阵;m为质量矩阵;k为刚度矩阵;a0为质量比例阻尼;a1为刚度比例阻尼。若已知两个特定频率(振型)ωm，ωn及相关阻尼比ξ，则a0，a1的求解可按下式计算:

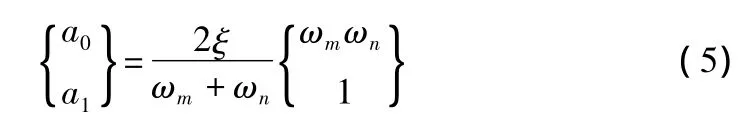
结构阻尼比ξ在基本烈度作用下取值为0.035。ωm，ωn取结构模态分析所得前两阶圆频率 ω1，ω2[3]。

2.2 地震波的选取

地震波选择的正确与否是进行结构时程分析的一个重要问题。本文按照文献[4]中的选波原则选取了四条地震波(如表5所示)。

表5 所选地震波列表

根据所选地震波的加速度记录，做出其对应的标准加速度反应谱(β谱)和平均反应谱与根据《01规范》转换成的场地设计反应谱(β谱)进行对比，如图2所示。

图2 反应谱对比

(0.1 s，0.4 s)平台段，所选地震波所对应的加速度反应谱平均值为2.508，规范反应谱的值为2.577，误差为2.8%;在基本周期附近所选地震波所对应的加速度反应谱平均值为1.597，规范反应谱的值为1.504，误差为6.2%。

3 结果分析

为分析结构在小震及大震中的响应，将上述四条地震波峰值加速度分别调整为70 cm/s2(小震)和400 cm/s2(大震)两种工况对结构进行时程分析。

3.1 小震作用下的结构响应

由图3，图4可知，在小震作用下，两种支撑结构均是:第1层和第8层间位移相对较小，2层～7层的层间相对位移平均值相差不大，但不同地震波间的相对层间位移相差较为明显。两种支撑结构的层间相对位移最大值均出现在3号波作用下的第3层，屈曲约束支撑钢框架的最大层间相对位移为0.0042 m，普通支撑钢框架的最大层间相对位移为0.0048 m，均小于层高的1/300(0.012 m)，满足《01规范》中关于多遇地震作用下弹性层间位移角限值要求。

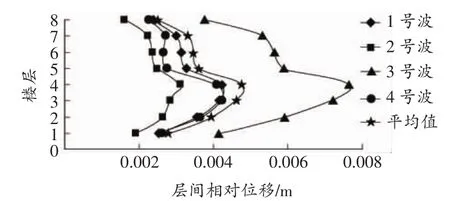
图3 屈曲约束支撑钢框架相对层间位移（一）

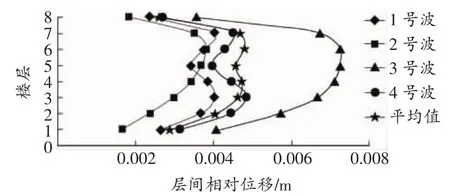
图4 普通支撑钢框架相对层间位移（一）

3.2 大震作用下的结构响应

由图5，图6可知，在大震作用下，普通支撑的各层层间相对位移差别较大。主要是由于结构中的普通支撑发生平面外失稳，导致整个结构的抗侧刚度分布不再均匀，而屈曲约束支撑的各层平均相对位移相比仍无较大的差别。屈曲约束支撑钢框架的最大层间相对位移发生在3号波作用下的第4层，值为0.0432，普通支撑钢框架层间相对位移发生在3号波作用下的第3层，值为0.0437，均小于层高的1/50(0.072 m)，满足《01规范》中关于罕遇地震作用下层间位移角限值要求。

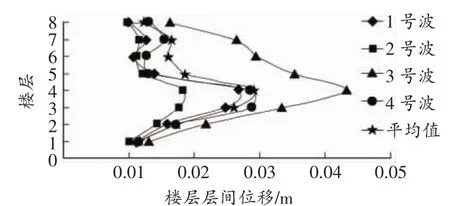
图5 屈曲约束支撑钢框架相对层间位移（二）

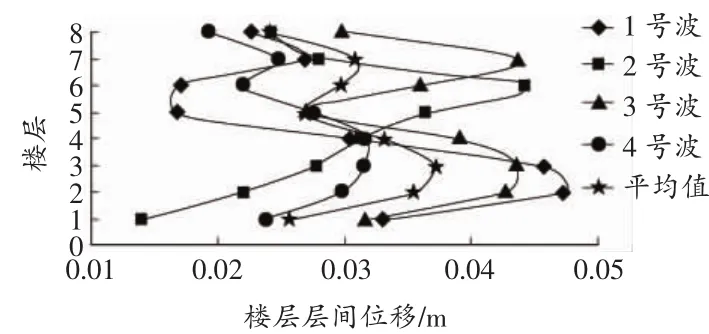
图6 普通支撑钢框架相对层间位移（二）

在侧向力作用下，柱、支撑所分担的剪力对其抗侧刚度影响较大，普通支撑由于受压发生失稳，导致整个结构的抗侧刚度退化较为严重。2号波地震作用下的底层柱、支撑分担的剪力见表6。

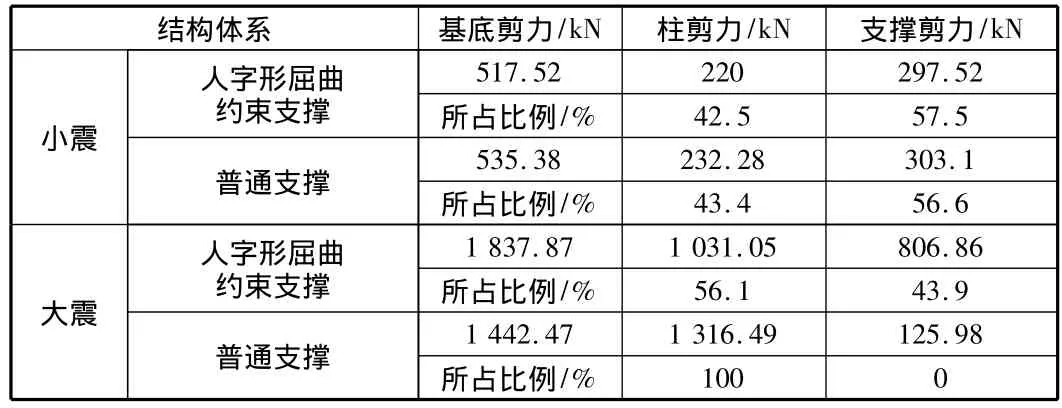
表6 2号波底层柱及支撑水平剪力时程最大值

小震作用下，普通支撑与屈曲约束支撑承担的结构剪力相差不大，但在大震作用下，普通支撑发生侧向屈曲，其承担的剪力可忽略不计，对于屈曲约束支撑，由于其芯材的屈曲行为受到约束单元的约束，而使得其能够继续为结构提供侧向刚度。

4 结语

1)在小震作用下，两种框架均满足规范要求，说明两种结构抗震性能良好;

2)在罕遇地震作用下弹塑性时程分析结果显示，普通支撑钢框架由于支撑的平面外失稳，导致整个结构刚度退化较为严重，从而加剧了结构的地震响应;

3)通过对大震作用下的屈曲约束支撑结构和普通支撑结构的底层支撑的剪力分担率分析可知，屈曲约束支撑对于提高钢框架的抗侧刚度表现更稳定;

4)屈曲约束支撑钢框架结构体系相对于普通支撑能够更好的发挥钢材的屈服耗能的性能，大震作用下能更加有效地保持结构的抗侧移刚度，控制结构的侧移，减小结构的地震响应。因此屈曲约束支撑更适合作为具有更高抗侧力和抗震要求的支撑框架结构体系的水平抗力构件。

[1]GB 50011-2001，建筑抗震设计规范[S].

[2]龚曙光，谢桂兰.ANSYS操作命令与参数化编程[M].北京:机械工业出版社，2004.

[3][美]R·克拉夫，J·彭津.结构动力学[M].北京:高等教育出版社，2006.

[4]杨 博，李英民，赖 明.结构时程分析法输入地震波的选择控制指标[J].土木工程学报，2000，33(6):35.