重力坝坝基失稳模糊-随机风险率计算方法研究

2011-06-13彭慧慧马震岳

大坝与安全 2011年4期

彭慧慧，王刚，马震岳

（大连理工大学建设工程学部，辽宁大连 116024）

0 前言

目前在重力坝抗滑稳定性分析中，一般通过刚体平衡法计算安全系数来评价，此方法原理简单，实用性强，能够直接提供坝体稳定性的定量结果，所以能被广泛应用。但在实际工程中，用安全系数来评价坝基的稳定性往往具有局限性，因为规范中的安全系数主要是根据工程经验确定的，并没有考虑到影响安全系数的各个参数变量的不确定性。大量的试验和工程实践证明，影响大坝稳定状态的因素中，有许多具有明显的随机性和模糊性，如坝基岩石与坝体材料的强度参数、外界荷载、边界条件、地下水、岩土体内的各种不连续面等，用确定性方法进行计算评价往往会带来很大的误差，甚至结果失真[1]，因此，有必要将基于随机性与模糊性的风险分析应用于大坝稳定性评价中，概率风险分析也已经成为大坝安全领域一个必不可少的评价方法。本文综合考虑影响大坝稳定各因素的随机性、模糊性以及稳定失效准则的模糊性，建立大坝失稳的模糊风险分析模型，定量分析大坝的稳定性，并根据允许风险值来评估大坝失稳的概率。

1 重力坝坝基稳定允许风险标准

大坝安全风险分析的目的之一就是通过计算大坝的风险概率来评价坝的安全性，以便决定是否需要采取提高安全性的措施，进而为风险决策和风险管理奠定基础。风险分析需要一个统一的风险标准来衡量计算结果，然而，风险标准取值问题是政治、经济、环境与大坝安全之间的权衡问题，因此，本文仅就一般情况提出坝体失稳风险标准，对于一旦发生坝体失稳可能导致严重后果的，须视具体情况，提高风险限值。

就风险标准的确定方法而言，目前国外较为盛行的是“容许风险分析方法”[2]。参考国外不同坝型的失事统计概率，借鉴其它国家的风险标准，再结合我国的实际情况，我国大坝风险分析参考的风险标准为[3]：大、中型水库大坝，小于1.1×10-4/年，超过1.0×10-3/年是不可容忍的；对于小型水库，小于2.8×10-4/年的风险是可以接受的，超过2.8×10-3/年的风险是不可容忍的。而本文重点研究坝基失稳的风险。据有关统计资料，因坝体失稳造成大坝失事的数量约占大坝失事总数的不到0.1个数量级，因此，对于大坝失稳的风险标准可取为：大、中型水库大坝，小于1.1×10-5/年，超过1.0×10-4/年是不可容忍的；对于小型水库，小于2.8×10-5/年的风险是可以接受的，超过2.8×10-4/年的风险是不可容忍的。

2 模糊-随机风险率计算方法

2.1 随机参数的敏感性与相关性分析

计算风险率的方法有很多，其中JC法应用较为广泛。此方法对统计独立的变量和具有线性极限状态方程的情况是很精确的，我国现行规范也规定采用此方法计算结构可靠度，因此也采用此方法计算大坝失稳风险率。影响大坝失稳的因素很多，对其模糊不确定性的研究也是一项极其复杂的工作，某些模糊不确定性的研究还极其困难。为能简化研究又不失去其价值，可先利用JC法对大坝抗滑稳定分析中的各影响因素进行敏感性分析，得出主要敏感因子和非敏感因子，忽略非敏感因子，再对主要的敏感因子进行模糊处理，从而有效简化模糊风险率的研究和分析。

JC法的原理是通过式（1）、（2）迭代求得可靠度指标：

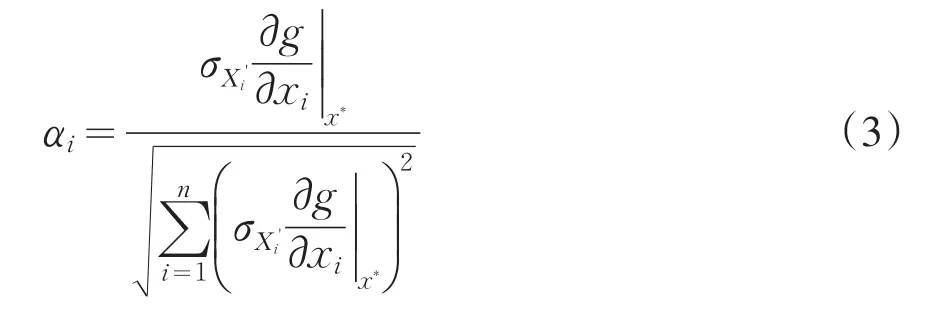
根据有关文献及对实测资料的统计分析结果表明[5-7]，变量f'和c'通常存在负相关性，而且线性相关系数多在-0.6～-0.9之间。可利用正交变换法先将相关正态随机变量变为独立正态随机变量，再用JC法计算失效概率。

设基本随机变量{X}=(x1,x2,…,xn)T为相关的正态分布随机变量，先通过{X}的协方差矩阵[Cx]得到能将{X}正交化的矩阵{A}，从而将相关的变量{X}变成一组不相关的变量{Y}，然后将不相关的正态变量{Y}标准化或正则化，得到另外一组正则化的不相关变量{Z}=(z1,z2,…,zn)T，最后在Z空间中求出可靠指标和失效概率[8]。

2.2 参数与失效准则模糊性的考虑

大坝的稳定状态受众多因素或变量的影响，如水位、岩土体的物理力学性质指标、大坝的结构尺寸、地震的动力效应等，其中水位和岩土体的力学参数对失稳影响最大。在计算失稳模糊风险率时，对于水位仅考虑其随机性，而对岩土体物理力学指标，因摩擦系数和凝聚力的变异性影响程度最大，也最为重要，所以将其随机性和模糊性均考虑到模糊风险的计算中。

对于失效准则，传统的风险理论以Z＝0作为度量大坝是否失效的界限，在零点两侧，结构的失效和安全状态是以突变形式转化的，但大坝从安全到破坏很难用明确的界限来划分，在可靠与失效之间存在着一个中间过渡状态，是一个模糊范围。可将大坝失稳视为一模糊事件，用隶属函数来表示发生失稳的程度，然后根据模糊概率的定义，建立大坝失稳的概率计算数学模型，得出失效准则模糊时的大坝失稳模糊风险率。

2.3 模糊风险模型的建立与求解

关于模糊风险模型的建立，文献[9]中已做了较详细的分析，本文在此基础上着重分析模型的求解。

2.3.1 参数的模糊处理

由于事先无法确定设计参数的模糊隶属函数，假设基本随机变量均值的取值范围是（a，b），一般可以用图1中的曲线来刻画变量的模糊状态。

引入α水平截集，α∈[0,1]，可得到设计参数均值的模糊区间ω为：

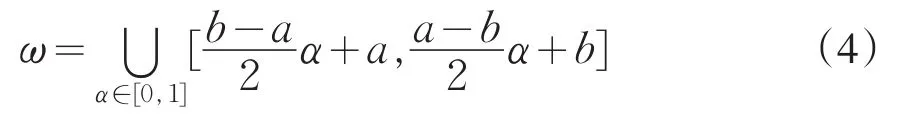
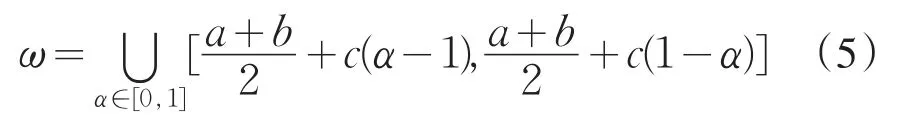
式中，c的取值反映随机变量均值的模糊边界范围，根据工程实际一般取c=10%×，由此又可将模糊区间简化为：

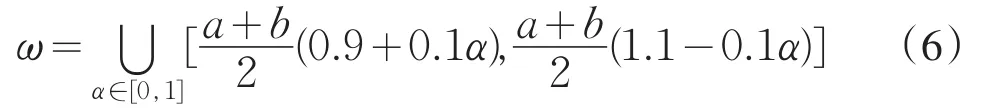
式中，α为模糊状态的约束变量，反映设计参数取值的模糊程度：α越小，模糊性越大；α越大，模糊性越小；当α=1时，模糊区间则为一点，即未考虑设计参数的模糊性。

图1 设计参数模糊化处理Fig.1 Fuzzy processing of the design parameters

2.3.2 失效准则的模糊处理

失效准则的模糊性可通过模糊随机极限状态方程表示为

式中的∈为一模糊数，表示大坝稳定由安全状态到失效状态的渐变过程。

与设计参数的模糊化处理相似，可以用图2的三角模糊数来刻画失效准则的模糊状态，引入α水平截集，α∈[0，1]，可得到失效准则的模糊区间为

式中，δ为极限状态的最大容许值，这需根据实际工程情况和管理情况而定，是一个主观值，在实际计算时应由多位专家研究确定。而且若以式（7）作为极限状态方程时，∈为一具体的安全储备值，不同工程的取值会相差很大，难以在计算研究中对安全储备值获得较普遍的规律，因此，建立基于安全系数的极限状态方程如下：

由概率知识可知：

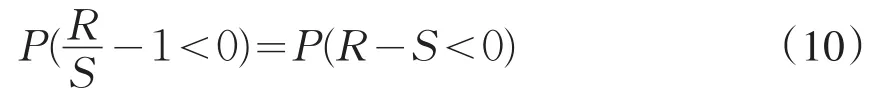
所以式（9）可以代替基于安全储备值的极限状态方程进行模糊风险率的研究，基于安全系数法的模糊随机极限状态方程为

此时的∈为安全系数的一个模糊范围，也可用α水平截集得到类似式（8）的模糊区间，而本文将根据安全系数的取值特征对∈的隶属函数和模糊范围进行研究探讨。

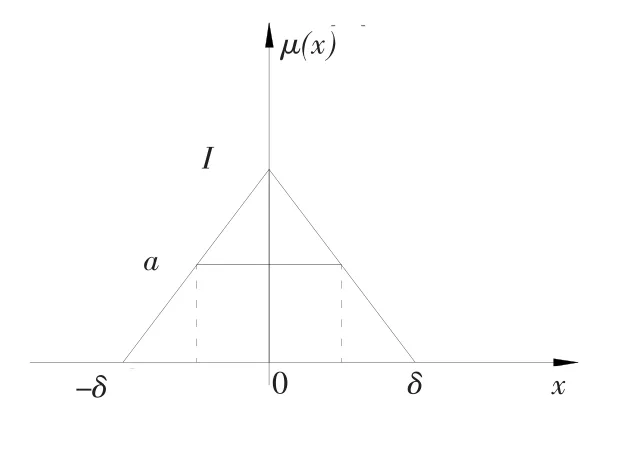
图2 三角模糊数Fig.2 Triangular fuzzy number

设失效准则的隶属函数为μ∈（z），模糊区间为（a，b），通过分析可知：当z≤a时，结构失效，对失效概率的隶属度为1，即μ∈（z）=1；z＞b时，结构可靠，对失效概率的隶属度为0，即μ∈（z）=0；当a＜z≤b时，结构安全状态模糊，z值由a增大到b的过程也是结构由失效到可靠的过程，对失效概率的隶属度由1逐渐减小到0。

由此特点可将失效准则的隶属函数取为偏下型模糊分布[10]，如降半梯形或降半岭形分布，其中的待定系数根据实际工程经验与统计确定。选取降半梯形隶属函数对失效准则进行模糊分析研究，形式如下：

2.3.3 模糊风险率的计算

对设计参数采用α水平截集法进行模糊，而对失效准则利用降半梯形隶属函数进行模糊，有

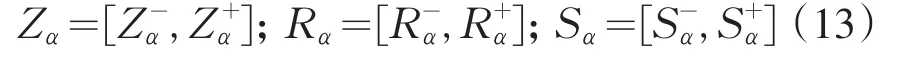
则模糊随机极限状态方程变为

模糊风险率的上下限值分别为

由此可得模糊风险为

3 工程应用

为了说明坝基失稳模糊风险分析方法的应用，根据前述理论和步骤，以某长服役期重力坝典型坝段为例进行分析（剖面图见图3）。坝基抗滑稳定计算中考虑抗剪断摩擦系数f'、凝聚力c'、混凝土重度γ、上游水位hu、下游水位hd、上游淤沙高度hs和扬压力折减系数α等7个随机变量，水重度按常量γw=9.8 kN/m3处理。取正常蓄水位工况下整个坝段进行分析，坝宽为18 m，其统计特征见表1。

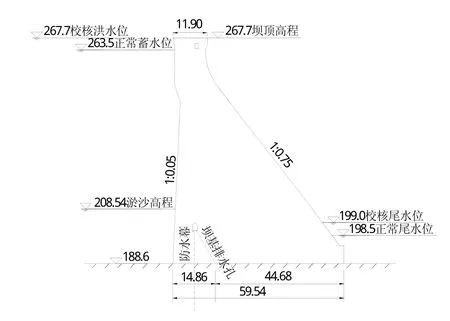
图3 典型重力坝剖面（单位：m）Fig.3 Typical cross section of the gravity dam

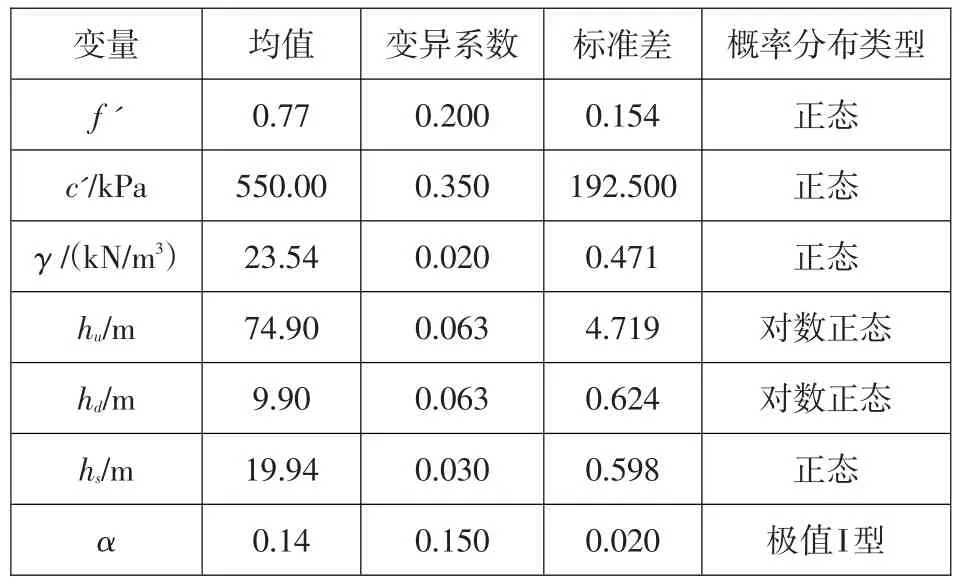
表1 随机变量统计特征Table 1:Statistical characteristics of the random variables

坝基抗滑稳定功能函数采用基于安全储备值的功能函数，取为：

式中：U为坝底扬压力，ΣW为坝体自重，ΣP包括上下游静水压力、淤沙压力，A为坝底面积。

3.1 敏感性分析

假设各变量相互独立，计算求得坝基抗滑稳定可靠度指标、随机风险率及各随机变量验算点、敏感系数见表2，可得到各变量敏感度图，见图4。

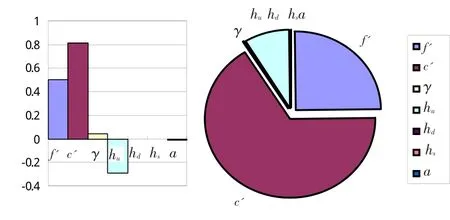
图4 各变量敏感度图Fig.4 Sensitivities of the variables

表2 可靠指标、验算点及敏感系数Table 2:Reliability indexes,checking points and sensitivity coefficients

由表2及图4可看出，粘聚力c'为第一敏感因素，敏感系数为0.813 7，其次分别是抗剪断摩擦系数f'及上游水位hu，对坝基失稳风险率也有着较大的影响，这三个参数可作为主要敏感因素，下文进行详细分析讨论；而其他随机变量γ、hd、hs和α的敏感系数非常小，最大的还不到0.05%，可列为非敏感因素，计算时作为常量考虑即可。

3.2 参数相关性分析

f'和c'一般呈负相关性，为了研究其相关性对坝基失稳风险率的影响，考虑f'和c'的负相关性，取值由-1.0到0，不考虑其他变量的相关性，计算结果见表3。

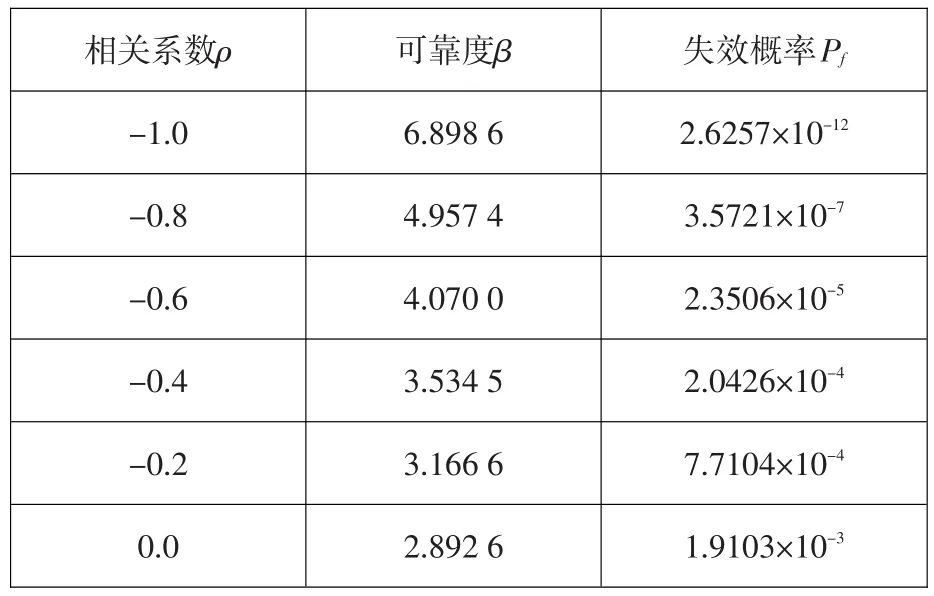
表3 相关系数ρ对可靠度指标和失效概率的影响Table 3:Influence of correlation coefficient on reliability index and failure probability

计算结果表明：相关系数ρ对失效概率Pf值的确有影响，当ρ从-0.6增加到0时,可靠指标β值从4.070 0减小到2.892 6，减小量为1.177 4，失效概率Pf从2.3506×10-5增加到1.9103×10-3，增加了近两个数量级，由此可知，当f'和c'呈现负相关关系时,失效概率Pf值随相关系数ρ的绝对值的增大而减小，不考虑负相关时的计算结果偏于安全。

3.3 忽略非敏感因子后的影响分析

忽略非敏感因素的随机性，将γ、hd、hs和α分别按定值代入，使功能函数简化为只关于主要敏感因子f'、c'和hu的函数：

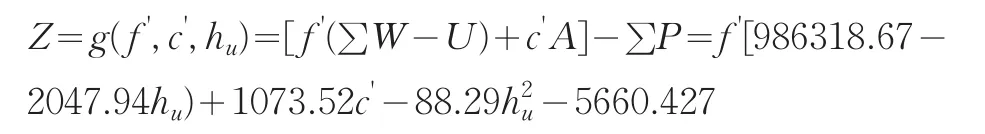
简化后计算所得结果与简化前的结果进行比较，见表4。

从表4中可看出，简化后计算所得的安全指标均变化很小，不考虑f'和c'相关时得到的失效概率变化不到0.2%，而考虑相关时也相差不到6%，因此，忽略其他非敏感因素的随机性对失稳风险率的影响不大，可以采用此功能函数进行模糊风险分析。

3.4 设计参数与失效准则分别具有模糊性时模糊风险率的计算

采用式（9）的极限状态方程，则简化后的功能函数为:

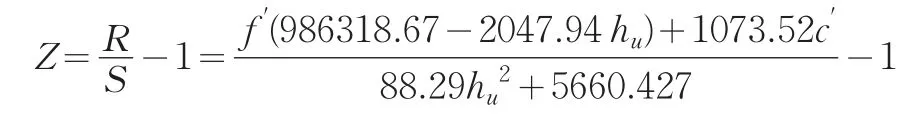
忽略非敏感因子后按式（6）对随机变量f'和c'进行模糊化，取α=0.5时的截集计算失效概率，结果见表5。

表4 忽略随机性对可靠指标的影响程度Table 4:Influence of randomness on reliability index neglected

表5 α=0.5时的模糊失效概率Table 5:The fuzzy failure probability while α=0.5

考虑失效准则的模糊时将坝基失稳准则∈作为模糊随机事件，其隶属函数μ∈（z）取作式（12）的降半梯形分布。为便于研究，暂取a=-0.5，b=0.5，计算模糊失效准则下的模糊随机风险率，结果为Pf=8.6960×10-3。

3.5 失效准则和设计参数均具有模糊性时模糊风险率的计算

采用α水平截集法对设计参数进行模糊（α=0.5），失效准则的模糊分别采用两种方法进行模糊：①本文方法，以上述隶属函数进行模糊；②采用水平截集法，截集与模糊区间（a，b）相同。取不同模糊区间，计算结果见表6。

表6 模糊随机风险率计算结果Table 6:Calculation results of the fuzzy random risk rate

由表6中数据可以看出，除了（-0.1,0.1），采用其他模糊区间时，本文方法所得到的风险率区间宽度都比方法②的小。模糊区间取（-0.3，0.3）时，两种方法得到的均值基本一致，变量的模糊与失效准则的模糊对风险率的影响程度也差不多；而小于此区间时，方法①得到的均值都大于方法②，变量的模糊对风险率的影响更大；大于此区间时，方法①的均值都小于方法②，失效准则的模糊对风险率的影响更大。为了较好地体现变量和失效准则的模糊性对风险率的影响，取模糊区间为（-0.3，0.3）时本文方法得到的模糊风险率，即[2.9337×10-3，5.9645×10-3]，均值为4.4491×10-3。

上述分析是在假定各变量相互独立的前提下进行的，考虑变量f'和c'的相关性进行计算比较，结果见表7。

从表7中可以看出，无论是方法①还是方法②，考虑f'和c'负相关时的模糊风险率都比不相关时有所减小，减小的程度与相关系数绝对值大小成正比。而且变量的模糊对风险率的影响程度会因变量相关而发生改变：相关系数的绝对值越大，变量的模糊对风险率的影响程度也越大。由于f'和c'一般为负相关，取ρ=-0.6时的模糊风险率进行评价，为[1.5777×10-3，3.4798×10-3]，均值为2.5288×10-3。

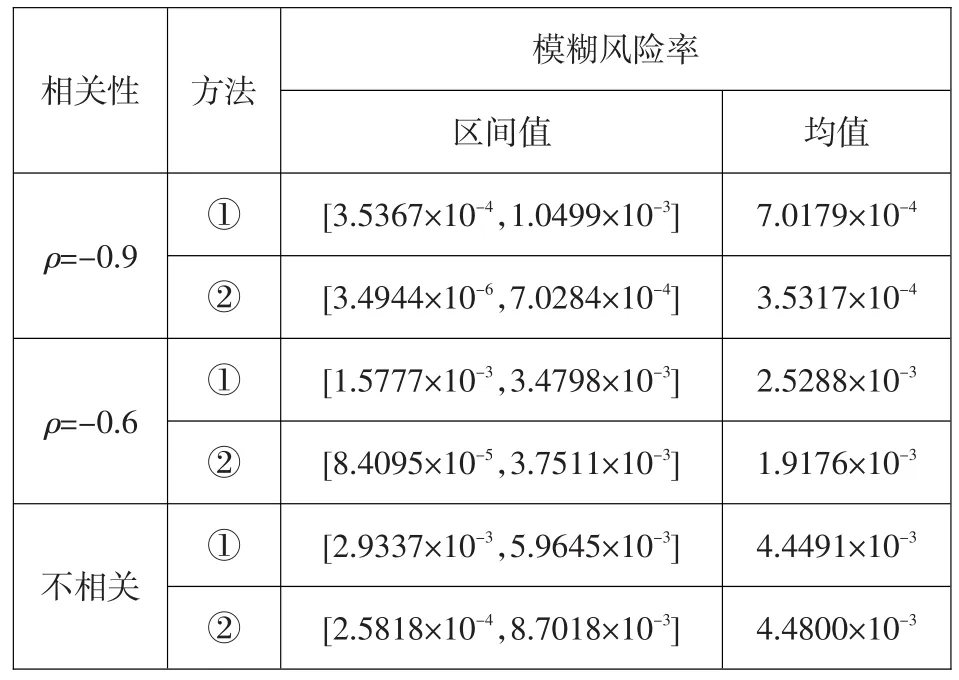
表7 模糊区间取（-0.3,0.3），考虑相关时所得模糊风险率比较Table 7:The fuzzy risk rates under correlation condition and on the fuzzy interval(-0.3,0.3)

该大坝具有重要的社会及区域经济作用，一旦失事将给下游带来巨大损失，根据本文提出的该大坝相应等级失稳风险评价标准，风险率超过1.0×10-4是不可容忍的。由计算结果可以看出，不管是否考虑参数相关性，该坝段计算所得的模糊风险率均超过此标准，表明该大坝存在较大的安全隐患，这与文献[11]中的结论一致。而且，根据现行规范的刚体平衡法计算得到的安全系数为2.459，小于3.0的允许值，不满足规范的要求。