基于MATLAB的探地雷达堤坝隐患探测仿真研究

刘世奇,李 钰

（1.湖南省水利厅，湖南 长沙 410001；2.华东理工大学信息学院，上海 200237）

0 前 言

堤坝隐患一直是水利建设中的大事，探地雷达是堤坝隐患检测中一种十分重要的方法。对探地雷达电磁波的传播过程进行计算机仿真有利于水利工程师更好地使用探地雷达进行堤坝的隐患排查。目前电磁波探测的技术原理有很多种，如Goodman和Mcchan等人于1995年提出的基于射线的方法,Zeng等人[1]提出的基于频域的方法以及Casper等人提出的伪谱方法。但是，这些方法都有一定的局限性，只有在各自特定的条件下才能取得比较好的性能。目前为止，有限差分法（FDTD）在电磁波媒质传播的模拟中应用得最为广泛[2]，效果也比较好，并且适合任意复杂媒质中波的传播。本文在Matlab软件中通过建立隐患的理论模型，利用FDTD方法来进行仿真，得出了电磁波在到达隐患表面时的一些传输特征，对实际堤坝检测中及时发现隐患具有重要的理论指导意义。

1 探地雷达计算机仿真的理论基础

探地雷达的数值模拟可以从两个麦克斯韦旋度方程开始[3，4]：

由于仿真空间不可能是无限的，所以在本程序中采用了卷积PML吸收边界条件来抑制边界区域波的反射。在这一边界条件下，计算过程中就可以将有效边界区域和吸收边界区域分离开来考虑，对程序的编制比较方便。同时，诸多研究也表明基于卷积PML的吸收边界方法具有很好的性能，吸收边界层的网格可以比较少，对计算复杂性也带来很多好处。为应用PML吸收边界条件[5]，采用了带伸缩因子的复坐标空间。因此，可以将微分操作符∇表示成：

其中：

上式中l=x,y,z。

在探地雷达数值模拟过程中，考虑波的传播方向为+y方向，与x-z平面垂直，这时，探地雷达工作在TM模式下，涉及的场量为、、三个量。所以麦克斯韦方程可以进一步简化为：

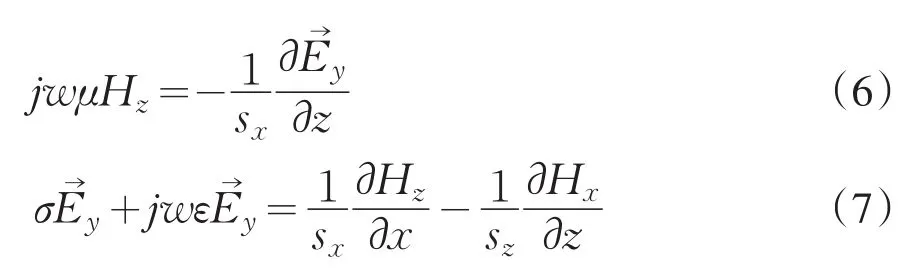
在有效计算区域内部，假设sx和sz都为1，在吸收边界网格内这两个参数可以通过式（4）进行计算。为用时域有限差分法来逼近式（5）～（7），采用了经典的Yee网格。计算过程中，所有空间导数利用四阶差分进行逼近，以达到尽可能高的精确度。时间导数采用二阶差分进行逼近。

时域有限差分法应用的一个重要步骤是进行时间离散参数Δt和空间离散参数的选择。假如空间离散参数Δx、Δz和Δt比较大的话，那么网格数目就会比较少，计算速度就会比较快。但是，参数Δt过大将导致数值不稳定，参数Δx和Δz过大将导致空间采样率不够，发生数值色散。为了使整个正演模拟计算过程数值稳定，采用以下原则进行时间离散参数的选择[2]：

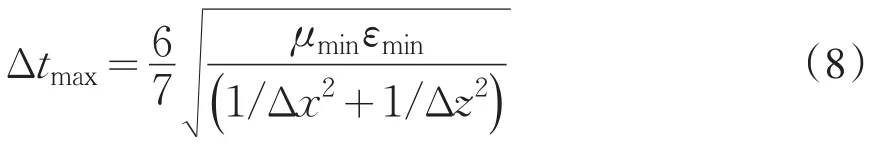
其中，μmin和εmin分别为计算模型中媒质的最小磁导率和最小介电常数。

对空间离散参数Δx和Δz的选择，在程序中按照保证电磁波在媒质中传播一个波长上至少被空间采样五次这样的原则来确定。

卷积PML吸收边界条件[6,7]能使电磁波在经过少量吸收边界网格后就得到衰减，另外在实现上也比较简单，只要对边界区域的坐标变量参数进行设置就可以了，在实际的波传播区域完全可以不受影响，另外，使计算过程中采用并行运算成为可能。在实际的波传播区域，kx和kz等于1，同时σx和σz等于0。而在边界区域σx和σz大于0，这样可使电磁波在进入吸收边界区域后很快衰减。程序中，波的传播参数是按照以下原则设置的：

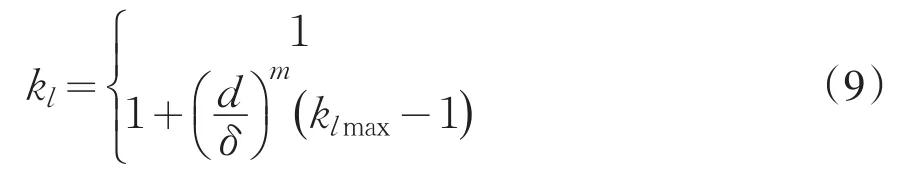
上面一行对应于波的传播区域，下面一行对应于波的吸收边界区域。

同理，将电导率σl设置为

从式（9）和（10）还可以看出，电磁波越深入边界层就会衰减得越快，这也是希望得到的结果。

2 探地雷达计算机仿真流程

探地雷达的计算机仿真过程其实是一个解一定边界条件下的麦克斯韦方程的过程。本文设计的整个仿真方法可以以图1所示的流程来表示。

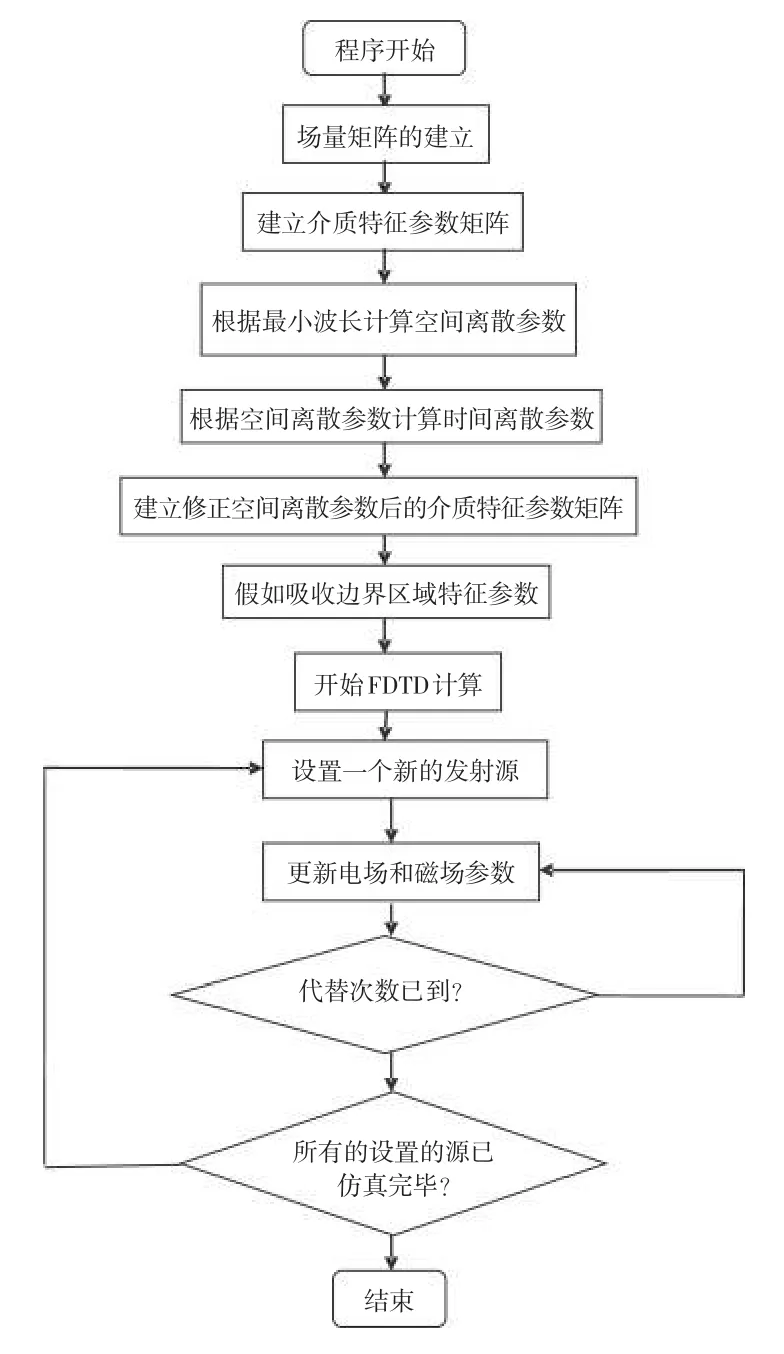
图1 探地雷达模拟计算过程Fig.1 Calculation process of the numerical simulation

3 计算模型与结果

3.1 计算模型的建立

图2中三个大小不同、埋于地下不同深度的黄色球状物是本研究中需要探测的三个目标对象。整个模型在纵向基本可以分成三层，Z＞0部分为空气层，本文对空气层设置的介电常数为ε0=1，磁导率为μ0=1以及电导率σ0=0。与空气接触的地下一层为介电常数为10的一种介质，地下第二层为介电常数为25的媒质。图中三个圆形物质从左到右分别为A、B、C，介电常数均为16，是本文需要探测的三个目标。为研究问题的简化，假定两种地下媒质的磁导率均为1，电导率为最上层的空气最小，而地下两层媒质与介电常数对应具有不同的电导率。这三层媒质用以表示探地雷达探测过程中遇到的基本地下结构。虽然这种结构有一定的理想化，但还是对实际地质结构的一种抽象，对进行探地雷达的正演模拟研究很有代表性，对研究探地雷达的探测机理具有十分重要的作用。图2描述了FDTD仿真的基本模型，以不同的颜色表示不同的介质特征参数。

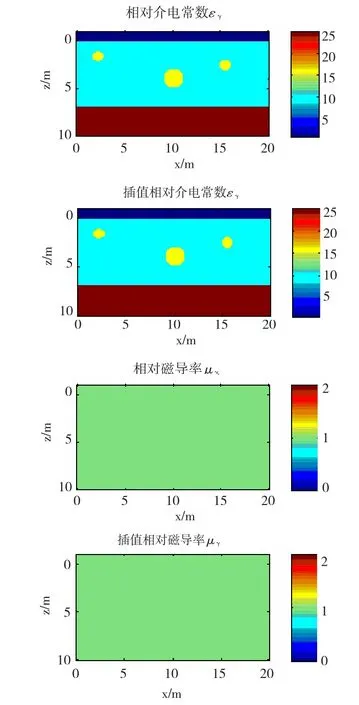
图2 探地雷达数值模拟的数学模型Fig.2 Numerical model for simulation of GPR

3.2 计算结果和分析

在探地雷达的发射源选择上，选用了Black-man-Harris脉冲源，在程序中通过将该一定频率的脉冲源加到电场E→y上来实现。在整个模拟计算过程中，所采用的电磁波频率为100 MHz。发射频率和波的形式对探测结果的影响将在下一阶段的研究中展开。

从图3可以看到电磁波的传播速度与介质特征参数之间的关系。在空气中电磁波的传播速度明显快于地下一层介质。在Z＞0部分的空气介质中，电磁波传播得很快，而在Z＜0的地下介质部分，电磁波的传播速度比较慢，这是由于地下介质的介电常数εr1大于空气中的介电常数ε0，而波的传播速度与媒质的介电常数的平方根成反比。

图3 不同媒质中波的传播速度Fig.3 Wave velocity in different medium

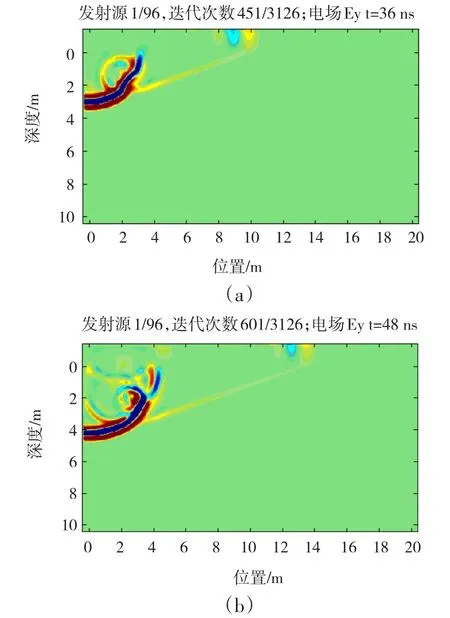
图4 目标物A的探测Fig.4 Detection of objective A

图4描述了当探地雷达的发射源位于坐标（1/96，0，0）位置时对目标对象A的探测过程。从图4（a）可以看到，当电磁波经过36 ns的传播后碰到了探测目标A，这时侯一部分波被目标对象A反射，另一部分波继续向前传播。发生反射的位置与图2探测模型中设置的目标对象A的位置基本一致。图4（b）描述了在图4（a）的基础上，电磁波继续向前传播12 ns后的电场Ey图。从图中可以看到，反射波经过一段时间的传播后已经衰减了很多，但前向波仍然继续传播。这说明反射波相对于透射波比较弱，在媒质中衰减得更快。从这三个图可以看到，正演计算模拟基本能够比较准确地探测到目标对象A，电磁波的波峰和波谷交替变化向前传播，当媒质特征（介电常数、磁导率、电导率）变化时会发生反射，反射波的产生与否可以作为判断是否有探测对象存在的依据。

图5描述了当探地雷达的发射源位于（41/96,0,0）时对目标对象B的探测过程。从图5（a）可以看到，当电磁波从波源开始传播过48 ns后，开始探测到目标对象B，因为这个时候开始，与图4一样有反射波的出现。而图4中反射波开始出现的时刻是在36 ns，这是由于目标对象B比目标对象A埋得更深，电磁波需要花费更多的时间才能传播到。从这个图中还可以看到，反射波出现的位置与图2模型中设置的目标对象B的位置基本一致，这进一步说明了模拟计算是有效的。图5（b）为电磁波继续传播4 ns后的场强图，可以明显看到波的传播，电磁波的传播速度很快。

图5 目标物B的探测Fig.5 Detection of objective B

4 结 语

本文利用MATLAB对探地雷达中电磁波的传播规律进行了计算机仿真并进行了详细的分析。从仿真结果可以看到，建立隐患模型的仿真方法是很有效的，水利工作者利用探地雷达进行大坝隐患探测工作的预测时可参考探讨的方法。

[1]Annan AP.GPR-history，trends and future developments[J].Subsurface Sensing Technologies and Applications,2002,3(4):253-270.

[2]葛德彪.电磁波时域有限差分方法[M].西安：西安电子科技大学出版社，2002：25-26.

[3]曾昭发，刘四新.探地雷达方法原理及应用[M].科学出版社，2006.

[4]李想堂，王端宜，张肖宁.探地雷达技术的回顾与展望[J].无损检测，2006，28（9）:479-483.

[5]Yee K S.Numerical solution of initial boundary value prob-lem involving Maxwell equations isotropicmedia[J].IEEE Trans.Antennas Propagat，May 1996,AP-14(3):302-307.

[6]Engquist B,Majda A.Absorbing boundary conditions for the numerical simulation of waves[J].Math.Comp.,1977,31:629-651.

[7]Daniels D J.A study of surface penetrating radar and its ap-plication[J].Microwave Jr,1994,37(2):68-82.