基于FPGA的FIR滤波器的误差分析

2011-06-13吴黎慧蒲南江高磊胡洋

电子测试 2011年8期

吴黎慧，蒲南江，高磊，胡洋

（中北大学信息与通信工程学院山西太原 030051）

0 引言

数字信号处理技术（digital signal processing，DSP）随着计算机和大规模集成电路技术的迅速发展，现已成为一项成熟的技术，其方法通常涉及变换、滤波、频谱分析、编码解码等处理。其中数字滤波是一个重要环节，它能满足滤波器对幅度和相位特性的严格要求，克服模拟滤波器所无法解决的电压和温度漂移以及噪声等问题。由于FIR滤波器只有零点、系统稳定等诸多优点使得其在工程上得到了广泛的应用。使用FPGA来实现FIR滤波器，既具有实时性，又有一定的灵活性。

1 FIR数字滤波器的设计

1.1 基本原理

有限脉冲相应（FIR）滤波器的系统函数为：

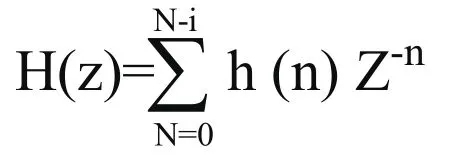
数字滤波器实际上是一个采用有限精度算法实现的线性时不变离散系统，它的设计步骤为先根据需要确定其性能指标，设计一个系统传递函数H（z）逼近所需要的技术指标，最后采用有限精度算法实现。

该系统的设计指标要求：采用窗函数法设计FIR低通滤波器；采样频率Fs为100Hz；截止频率Fc为30Hz；通带最大衰减为1dB；阻带最小衰减为40 dB。

常用窗函数的特性如表1所示，窗函数法的基本思想是使其具有最窄主瓣宽度和尽可能小的旁瓣。这种设计法的重点是如何选择合适的窗函数和理想滤波器。通过理论分析和对比，海明窗在6个窗函数中，主瓣宽度不是太宽8π/N，其最大旁瓣值比主瓣约低44dB，旁瓣抑制度高，普能量绝大部分集中于主瓣内，故选用海明窗用于滤波器的设计。用MATLAB提供的滤波器设计的专门工具箱FDATooL仿真设计滤波器，滤波器的幅频特性满足要求。把获得的滤波器系数导出为文本文件保存。

表1 5种窗函数基本参数比较

1.2 FPGA实现FIR滤波器

FPGA采用ALTERA公司生产的Cyclone III 系列中的EP1C6Q240C8芯片。使用滤波器描述编程，从而实现FIR滤波器的顶层原理图，如图1所示。

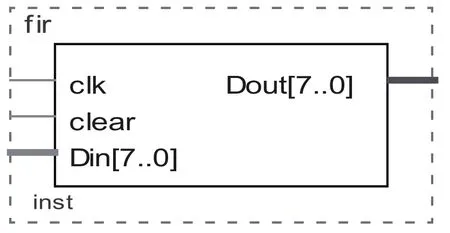
图1 滤波器顶层模块图

1.3 Quartus II 仿真结果

取输入信号Din=[99,0,0,0,70,0,0,0,99,0,0,0,70,0,0,0,99,0,0,0,70]，QuatusII仿真结果如图2所示，其中clear为复位信号，clk为时钟信号，Din为输入序列，Dout为输出序列。

1.4 MATLAB计算理论结果与仿真结果比较

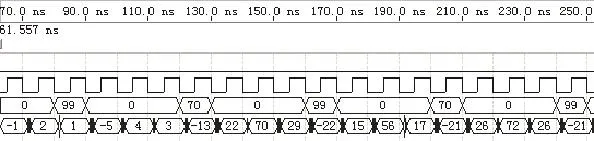
图2 FIR滤波器仿真结果

由滤波器卷积公式：

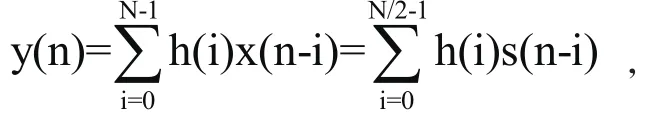
其中X(n)为输入序列用Din代替，系统函数为h(n)，详见表2.

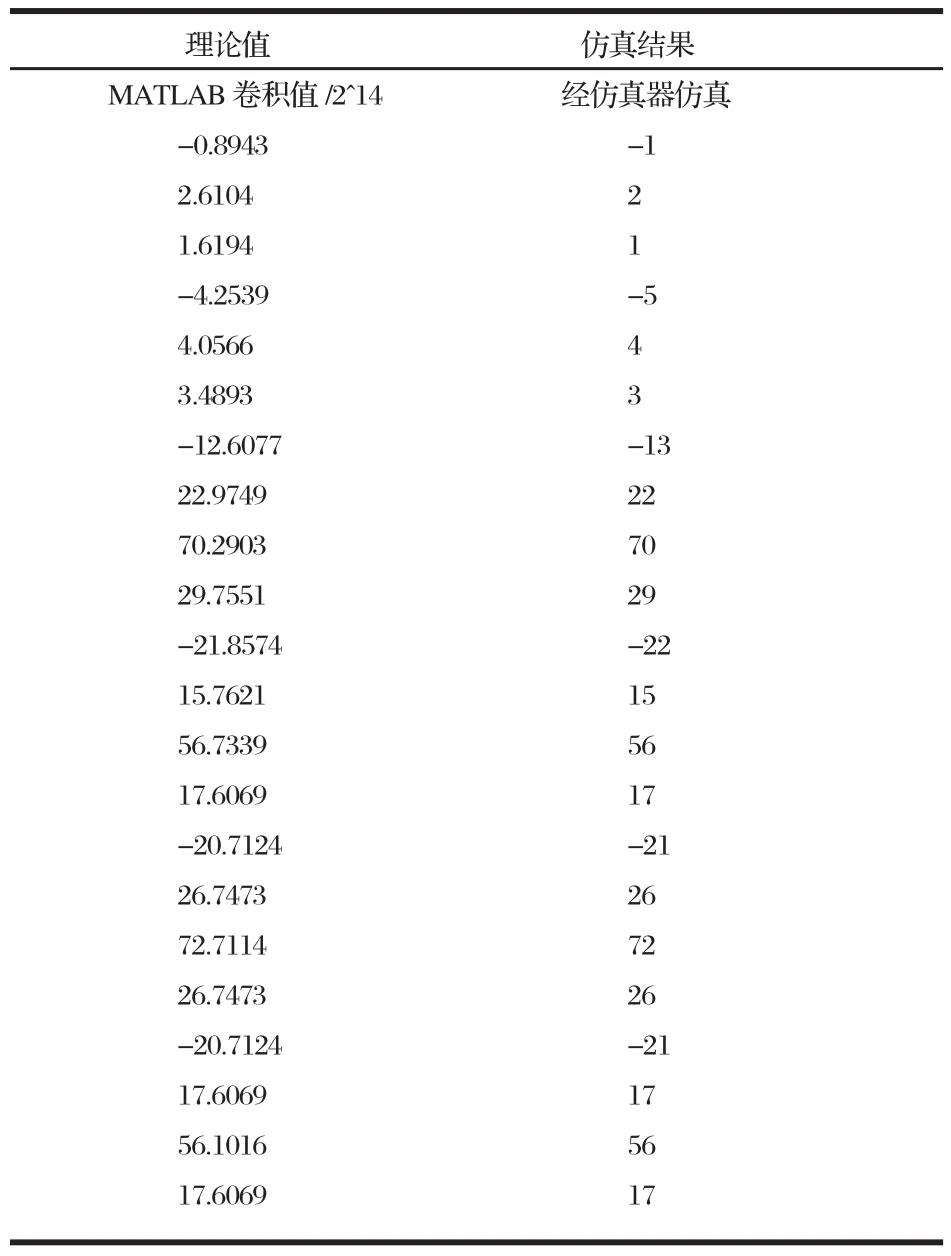
表2 FIR滤波器理论值与仿真结果比较

2 滤波器误差分析

量化系数后产生的滤波器频谱与理论滤波器频谱如图3所示。

通过图3可以发现，当把滤波器系数量化扩大2^14=16384倍时，设计的滤波器频谱与理论滤波器频谱非常接近，即此时的滤波器精确度较高。

2.1 绝对误差分析

把理论值与仿真值作差，通过MATLAB画图软件，得到绝对误差如图4所示。

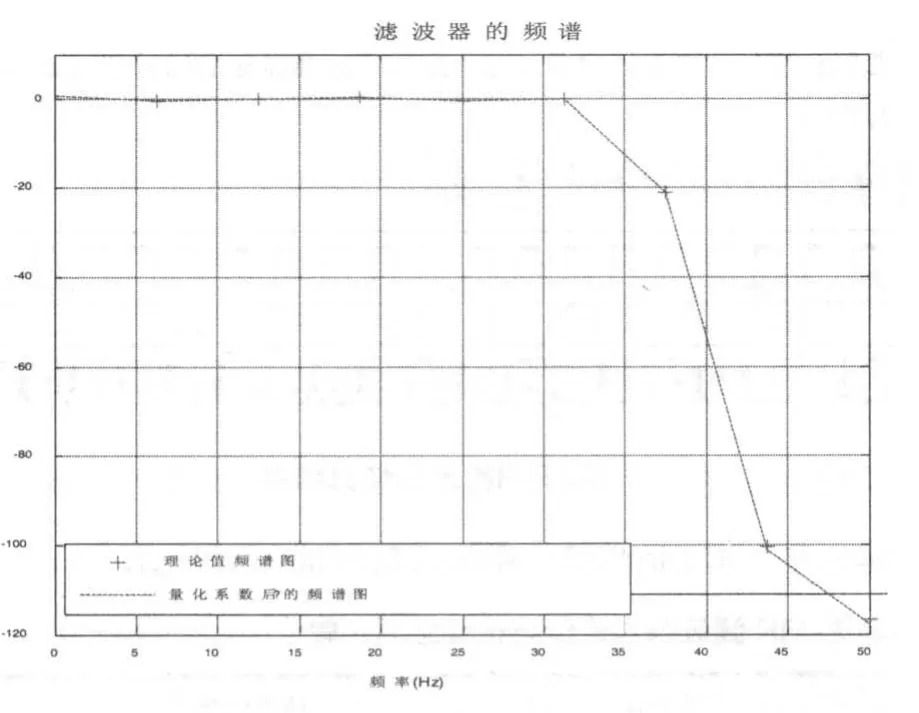
图3 频谱比较图

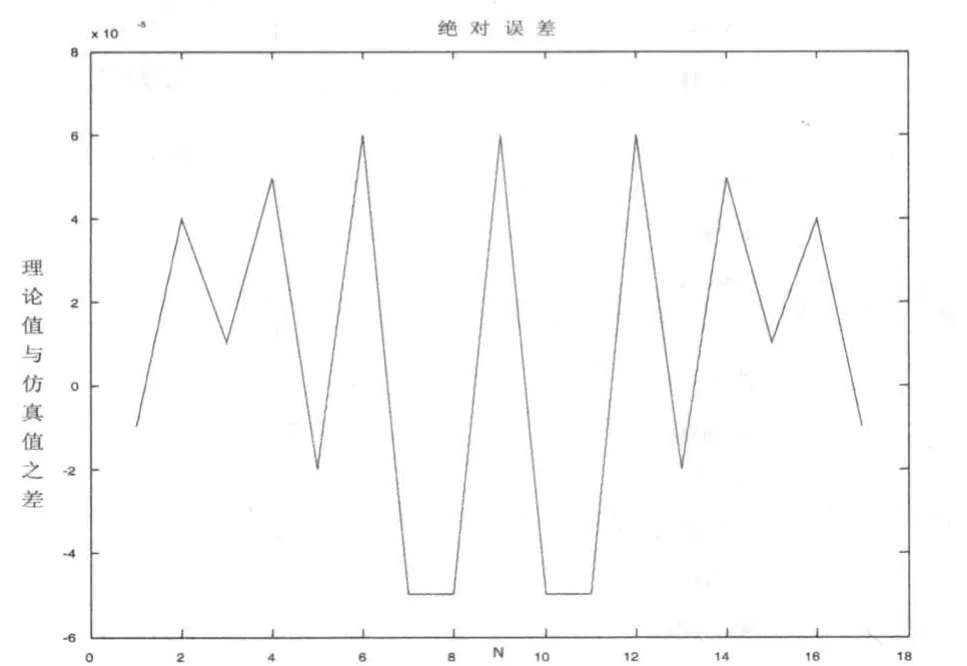
图4 绝对误差

由图4中得知其误差均值为x=7.5229e-005，方差p =1.8823e-008，可见，其误差均值和方差均非常小，在误差的允许范围之内，不会对工程结果产生严重误差。

2.2 相对误差分析

把理论值与仿真值作差后除以理论值就可得到相对误差，同样通过MATLAB画图软件得到相对误差的图样，如图5所示。

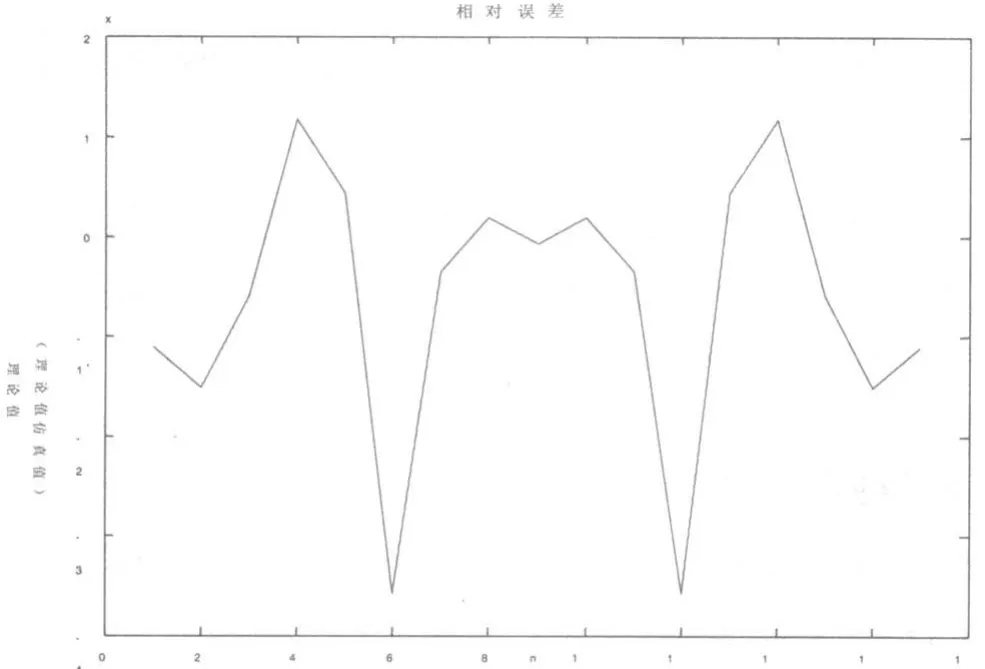
图5 滤波器相对误差

由图5可知为仿真滤波器相对误差,前几个结果相对误差相对较大，到n=6以后，相对误差基本可以维持在-0.1～+0.1的范围内，故在误差允许的范围内，采用FPGA设计的滤波器与MATLAB理论仿真的结果完全吻合，此种方法完全可行。要想得到比较精确的结果，可以适当提高滤波器系数扩大的倍数，但这是以提高资源占用大小为前提的。