固结和蠕变耦合作用软土深基坑变形性状研究

王继荣 陈建永 王春雷

0 引言

开挖问题与岩土工程中其他问题的主要区别在于土方开挖使坑底土体应力处于释放状态，由于卸荷而在坑底土体中产生超静负孔压。另外，挖方通常是分层、分阶段进行的，施工过程和边界条件的改变使问题的研究更加复杂。

在软粘土地基中进行的深开挖工程具有时间效应。开挖期间基坑性状的改变是由开挖卸荷所致，而开挖间歇期内的变化一般是由于土体的固结和蠕变所引起的。本文所要研究的是土体的固结及蠕变对基坑开挖的影响。

1 软土的固结理论

1.1 比奥(Biot)固结理论

无论是单向还是准三维固结理论，都只研究了土体中超静孔压的消散过程，并没有涉及到与位移场的耦合作用。为了能将土骨架变形和孔隙水渗透(或孔压消散)同时考虑，1941年，Biot做了如下假定:

1)土体是均质的，完全饱和;2)土粒和孔隙水为不可压缩介质;3)除渗透性之外，土体是各向同性线弹体，压缩系数恒定;4)土体内孔隙水服从Darcy定律，渗透系数保持恒定;5)土体的变形是微小的;6)不计惯性力和体积力。

基于土体平衡方程、本构方程、几何方程、有效应力原理、Darcy定律、渗流连续方程推导了真正意义上的真三维固结方程:

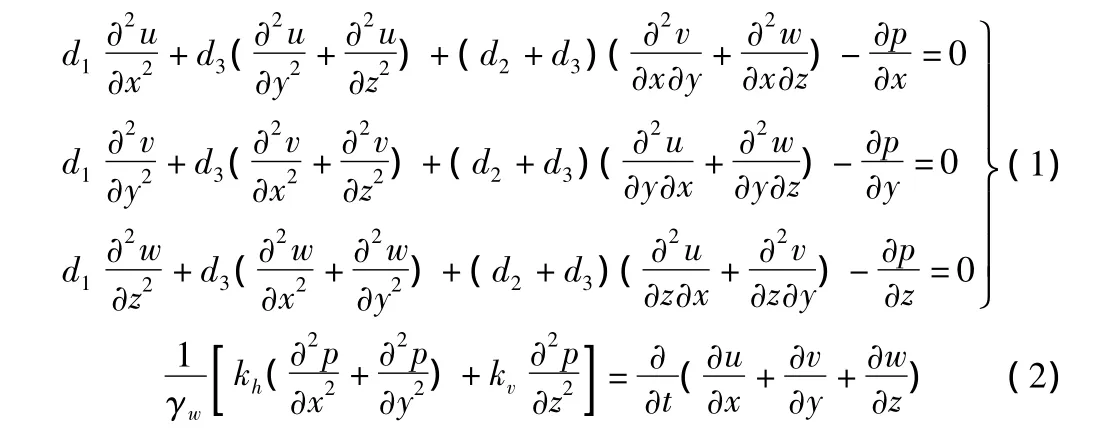
方程式(1)和式(2)即为Biot三维静力固结方程，也是有效应力(静力)分析法的控制方程。

Biot是从比较严格的固结机理出发推导的三维固结方程，其准确反映了孔压消散与土骨架变形相互耦合关系。

1.2 Biot三维固结问题有限元法求解过程

Biot三维固结有限元方程的推导可分为两步:先对Biot三维固结方程进行空间离散，然后再进行时间离散。现进一步对用有限元法求解三维固结问题的整个过程作一简单描述:

1)空间和时间离散;2)固结有限元方程的整体组装;3)引入边界条件;4)求解线性方程组;5)计算当前节点位移和孔压;6)计算节点应力;7)时段循环。

1.3 比奥(Biot)固结理论的推广

Biot固结理论是针对线弹性土体建立起来的，但也可以推广应用于建立在非线性基础上的粘弹塑性。Biot固结理论中力的平衡方程、体积变化连续性方程，均与土的应力—应变关系无直接联系，故无需作任何变动即可应用于饱和流变土体的固结问题。

Biot粘弹塑性固结理论中力学平衡方程、物理方程、几何方程及体积变化连续性方程分别表示为:

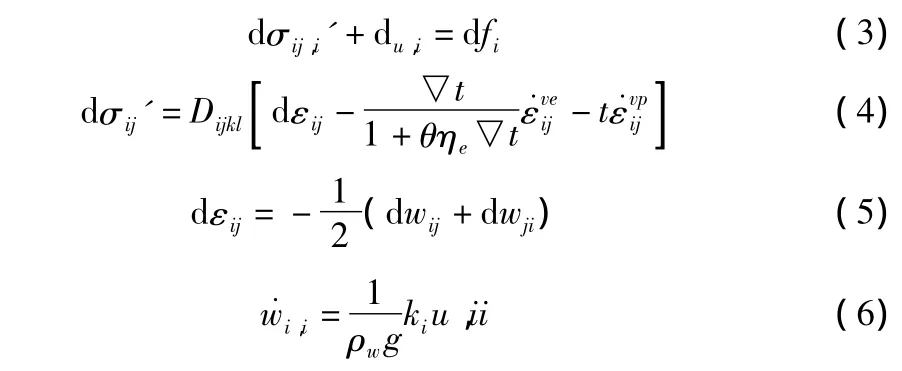
其中，εij为瞬时弹性应变;dσij'为有效应力的偏导;u，i为角标，含义为对平面坐标的依次偏导;fi为体积力;Dijkl为土体本构关系中的应力—应变关系矩阵;θηe为模型参数;w˙i，i为位移对坐标偏导再对时间偏导;ρw为水的比重;ki为渗透系数;u，ii为孔压对时间的二阶偏导为粘弹性应变速率为粘塑性应变速率。

由以上四式，给以初始条件和边界条件，便可进行有限元等数值求解。求解步骤如下:

1)由基本方程(3)～方程(6)解得孔隙水压力、位移增量、应力增量及总应变增量;2)求得粘弹性应变增量，叠加求得累积粘弹性应变;3)求得粘塑性应变增量，叠加求得累积粘塑性应变，粘弹性应变速率、粘塑性应变速率;4)对新的时间增量(步长)，重复以上步骤，直至固结结束。

2 工程算例

某基坑宽40 m，深10 m，采用地下连续墙支挡，设两道水平支撑，其中心分别位于地表下2.0 m和6.0 m。土体、支撑和地下连续墙的参数如表1，表2所示。假定地下水位线位于地表，并在基坑的远端水的补给充足，土体的水平和竖向渗透系数分别为2e－7 m/s和3.5e－7 m/s。土体采用扩展的D—P蠕变模型，蠕变参数 A，n，m 分别取为:9.42e －9，1，－0.9378。土体单元采用耦合的CPE4P单元。围护墙采用实体单元CPE4R，支撑采用杆单元T2D2。边界条件为:计算域左右两侧水平位移均约束，底面水平、竖直方向均约束，以上边界均为不透水边界，每步开挖结束后基坑底面孔压为零。

表1 土层的力学参数

表2 支撑和地下连续墙的力学参数

分步开挖和施工间歇的具体实施步骤如下:

1)施加重力荷载，对模型进行一次静力分析，导出模型应力数据作为输入文件，在初始状态输入文件得到地应力的平衡;

2)第一次开挖至地表下3 m处，设置第一道支撑，时间共5 d，*soil Consolidation分析步;

3)间歇3 d，*soil Consolidation分析步;

4)第二次开挖至地表下8 m处，设置第二道支撑，时间共8 d，*soil Consolidation分析步;

5)间歇4 d，*soil Consolidation分析步;

6)进行第三次开挖至地表下10 m处，时间共4 d，*soil Consolidation分析步;

7)间歇18 d，*soil Consolidation分析步;

8)在开挖过程中，定义弹性模量随温度变化，温度为0，1和2时，土的弹性模量分别为 6e3MPa，2.4e3MPa 和 0.96e3MPa，以达到模拟逐步开挖的过程。

3 有限元分析结果及讨论

3.1 蠕变与固结耦合作用对支撑轴力及墙体水平位移的影响

图1为开挖后基坑支撑轴力随时间的变化情况，表3为不同时间墙体水平位移最大值的变化情况。图2为开挖结束后墙体变形情况。分析图1，图2可以得到以下结论:

1)第一道支撑轴力随时间的增长而减小，可以看到刚开始几天几乎保持不变;2)第二道支撑轴力先减小后增大;14 d后，第一道或第二道支撑轴力变化率趋于稳定;3)考虑耦合作用时，由于负超静孔隙水压力的消散，刚开始墙体水平位移最大值减小，随着时间增加，土体蠕变导致墙体变形变大，这说明到后期土体的蠕变作用占据主导地位。

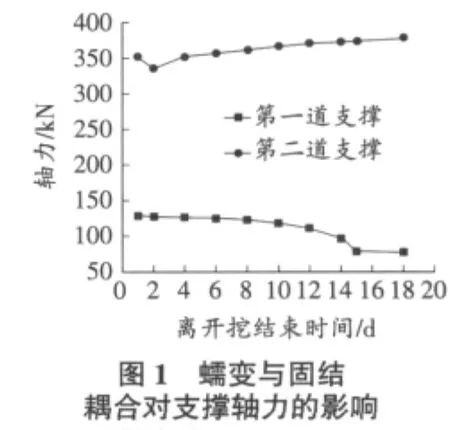
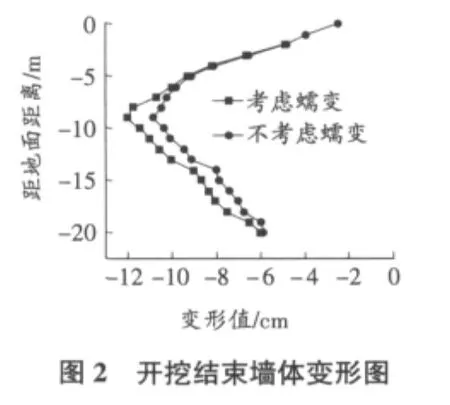
表3 不同时间墙体水平位移最大值

3.2 分块开挖及施工间歇长短对基坑变形的影响

针对以上的算例，对不同施工参数条件下的基坑开挖进行分析。主要改变开挖方式，使用盆式分块开挖。先分层开挖，每层先开挖中间10 m宽的土体，然后再开挖两侧土体，每层开挖的总时间与整体开挖的时间相同。而施工间歇期研究分为三种情况:

1)把施工间歇期统一延长为10 d;2)保持原施工间歇期不变;3)取消施工间歇期。研究施工间歇期长短对围护结构变形的影响。

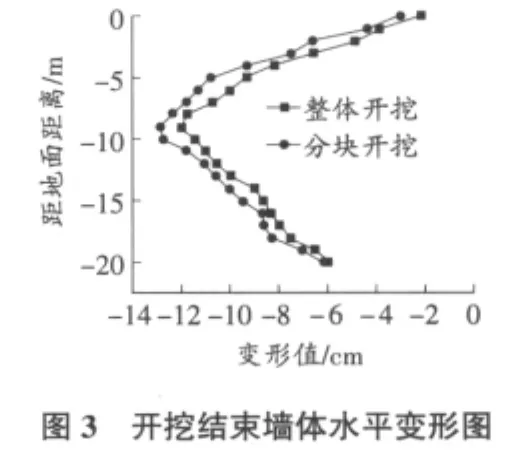
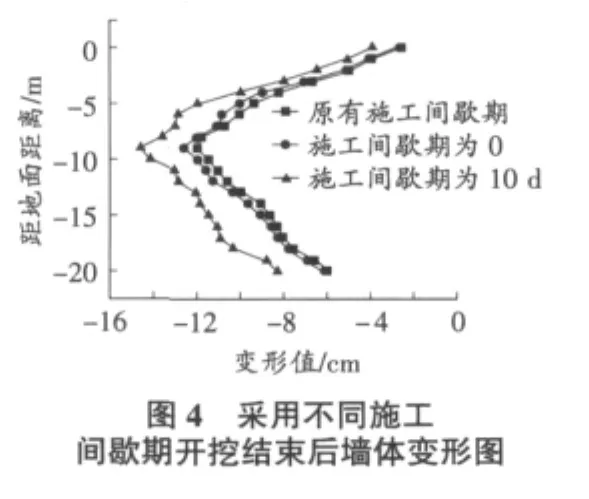
图3给出开挖结束后墙体变形情况，图4为开挖结束后墙体的变形图。从中可得出以下结论:

1)坑周土体在开挖过程中的变形与施工参数密切相关;

2)采用分块开挖和采用整体开挖得到不同的结果，采用分块开挖的墙体水平位移比采用整体开挖的小;

3)产生此类现象的原因是:中间的土方被挖除，基坑内侧剩余的土体对墙体的变形起抵抗作用，而开挖的时间不变，所以墙体的变形较整体开挖的小;

4)在一定的条件下采用优化的施工参数和施工工艺对控制地层移动效果比较显著;

5)取消施工间歇期情况下，围护墙体的变形增大。可以认为是土体固结尚未完全发生作用。在合理施工间歇期，由于负的超静孔隙水压力的消散，坑内外水头差的减小，墙体水平位移最大值将逐渐减小。可见保留合理的施工间歇期对保持基坑稳定有利;

6)在增大施工间歇期情况下，围护墙体的变形大幅增加。这说明随着施工间歇期的增加，土体的蠕变占据主导地位;

7)合理的施工间歇期应与土体的渗透系数、开挖土方的大小、开挖时间长短等因素有关。

4 结语

本文简单介绍了比奥(Biot)固结理论及其有限元解法，并对该理论进行了推广，使其可以考虑土体的蠕变效应。基坑的时间效应是土体固结和蠕变共同作用的结果。应用大型有限元软件ABAQUS对工程算例进行有限元分析。分析中考虑了土体固结及蠕变的耦合作用。由工程算例分析可知，在深基坑变形计算中，有必要考虑土体蠕变和固结耦合作用，而且考虑土体蠕变和固结耦合作用后得出的结果更接近于工程实际。

［1］ 吴兴龙，朱碧堂.深基坑开挖坑周土体变形时空效应初探［J］.土工基础，1999，3(13):5-7.

［2］ 孙 均.岩土材料流变及其工程应用［M］.北京:建筑工业出版社，1999.

［3］ 高文华，杨林德.软土深基坑围护结构变形的三维有限元分析［J］.工程力学，2000，10(2):134-141.

［4］ 陈晓平.软土变形时效特性的试验研究［J］.岩石力学与工程学报，2005，24(12):2143-2149.