非均匀层状地基的应力和位移场分析★

陈金光 黄永强

0 引言

随着我国基本建设的快速发展，高层建筑和对地基有特殊要求的建筑物日益增多，在基础工程设计与施工方面积累了不少成功的经验。但也有不少失败的教训，例如上海展览中心馆、北京大学汽轮机基座等造成了大量的损失和重复施工。这些事例充分表明，对基础工程必须慎重对待。基于前人大量的研究成果，针对非均匀地基，建议了一种基于层状材料Kelvin基本解的数值方法，并计算了均匀地基和非均匀地基在圆形荷载作用下的应力和位移场，为工程应用提供了参考。

1 基于广义Kelvin基本解的层状地基的分析方法

1.1 层状材料广义Kelvin基本解

下面概述一下层状材料的广义Kelvin基本解［1］，详细的推导和分析可在原文中找到。广义Kelvin基本解是关于无限域层状材料中集中荷载作用下的位移和应力场。无限域中，材料的层数为任意数，层状材料上下分别与半无限均匀介质完全粘结。任何连接在一起的层状材料的交界面为完全粘结。该基本解一个显著的特点是:对于层数任意的层状材料，能获得闭合解，且具有很高的计算精度。

1.2 求解非均匀地基应力位移场的基本方程

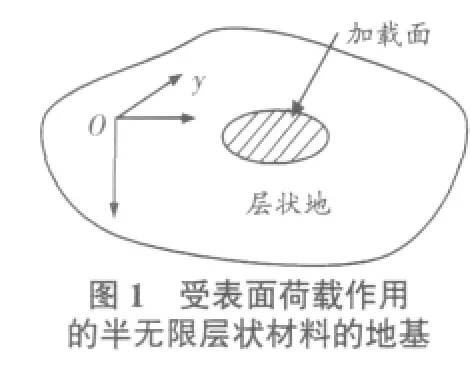
对于非均匀地基，可以采用广义Kelvin基本解来分析。可以假设第0层的弹性模量为一很小的值，比如E0=1×10－15MPa。这样就可以采用类似Mindlin解分析半无限域的方法来分析非均匀地基的情形，如图1所示。

半无限域内非均匀地基任意一点的应力可由下式计算:

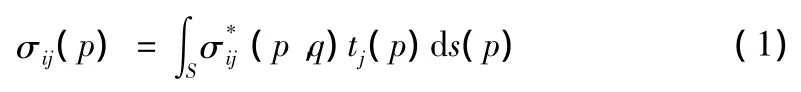
半无限域内非均匀地基任意一点的位移可由下式计算:

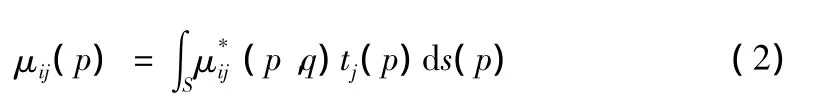
如果加载区域S不规则或荷载不均匀，不能采用简单的积分办法。可采用类似边界元离散的方法求解，可将整个加载区域S离散成m个单元，则:

采用8节点等参单元，并引入起插值函数，则半无限域内任意一点在整体坐标下的位移可用局部坐标系表示为:

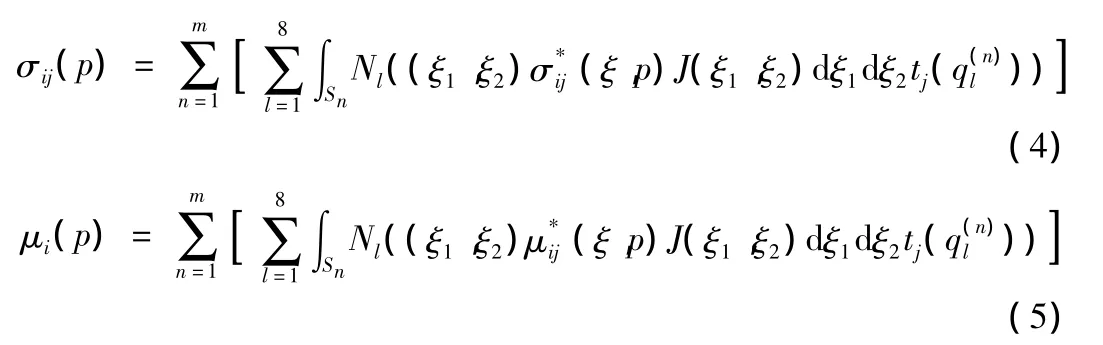
其中，n为第n个单元;l为等参单元的第l个节点;N为等参单元的差值函数;ξ为局部坐标矢量;J为雅可比矩阵。

2 均布荷载作用下均匀地基算例验证

2.1 计算模型建立

下面利用编写的Fortran程序，分析一个存在已知解的例子，以验证本文计算方法的精确性。

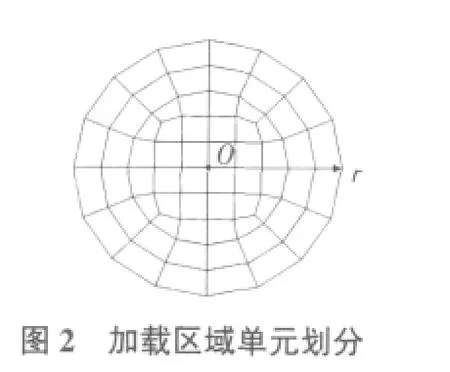
图2为圆形加载区域的单元划分及部分边界计算节点，共划分了64个单元，209个节点，半径为100cm，其上作用着大小为fz=1.0MPa的均布荷载，其弹性模量为 E=850 kg/cm2，泊松比μ =0.25。

计算过程中，沿r轴共取了35个边界点，每个边界点正下方对应着5个计算节点。图2中每一条曲线表示每一个深度上各计算节点的应力或位移值。

2.2 数值解与理论解之误差分析

竖向位移ur(r=0处)利用本文方法所求出的数值解与参考文献［3］［4］的理论值所作的对比，并且计算了其相对误差，其中最小误差2.00376%，出现在z=10cm处;最大误差为3.23616%，出现在z=300cm处。

竖向应力σz的数值解与参考文献［4］中理论值的对比，其中最小误差为0.01824%，出现在r=0，深度z=900cm处;最大误差为11.5693%，出现在r=120cm，深度z=10cm处。整体上看，相对误差主要集中在1.0%～4.0%之间。

径向应力σr的数值解与参考文献［3］［4］的理论值的对比，其最小误差为0.00422%，出现在r=40cm，z=70cm处;最大误差为9.7561%，出现在r=100cm，z=70cm处。

2.3 应力与位移数值解曲线图

由图3可知，σz值在加载边界(r=1 m)处发生突变，其数值在圆形加载区域内部随深度的增加而逐渐减小;在圆形加载区域外，σz应力值随深度的增加而增加;从径向看，σz值从圆心处沿径向减小，在r=200cm处曲线走势开始平缓并逐渐趋于0。

竖向位移uz的数值曲线基本与竖向应力σz的数值曲线走势相同(见图4)。其值随深度的增加而减小并逐渐趋于0。

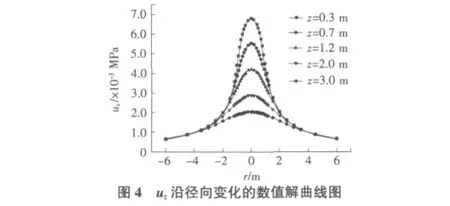
图5形象的反映了随深度变化σr值的变化规律。在加载边界(r=1 m)附近，曲线出现拐点。随着深度的增加，圆形区域内的σr值越来越小，r=0处σr值的变化速率较快。从径向看，当一定的深度，圆形r=0处的σr值最大，沿径向逐渐减小，在加载区域边界迅速较小，之后曲线走势平缓;随深度的进一步增大，圆心处的σr值开始小于附近区域的σr值，在加载区域边界σr值达到最大，随后σr值沿径向逐渐减小。深度z=70cm处的σr曲线形象的反映了随深度增加，σr值沿径向的变化规律。

通过上述三曲线我们可以发现，在圆形加载边界(r=1 m)处，应力和位移发生突变，加载区域边界是曲线变化与走势的分界点。

3 圆形荷载下非均匀地基应力和位移场分析

某一地层情况如下:第一层厚h1=100cm，弹性模量E1=687 kg/cm2，泊松比 v1=0.3;第二层厚 h2=75cm，E2=845 kg/cm2，v2=0.35;第三层 h3=125cm，E3=961 kg/cm2，v3=0.35。其上作用着圆形均布荷载Fz=1MPa，荷载半径r=100cm。

计算过程中沿径向取了r=0cm，50cm，100cm，150cm，200cm，250cm，计算了各深度处的 uz，σz，σr值，以期发现对工程有指导作用的信息。

从图6可以看出，竖向位移uz随深度的增加逐渐减小，曲线变化趋势基本与均匀地基的情况相似;从径向看，在荷载区域，位移值沿径向逐渐减小，在加载区域内，位移值区间较大，在加载区域边界处，曲线的走势开始变化，位移值区间缩小。

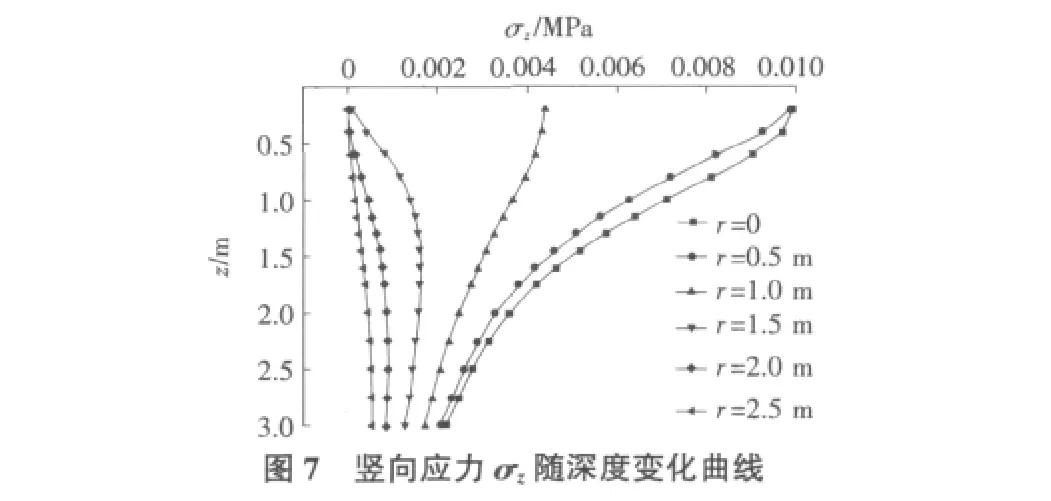
从图7可以看出，竖向应力σz在加载区域内，随深度的增加而减小;在加载区域外，随深度的增加而先增大后减小。另外，应力值沿径向逐渐减小，在加载边界r=100cm，应力值在径向产生突变。

从图8中可以看到，在层与层的分界面(z=1.0 m和z=1.75 m)上，径向(水平)应力值σr将发生明显的跳跃现象。在边坡工程上应该考虑应力值在水平方向的突然跳跃，尤其对于多层夯实高路堤或土边坡，水平方向应力值在层间的跳跃现象可能成为影响稳定性的因素。

4 结语

由以上计算分析可见，用本文的计算方法所得出的结果与理论值之间的误差可以被控制在一个较小的范围内。采用基于层状材料基本解，在整个加载面上积分来计算给定点的位移和应力，这种方法可以较精确的计算数值解。本文用该计算方法仅计算了圆形荷载的应力和位移分布情况，复杂荷载和复杂边界下的应力和位移也可以由本文的计算方法得到。

对于层状地基，竖向的应力和位移值的变化趋势与均匀地基的情况相似，但水平方向的应力值受到层状特性的影响。在边坡等工程上应该考虑应力值在水平方向的突然跳跃，尤其对于多层夯实高路堤或土边坡，水平方向应力值在层间的跳跃现象可能成为影响稳定性的因素。

［1］ Yue Z Q.On generalized Kelvin solutions in multilayered elastic medium［J］.Journal of Elasticity，1995(40):1-43.

［2］ 王焕定，焦兆平.有限单元法基础［M］.北京:高等教育出版社，2002:117-120.

［3］ Poulos HG，Davis EH.岩土力学弹性解［M］.孙幼兰，译.北京:中国矿业大学出版社，1986:60-79.

［4］ 赵明华.土力学与基础工程［M］.武汉:武汉理工大学出版社，2008:50-56.