基于属性加权的朴素贝叶斯分类算法改进

刘牛

安徽工业大学计算机学院 安徽 243032

0 前言

分类是数据挖掘中一项重要的核心技术，其目的就是通过学习得到一个目标函数f，把每个属性集映射到一个预先定义的类标号y，因此可以将分类看作是从数据库到一组类别的映射。这些类别是被预先定义的，没有重合的。数据库里的每一个元组都可以准确地分配到某个类中。朴素贝叶斯分类器是一种最简单、有效、具有坚实的理论基础并在实际应用中得到广泛使用的分类器。朴素贝叶斯分类方法基于条件独立性假设，即假设一个属性对给定类的影响独立于其他属性，而这在现实问题中往往并不成立，为此，许多学者做了大量的工作来放松独立性假设。Harry Zhang等根据条件属性对决策所起的作用给予它们不同的权值，提出了加权朴素贝叶斯分类模型。Zhou Jiyi等根据粗糙集权重确定方法提出了一种基于区分矩阵的属性权重确定法。程克非、张聪提出了一种基于特征加权的朴素贝叶斯分类器。秦锋、任诗流提出一种通过用加权调整的先验概念来代替原朴素贝叶斯的先验概率。白似雪，梅君提出一种计算每个属性对每个类的相关概率和不相关概率，并以此进行加权。本文提出另一种加权方法，将信息论里互信息知识与属性之间的相关性相结合，给予不同的条件属性赋予不同的权值，实验证明，这种方法能有效提高分类效果。

1 朴素贝叶斯分类器

每个元组用一个n维属性向量X= {x1,x2,…xn}表示，描述由n个属性A1, A2，…，An对元组的n个测量。假定有m个类C1,C2.. .,Cm。这样，给定一个未知的元组X，其P(Ci|X)最大的类Ci称为最大后验假定。根据贝叶斯定理：

由于P(X)对于所有类为常数，只需要P(X|Ci)P(Ci) 最大即可。如果类的先验概率未知，则通常假定这些类是等概率的，即P(C1) =P(C2) = . . .P(Cm)。并据此对P(Ci|X)最大化。否则，最大化P(X|Ci)P(Ci) 。注意，类的先验概率可以用P(Ci) =si/s计算其中si是类Ci中的训练样本数，而 s 是训练样本总数。

给定具有许多属性的数据集，计算P(X|Ci) 的开销可能非常大。为降低计算P(X|Ci) 的开销，可以做类条件独立的朴素假定。给定元组的类标号，假定属性值有条件地相互独立，即在属性间不存在依赖关系。这样，

先验概率 p(x1|Ci)，p(x2| Ci)，……，p(xn|Ci)可以从训练数据集求得。

根据此方法，对一个未知类别的样本X，可以先分别计算出X属于每一个类别Ci的概率P(X|Ci)P(Ci)，然后选择其中概率最大的类别作为其类别。即朴素贝叶斯分类模型为：

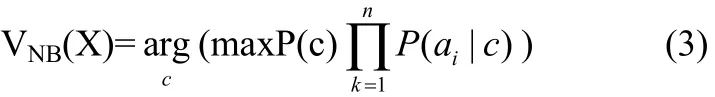
2 属性加权朴素贝叶斯分类算法

在现实实际应用中不同的条件属性与决策属性之间的相关程度是不同的，当条件属性与决策属性的相关程度高，它对分类的影响就要更大些，反之，如果条件属性与决策属性的相关程度较小，那么它对分类的影响就会很小。条件属性与决策属性的相关关系可以用相关系数的求解公式求得。设条件属性为 Xi，决策属性为 Y，其相关系数可以通过 Xi与Y的协方差与Xi与Y的方差的几何平均数求商得到，它反映了Xi与Y属性的线性相关紧密的程度，值越大表明属性之间的联系越紧密，反之则联系较差。

属性间的相关系数为：

由于权值的范围介于0和1之间，则设定权值为：

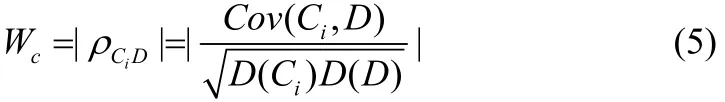
信息论里的互信息概念是描述某个随机变量关于其他随机变量变化时的信息量的大小，它可以用来反映条件属性提供的关于决策属性的信息量的大小。而相关系数是通过代数方法里的协方差与方差来求得的，它侧重与属性间的偏离程度，能够有效的改进分类能力，但是它对属性间的变化不敏感。因此希望通过结合相关系数与互信息的知识，从而使属性获得更好的权重，提高分类效果。

设条件属性C和决策属性D的互信息，记为：因此可以得出条件属性i C的权值为：

综合相关系数与互信息的权值公式，定义两者的平均值作为新的权值公式：

基于属性加权的AWI-AUC算法的实现关键在于求出各条件属性与决策属性之间的相关系数和他们的互信息。具体算法步骤如下：

步骤1 数据预处理：将训练样本和待分类样本进行补齐和离散化；

步骤2 分类器的建构。

步骤2.1 读入并搅乱数据集，对数据集里的条件属性，决策属性，以及训练样例进行统计，生成统计表。再将数据集划分为新的训练集和测试集。

步骤2.2 生成分类器网络结构，并对其进行参数学习。

步骤2.3 计算所有的先验概率值，即在决策属性Dj下各个条件属性Ci取值的概率p(Ci|D)。

步骤3 计算权值。

步骤 3 .1 权值 Wc的计算。扫描所有的训练集，求出各条件属性与决策属性的协方差 Cov(Ci，D)和方差 D(Ci)和D(D)，通过公式计算得到相关系数ρCiD，则权重Wc= |ρCiD|。

步骤 3 .2 权值 Wi的计算。先求出条件属性和决策属性的互信息I(Ci,D)，再计算权重Wi。

步骤3.3 综合权值Wc和Wi，求得所需的权值Wci，并生成属性权值列表。

步骤4 分类评估。通过对属性给予不同的权值，得出分类结果。

该算法的性能在各多项式时间内完成，并且算法可行。

3 实验结果及分析

为了验证算法的可行性和有效性，用数据集对算法进行了测试。实验数据集选自UCI(University of California in Irvine)数据库，下载网址是 http：//www.ics.uci.edu/～mlearn/ MLRepository.html。所有数据集中数据的连续属性值均进行离散化处理。实验在MBNC(Bayesian Networks Classifier using Matlab)平台下完成。首先对数据集进行随机搅乱，打乱数据之间原先的排列顺序，并对数据集采取5叠交叉验证。每个数据集轮流实验5次，取5次实验的平均值作为实验的测试结果。表1为经过预处理后的数据集情况。

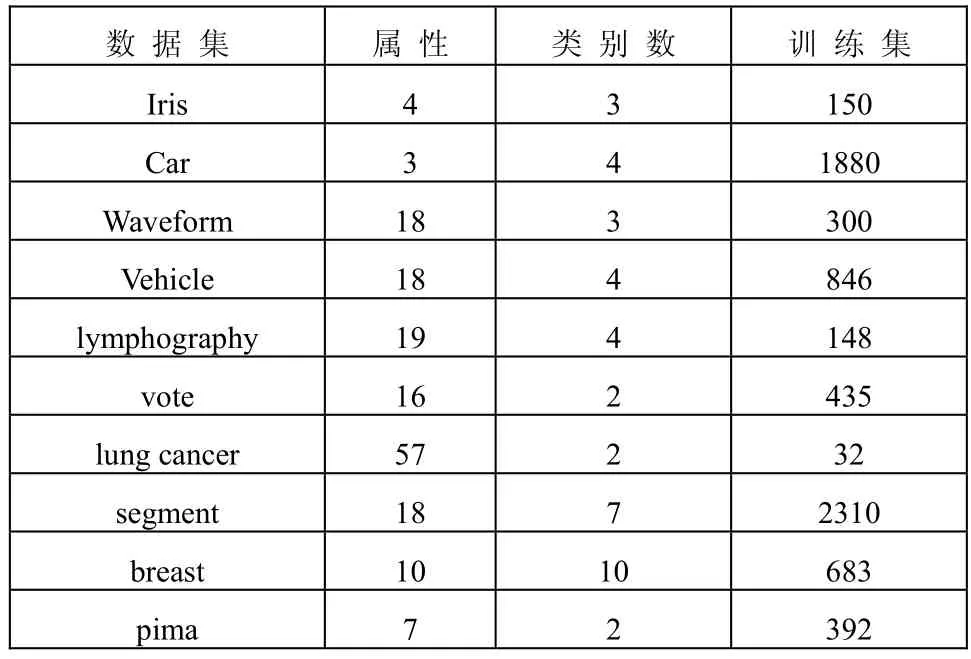
表1 预处理后的数据集

实验结果如表2所示。O-AUC表示的是没有使用加权方法时得出的AUC值，CC-AUC表示的是使用相关系数作为加权方法得到的AUC值，I-AUC表示的是使用信息论中的互信息知识作为权重后得到的AUC值，AWI-AUC表示的是本文提出的AWI-AUC算法得到的AUC值。

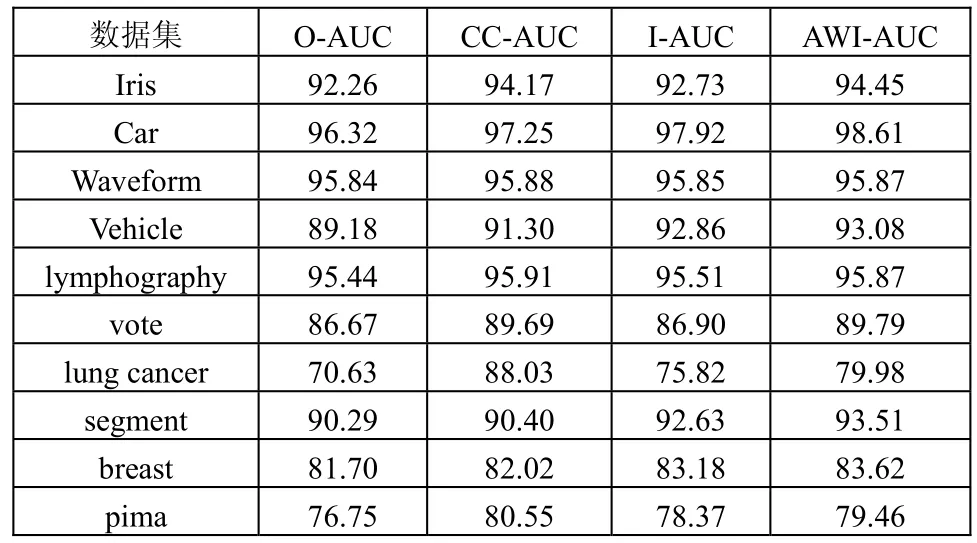
表2 实验数据结果

由表2可知：

(1) 当 O-AUC与 CC-AUC，I-AUC比较时，可以看出CC-AUC，I-AUC在各个数据集下得到的 AUC值均大于O-AUC，可见通过把条件属性与决策属性的相关系数和互信息作为条件属性的权重，可以提高分类器的分类性能，使得分类更加准确。

(2) 当 CC-AUC与 I-AUC比较时，CC-AUC的值比I-AUC的值大的有6个数据集，比I-AUC值小的有4个数据集，并且这4个数据集中的训练集个数均偏大，可见I-AUC更适合对数据集大的进行分类，会获得更好的分类效果，只是原样本集里填充和离散的数据会对原样本产生影响。CC-AUC在这种情况下可以有效地提高贝叶斯分类能力。但CC-AUC采用的权重是通过相关系数得到，相关系数由代数的计算方法求得，结合实验对数据规模偏小的数据集更加适合，因此将上述两种方法综合求均值，得到新的 AWI-AUC方法，通过实验证明AWI-AUC在总体上要好于其他方法，并证明了通过挖掘属性之间的潜在关系，对属性赋予不同程度的权重，可以获得更好的分类效果。

4 结束语

本文基于研究条件属性与决策属性之间的关系，并结合信息论中互信息的相关知识，提出一种加权的AWI-AUC方法，根据条件属性对决策分类的重要性不同给予其不同的权重系数来对AUC方法进行优化评估。在MBNC实验平台上实现该方法，并在数据集上通过实验比较，表明该方法的有效性和可行性。今后，将进一步研究改进条件属性与决策属性相关性的方法，以及分析条件属性与条件属性之间的关系，是否能够更好地提高分类器的分类能力。

[1]秦锋,杨波,程泽凯.分类器性能评价标准研究[J].计算机技术与发展.2006.

[2]Harry Zhang, Shengli Sheng. Learning Weighted Naïve Bayes with Accurate Ranking. [C] // The 4th IEEE International Conference on Data Mining.Chicago: IEEE Computer Society,2004.

[3]ZHOU Jiyi, LV Yuejin. A New Method of Ascertaining Attribute Weight Based on Discernibility Matrix.CSIST.2010.

[4]程克非,张聪.基于特征加权的朴素贝叶斯分类器[J].计算机仿真.2006.

[5]秦锋,任诗流等.基于属性加权的朴素贝叶斯分类算法[J].计算机工程与应用.2008.

[6]白似雪,梅君,吴穹.一种基于概率加权的朴素贝叶斯分类.2009.

[7]林士敏,王双成,陆玉昌.Bayesian 方法的计算学习机制和问题求解[J].清华大学学报.2000.

[8]张明卫,王波,张斌.基于相关系数的加权朴素贝叶斯分类算法[J].东北大学学报(自然科学版).2008.

[9]C.Blake and C.Merz, UCI Repository of Machine Learning Databases. http:// www.ics.uci.edu/～mlearn/ MLRepository.html.1998.

[10]程泽凯,林士敏,陆玉昌.基于 Matlab的贝叶斯分类器平台MBNC[J].复旦学报.2004.