关联规则挖掘在教师成长中的应用

2011-06-12高晓红柴银平

网络安全技术与应用 2011年6期

高晓红柴银平

楚雄师范学院云南 675000

0 引言

随着现在信息技术与科技的发展，现代高校在引进许多新技术和设备的同时也积累了许多教师的数据。并形成了具有一定规模的教师信息数据库。然而面对众多的数据，高校管理层如何利用，如何从中发现对高校教师队伍建设有实际指导意义的规律，特别是如何才能将人才的引进及培养与社会的需求正确结合？关联规则挖掘是数据挖掘的一个重要的研究分支，其主要的研究目的是从大型数据集中发现隐藏的、有价值的属性间存在的规律。本文用关联规则挖掘技术在这方面做了一定的探索和研究，期望能得到一些有益的启示。

1 相关概念

1.1 关联规则

定义：设I= {i1,i2, . ..,in}是项的集合。包含K个项的项集称作K项集。设D是数据库记录的集合，其中每个事务T是项的集合，且T⊆I。设X是一个项集，事务T包含X当且仅当X⊆T。

关联规则是形如X⇒Y 的蕴涵式，这里X⊂I,Y⊂I，且X∩Y=Φ。X称为规则的左部或规则的前提(LHS)，Y称为规则的右部或结论(RHS)。

度量规则的参数是支持度与置信度。支持度是指数据集中的实例同时包含条件属性与决策属性的共同概率，支持度揭示了规则的重要性。置信度表示实例在包含条件属性的前提下，也包含决策属性的条件概率，它揭示了规则的可信度。在粗糙集理论中支持度与置信度可以表示为：support(x⇒y) =p(x∪y)

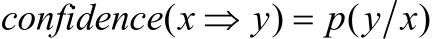
其中P(X)表示X在数据D中出现的概率，其余相似。support(x⇒y)指X、Y在D中同时出现的概率；confidence(x⇒y)表示在X出现的前提下Y出现的条件概率。若得到的规则同时满足支持度不小于支持度阈值和置信度不小于置信度阈值，则该规则有意义。

1.2 决策表的属性约简

在决策表中，不同的属性可能具有不同的重要性。要找出某些属性的重要性，就要从表中去掉一些属性，再来考察没有该属性后分类会有怎样的变化，若去掉该属性后分类变化较大，则说明该属性强度较大，重要性高，反之，则说明该属性重要性低。决策表的一般属性约简的具体步骤：

(1) 求多个条件属性C1,C2,C3,…,Cn的等价类；

(2) 计算从C中分别去掉C1,C2,C3和Cn后所有属性集下的等价类；

(3) 求决策属性D与条件属性C的依赖度；

(4) 检查从C中去掉C1,C2,C3或Cn时分类的变化情况，若分类发生较大变化，说明该属性不可去，否则可去。

2 关联规则挖掘模型

在大量实践的基础上，总结出了一个相对成熟的基于粗糙集的关联规则挖掘模型，其基本思想和步骤如下。本文应用基于粗糙集的关联规则的挖掘过程分为三步：数据预处理，属性约简与关联规则的挖掘，见图1。

(1) 数据预处理：通过对高校人事数据的初始信息进行数据清洗，缺失值处理，转换及数据选择，获取初始信息表，且初始表转换为决策表形式，并明确条件属性集和决策属性；

(2) 属性约简：对条件属性进行约简，删除多余属性，在此基础上利用文献[1]中的算法进行属性约简并生成约简属性集；

(3) 关联规则挖掘：输入支持度阈值和置信度阈值，根据数据约简结果，利用粗糙集理论文献中的算法，进行关联规则的挖掘。

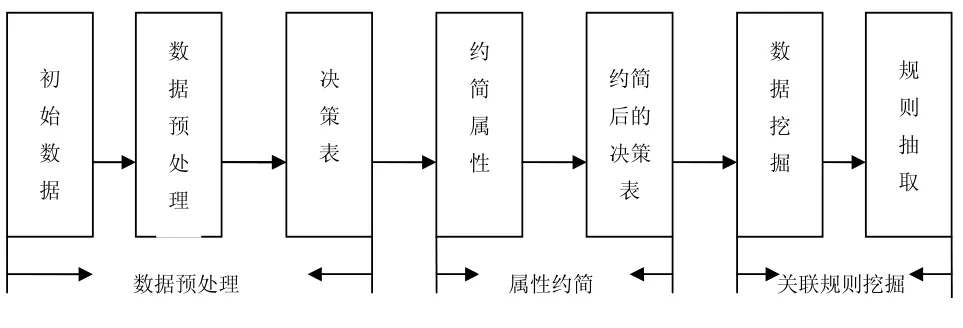
图1 基于粗糙集的关联规则模型

3 关联规则挖掘技术在教师成长中的应用

下面以高校教师成长信息为例(本文以职称为教授和讲师作为高校人才成长的标志，根据参加工作时间的长短和目前职称来判断教师成长的快慢)，说明基于粗糙集的关联规则挖掘算法的实施过程。

根据上述构建的数据挖掘模型，利用属性约简算法对高校教师数据进行约简。首先进行数据预处理，其次求出约简，并在此基础上根据值约简等减少属性和个体数目，最后提取规则应用于新对象的分析和预测。

3.1 数据预处理

本文以本人所在高校教师数据为例，采用关系数据库模型，经关系数据库的导入及连接并进行抽象、离散化等预处理。将影响教师成长的因素：性别、政治面貌、学历、毕业学校、年龄、学历变动、现聘职称、教龄、教学能力和科研能力作为系统的条件属性C，而将教师的成长速度作为决策属性D。

对于具体的数据处理时可先将其抽象、离散化、使后续的表格简洁明了。性别(1：男2：女)，年龄(1：25—30 2：30—35 3：36—40 4：40—45 5：45以上)，教龄(1：1—5 2：10—15 3：16—20 4：21—25 5：25 以上)，政治面貌(1：党员 2：其他)，毕业院校(1：重点高校 2：普通高校)，学历(1：学士 2：硕士)，现聘职称(1:教授 2：副教授3：讲师 4：助教)，评定年龄(1: 25—30岁, 2: 31—35岁, 3:35—40岁, 4: 40岁以上)，学历是否变动(1：是 2：否)，教学能力，科研能力(1：高 2：中 3：一般)和成长(1：快 2：中 3：慢)。

以上划分等级的标准是根据以往实际经验和具体的数据而确定，按以上的规则概化和离散化原始数据，根据以往的经验和实际的情况可判断性别，年龄，政治面貌，学历变动为冗余属性。删除其中的冗余属性得到预处理后的数据表如表1所示。

表1 预处理后的教师数据

3.2 属性约简

表1中的数据只是对初级数据的简单分类和离散化，首先删除表1中的冗余对象，然后对其进行属性约简，通过计算可得 U 的属性约简集为{C4,C5,C6,C7} 。此时对属性约简后对应的表再次删除冗余对象，得到最终属性约简后的数据如表2所示。为了计算方便将条件属性在表中以C1，C2，…，C7来表示，其中C1 = 教龄，C2=毕业院校，C3=学历，C4=现聘职称，C5=评定年龄，C6=教学能力，C7=科研能力，D=成长。

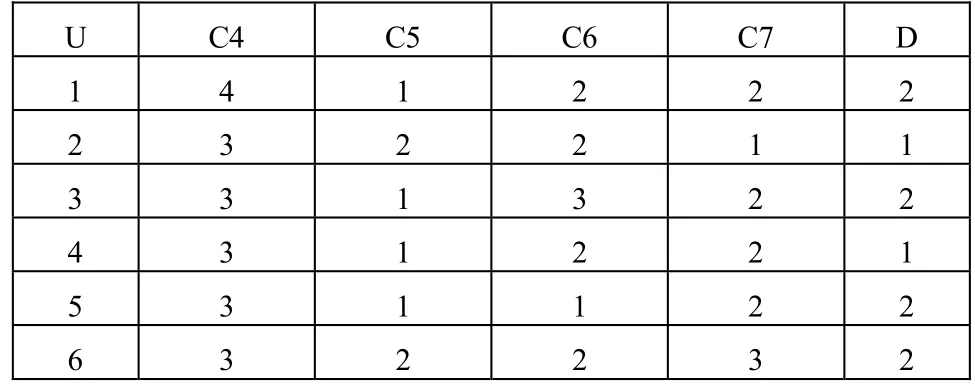
表2 约简后的数据表

续表

3.3 关联规则挖掘

根据上面得到的约简，通过属性之间的隐含关系来挖掘关联规则，给定支持度阈值 5%，置信度阈值 80%，可得到同时满足支持度阈值和置信度阈值的项目集生成的关联规则有：

Rule 1(现聘职称=4)&(评定年龄=1)&(教学能力=2)&(科研能力=2)=＞(成长速度=2)；

Rule 2(现聘职称=3)&(评定年龄=1)=＞(成长速度=2)；

Rule 3(现聘职称=3)&(评定年龄=3)=＞(成长速度=3)；

Rule 4(现聘职称=2)&(评定年龄=1)=＞(成长速度=1)；

Rule 5(现聘职称=2)&(教学能力=1)&(科研能力=1)=＞(成长速度=1)；

Rule 6(现聘职称=1)&(评定年龄=4)=＞(成长速度=1)。

以上规则的含义如下：由第一条规则可知现聘职称为助教，评定年龄在25到30，教学和科研能力中等，则可以断定教师的成长速度中等；由第二条规则可知：现聘职称为讲师，评定年龄在25到30，可以断定该教师的成长速度中等；第三条规则说明如果现聘职称是讲师，评定年龄在35到40，断定教师的成长速度慢；第四条规则说明职称是副教授，评定年龄在25到30，可以断定该教师的成长速度快；第五条规则说明职称是副教授，教学和科研能力高的教师成长速度快；第六条规则说明职称是教授，评定年龄是 40以上的教师成长速度快。

由以上规则可以得出：现聘职称，评定年龄，教学能力和科研能力对教师成长的快慢有显著影响。现聘职称是助教，教学和科研能力都中等的教师，属于成长速度中等的类型；而在 30岁前评为副教授的教师，成长速度快；职称是副教授，教学和科研能力较强的教师的成长速度也是快速型的。因此，如果高校希望教师能够快速成长，则在人才引进时就要多考虑教师的教学和科研能力，在人才的考核方面提出新的机制来改变传统的只看学历和毕业院校等情况。