基于多项式回归算法的锂电池SOC估测
2011-06-11曾洁卜凡涛
曾洁,卜凡涛
(大连交通大学电气信息学院,辽宁大连116023)
0 引言
锂离子电池以其特有的性能成为21世纪发展最理想的新能源之一.由于锂离子电池单节工作电压高(可达3.6 V,是镉-镍电池的3倍)、体积小(比同容量的氢-镍电池小30%)、质量轻(比同容量的氢-镍电池轻50%)、单位重量的能量高(可达140 Wh·kg-1,是镉 -镍电池的2~3倍,氢-镍电池的1~2倍)、无记忆效应、无污染、自然放电量小、循环寿命长,已在便携式电器如笔记本电脑、数码设备、移动通讯设备以及新能源汽车中得到普遍应用[1].
锂离子电池虽然已得到广泛的应用,但是对于锂离子电池的荷电状态(SOC)的估测仍然困扰着人们.现如今的部分便携式电器和电动汽车所使用的锂电池虽然也配备有电池管理系统,有剩余容量的显示,但是却都处于估测阶段,都不能更加准确地反映给用户,因此严重影响了它的使用,尤其在新能源汽车的推广应用上.为此,本文提出了一种非常实用的能够更加准确、实时计算剩余容量的方法,采用开路电压法与安时计量法的结合,用回归分析法来寻找电池静态开路电压与其静态初始SOC的变化曲线;而电池动态SOC估测则采用成熟的安时计量法.
1 SOC估测方法
1.1 SOC 的定义
荷电状态(SOC)是描述电池剩余容量的物理量,是电池使用中对用户较为重要的参数之一.SOC(State of Charger)不能直接从电池本身测得,需要通过电池的特性参数(比如:电压、电流、内阻等)估测所得.SOC是研究电池性能变化的重要参数之一,对于电池的管理有重要的意义[2].
SOC与剩余容量的关系可表示为:SOC(%)=(CN-C0)/CN,其中,C0为负载上测量到已用去的容量(A·h),CN为电池出厂的额定容量(A·h),(CN-C0)为电池剩余容量(A·h).
1.2 几种SOC估测方法比较
传统的估测电池SOC的方法有很多,他们都适应于不同的场合.目前主要的几种常用的电池SOC估测方法如下:
(1)开路电压法:电池的开路电压在数值上接近电池电动势,对于某些电池(如镍氢电池),用开路电压法可以很好的估计SOC.虽然锂电池的线性度稍微差点,但是当电池静置一定时间后仍可以作为估测SOC的重要参考.所以开路电压法适合于电池静置长时间的场合下,当电压达到稳定后才可作为SOC的参考.它不能用在电池实时在线的动态SOC估测[3].
(2)卡尔曼滤波法:卡尔曼滤波法从本质上来说是一种最优化估计法,对电池的各个状态参数做出最小方差意义上的最优化估计.卡尔曼滤波法在不考虑实现复杂度的情况下是一种比较好的方法,它能够实时在线检测电池的SOC,同时还能估测出误差,精确度也较高.但是卡尔曼滤波法对于处理器的要求较高,电路较复杂,投入较大[4],对于高压大功率动力电池的SOC估测很有意义,但对一些低压小功率的电池的SOC估测不便使用.
(3)内阻法:电池有直流内阻与交流内阻之分,他们与电池SOC都有一定的关系,但却不存在明确的线性关系.电池内阻是在不断变化的,当电池剩余容量较大时电池内阻较小,而剩余容量变小时却变的较大,对于这点可以应用在检测诊断电池的好坏方面.
(4)安时(Ah)计量法:Ah计量法是最常用的SOC估测方法.如果充放电起始状态为SOC0,那么当前状态的SOC为:其中,CN为额定容量;I为电池充放电电流,电池放电时取正,充电时取负;η为平均充放电效率,由于电池存在内阻,电池充放电时就有能量损失,它受电池充放电电流、温度、SOC等影响.
安时计量法可以应用于所有的场合下,但是却存在两个问题:由于测量精度问题可能引起误差;起始状态SOC0无法测得.所以,安时计量法一般要与另一种方法结合来解决自身的问题,本文为此提出了一种基于多项式回归算法的开路电压法与安时计量法相结合的电池SOC估测方法.
2 多项式回归法的SOC估测方程的推导
2.1 电池SOC估测的基本思路
虽说安时计量法是电池SOC估测的核心方法,但是安时计量法却无法测得电池在充放电前的静态初始SOC0,于是需要用开路电压法来寻求电池的初始SOC0.第一步需要通过大量实验来寻找电池静态开路电压与其SOC的对应关系,在此基础上利用回归分析法拟合出开路电压与SOC的关系曲线方程,这样就可以在电池启动前通过把测得电池的开路电压带入方程算出其初始SOC0;第二步就可以用安时计量法来测量电池实际消耗和补充的容量,进而通过SOC=SOC0-得到电池的当前SOC量.
2.2 多项式回归分析[5]
设变量x、Y的回归模型为:

式中,p是已知的;β0,β1,…,βp是未知参数;ε 服从正态分布N(0,σ2).记EY=y,因而可得式(2):

上面的回归模型称之为多项式回归.多项式回归是一元非线性回归的一种特殊情况.它可以通过变量代换线性化.如果令x1=x,x2=x2,…,xp=xp,那么多项式回归模型就可以变成多元线性回归模型 Y=β0+β1*x1+β2*x2+… +βp*xp+ε,所以对多项式回归的参数估计可利用多元线性回归的参数估计算法.
对变量x,Y进行n次试验观察,得到n对观察值(xi,yi),i=1,2,…,n.则可以得到正规方程组如下:

将观察值带入上述方程组(3)中,通过解此正规方程组便可以得到估计值 β0,β1,…,βp.
2.3 电池SOC估测拟合曲线方程的实验推导
实验条件是1台电池多功能参数测量仪(可以测得电池电压、充放电电流、温度、安时量、内阻)、1组锂离子电池(由3节3.6 V的单体电池串接而成,其额定电压约为11 V,额定容量为2.2 Ah.)、2个20 W 的 4 Ω 电阻负载、1个定时器以及连接导线.实验前先将锂电池组进行充电至其额定容量CN,其实际初始开路电压约为12.7 V;然后通过电池多参数测量仪的电流测量通道串接2个20 W的4 Ω电阻负载进行放电,放电过程中仪器可以测量负载消耗的安时量C0,由于电池存在内阻,所以一开始其放电电流约为1.4 A,放电持续5 min后停止,电池测量仪器测得的累计放电安时量约为0.11 Ah,由 SOC(%)=(CNC0)/CN可计算出其SOC为95%,等待30 min后电池基本达到静态后则由电池多功能参数测量仪测得其对应开路开路电压OCV为12.43 V.整个实验依次类推,在实验过程中,前5个采样点均是电池放电5 min后,断开电路停止放电,在等待30 min后再测量其对应的开路电压值;以后的8个采样点放电持续时间改为10 min,然后断开电路停止放电,等待30 min后再测量开路电压值.根据SOC(%)=(CN-C0)/CN可以计算出电池的SOC,整个实验按照上述操作步骤进行最后得到表1所示的电池开路电压OCV与其对应的SOC实验数据.如果把这13个采集点描述在坐标轴上可以得到图1所示结果,由图1可以看出电池开路电压与对应的SOC并非线性关系.

表1 电池开路电压OCV与其对应的SOC实验数据

图1 实验数据在坐标轴的描述
根据各离散点的分布形状,并考虑到运算量问题,假设回归模型的最高次幂为三次,于是我们可以令回归方程:
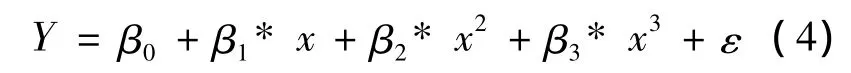
由多元线性回归特性可得:

根据表1中的实验数据可以算出:

将上述计算出的各系数分别带入(5)式中,于是可得到如下方程组:

解上述方程组可得:β1=-112.811;β2=38.927 27;β3= - 1.811 57;

上述方程(7)便是由实验推导出的反映电池静态初始SOC与其开路电压间的回归方程,如果把(7)式描述在坐标轴上可得图2所示的曲线图.

图2 回归方程在坐标轴的描述
如果把实验得到的数据与按回归方程(7)式计算的理论数据描绘在一个坐标轴上来对比他们之间的关系,可得图3所示效果.理论计算值与实验值最大误差为4.293 61%,最小误差为0.356 96%,如果根据国家“十五”“863”电动汽车重大专项对电池及其管理系统的要求[6],电池荷电量预估误差<8%.这完全符合预估误差<8%的要求,所以,可以把(7)式作为电池开路电压反映其SOC的曲线方程.

图3 回归方程计算结果与实验数据的比较
3 实验验证
为进一步证明实验推导出的电池静态开路电压与其SOC的回归方程的准确性,又选择一组同类型的新锂电池作前面类似的实验,分别记录下13个采样点的开路电压值及其SOC的实验值,之后将13个采样点的开路电压分别带入前面推导所得到的回归方程(7)式中,分别可得13个采样点所对应的理论SOC值(如表2所示).通过比较13个采样点所对应的实验SOC值与理论SOC值,不难看出SOC的实验值与理论值都非常接近,其最大误差为5.790 89,最小误差为0.705 33.实验结果说明基于多项式回归法拟合出的电池开路电压与其SOC的曲线方程能够较为准确地反映电池开路电压与其SOC间的关系,该方法简单实用,对电池管理研究与实践有一定的参考价值.

表2 SOC的实验结果与理论值的比较
4 结论
通过实验和多项式回归法推导,得到电池的静态开路电压与其静态初始SOC关系曲线,用安时计量法来计算电池的动态SOC,利用公式SOC来计算得到.此方法已在电池管理系统中得到应用,实际测量效果良好,完全可以满足电池管理系统对电池剩余容量估测的需求.另外经过大量的实验还存在以下两点需要注意的问题:
(1)开路电压与SOC的关系曲线并不是一成不变的,如果在环境恶劣的环境下可能会出现较大的波动,使数据失真,因此要针对电池不同的用途来寻找关系曲线,这样估测出的电池SOC精确度会更高些;
(2)充放电倍率η需要通过大量实验来寻找,η也是随电池用途变化的,在本实验中由于只串联8 Ω电阻负载,另外使用的电池内阻也较小,热能消耗较少,所以把η作为1来处理.但在实际的用途中不可避免会有电能损失,所以需要经过再做大量的循环实验来估测η的大小,这样估测结果会更加准确.
[1]果炳焜,徐徽,王先友,等.锂离子电池[M].长沙:中南大学出版社,2002:1-33.
[2]林成涛,王军平,陈全世.电动汽车SOC估计方法原理与应用[J].电池,2004,34(5):376-378.
[3]蔡正英,桂长.电动自行车电池开路电压与放电容量的关系[J].电池工业,2007,12(6):366-369.
[4]林成涛,王军平,陈全世,等.用改进的安时计量法估计电动汽车动力电池SOC[J].清华大学学报,2006,46(2):247-251.
[5]汪蓉鑫.数理统计[M].西安:西安交通大学出版社,1986.
[6]陈全世,仇斌,谢起成,等.燃料电池电动汽车[M].北京:清华大学出版社,2005.
