城市交通紧急疏散路径优化

郑长江，卢为杰

(河海大学 土木与交通学院，江苏 南京 210098)

0 引言

面对城市突发性灾难事件，及时快速的交通疏散是防止和减少人员伤亡最根本的方法［1］.应急交通疏散的深入研究已被列为我国“十一五”科技攻关计划重点实施项目之一，由于当前国内应急机制和体系的建立尚处于探索阶段，应急疏散时主要依靠行政命令，采取良好的路径选择策略有助于提高疏散决策的科学性.因此，为提高疏散效率，缓解因紧急疏散时大量车流拥挤到疏散路网上，造成车速急剧下降、道路阻塞严重等情况，迫切需要对应急疏散路径方案进行优化分析，进而确定适合我国国情和符合城市交通运输环境的疏散路径研究方向，建立相应的方法体系.

刘小明［2］等在“应急交通疏散研究现状与展望”中指出国内外应急疏散理论与技术研究关键之一是解决疏散路径选择问题，即如何在有效的时间内，将事故发生地点集结的待疏散车辆尽快疏散到安全区域.高明霞，贺国光［3］等研究采用合理规定源点车辆的分批次出发时间和路线安排的方法保证区域性疏散大批车辆集体性出行时安全、有序.安实、崔建勋［4］等基于CTM元胞传输模型理论，采用最优化与仿真结合的区域疏散交通管理模式，以疏散车辆数最大化和疏散出行总时间最短为目标对疏散交通规划进行优化.陈岳明，萧德云［5］在描述路网疏散问题的基础上，研究疏散路线的构建和各疏散路口的路网分配问题，构建以总疏散时间最小化为目标的疏散模型.Thomas J.Cova［6］探讨了基于道路的最短行程疏散路径，Yamada［7］运用最小成本流问题进行疏散交通分配，提出了最短路撤退规划(SEP)方法，即全部疏散者撤离至所选避难所的行程总和的最小化.所构建的疏散目标函数只考虑行程时间和绕行距离中的某一方面，这种单一目标的设定在复杂路网应用当中容易引起严重的交织和拥堵［8］.图1为典型区域性疏散路网示意图.

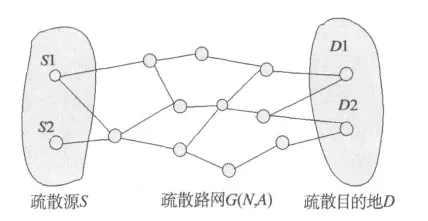
图1 典型区域疏散路网

1 研究目标

在实际疏散过程中，我们需要在时间t内安全地将影响区Si的交通量Pi通过路网G(N，A)引导并转移到目的地Dj，对于每个Pi应当分配到对应一条疏散路径上.要实现安全转移目标就要使得出行者总的行程距离DT与疏散路网清空时间TC道路拥堵最小化.文章构建关于交通出行者总行程DT与疏散路网清空时间TC的线形组合最优目标函数Z，求解并找寻最优疏散路径向量集X，实现疏散路径的优化.决策者根据突发事件的属性和交通小区受到威胁的严重程度决定权值w的大小，构造从事疏散源与目的地之间的快速疏散路径模型，用于控制疏散区域的疏散车辆安全迅速地疏散到安全区域.

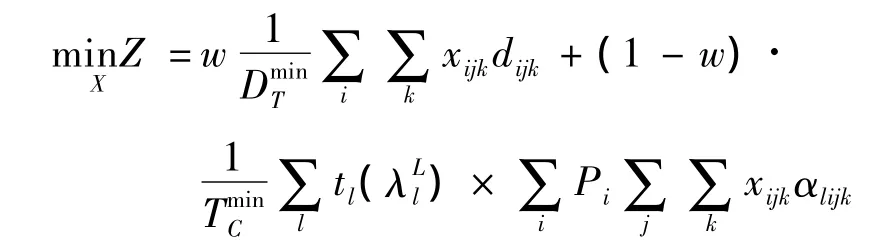
约束条件:

目标函数Z是出行者总的行程距离DT与疏散路网清空时间TC的线形组合函数，问题的关键是产生最优疏散路径向量X.其中:

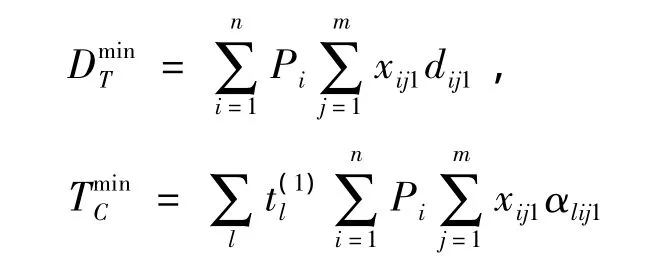
符号说明:i为疏散源 Si编号，i=1，2，3…;j为疏散目的地 Dj编号，j=1，2，3…;k为第k条最短路编号;l为疏散道路连接线集A编号;xijk为若分配到第k条连接i与j最短路径为1，否则为0;w为权重，由决策者定;为当所有出行者分配至第1最短路的出行总行程;为所有出行者按照用户最优疏散路径以最大车速行驶路网清空时间(无阻塞情况);dijk为路径xijk的总长度;Pi为疏散源Si的出行车辆总数;λi为疏散源Si的车辆到达率;为进入路段l的到达率总和;为路段l的最大允许到达率，其中∈是路段阻塞概率峰值;为路段l的最小可能通过时间;为给定到达率情况下通过路段的可能通过时间;αlijk为若疏散路径xijk包含路段l为1，否则为0;Cj为疏散目的地Dj的容量.

2 算法设计

步骤1 路网描述步骤:给出区域疏散路网G(NT，AT)，其中 NT为节点数，AT为边线条数，使用 k 最短路算法［9］确定 1st，2nd，3rd，…，kth 最短路集，对应于输入节点i.

步骤2 分析步骤:

步骤3 计算所有道路连接a1其中a1∈A的上游车辆到达率，保证低于道路阻塞密度.

步骤4 计算a1∈A的相应道路最大出行时间值对于路段最大疏散交通流密度，并由给出所有路弧a1的线形通过时间函数

步骤5 综合步骤:

步骤6 根据公式构造并求解系统最优路径模式，产生路径分配向量X.

步骤7 用M/G/c/c模拟软件进行仿真实验，在获得路网总清空时间TC、所有车辆总行程时间DT和道路拥堵程度的基础上评价路网G(NT，AT)疏散路径规划效果.

3 实验分析

本节将通过实例对上述优化方法进行验证，实验任务是设计最优疏散方案，并从路网清空时间、出行距离、阻塞概率等方面的表现检验疏散方案的有效性.因此假定需要从S1，S2，S3疏散4500辆车到达疏散目的地D1，各疏散源点的车辆到达服从泊松分布，λ1=λ2=λ3=1200辆/h，路网几何结构和道路连线长度如图2、表1所示，设定车道数W1=1车道，最大车流密度Kmax=200辆/km/车道，自由流车速=55 km/h，采用M/G/c/c软件得到表2所示的各路段在不同车辆到达率下的行程时间特征值.

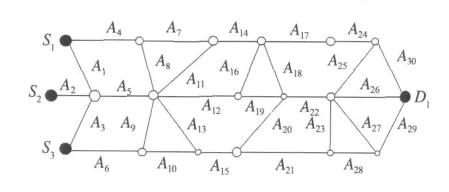
图2 疏散路网

表1 路网几何特征

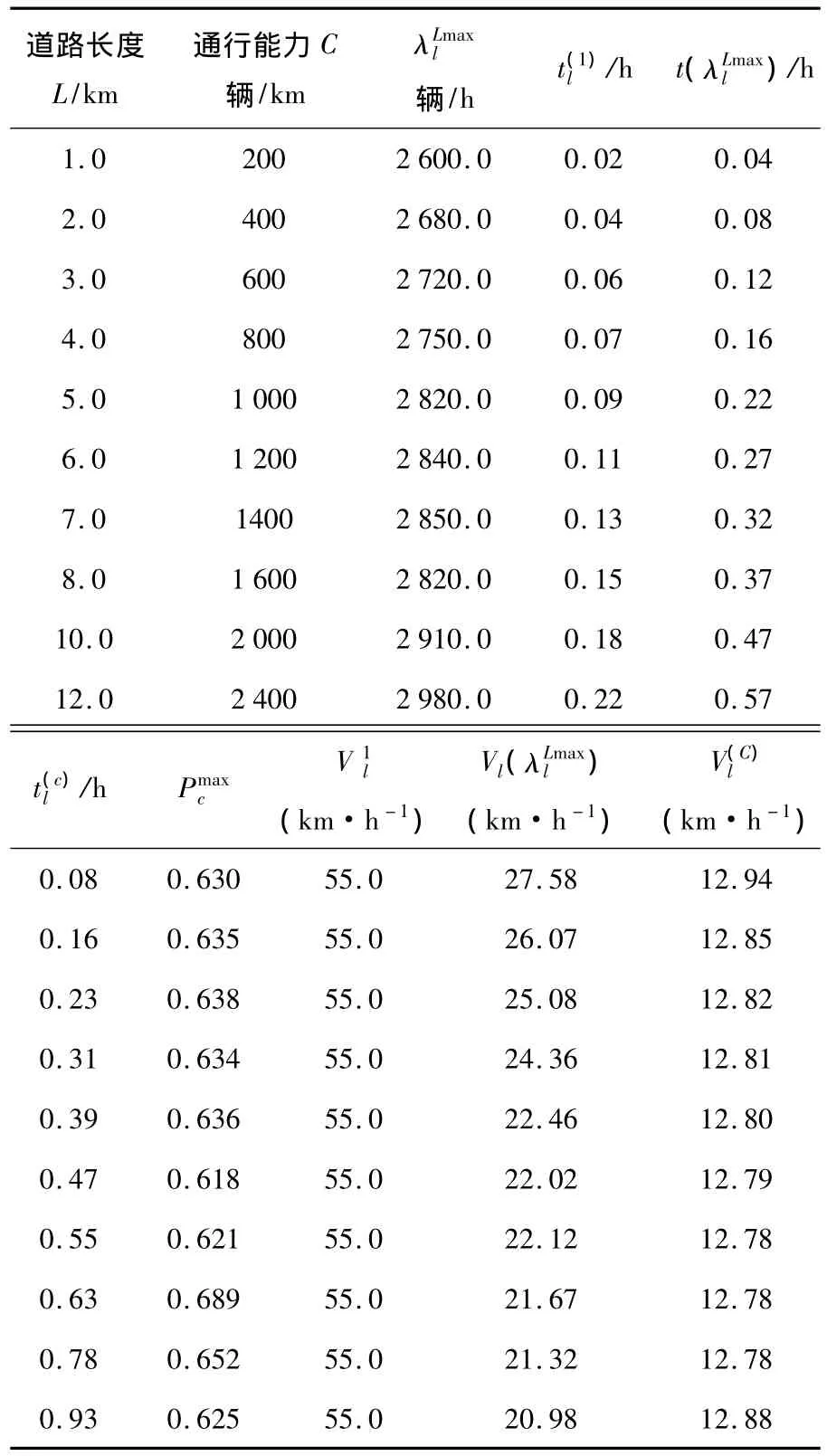
表2 路段行程时间特征

3.1 用户最优路径策略仿真分析

用户最优策略是一个较为直观的疏散方案，出行者认为选择最短路径可以最快捷地驶离危险区域，因而所有疏散车辆都被分配到一条最短疏散路径上，如图 3 所示，最短路径 EP1={RS1，1，RS2，1，RS3，1}=36，对应各疏散源点的疏散路径为:

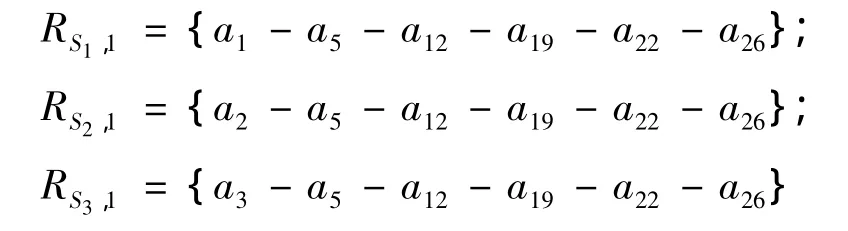
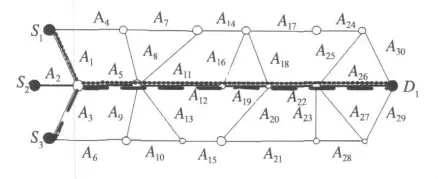
图3 用户最优路径分配

采用M/G/c/c模拟软件进行仿真实验，从表3实验结果显示，在路段a5及a19呈现了显著阻塞.例如从a1，a2，a3出发行驶至a5的路段形成了超出38%的阻塞概率，造成车辆阻滞，须排队等待通过;在a19路段中，通行能力仅为600辆/h，而来车率却为2 720辆/h;a12的通行能力为1 600，高峰时有2 870辆/h的来车率，显然此策略不能确保快速疏散.

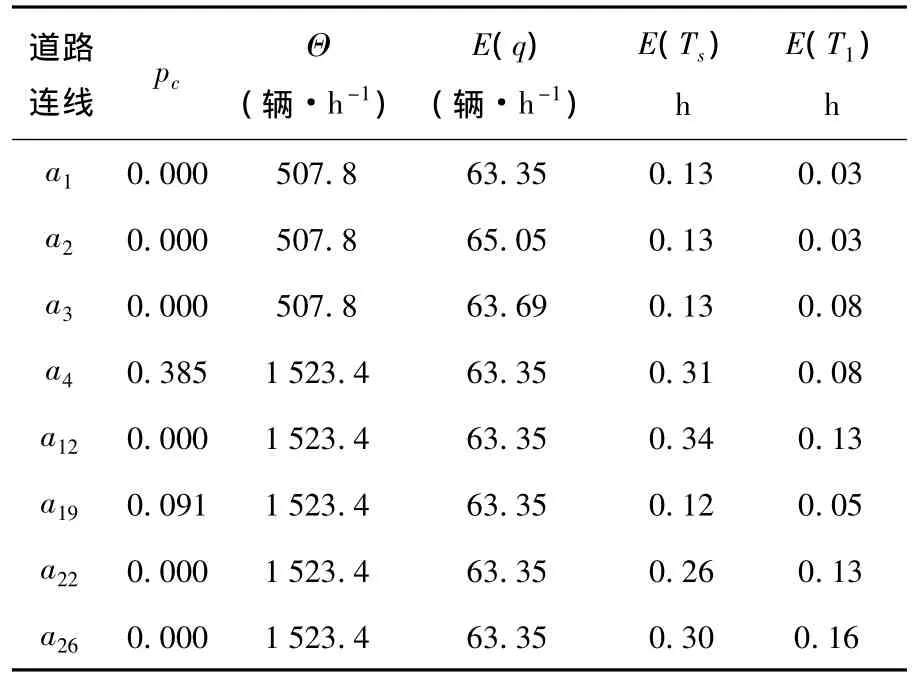
表3 用户最优疏散路径规划实验结果

3.2 系统最优疏散策略

考虑延误的总成本最小，通过最优目标函数Z的求解得到疏散路径最优决策向量为X={x1，1，1=1，x2，1，10=1，x3，1，11=1}，即 s1的交通量沿着第1条最短路径疏散，s2沿第10条最短路径，第11条最短路承担s3的疏散车流，如图4所示.其中 :

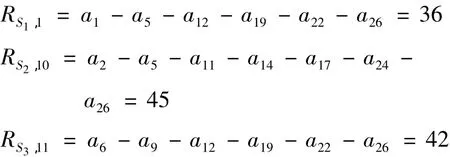
图4 系统最优路径分配表

同样采用M/G/c/c仿真软件模拟，表4显示尽管 a5，a12，a19，a22的期望出行时间 E(Ts)是自由流通过时间E(T1)的两倍多，但是与阻塞概率相比还是适宜的.再者，系统最优策略疏散总时间为 TSPC=2.30 h，行驶距离总计 DSPT=183，260 km，由于道路利用更均衡并未形成道路阻塞，系统优化策略可以确保疏散过程的安全.

表4 系统最优疏散路径规划实验结果

3.3 实验结果分析

尽管采用系统最优疏散路径策略时会相对增加出行总距离，但它使得路网阻塞概率、拥堵水平和路网清空时间等显著下降，灾害对疏散者危害所体现的时间成本得到控制.表5显示，采用系统最优路径策略可使疏散时间减少22%，最大阻塞概率下降38%.

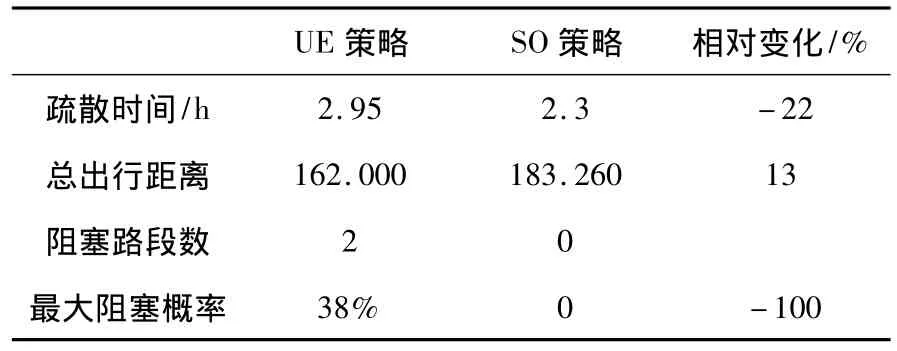
表5 实验结果对比分析

4 结论

本文重点研究疏散路径优化问题，将k最短路算法融合到系统最优疏散路径的求解当中，有助于更好利用道路网络资源.从实验分析得到，M/G/c/c独立分布排队模型可以较好地模拟分析疏散规划时路网延误、阻塞问题.展望未来，仍需进一步考虑不同出行方式和不同的疏散流量加载方式对疏散效果的影响，当出现不确定因素如路网设施存在瓶颈制约时，算法有效性也需要提高和改进，以期能适应更大规模路网的应用需求.

［1］ALEXANDER D.Principles of Emergency Planning and Management［M］.London:Oxford University Press，2002.

［2］刘小明，胡红.应急交通疏散研究现状与展望［J］.交通运输工程学报，2008，8(3):109-115.

［3］高明霞，贺国光.动态系统最优的疏散路线与出发时间综合优化模型［J］.系统工程，2009，27(6):73-77.

［4］安实，崔建勋.基于最优化与仿真的区域疏散交通管理研究［J］.交通运输系统工程与信息，2009，9(5):103-109.

［5］陈岳明，萧德云.应急疏散过程建模及其算法研究［J］.交通运输系统工程与信息，2008，8(6):96-100.

［6］COVA T J，JOHNSON J P.Microsimulation of neighborhood evacuations in the urban-wild land interface［J］.Environment and Planning，2002，34:2211-2229.

［7］YAMADA T.A network of approach to a city emergency evacuation planning［J］.International Journal of Systems Sci-ence，1996，27(10):931-936.

［8］HELBING D，SCHHOF M，Stark H U，et al.How individuals learn to take turns:Emergence of alternating cooperation in a congestion game and the prisoners dilemma［J］.Advances in Complex Systems，2005，8(1):87-116.

［9］ANANY LEVITIN.算法设计与分析基础［M］.北京:清华大学出版社，2004.