残留应力对倾斜裂纹的变形和曲折特性的影响

马有理，朱 琳

(1.哈尔滨商业大学 能源与建筑工程学院，哈尔滨 150028;2.哈尔滨商业大学轻工学院，哈尔滨 150028)

对于管道等机械构件，在制造过程中由于结构的需要往往要在部件中开槽或开孔，而且还可能存在其他的制造缺陷.在使用过程中在应力的作用下由以上的缺陷而产生裂纹几乎是不可避免的.作用于机械构件上的载荷未必就一定是与裂纹相垂直(裂纹的开口方向)，而是与裂纹形成一定的角度，包含了裂纹的开口方向(Ⅰ型)和裂纹的滑移方向(Ⅱ型)的混合型条件下的情况比较多［1－2］.到目前为止，对于单纯的Ⅰ型裂纹，使用有效应力扩大系数Keff对裂纹的变形的特性的评价已经有很多的相关报道［3－5］.但是在混合型条件下，由于裂纹在变形过程中裂纹的上下表面要产生滑移，此时如果裂纹的表面呈锯齿状，则在裂纹开口较小时裂纹上下表面由于相互接触而使裂纹的变形受到影响.另一方面，对于实际的构造物中存在的裂纹，要想直接测得其周围的应力的大小有时是很困难的.对此提出了一种不是通过应力，而是通过测量裂纹的不连续位移量V(开口方向:Ⅰ型)、U(滑移方向:Ⅱ型)，而直接计算裂纹端部的应力扩大系数(KⅠ)mes和(KⅡ)mes，从而评价裂纹的变形特性的方法.

以上的裂纹在混合型应力的作用下，如何预测裂纹的扩展方向，是断裂力学研究的一个主要方面.目前虽然也有一些有关的研究报道，但都是以机械加工的槽孔作为预裂纹，即曲折疲劳裂纹的传播是在完全没有受到预裂纹上下表面相互接触的影响［6－8］的情况下进行的.在此，利用表面呈锯齿状的倾斜预裂纹，曲折裂纹的扩展长度到大约1 mm左右为止，从曲折裂纹开始传播后大约每隔0.1 mm对裂纹进行一次观察.最后对预裂纹周围的压缩残留应力和裂纹上下表面的相互接触对疲劳曲折裂纹扩展的影响进行了探讨.

1 实验方法

1.1 试验片的制作

实验用钢材为S45C(相当于中国的45#钢)，化学成分及机械性能分别如表1，2所示.图1是β=45°带夹具实验片的形状和尺寸.首先，用平面研磨将试料磨成所希望的厚度t=2 mm，按图1中粗线的尺寸加工.为了使产生的裂纹能够在实验片的中央向两侧方向进展，实验片的中央开有φ=1 mm的中心孔.实验片与夹持实验片的夹具A于图中的左右两端E点处用电弧焊相连接.为了消除机械加工的影响，用真空炉做600℃、1 h保温的回火热处理，然后用螺栓将夹具B固定其上即可.疲劳实验是在循环速度20 Hz，最大应力值бmax=140 MPa的正弦波载荷下进行的.实验开始直到发现裂纹发生为止应力比(最小应力与最大应力之比)

表1 材料的化学成分质量百分比

表2 材料的机械性能

图1 用来制作倾斜裂纹的带夹具的试件

R=－1，此后R=0的条件下直到从中心算起的单向裂纹长度a≒3 mm疲劳实验结束.然后，将图1中的阴影部分加工出来，作为具有倾斜角为β=45°裂纹的实验片，如图2所示.

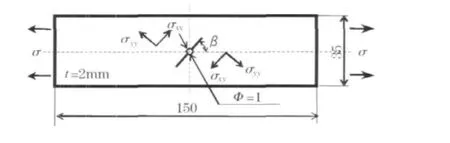
图2 倾斜裂纹试件的尺寸

在以下的讨论中，由图1加工出的实验片(图2)直接使用，即为疲劳预裂纹实验片;但如果对加工出的图2实验片进行回火热处理后再使用，则为回火预裂纹实验片.

1.2 不连续位移的测定

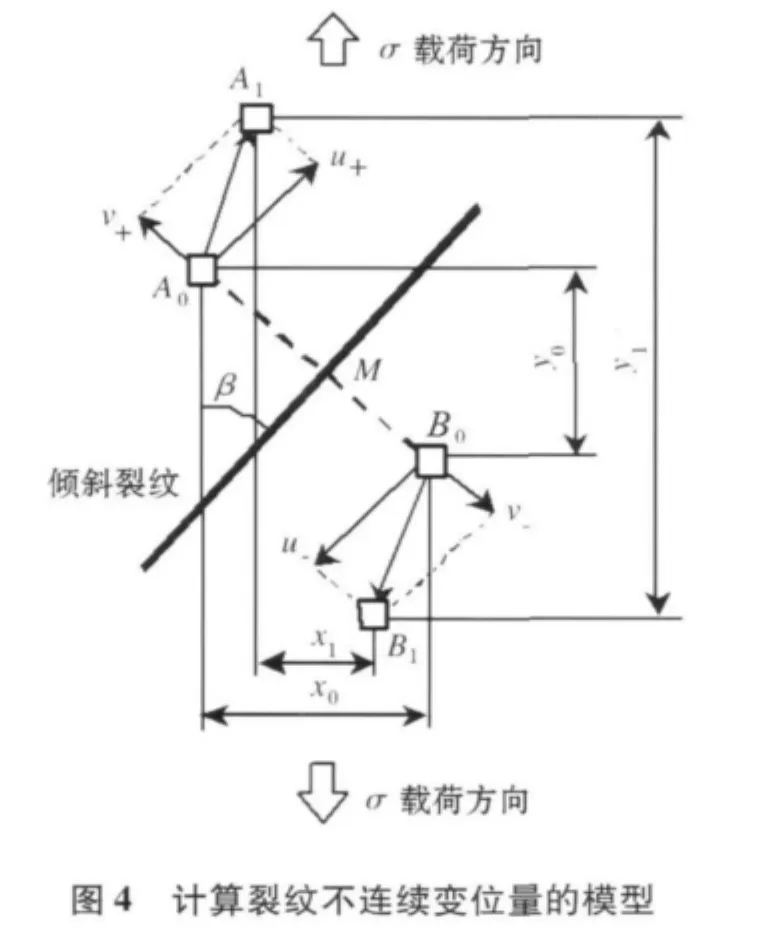
图3是沿着裂纹两侧打印的微型压痕标记的示意图.图3中的每一对压痕都是与裂纹相垂直的.裂纹在受载时测量每对压痕与裂纹垂直方向及平行方向的距离，它们与卸载时相应距离的差为裂纹开口方向位移量V及滑移方向的变位量U.图4是利用几何关系计算裂纹开口及滑移方向位移量的模型.比如裂纹两侧的一对压痕在没有载荷作用时其位置为A0和B0，但在受到试验片长轴方向的载荷б作用时其位置分别变为A1和B1.如果线段A0、B0的x方向及y方向的分量分别表示为x0和y0，而线段A1、B1的x方向及y方向的分量分别表示为x1和y1，则根据图中的几何关系可以容易的求出裂纹在该点的V及U的近似值，如公式1所示.

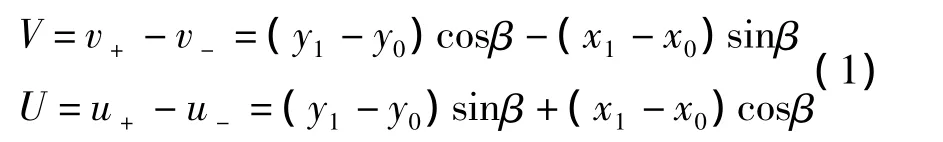
1.3 压缩残留应力分布的测定

根据X－射线应力测定法，利用照射面积为1 mm×1 mm的X－射线对沿着预裂纹的压缩残留应力进行了测量［9］.X－射线的条件包括:Cr－Kα的衍射线;射线的摇动范围为(±2.5)°;利用射线近似的方法确定反射线的最大值，X－射线的应力值是由2α—sin2ψ曲线的斜率再进行最小二次幂的近似法而确定的，在这里材料的应力常数为－318.2 MPa/°.

1.4 曲折角度的测量

图5是预裂纹在载荷σ的作用下，裂纹发生曲折并继续传播的模型图.预裂纹上任意一点为A，预裂纹的端部的点为B，曲折裂纹的端点为C，则在曲折裂纹的传播过程中通过测量ΔABC中各条线段的长度，可以很容易地算出图中所示的角度θmes，此角即作为曲折裂纹的曲折角.曲折裂纹长度大约每0.1 mm为间隔，对曲折裂纹的曲折角度进行了观察测量.

图5 曲折裂纹的曲折角度的测量

2 实验结果

2.1 预裂纹周围的压缩残留应力分布

预裂纹的长度a≅3 mm，回火裂纹和疲劳裂纹周围的压缩残留应力σr的分布的测量结果如图6所示.图6中的横坐标x是裂纹中心算起的裂纹的单向长度.另外压缩残留应力是在图2所示的实验片被加工下来以后，测量的与裂纹相垂直方向的结果.由图6中的结果可知，沿着整个的回火前的疲劳裂纹，都明显地存在有压缩残留应力，特别是在裂纹的端部σr的值更大;但是裂纹回火后，即使是在裂纹的端部，σr的值基本消失.

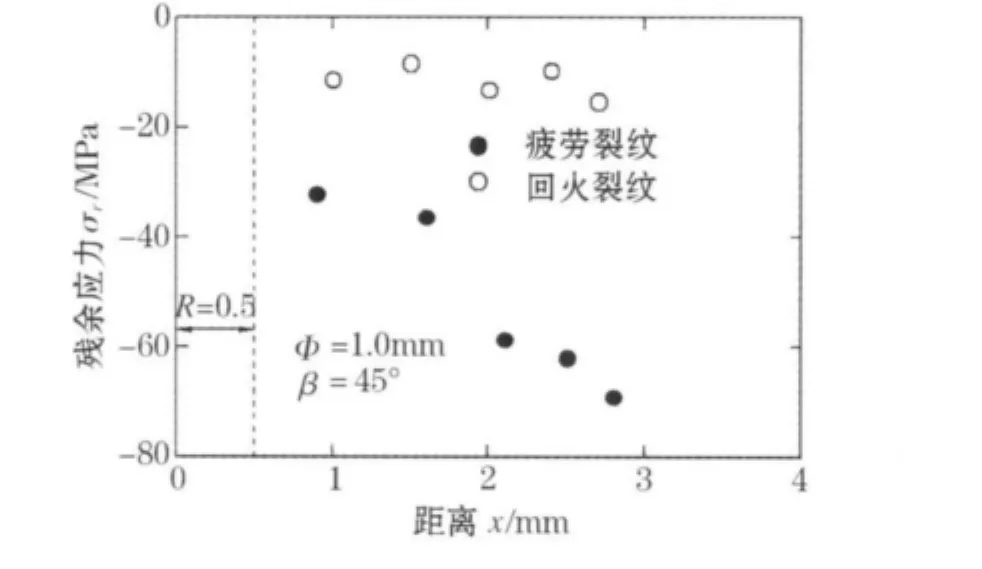
图6 沿着疲劳和回火裂纹的压缩残留应力

2.2 裂纹的不连续位移量的测定结果

长度a≅3 mm的疲劳和回火预裂纹，在应力σ=120 MPa的情况下测得的裂纹开口方向和滑移方向的位移量如图7所示.图7中的虚线是按下面的公式2计算的理论值.

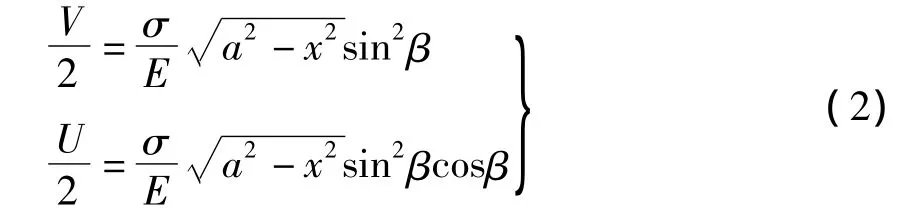
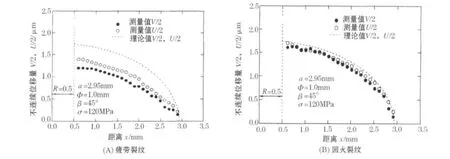
图7 沿着裂纹的不连续变位量的测量结果

a为单侧预裂纹的长度，x为从裂纹中心算起的距离，E=205.8 GPa为实验材料的弹性模量.由于倾斜角β=45°，所以图中理论值的V/2与U/2相重合.

对于疲劳裂纹，由于压缩应力和裂纹表面相互接触的影响，开口方向的变位量V/2和滑移方向的变位量U/2的实测值都小于理论值.但回火后的裂纹两者的实验值与理论计算值相当接近.

2.3 应力扩大系数

预裂纹端部的应力扩大系数按公式(2)计算.式中的r为从裂纹端部算起的距离.由公式(2)理论值的V/2和U/2算出的Ⅰ型和Ⅱ型应力扩大系数表示为KⅠ，KⅡ，由实验值计算出的应力扩大系数表示为(KⅠ)mes以及(KⅡ)mes.

当裂纹长度a≅3 mm时，由上式计算的应力扩大系数如表3所示.由该表可知，对疲劳裂纹，(KⅠ)mes以及(KⅡ)mes的实验值都比理论值小.(KⅠ)mes的降低主要是由于疲劳裂纹周围存在压缩残留应力，又因为该压缩应力是与裂纹相垂直，所以导致裂纹开口方向变形能力的降低;同时，裂纹表面呈锯齿状，在裂纹的开口不够大的情况下，上下表面间产生接触，使得裂纹在滑移方向的变形困难，导致(KⅡ)mes的减小.由于回火裂纹的周围的压缩残留应力的消失，(KⅠ)mes的结果显著地增加了;另外随着裂纹开口方向变形的增加，上下表面的接触面积也会随之减小，滑移方向变形的阻力逐渐下降，使得(KⅡ)mes增大.而且此时两者都与理论值基本相一致.

表3 预裂纹端部的应力扩大系数

3 讨论

1)曲折疲劳裂纹曲折角度的预测

当倾斜预裂纹形成曲折而继续扩展时，在扩展刚刚开始时曲折角度预测值可以用公式(4)计算.该式是由最大切线应力准则而推导出来的.将表3的应力扩大系数的理论值和实践值分别代入该式即可得到曲折角度的理论预测值θ和实验预测值θest.

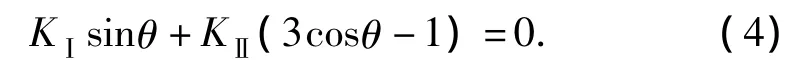
2)曲折角度的影响因素

将实验测得的曲折疲劳裂纹的曲折角度θest与以上计算的预测结果一起表示，如图8所示.由图可知，对于疲劳预裂纹θest大于θ，这与表3的结果相吻合.同时沿着曲折裂纹的全长测得的θest的结果都与θest基本一致.也就是说当预裂纹周围存在压缩残留应力时，预裂纹自身的变形行为受到制约的同时，如果裂纹在载荷的作用下继续扩展，其扩展的路线会受到来自预裂纹自身的变形特性的影响.但对于回火预裂纹，无论是计算的预测值θest还是实测值θest其分布都在θ的附近，因此可以说最大切线应力准则对预测曲折裂纹的传播路径是有效的.

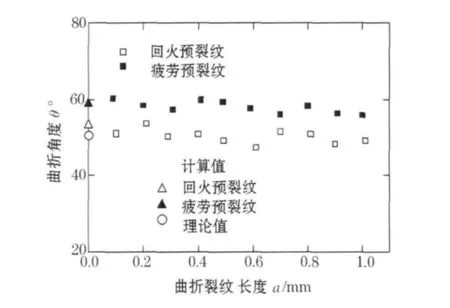
图8 曲折裂纹的曲折角度

4 结论

1)混合型疲劳预裂纹，周围存在的压缩残留应力使得裂纹端部的Ⅰ型应力扩大系数(KⅠ)mes减小;当裂纹的开口方向的变形受到制约时，由于裂纹呈锯齿形状的上下表面彼此之间的相互接触，Ⅱ型应力扩大系数(KⅡ)mes也同时降低.

2)对裂纹的滑移变形的制约作用是由于裂纹表面接触而产生的.显然裂纹表面的接触面积是随着裂纹开口方向变形的减小而增加的.所以对于有压缩残留应力的预裂纹，才会产生这种影响.而且特别在裂纹的端部这种影响更为明显.

3)自身的变形受到影响的疲劳预裂纹，在载荷的作用下继续扩展时，其扩展的路径仍然会受到影响.也就是说，实际测得的疲劳预裂纹的曲折角度θest大于用最大切线应力准则所计算的预测值θ.但对于回火预裂纹θest与θ基本相一致.

［1］YAN X，WU H.A numerical method for multiple cracks in an infinite elastic plate［J］.Journal of Harbin Institute of Technology(New Series)，2005，12(4)，351－357.

［2］于慧臣，孙燕国，张岩基，等.不锈钢在扭转/拉伸复合载荷下近门槛值的疲劳裂纹扩展行为［J］.金属学报，2006，42(2)，186－190.

［3］JONO M，SONG J H.Fracture Crack(Crack Closure and Predictions of Crack Growth Rate)［M］.Osaka:Osaka University Press，2005:27－51.

［4］SURESH S.Fatigue crack deflection and fracture surface contact:micromechanical models［J］.Metallurgical Transactions，1985(A16):249－260.

［5］HALLIDAY M D，BEEVERS C J.Some aspects of fatigue crack closure in two contrasting titanium alloys［J］.Journal of Testing and Evaluation，1981，9(4):195－201.

［6］SURESH S，RICHIE R O.A geometric model for fatigue crack closure induced by fracture surface roughness［J］.Metallurgical Transactions，1982(A13):1627－1631.

［7］MA Y L.Study on Fatigue crack Propagation Behavior under Mixed－Mode conditions with Compressive Residual Stress［D］.Tokyo:Okayama University，2006.

［8］OKAMURA H.Linear Fracture Mechanics［M］.Tokyo:Baihuu－kan，2002，15－25.