锁相环小数N分频频率综合器中的Sigma-delta调制器设计

吴小林，朱学勇，文光俊

（电子科技大学 通信与信息工程学院 射频集成电路与系统研究中心，四川 成都 611731）

0 引言

随着锁相环频率综合器的广泛应用，不同的应用要求也产生了不同的综合器结构，如整数分频环、分数分频环、单环路、多环路等。整数分频频率综合器的频率分辨力就是参考时钟的频率。小数N分频频率综合器就是分频系数N是小数，而不再是整数。小数N分频频率综合器最大的特点就是能兼顾相位噪声和系统速度的要求，特别是针对相位噪声要求不是特别高，但对频率分辨力和环路频率切换速度要求高[1]。

基于一阶的Sigma-delta调制器的频率综合器由于小数毛刺的影响很难在实际产品中得到应用，故通过将一阶Sigma-delta级联，就可以构成新的小数N分频频率综合器（N为小数）。级联的高阶Sigma-delta调制器可以将噪声推向高频处，再通过频率综合器中的环路滤波器进行低通滤波，滤掉高频噪声，从而达到噪声整形的目的。同时，为了避免稳定性的问题而又能得到高阶的噪声整形性能，可以通过对一阶和二阶的调制器进行级联的方式来实现，这就是所谓的Mash（MultiStage Noise⁃shaPins）型调制器结构[1]。本文采用3个一阶调制器级联的方式，构成三阶的Sigma-delta调制器，称作MASH1-1-1结构[2]。在实现其具体电路时采用Verilog HDL硬件描述语言编写MASH1-1-1结构的代码，在modelSim SE 6.2b中通过了功能仿真并在XUP Virtex-II Pro FPGA开发板上进行了验证，最终采用TSMC 0.13 μm CMOS工艺，完成了电路版图。

1 锁相环小数N分频频率综合器

锁相环小数N分频频率综合器的总体电路图如图1所示，图中为全差分结构。其工作原理是：1）鉴频鉴相器（Phase Frequency Detector，PFD）对外部输入的参考频率Fref与锁相环内分频器输出频率Fd进行相位和频率的比较。只要Fref与Fd之间有频差和相位差，鉴频鉴相器就根据该差值输出脉冲信号直接作用于电荷泵。2）电荷泵（CP）根据前级PFD的输出脉冲信号，控制后级的环路滤波器（Loop Filter，LPF）进行充电或者放电，以改变输出电压Vc的值。3）Vc控制压控振荡器（Voltage Controlled Oscillator，VCO）的输出频率FVCO，使得FVCO经N/N+1双模分频器分频后的输出信号Fd的频率和相位朝着更加接近Fref的方向变化。通过不断的反复调整，最终使Fd和Fref同频同相。Vc稳定之后，VCO输出稳定的FVCO，达到锁定状态[2]。

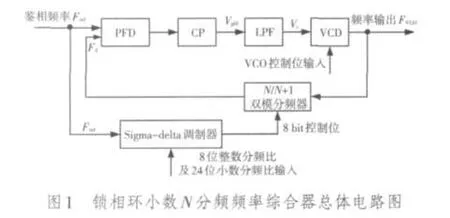
在图1中，双模N/N+1分频器在k个参考时钟周期内是N+1分频，而在L-k个参考时钟周期内是N分频的，则在 L个参考时钟周期内对VCO的平均分频比为((N+1)×k+N×(L-k))L=N+k/L，因此综合器的分辨力能达到Fref/L，这样参考时钟就能取得比较高，环路的响应速度随着环路带宽的增加而提高[3]。

在本项目中，参考频率为Fref=20 MHz，频率综合器输出频率FVCO=2 200～4 000 MHz，设分频器的分频比为N·f，则整数分频比N取值范围N=FVCO/Fref为110～200，小数分频比f取值范围在0～1之间的小数。所采用的双模N/N+1分频器的结构图如图2所示。

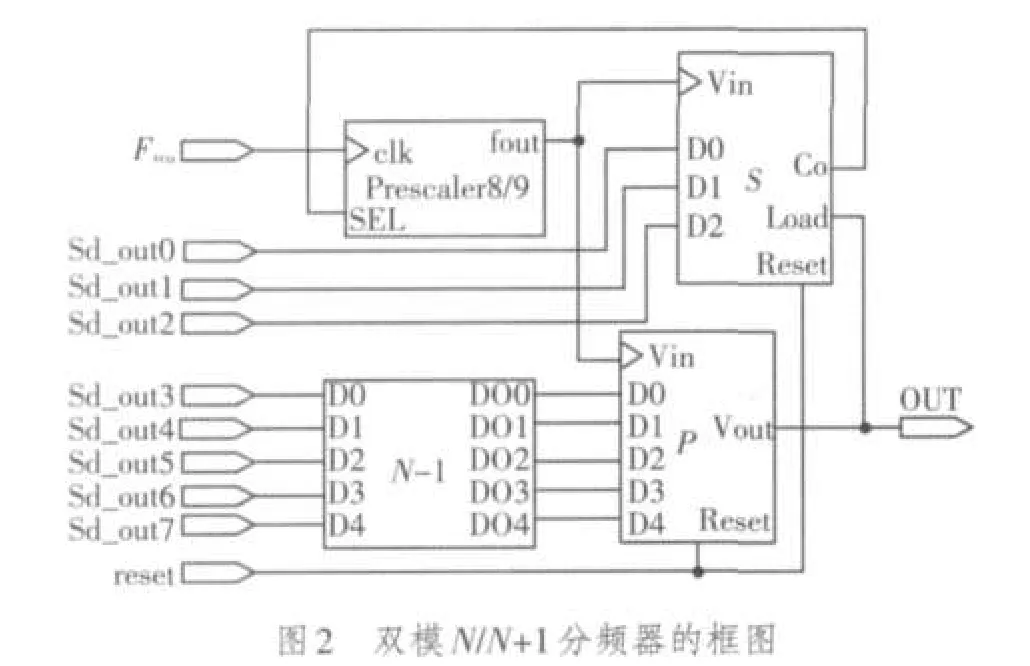
要实现分频比为110～200，高速预分频器采用8/9分频；程序计数器P取5位二进制位，取值范围为13～26；对于MASH1-1-1结构的三阶Sigma-delta调制器，其输出为3位，即只有分频比的低3位会受到调制器输出的调制，故吞脉冲计数器S取3位，取值范围为0～7。这样，整数分频部分的分频比为104（13×8）～215（26×8+7），覆盖了110～200。

双模N/N+1分频器的具体工作原理如下：将Sig⁃ma-delta调制器的8位输出sd_out输入到分频器，给分频器置数。Sigma-delta调制器输出的低3位直接输入到S分频器，给S分频器置数；高5位通过N-1解码器将数字减1，然后给P计数器置数。其具体工作流程如下：开始8/9预分频器处于低模状态（9分频），输入信号FVCO经过9分频由fOUT输出，计数器S和计数器P同时对fOUT计数。由于P>S，当fOUT输出第S个脉冲后，S计数器递减为0，S计数器的输出CO端由低电平变为高电平，8/9预分频器变为高模状态（8分频），P计数器继续计数，当计满（P-S）个脉冲后，P计数器回0，输出端VOUT输出一个低脉冲，使8/9预分频器回到低模状态，S计数器和P计数器复位重新回到初始状态，重新置数，开始下一次新循环。

8/9预分频器进行了S次9分频，（P-S）次8分频，总的分频比为8P+S。8P代表的分频比的整数部分，P计数器的初始值设置为sd_out[7:3]-1；S代表分频比的小数部分，由Sigma-delta调制器的输出的第3位进行调制，故S计数器的初始值设置为sd_out[2:0]。最终，分频器的分频比设置为8*sd_out[7:3]+sd_out[2:0]-8。

2 Sigma-delta调制器的工作原理

2.1 一阶Sigma-delta调制器

由于一阶Sigma-delta调制器与一阶相位累加器的数学模型相同，因此可采用一阶相位累加器来实现一阶Sigma-delta调制器，如图3所示。在建立一阶累加器的模型时，模型应包括其整个工作过程，如累加、进位等。每当有进位产生时必须从和中减去1，设x（n）为累加器的输入信号，s（n）为其和数，c（n）为进位，e（n）为误差信号。其模型如图3a中所示[2]。

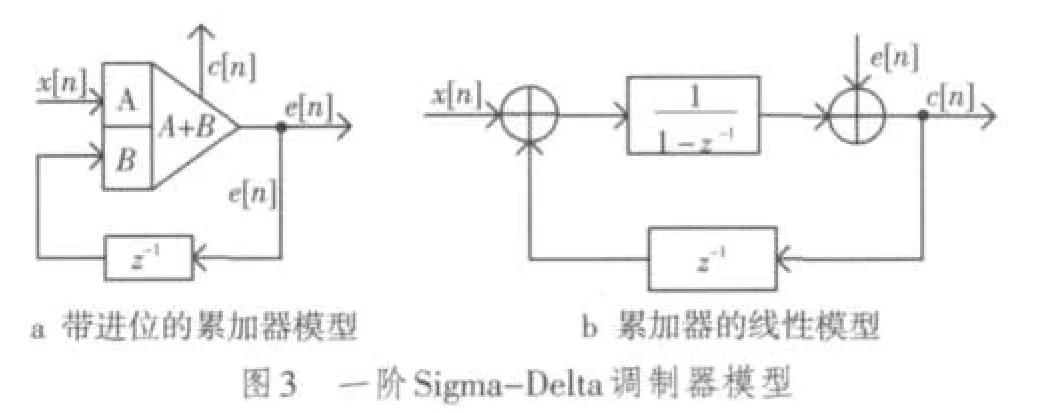
图3b是图3a的线性模型，基于线性化的模型，推导出传输函数为

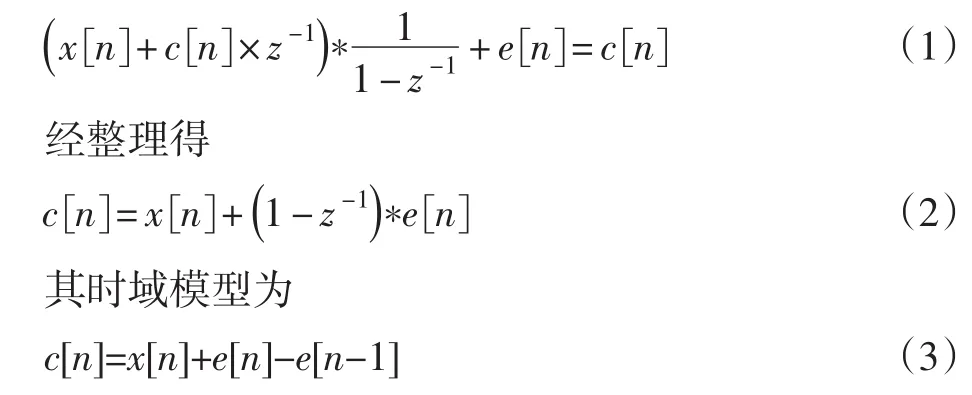
从该传输函数可以看出，(1-z-1)项对量化噪声呈现出高通特性。输出序列c[n]等于输入x[n]加上经整形后的量化噪声。该序列的一个重要的特性就是其输出噪声的频谱集中于高频处，这样就可以通过一个低通滤波器很容易地将噪声滤除。这就是噪声整形的原理。

2.2 MASH1-1-1 Sigma-delta调制器

图4所示为MASH1-1-1结构的Sigma-delta调制器。它是由3个一阶累加器级联而成。图中的延迟单元是采用D触发器来实现，由参考频率Fref作为其时钟。

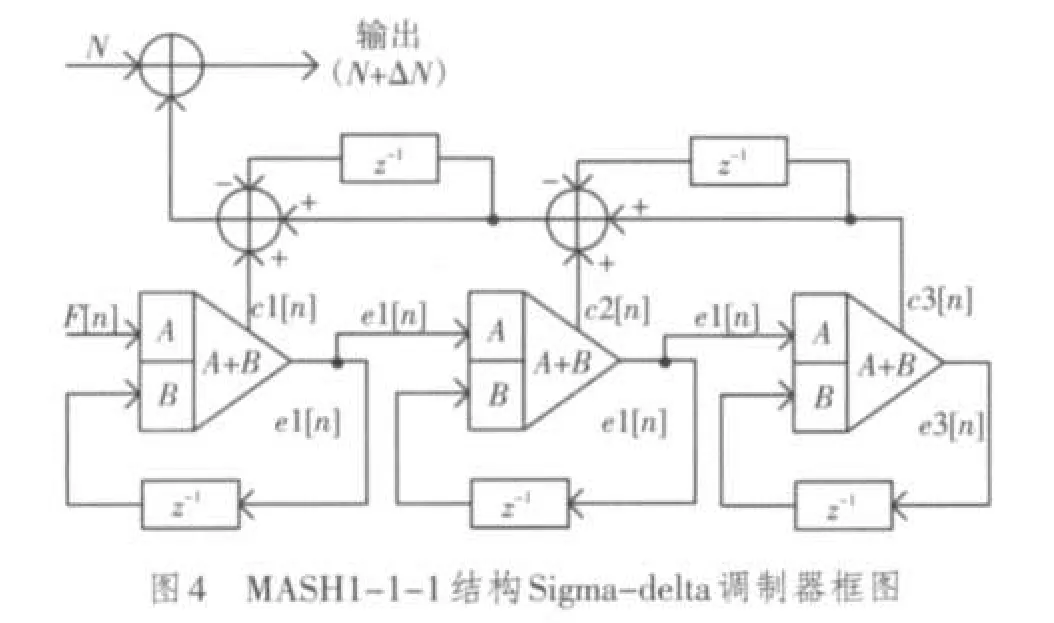
MASH1-1-1结构中，各个累加器的进位输出函数为

输出ΔN[n]等于输入F[n]加上最后一级的量化噪声。从ΔN[n]的表达式可以明显看出，后面各级可以抵消前级的噪声贡献，只剩下最后一级的噪声。但是这个噪声是经过（1-z-1）3高通项整形后的噪声，其频谱被更大程度地挤压到高频端，因而对噪声的整形效果更好。

调制器的输出ΔN[n]的平均值为f=F/2M，M为累加器的模数，即数字Sigma-delta调制器的比特数。当输入F[n]为一个常数值时，第一个累加器每2M个时钟周期会产生F[n]次进位，所以ΔN[n]的平均值为F/2M，其他累加器的进位输出的长期贡献为零，只是起噪声整形的作用。参考频率为Fref=20 MHz，故M取24时，可得到频率综合器的分辨力为20 MHz/224=1.2 Hz[4]。

对于3阶MASH1-1-1结构的Sigma-delta调制器而言，ΔN只能取-3～4之间的8个整数值，但经过低通滤波后输出可以达到非常高的分辨力。通过与整数分频比N相加，使输出的分频比取N-3和N+4之间的一系列整数值，然后通过在一段时间里取平均，最终得到需要的小数分频比。

3 Sigma-delta调制器的生成版图

当整数分频比N=150，小数分频比f=0.5时，程序得到的仿真图如图5所示。在第一个光标处，sd_rst为1，系统进行复位，之后的一个sd_clk的上升沿，sd_rst为0，系统开始工作。但因为数字系统本身存在的延时，此时输出的sd_out是不正确的，直到第二个光标处。第二个光标之后的sd_clk的上升沿，调制器开始正常工作，并以8个 sd_clk为周期，sd_out循环输出 150，150，151，153，149，148，152，151这8个值，且（150×2+151×2+153+149+148+152）/8=1 204/8=150.5，符合要求的分频比。

如上所示，Sigma-delta调制器的一个问题是当输入为2的负整数次方或这些负整数次方的和差时（例如0.25，0.5，0.75等），输出端就会出现有限循环问题[5]，从而导致在频域中出现毛刺，出现这种现象的原因是这些二进制数字缺乏随机性。这种毛刺也会恶化频率综合器的总体相位噪声特性。

基于TSMC 0.13 μm CMOS工艺，完成的Sigma-delta调制器的版图如图6所示。该版图经过了DRC和LVS验证，可应用在锁相环小数N分频频率综合器中。

4 结果分析

对Sigma-delta调制器的版图进行SPICE仿真，可观察到在刚开始工作时，输出的平均电流（VDD）不稳定，最大可以为-1.81 mA，如图7所示。在稳定工作后，如在2 ns之后，平均电流（VDD）稳定在-883～-892 μA之间，乘以电压（VDD）1.2 V，可以计算出平均功耗在1.059 6～1.070 4 mW之间，如图8所示。

5 小结

本论文讲述了应用于锁相环小数N分频频率综合器中的Sigma-delta调制器的设计，并结合多模分频器介绍了其工作过程。设计版图与锁相环小数N分频频率综合器的联合仿真符合项目的要求。

[1]RHEE W，SONG B S，AKBAR A.A 1.1 GHz CMOS fractional-N frequency synthesizer with a 3-b third-orderΔ-Σmodulator[J].IEEE Journal of Solid-State Circuits，2000，35（10）：1453-1460.

[2]刘愿.基于Sigma-delta调制器的小数N频率综合器设计[D].西安：西安电子科技大学，2009.

[3]何捷.DVB-T接收机中频率综合器的研究[D].上海：复旦大学，2005.

[4]YANG Yuche，YU Shihan，LIU Yuhsuan.A quantization noise suppression technique for Δ∑fractional-N frequency synthesizers[J].IEEE Journal of Solid-state Circuits，2006，41（11）：2500-2511.

[5]BOURDI T.A Delta-sigma frequency synthesizer with enhanced phase noise performance[EB/OL].[2010-10-15].http：//ieeexplore.ieee.org/search/freesrchabstract.jsp?tp=&arnumber=1006847&queryText%3DBOURDI+T.+A+Delta-Sigma+frequency+synthesizer+with+enhanced+phase+noise+performance%26openedRefinements%3D*%26filter%3DAND%28NOT%284283010803%29%29%26searchField%3DSearch+All.