近自由面三维水翼的水动力分析及试验研究
2011-06-07陈庆任叶恒奎杨向晖冯大奎管延敏
陈庆任,叶恒奎,杨向晖,冯大奎,管延敏
(1华中科技大学船舶与海洋工程学院,武汉 430074;2中国舰船研究设计中心,武汉430064)
1 引 言
由于水翼已经在水翼复合船、滑行艇和两栖战车等交通工具上得到了广泛的应用[1-4],因而研究三维水翼的水动力性能是非常必要的,其中,自由面对水翼性能的影响是不可忽视的。研究分析不同航速下水翼的性能以及水翼与船体间的相互影响,对水翼的实际应用有重要的意义。
国际上,Park和Chun[5]使用一种高阶边界元法对三维翼绕流进行了计算,Xie和Vassalos[6]基于势流理论应用面元法对带自由面三维水翼进行了研究。在国内,汪淳和邹早建[7]利用Rankine奇点面元法计算了三维水翼的定常升力绕流,张利军和王言英[8]应用低阶速度势面元法对三维水翼水动力性能进行了预报。李国安和叶恒奎[9]采用三维时域格林函数法对近水面水翼影响下的船体兴波进行了研究分析。
本文基于格林定理,将边界元法应用于近自由面三维组合翼的水动力分析,考虑了中间的支柱翼与两边控制翼之间的相互影响,对两种翼型在不同浸深、航速和攻角下的升阻力特性进行了计算,并进行了试验研究。其中,在自由面采用非线性自由面边界条件,对中间支柱翼周围自由面网格采用割划网格技术;在尾涡面上采用时间步进法及尾涡存储效应以满足尾缘的Kutta条件。由于水翼尾部很薄,计算所布置的奇点很接近,本文影响系数中的奇异积分及非奇异积分都采用精确积分的方法计算,这是一种确保计算精度的有效方法。
2 理论公式
根据势流理论,假定流域为不可压无旋的理想流体,定义边界S包围的流场区域V,S由机翼表面SB、自由表面SF及尾涡面SW组成,见图1(其中SF只显示半边)。

图1 计算边界及坐标系示意图(其中SF只显示半边)Fig.1 Boundary condition and coordinate system
当场点P( x,y,z)位于边界面S上时,格林定理可以描述为[10]:

(1)式可展开写成

在物面SB上根据不可穿透物界条件,可得物面SB的运动学边界条件:

自由表面SF的动力学边界条件和运动学边界条件可以表示为[11]:

式中,g为重力加速度,η为自由表面形状。
Kutta条件要求尾缘处速度为有限[12]:

初始条件为:

3 数值方法
对边界面进行单元离散,水翼表面SB可以划分为NB个单元,自由表面SF划分为NF个单元,尾涡面SW划分为NW个单元,依次编号为Ni(i=1,2,3,…,NB+NF+NW)。 相应地,把场点P( xi,yi,zi)和源点Q(xj,yj,zj)分别置于每个单元的形心处,则(2)式可离散化写成
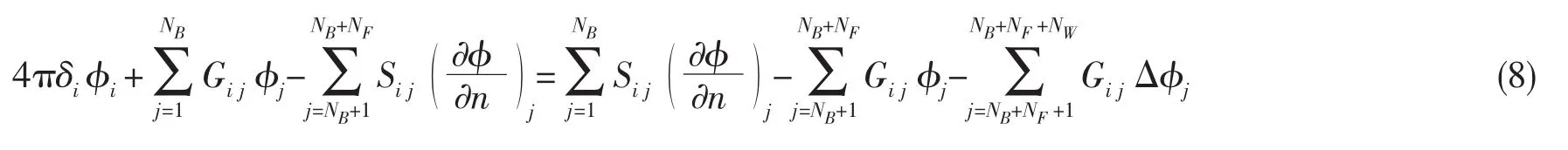
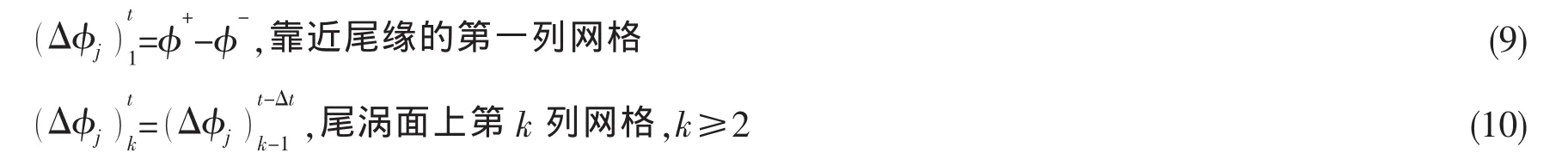
式中,φ+、φ-分别为水翼尾缘上、下单元的瞬时速度势。
利用物面条件(3)和初始条件(7)求解方程(8)可以得到初始时刻翼面上的速度势和自由面上的法向速度,由(4)、(5)式求得波高和新生成的自由面的势,同时由(9)、(10)式可更新得到尾涡面上新的偶极子Δφj。这样,即可进行下一时刻的求解,经过不断迭代计算,直到波形稳定,结束计算。
由(8)式可以得到翼面上单元节点的速度势,
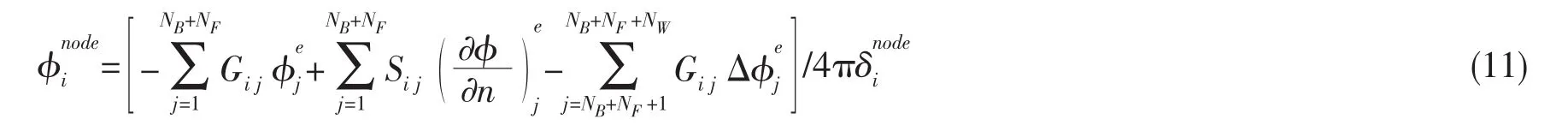
则利用有限元插值法对翼面单元进行计算可以得到其速度分布[13],进一步由伯努利方程求得压力分布,

再通过积分可以求出水翼所受的阻力D和升力L,定义兴波阻力系数和升力系数为

式中,SC为水翼的水平面积,Sc=cl(c为水翼弦长,l为水翼展长)。
4 试验及数值计算结果分析
4.1 试验介绍
试验的研究重点是测试选定的三维翼在不同浸深、不同航速和不同攻角下近水面航行时的水动力特性。试验在拖曳水池中进行,试验设备主要由机械系统、电气系统、信号采集和处理系统等组成。图2显示了试验设备中的机械系统,其中两边是研究选用的控制翼,中间是一个支柱翼,起支撑和导流作用。
本次试验中,采用了两种控制翼面:梯形翼(展弦比 λ=2,尖梢比 Tr=0.45,后掠角 αs=0)和矩形翼(展弦比 λ=2.5),翼型均为 NACA0015。支柱翼翼型采用NACA0012。
4.2 梯形翼数值计算结果
梯形翼平均弦长为145mm,试验测试了两个浸深,分别为d=250mm和d=117mm,两个航速,即V=0.5m/s和 V=1.0m/s。
建立类似图1的计算网格,对不同浸深、不同航速和不同攻角下的近水面水翼的水动力性能进行了计算,将所得的升力系数CL与试验数据进行了对比。图3、4为深浸深的结果对比,可以发现两者取得了很好的吻合;图5、6给出了浅浸深的结果对比,两者的趋势基本吻合。由于大攻角下绕水翼流动将产生分离,数值计算结果在大攻角时均存在较大误差。
图7、8分别给出了d=250mm、V=1.0m/s、攻角α=5°下水翼表面的速度势分布和压力分布。

图2 试验设备图(机械系统)Fig.2 Mechanical system of test equipments

图3 d=250mm、V=0.5m/s下的结果对比Fig.3 Comparison of lift forcing coefficient at d=250mm,V=0.5m/s

图4 d=250mm、V=1.0m/s下的结果对比Fig.4 Comparison of lift forcing coefficient at d=250mm,V=1.0m/s

图5 d=117mm、V=0.5m/s下的结果对比Fig.5 Comparison of lift forcing coefficient at d=117mm,V=0.5m/s

图6 d=117mm、V=1.0m/s下的结果对比Fig.6 Comparison of lift forcing coefficient at d=117mm,V=1.0m/s

图7 水翼表面的速度势分布(d=250mm、V=1.0m/s、α=5°)Fig.7 The potential distribution on hydrofoil(d=250mm,V=1.0m/s,α=5°)

图8 水翼表面的压力分布(d=250mm、V=1.0m/s、α=5°)Fig.8 Pressure distribution on hydrofoil(d=250mm,V=1.0m/s,α=5°)
4.3 矩形翼数值计算结果
矩形翼弦长为160mm,试验测试了一个浸深为 d=182mm,3 个航速,即 V=0.5m/s、V=1.0m/s和V=1.5m/s。
建立如图1的计算网格,对不同航速、不同攻角下的近水面水翼的水动力性能进行了计算,将所得的升力系数CL及阻力系数Cd与试验数据进行了对比,见图9、10和11。可以看出,两者的趋势基本吻合,其中V=0.5m/s下的CL吻合得很好,V=1.0m/s、1.5m/s则在大攻角时存在较大误差。

图9 V=0.5m/s下的结果对比Fig.9 Comparison of resistance and lift forcing coefficient at V=0.5m/s

图10 V=1.0m/s下的结果对比Fig.10 Comparison of resistance and lift forcing coefficient at V=1.0m/s

图11 V=1.5m/s下的结果对比Fig.11 Comparison of resistance and lift forcing coefficient at V=1.5m/s

图 12 V=1.5m/s,控制翼攻角 α=0°Fig.12 Comparison of wave pattern at V=1.5m/s,α=0°

图 13 V=1.5m/s,控制翼攻角 α=-5.0°Fig.13 Comparison of wave pattern at V=1.5m/s,α=-5.0°
分析水翼对主船体的兴波影响对水翼的实际应用是有重要意义的,本文分别计算了组合翼及单个支柱翼的兴波,并进行了对比,见图12、13,其中上半图(Y+)为组合翼兴波图,下半图(Y-)为单翼兴波图。
从图12可以看出,当控制翼攻角α=0°时,支柱翼后的波峰与波谷都增大了。由图13可以看出,当控制翼攻角α=-5.0°时,支柱翼后波谷较平。
5 结 论
本文基于格林定理,运用边界元法、时间步进法求解了近自由面条件下的三维组合翼的势流场,通过理论计算和试验研究的对比,可得出如下的结论:
(1)本文对组合翼水动力性能进行了计算,数值结果与试验结果的比较说明了所开发的计算程序结构合理,结果具有可靠性。文中的数值方法和研究工作为进一步深入研究水翼性能和优化设计打下了基础。
(2)文中所构建的考虑自由面的时域计算模型和方法是可行的,可进一步应用于近水面振动翼运动、水翼船兴波等问题的求解。
[1]王献孚.船用翼理论[M].北京:国防工业出版社,1998.
[2]Tarafder M S,Suzuki K.Computation of wave-making resistance of a catamaran in deep water using a potential-based panel method[J].Ocean Engineering,2007,34(3):1892-1900.
[3]Ciortan C,Wanderley J,Guedes S C.Turbulent free-surface flow around a Wigley hull using the slightly compressible flow formulation[J].Ocean Engineering,2007,34(10):1383-1392.
[4]Singh S P,Sen D.A comparative linear and nonlinear ship motion study using 3-D time domain methods[J].Ocean Engineering,2007,34(13):1863-1881.
[5]Park I K,Chun H H,et al.Free surface flow analysis around three dimensional hydrofoils by a higher order boundary element method[C]//Proceedings of China-Korea Marine Hydrodynamics Meeting.Shanghai,China,1997.
[6]Xie N,Vassalos D.Performance analysis of 3D hydrofoil under free surface[J].Ocean Engineering,2007,34:1257-1264.
[7]Wang Chun,Zou Zaojian.A 3D panel method for hydrodynamic forces on hydrofoils[J].Journal of Ship Mechanics,2001,5(3):18-25.
[8]张利军,王言英.基于B样条网格的三维水翼水动力性能研究[J].水动力学研究与进展,2006,21(3):381-387.
[9]李国安,叶恒奎.近水面水翼影响的船舶兴波时域计算研究[J].船舶力学,2006,10(1):43-53.
[10]Kohansal A R,Ghassemi H.A numerical modeling of hydrodynamic characteristics of various planing hull forms[J].O-cean Engineering,2010,37:498-510.
[11]Ducoin A,Astolfi J A,et al.Computational and experimental investigation of flow over a transient pitching hydrofoil[J].European Journal of Mechanics B/Fluids,2009,28:728-743.
[12]Newman J N.Marine hydrodynamics[M].Cambridge,USA:The MIT Press,1977.
[13]Yang Xianghui,Ye Hengkui,et al.Computational research on wave making of moving Wigley hull in time domain[J].Journal of Hydrodynamics,Ser.B,2008,20(4):469-476.
