基于分阶段粒子群优化算法的船舶横向运动水动力参数辨识
2011-06-07戴运桃刘利强
戴运桃,刘利强,李 英
(哈尔滨工程大学 a.理学院;b.自动化学院,哈尔滨 150001)
1 引 言
船舶运动模型参数对船舶减摇、操纵等都有着重要影响。目前有很多方法用来估计水动力参数,例如切片理论[1]、细长船理论[2]、半经验主义[3]以及最近流行的参数辨识理论[4]。在1992年,Haddara等[5]从自由响应中获得随机衰减信号,并结合神经网络技术,对横摇单个自由度参数进行辨识,并将其扩展应用到横荡和艏摇耦合的方程[6]问题以及升沉和纵摇的耦合方程[7-8]参数辨识问题中。以上文献主要针对单个自由度或两个自由度的参数进行辨识,而船舶横向三个自由度的运动参数共有18个,各参数之间互相耦合,很难用理论计算或实验的方法准确获得全部参数,另外,在利用算法进行辨识时,过高的维数也会影响辨识精度。粒子群优化算法(Particle Swarm Optimization,PSO)[9-10]的基本思想是模拟自然界的鸟群行为来构造随机优化算法。通过大量实验证明其有较好的全局收敛性和稳定性,能求得常规辨识算法所不易获得的最佳参数估计。更重要的是由于PSO算法不用计算导数,对复杂的非线性模型方程是否连续,可微等都不作要求,并可以有效利用定性的专家经验,提高辨识精度和速度,因此算法简单通用,很容易被推广到高维、非定常的复杂水动力参数辨识问题上去,具有良好的工程实用价值[11-12]。本文将船舶横向运动的水动力参数辨识问题转化为优化问题,分析各水动力参数的敏感度特性,找出起重要作用并且灵敏度较高的若干主要参数,以及敏感度低的参数,利用分阶段PSO算法寻找最优参数,提高计算效率和辨识精度。仿真试验证明,该方法能够直接有效地辨识出船舶横向运动参数。
2 船舶横向运动数学模型
2.1 状态方程
根据船舶水动力理论[13],基于切片理论,把围绕细长船体的三维流动近似简化为绕各横截面的二维流动,求得横截面遭受的流体作用力后,再沿船长方向积分迭加,并经海浪谱加权平均的船舶横向运动的简化方程如公式(1)所示。
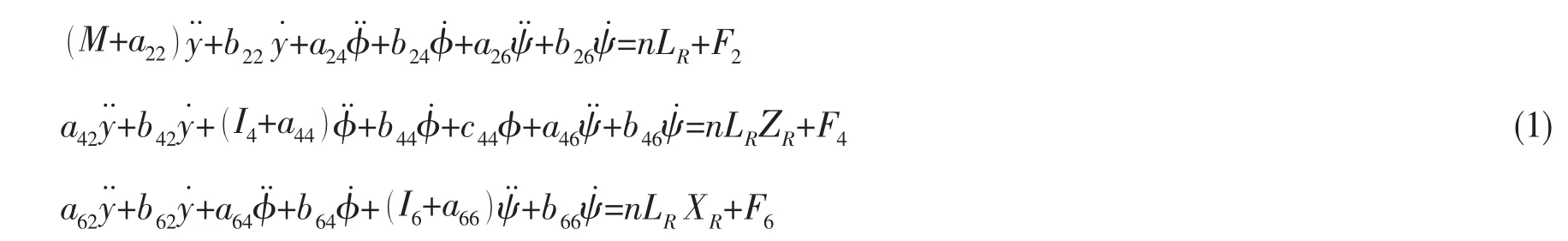
式中:y为横荡位移,φ为横摇角,ψ为艏摇角,M为船体质量,I4,I6分别为船体的质量对x,z轴的惯性矩,aij(i, j= 2,4,6)为附连质量或附连质量惯性矩,bij(i, j= 2,4,6)为与运动速度或角速度相联系的阻尼系数,c44为静水力恢复系数,F2,F4,F6分别为横荡扰动力,横摇扰动力矩和艏摇扰动力矩,n为舵的个数,LR为水平舵力,ZR是舵力中心至重心的垂向距离,XR为航向舵舵力中心至重心的横向距离。
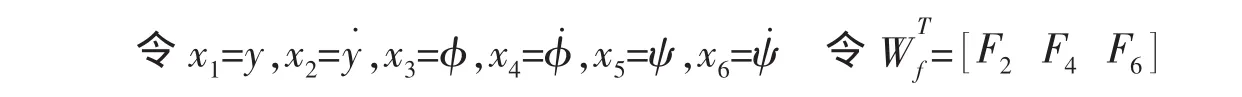
并设状态变量为

则得到系统状态方程如下:
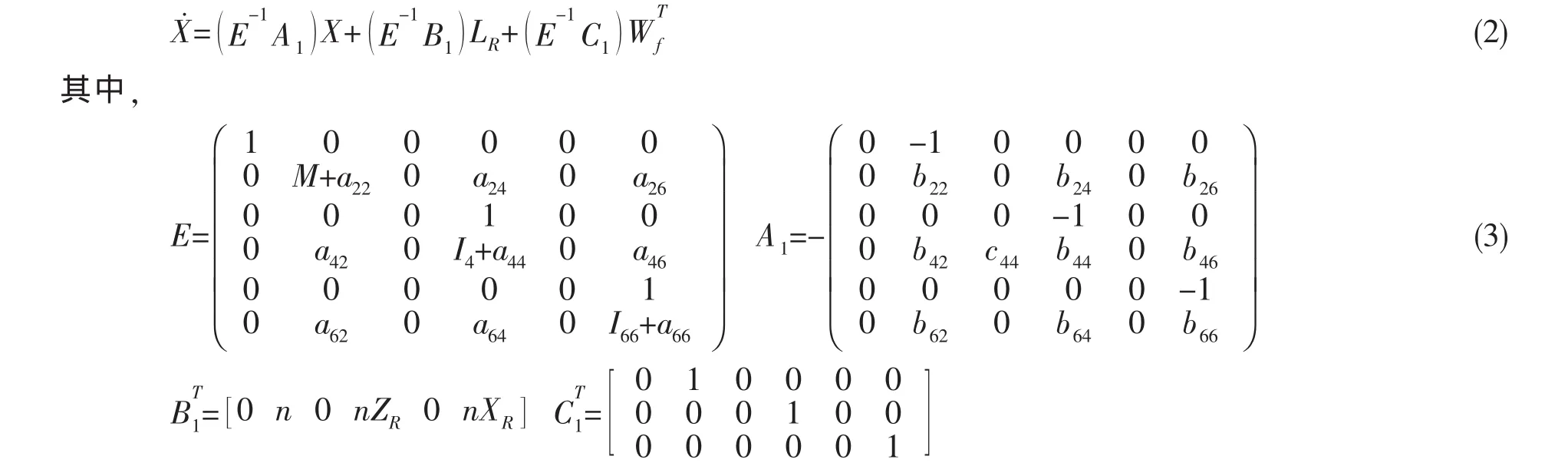
2.2 观测方程
若选择横荡位移y,横摇角φ,艏摇角ψ作为观测量,则

Y=[y φ ψ ]T为观测向量,V为三维测量噪声,通常情况下可以认为是白噪声,它的方差阵按一级精度的传感器可以取为Qvv=diag[2.03*10-32.25*10-72.25*10-7]。
3 基本粒子群优化算法
1995年,Kennedy和Eberhart给出了最早的粒子群优化算法。在算法中,每个个体称为一个“粒子”,每个粒子代表着一个潜在的解。在连续空间坐标中,粒子群优化算法描述如下[9-10]:
设搜索空间为D维,N个粒子组成一个群落,第i个粒子 (i= 1 ,2,…,N)位置为xi=(xi1,xi2,…xiD)T,第i个粒子的速度为向量vi=(vi1,vi2,…viD)T,每个粒子在当前位置处的适应度值(衡量粒子优劣的函数的值)fitnessi=fitness( xi),其对应的自身最优值为Pi=(Pi1,Pi2,…PiD),种群当前最优经验值记为Pg=(Pg1,Pg2,…PgD)。各粒子根据对个体和种群的飞行经验的综合分析来动态调整个体自身的飞行速度,同时向着自己以前经历过的最好位置和其它微粒曾经经历过的最好位置飞行。各粒子按公式(5)来进行自身速度和位置的更新。

其中:t为迭代次数,d=1,2,…,D。r1,r2为[0,1]范围内变化的随机数,c1,c2为非负常数,称作学习因子,用以调节每次迭代的步长。
4 基于分阶段粒子群优化的船舶横向运动参数辨识
4.1 算法基本思想
船舶横向运动参数辨识问题的难点在于模型中参数空间维数为18维,各参数本身之间也是高度耦合的。一般来说,参数越多或参数间非线性越强,则拟合时间越长,拟合的精度也越差,另外也越不能够保证拟合算法能够收敛到整体最优。参数拟合理论已经证明[14]:利用实验数据仅对一个未知参数进行拟合是比较容易实现的,但是如果要同时拟合多个参数,则必须考虑参数对模型的灵敏性和参数之间相关性的问题。
粒子群优化算法具有记忆微粒最佳位置的能力,因此,在利用粒子群优化算法对参数进行辨识的过程中,粒子寻优的总体原则是向着适应值小的方向进行。在这种原则下,利用粒子群算法对参数进行辨识的过程中,对适应值影响较大的参数容易收敛,而对适应值影响较小的参数往往需要更多的迭代次数才能收敛。因此,可以根据待辨识参数对适应值的影响进行分组,采用分阶段搜索方式对参数进行寻优,这样可以减少迭代次数,提高收敛速度。
4.2 参数敏感性分析方法
各水动力参数的变化对船舶各自由度的运动的影响程度不一样,为了表示船舶运动对水动力参数的敏感程度的影响,引入水动力系数敏感性指数S,定义如下:

在上式中,P代表水动力参数,R表示船舶各自由度的运动,例如横荡位移、横摇角、艏摇角等。上标“*”表示基准的水动力系数以及对应的横荡位移、横摇角和艏摇角。
从上式可以得到,敏感性指数S越大,则表示船舶在该自由度上的运动对于水动力参数的变化越敏感。
考察每一个参数的每一个采样点输入时,各参数的适应值函数的变化。输入参数设置在各参数±100%的范围内波动,并将其等间隔划分为10份。适应值函数设置如下:

j摇角误差平方和、艏摇角误差平方和加权累加后得到的即为每一个采样点的误差。经计算得到敏感性指数的计算结果见表1所示。由表 1 可得,参数 a24,b24,a44,b46,b62,b22等对总误差的适应值函数影响较大,而参数 b64,a64,a62等对总误差适应值函数影响较小,尤其是参数b64对适应值函数的变化几乎没有影响。

表1 敏感性指数Tab.1 Sensitivity coefficients
4.3 算法流程
在对参数进行辨识前,首先对参数进行分组。设定一个阈值参数T,将敏感性指数S>T的分为一组para1,而将敏感性指数S<T的分为另外一组para2,将参数分为两组进行辨识。令T=50,则分组后第一组参数为:para1= [ a22,b22,a24,b24,a26,b26,a42,b42,a44,b44,a46,b46,b62,a64,a62],第二组:para2=[b64],在对para1中参数进行辨识时,para2中参数的取值可以经验参数、船模试验得到的数据或者是用对应的搜索范围内的一个随机值,而在对第二组参数进行搜索时,将第一组搜索到的para1中各参数的最优值作为已知参数,仅对para2进行搜索。
算法的具体流程如下:
(1)对参数进行分组。依据敏感性指数将参数向量para分为两组进行辨识。
(2)完成对算法各参数的初始设置。设定群的大小、学习因子c1、c2和惯性权重w的值。
(3)第一组参数的搜索。将初始化产生的para2的值作为已知值,待辨识参数为para1中各参数。
a.生成各粒子的初始位置和初始速度;
b.计算各粒子适应度值;
c.更新个体极值和全局极值;
d.判断群体的全局极值gbest是否在设定的迭代次数alterNum内一直都不变化,如果是,则转入e,否则,转入 g;
e.变异粒子的选择及新粒子的产生[15];
对适应值排序,选择最优适应值的粒子作为变异粒子;然后根据公式(8)产生新的粒子的位置;

其中,randl为均匀分布在[0,1]之间的一个随机变量;σj为其它粒子与最优粒子位置的方差。
灵渠位于广西省桂林市兴安县,是秦始皇应军事要求而修筑的一条沟通中原与岭南的水上运输通道,至今已有两千多年的历史。灵渠现由铧嘴、大小天平、南渠、北渠、大小泄水天平和陡门等组成,设计建造科学、精巧。灵渠的修建对促进古代南北经济、文化交流及中华民族的统一做出了重要贡献,亦有“北有长城,南有灵渠”之美誉。如今,灵渠已经被列入世界文化遗产预备名单,其申报世界文化遗产的工作正在进行中。
f.更新粒子的位置和速度,并执行步骤b;
g.判断算法是否满足停止条件,若满足则输出最优结果,并执行步骤(3)第二组参数的搜索;否则,算法跳到b重复运行。
(4)第二组参数的搜索
将搜索到的para1的最优值作为已知值,仅对para2中各参数进行搜索。具体步骤同第一组参数搜索过程。满足停止条件后转入(5)。
(5)收缩para1,para2中各参数的搜索范围,将步骤(4)中辨识得到的para2的最优值作为已知值,重复步骤(3)中 a-g,搜索结束后重复步骤(4)。
(6)判断是否满足停止条件,如果不满足,重复步骤(5)。
5 仿真实验
下面以5级海情下,18kns航速,135°航向时各参数辨识结果进行分析。本次实验采用进化粒子群优化算法EPSO[15]与PSEPSO算法对横向运动参数辨识结果进行比较,两算法基本参数设置相同,各参数如下:采样数据长度N=150,粒子数m=90,c1=c2=1.496 2,惯性权重随迭代次数减少,即从初始的0.9线性递减到0.2[16],alterNum=20,ρ=0.95。各参数的搜索范围为±100%。设置最大迭代次数为1 500,PSEPSO算法与EPSO算法分别独立运行50次,算法收敛标准是连续迭代150次适应值函数改变量alter_precision<0.000 1。理论观测值使用文献中水动力参数计算得到[17]。
5级海情、18kns航速、135°航向时横向参数辨识对比结果如表2所示。

表2 5级海情、18kns航速、135°航向横向参数辨识对比Tab.2 Parameter identification result for 5 sea condition,ship speed 18kns and ship heading 135 degrees

续表2
横荡、横摇、艏摇的观测值与辨识值的比较如图1所示。
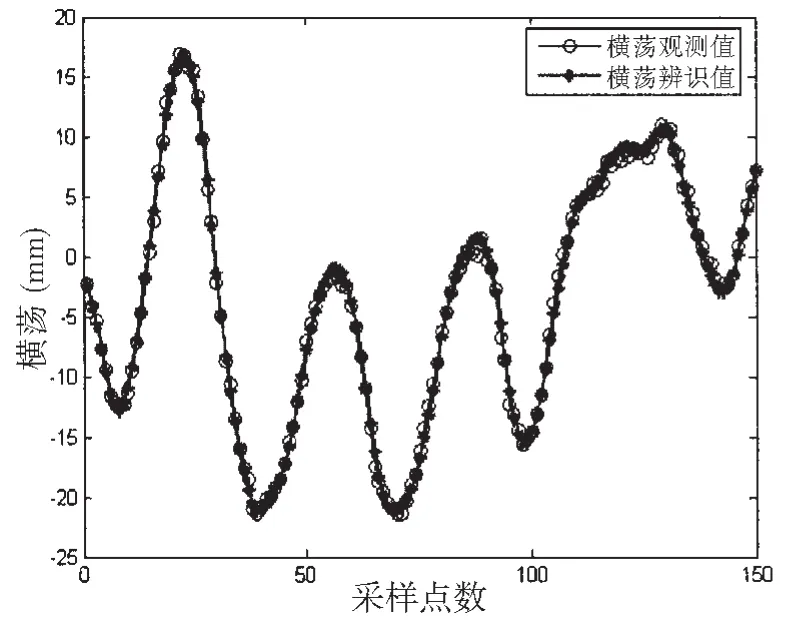
图1 (a) 横荡辨识值Fig.1(a)Identification value of sway

图1 (b)横摇辨识值Fig.1(b)Identification value of roll

图1 (c)艏摇辨识值Fig.1(c)Identification value of yaw

图2 PSEPSO与EPSO辨识收敛曲线Fig.2 Convergence curve of EPSO and PSEPSO
在图 1(a)-(c)中,横坐标是采样点数,“o”代表观测的升沉和纵摇值采样时刻的值,“*”代表模型输出的升沉和纵摇值采样时刻的值。根据辨识参数得到的模型输出值也与观测值曲线基本一致。
5级海情、18kns航速、135°航向时,在有测量噪声扰动下,PSEPSO算法与EPSO算法辨识过程中最优粒子收敛曲线如图2所示。从图上可以看到,PSEPSO算法比EPSO算法收敛更快,而且收敛的精度优于EPSO算法。
6 结 论
本文提出了一种基于分阶段粒子群优化算法的船舶横向运动参数辨识。建立了船舶横向运动状态方程和观测方程,并针对横向运动待辨识参数较多的特点,设计了一种对参数进行分类的方法,提出一种计算各参数敏感度的方法,并根据各参数的敏感度对其进行分类。最后,利用分阶段粒子群优化算法对横向运动参数进行了辨识,并对结果进行了分析。仿真结果表明,本文设计的参数辨识算法能够正确、有效地解决船舶纵向运动水动力参数辨识问题,并且本文算法的辨识精度、达优率和算法的迭代次数等都明显优于EPSO算法。
[1]Bingham H,Korsmeyer F,Newman J.Prediction of the seakeeping characteristics of ships[C]//20th Symposium on Naval Hydrodynamics.Santa Barbara,CA,1994:27-47.
[2]Wong H L.A numerical procedure for slender bodies at leeway[C]//Proc.,3rd Canadian Marine Hydrodynamics and Structures Conference.Halifax/Dartmouth,Nova Scotia,Canada.1995:62-83.
[3]Nahon M A.Simplified dynamics model for autonomous underwater vehicles[C]//Proc.,Symposium on Autonomous Underwater Vehicle Technology,1996,June 2-6.Monterey,CA,1996:373-379.
[4]Haddara M R.On the use of neural network techniques for the identification of ship stability parameters at sea[C]//Proceedings of the Fourteenth International Conference on Offshore Mechanics and Arctic Engineering.vol.II,Copenhagen,Denmark,1995:127-135.
[5]Haddara M R.On the random decrement for nonlinear rolling motion[C]//Proc.,12th International Conference on Offshore Mechanics and Arctic Engineering.Calgary,Canada,1992:283-288.
[6]Haddara M R,Wang Y.Parametric identification of coupled sway and yaw motions[C]//Proceedings of the Fifteenth International Conference on Offshore Mechanics and Arctic Engineering.vol.I,Florence,Italy,1996:267-273.
[7]Haddara M R,Xu J.On the use of random decrement in the identification of two degrees of freedom systems[C]//Proc.CSME FORUM.Ryerson Polytechnic University,Toronto,1998,May 19-22.1998(4):499-507.
[8]Haddara M R,Xu Jinsong.On the identification of ship coupled heave-pitch motions using neural networks[J].Ocean Engineering,1997,26(5):381-400.
[9]Kennedy J,Eberhart R C.Particle swarm optimization proc[C]//In:IEEE Service Center ed.IEEE International Conference on Neural Networks.Perth,Australia,995.Piscataway:IEEE Press,1995:1942-1948.
[10]Eberhart R,Kennedy J.A new optimizer using particle swarm theory[C].In:Proc of the Sixth International Symposium on Micro Machine and Human Science.Nagoya,Japan,1995:39-43.
[11]陈玮琪,颜 开,史淦君,王士同,刘志勇.水下航行体水动力参数智能辨识方法研究[J].船舶力学,2007,11(1):40-46.
[12]陈玮琪,颜 开,史淦君,鲁海燕.智能算法和物体斜出水水动力参数辨识[J].船舶力学,2008,12(2):204-210.
[13]Yu Jianxing.Modeling of multi-freedom ship motion in irregular waves with fuzzy neural networks[J].China Ocean Engineering(S0890-5487),2002,17(2):255-264.
[14]Beck J V,Arnold K J.Parameter Estimation in Engineering and Science[M].New York:Wiley,1977.
[15]戴运桃,赵希人,刘利强.基于改进粒子群优化算法的船舶纵向运动参数辨识[J].船舶力学,2010,14(1-2):44-50.
[16]Mendes R,Kennedy J.The full informed particle swarm:Simpler,maybe better[C].IEEE Transaction on Evolutionary Computation,2004,8(3):204-210.
[17]唐慧妍.船舶横向运动受扰估计、建模及LQG控制研究[D].哈尔滨工程大学,2005:185-186.
