基于随机Melnikov方法的甲板上浪船舶混沌运动研究

刘利琴，唐友刚

（天津大学 水利工程仿真与安全国家重点实验室，天津300072）

1 引 言

甲板上浪后船舶的运动非常复杂，涉及船舶的大幅非线性运动、船舶与波浪之间的非线性耦合运动以及海洋环境的随机因素。国内外学者基于数值模拟的方法研究了规则波浪中甲板上浪船舶的运动特性。Dillingham[1]最早应用浅水波理论，将甲板划分成网格，数值模拟了甲板上浪船舶的横摇、横荡耦合运动。黄祥鹿[2]将浅水波理论与切片理论相结合，在时域中分析比较了甲板上浪和无上浪两种情况船舶的横摇运动，结果表明，甲板上浪会导致具有小初稳性高的船舶倾覆。Belenky[3]基于浅水波假设，综合计算了不同甲板上浪行为时船舶的横摇运动，研究发现，甲板上浪水将增加船舶的阻尼，并引起船舶的亚谐运动。Laranjinha[4]应用随机选取法求解甲板上浪水的三维运动，数值模拟了船舶六个自由度的响应，结果表明，小量的甲板上浪水将增加船舶的阻尼，并引起船舶的亚谐运动。然而，实际海洋环境是非规则的，研究随机海浪中甲板上浪船舶的响应更具有实际意义。Yim[5]用概率密度函数研究了甲板上浪船舶的随机混沌运动，发现异宿轨道与倾覆相联系。Nakhata Tongchate[6]基于Yim的工作，在时域中数值模拟了甲板上浪船舶横摇、垂荡、纵摇耦合的三自由度响应。Troesch[7]将甲板上浪近似为一阶静水力，用概率统计的方法计算了随机波浪中船舶的非线性横摇运动，以及甲板上浪导致的倾覆问题。

本文考虑甲板上浪对船舶静稳性的影响，建立随机横浪中船舶横摇运动方程。将随机横浪激励简化为周期激励加白噪声扰动，应用随机Melnikov方法和庞加莱截面研究甲板上浪时船舶的混沌运动。

2 运动方程的建立

随机横浪中甲板上浪时船舶横摇运动的微分方程可以写为：

其中，I44为船舶横摇惯性矩；A44为附连水引起的附加惯性矩；B44为船舶横摇线性阻尼系数；B44q为船舶横摇非线性阻尼系数；Δ为船舶排水量；GZ（φ）为船舶的静稳性臂；Fsea（t）为随机横浪引起的干扰力矩；Fwod（t）为甲板上浪引起的干扰力矩。

（1）式两边除以 （I44+ A44），并将随机横浪激励简化为周期激励加白噪声扰动，有：

考虑甲板上浪对船舶静稳性的影响，（2）式进一步写为：

其中，GZm（φ）为计入甲板上浪后船舶的恢复力臂曲线。分别用x和y表示横摇角φ和横摇角速度φ˙，将（3）式写成以x和y表示的随机微分方程的典型形式为：

3 随机Melnikov方法

Melnikov函数具有简单零点，意味着稳定流行与不稳定流行在庞加莱截面上横截相交，系统出现Smale变化意义下的混沌。对于随机动力学系统，需要从统计意义上讨论随机Melnikov过程是否有简单零点，将随机Melnikov过程和均方准则相结合确定系统的混沌运动的参数域[8]，获得发生混沌时船舶的形状参数与波浪参数间的临界关系。

与方程（5）对应的无阻尼、未扰动方程为：

用-t来代替 t，（7）式可以写成：

可以看出，Md和Mp是确定量，与随机激励无关，由方程（5）的阻尼和简谐激励产生，而Z是随机过程，由方程（5）的随机噪声引起。随机Melnikov过程（8）的均值为E[ M（ t1,t2）]=-Md+Mp（t1），方差为 σ2Z，计算公式为：

对于一般的船舶，GZm（x）是关于x的高次多项式，由（6）式很难求出横摇角速度y0的解析表达式，本文采用数值法求解。由于y0是时间t（ t∈（-∞,+∞））的函数，（x0, y0）=（x0（ t）,y0（t））为同宿轨道，初始积分点q2选为同宿轨道与x轴的交点，从而y0（t）为t的奇函数。（8）式可进一步写为：

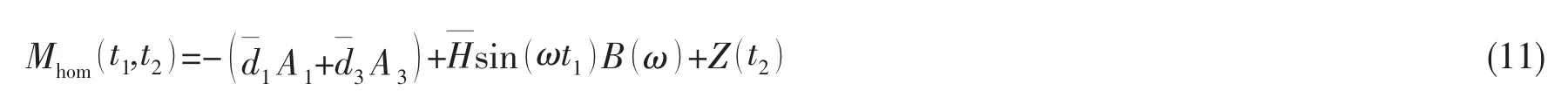
其中，Mhom为同宿轨道的随机Melnikov过程，A1，A3以及B（ω）的表达式如下：所以当y0给定时，A1和A3为常数，B为波浪频率ω的函数。随机Melnikov过程（8）在均方意义下出现零点的条件是：

上式可进一步写为：

随机Melnikov过程具有简单零点，是随机混沌运动的必要条件。本文应用（14）式确定船舶产生混沌运动的参数域，并结合庞加莱截面和响应历程研究甲板上浪船舶的混沌运动。

4 算 例

算例为一艘拖网渔船，该船于1972年制造，1974年在北挪威诺尔辰角西部岛海面附近失事，船舶的主要参数如表1所示[9]。

该拖网渔船具有双层甲板，即捕鱼甲板和主甲板，上层建筑设在船首，在船尾进行捕鱼作业，渔获物直接卸到下层主甲板的加工间进行处理。在船两侧的舷墙上，有24个排水孔，其中右舷13个，左舷11个；在右舷距设计水线1.6m处，有两个0.53m长、0.46m宽的斜道，用来排除加工间产生的杂物，船舶具体结构参见文献[10]。在一定条件下，海水会从排水孔、舷墙顶部以及右舷侧的两个斜道进入甲板并累积[10]。事故发生后，很多机构和学者分析了船舶失事的原因，通过对沉船的实际探测，推测该船的倾覆可能与甲板上浪有关[10]，目前对这一推测还没有从理论上给予足够的证实。下面以该拖网渔船为例，研究甲板上浪时船舶的混沌运动。

将恢复力臂曲线GZm拟合成十三次多项式，代入方程（4），有：

表1 船舶主要参数Tab.1 Principal particulars of the vessel

其中，ki（i=1,3,…,13）分别为线性和非线性恢复力矩系数。根据实验[9]，对于一定量的甲板上浪，与方程（15）对应的船舶参数为：k1=-0.331 1,k3=2.644 6,k5=-6.5698,k7=8.242 1,k9=-5.339 4,k11=1.708 1,k13=-0.214 3,d1=0.056,d3=0.165 9,β0=0.8，参数 E、ω和D依据不同的海况而定。

当周期波浪频率ω=0.5rad/s时，用（14）式计算不同白噪声强度D时船舶发生混沌运动的阻尼系数d1与波浪幅值E间的临界关系，结果如图1所示。

图1 船舶混沌运动的参数区域（ω=0.5rad/s）Fig.1 The parameter domain for onset of chaotic motion of ship(ω=0.5rad/s)

图1中横坐标为波浪幅值E，纵坐标为线性阻尼系数d1，图中曲线为混沌域和非混沌域的分界线，不同的线型表示不同的白噪声强度。由图1可以看出，对于确定的波浪幅值E，增加船舶阻尼将抑制混沌运动的发生；增加白噪声强度，将使非混沌参数域减小、混沌参数域增大；增加波浪幅值，船舶不发生混沌运动的临界阻尼值将随之增大。

以下计算船舶横摇响应的庞加莱截面和时间历程。庞加莱截面的构造方法如下：选定n个不同的初始条件，对每一个初始条件用四阶Runge-Kutta法数值求解方程（15），每经过一个波浪周期取一个相点，计算200个周期，选后50个周期的相点构造庞加莱截面。

根据图1划分的参数区域，在混沌参数域中取两组参数（d1=0.056,D=0,E=0.06,ω=0.5rad/s）和（d1=0.056,D=0.000 5,E=0.06,ω=0.5rad/s），在非混沌参数域中取两组参数（d1=0.1,D=0,E=0.06,ω=0.5rad/s）和（d1=0.12,D=0.000 5,E=0.06,ω=0.5rad/s），分别对一百个初始点和一个初始点计算船舶的横摇响应，构造庞加莱截面，结果如图2～5所示。

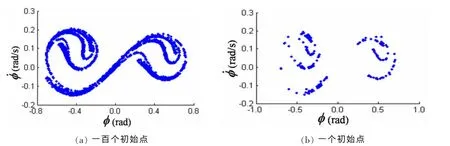
图2 庞加莱截面（d1=0.056,D=0,E=0.06,ω=0.5rad/s）Fig.2 Poincare’ maps(d1=0.056,D=0,E=0.06,ω=0.5rad/s)

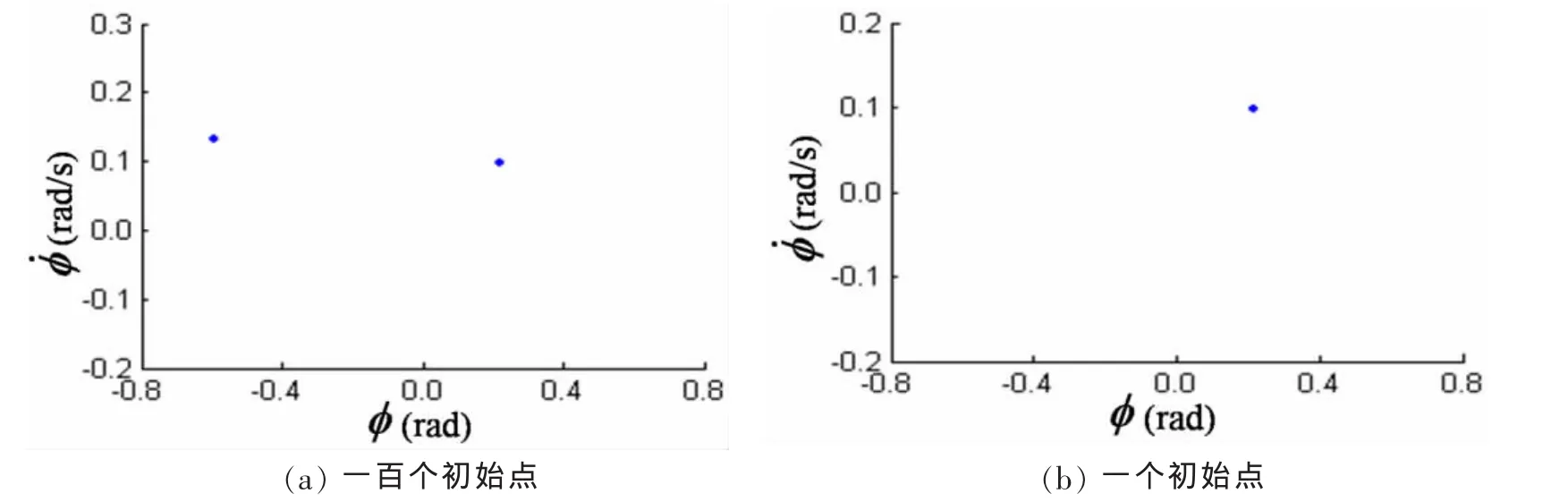
图3 庞加莱截面（d1=0.1,D=0,E=0.06,ω=0.5rad/s）Fig.3 Poincare’ maps(d1=0.1,D=0,E=0.06,ω=0.5rad/s)

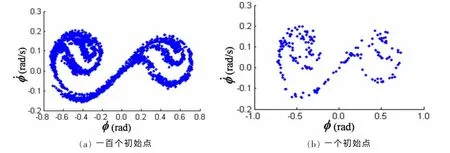
图4 庞加莱截面（d1=0.056,D=0.000 5,E=0.06,ω=0.5rad/s）Fig.4 Poincare’ maps(d1=0.056,D=0.000 5,E=0.06,ω=0.5rad/s)

图5 庞加莱截面（d1=0.12,D=0.000 5,E=0.06,ω=0.5rad/s）Fig.5 Poincare’ maps(d1=0.12,D=0.000 5,E=0.06,ω=0.5rad/s)

由图2和图3可以看出，对于白噪声强度D等于零的情况，当阻尼系数d1=0.056时船舶发生混沌横摇运动，如图2所示；当阻尼系数d1增大到0.1时，船舶横摇为规则的周期运动，如图3所示。由图4和图5可以看出，对于白噪声强度D大于零的情况，当阻尼系数d1=0.056时船舶发生随机混沌运动，如图4所示；当阻尼系数d1增大到0.12时，船舶运动为随机横摇运动，如图5所示。因此，增大横摇阻尼抑制了船舶混沌运动的发生。

图2～5还表明，甲板上浪时船舶横摇响应的庞加莱截面上有两个吸引域，船舶横摇过程有两个横摇中心，分别位于左舷侧和右舷侧。在非混沌参数域，对于任意一组确定的初始条件，船舶围绕其中的一个横摇中心运动，如图3（b）和图5（b）所示；在混沌参数域，响应过程中发生由一个横摇中心到另一个横摇中心的随机跳跃，如图2（b）和图4（b）所示。

用响应的时间历程进一步验证以上结论。对上面的四组参数，计算船舶横摇响应的时间历程，结果如图6和图7所示。

图6 船舶横摇响应历程（D=0,E=0.06,ω=0.5rad/s）Fig.6 Roll response history of ship(D=0,E=0.06,ω=0.5rad/s)

图7 船舶横摇响应历程（D=0.000 5,E=0.06,ω=0.5rad/s）Fig.7 Roll response history of ship(D=0.000 5,E=0.06,ω=0.5rad/s)

图6和图7中的横摇响应历程表明，在非混沌参数域，船舶围绕某一个横摇中心作小幅度横摇，如图6（a）和图7（a）所示；在混沌参数域，响应过程中船舶将随机地由一个横摇中心跳跃到另一个横摇中心，如图 6（b）和图 7（b）所示。

在混沌参数域中另取两组参数，计算船舶横摇响应的庞加莱截面，结果如图8和图9所示。

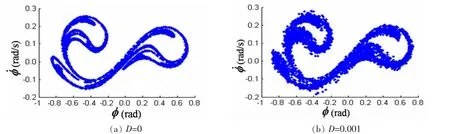
图8 庞加莱截面（d1=0.056,E=0.1,ω=0.5rad/s）Fig.8 Poincare’ maps(d1=0.056,E=0.1,ω=0.5rad/s)

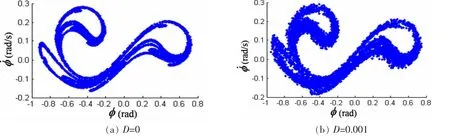
图9 庞加莱截面（d1=0.056,E=0.12,ω=0.5rad/s）Fig.9 Poincare’ maps(d1=0.056,E=0.12,ω=0.5rad/s)

图8和图9表明，在混沌参数域中随机噪声使混沌吸引域的面积有所扩散。

5 结 语

考虑甲板上浪对船舶静稳性的影响，应用随机Melnikov方法和庞加莱截面研究随机横浪中甲板上浪时船舶的混沌运动。由随机Melnikov过程结合均方准则确定产生混沌运动时船舶的阻尼系数与波浪参数间的临界关系，计算不同参数域中船舶横摇响应的庞加莱截面和时间历程。结果表明，增加船舶阻尼将抑制混沌运动的发生；甲板上浪时船舶横摇响应的庞加莱截面上有两个吸引域，船舶运动过程有两个横摇中心；在非混沌参数域，船舶只围绕其中的一个横摇中心运动；在混沌参数域，响应过程中发生由一个横摇中心到另一个横摇中心的随机跳跃。

[1]Dillingham J T,Falzarano J M.A numerical method for three-dimensional sloshing[C]//SNAME Spring Meeting Technical and Research Symposium(STAR).Portland,Oregon:1986:75-85.

[2]黄祥鹿,顾谢忡.船舶甲板上浪横摇的时域模拟[J].中国造船,1993,26(3):27-36.

[3]Belenky V L,Liut D,et al.Nonlinear ship roll simulation with water-on-deck[C]//Proceedings of the Stability Workshop.New York,2002.

[4]Laranjinha M,Falzarano J M,et al.Analysis of the dynamical behavior of an offshore supply vessel with water on deck[C]//Proceedings of the 21st International Conference on Offshore Mechanics and Arctic Engineering(OMAE).Oslo,Norway,2002.

[5]Yim S C S,Lin H.Unified analysis of complex nonlinear motions via densities[J].Nonlinear Dynamics,2001,24:103-127.

[6]Nakhata Tongchate.Stability analysis of nonlinear coupled barge motions[D].Salem:Oregon State University,2003.

[7]McCue L,Troesch A.Probabilistic determination of critical wave height for a multi-degree of freedom capsize model[J].Ocean Engineering,2005,32(13):1608-1622.

[8]朱位秋.非线性随机动力学与控制—Hamilton理论体系框架[M].北京:科学出版社,2003.

[9]Morrall A.The Gaul disaster:A investigation into the loss of a large stern trawler[J].Naval Architect,1981,5:391-440.

[10]Marine accident investigation branch.Report of the re-opened formal investigation into the loss of the FV Gaul,part 2:The subsea surveys from 1997 and the new evidence[R].Published by the Stationery Office,2004.