应用图形处理器实现无功优化并行计算
2011-06-06黄玉龙刘明波
黄玉龙 刘明波
(华南理工大学电力学院 广东省绿色能源技术重点实验室 广州 510640)
1 引言
非线性原对偶内点法具有良好的收敛性和鲁棒性[1-2],为大型电力系统无功优化的快速求解提供了可能。然而,随着现代电网规模的迅速扩大,传统在CPU上实现的无功优化还无法满足在线计算和实时控制的需求。为此,文献[3]提出一种粗粒度的多机并行计算方法求解动态无功优化问题,4机并行计算加速比最高只可以达到1.81。文献[4-5]建立多分区无功优化并行计算模型加速计算,118节点系统分3区并行计算加速比只有1.89[4],而且存在1%左右的误差。
近年来,图形处理器(Graphic Processing Unit,GPU)不断演变为高度并行、多线程多核处理单元,具有很高的处理速度和存储带宽。GPU越来越适用于图形处理外的通用并行计算[6-8],如代数运算[9]、最优化计算[10]、电力系统暂态稳定仿真[11]、电网可视化[12]和医疗成像[13]等。文献[9]基于GPU求解线性方程组,获得一定的加速效果,但还只能实现方程维数低于4096的单精度浮点运算。
为了进一步提高大电网无功优化计算的速度,本文利用NVIDIA 公司GeForce GTX 285 GPU和台式计算(3.0GHz Intel双核CPU,2.0GB内存)构建并行计算环境,GPU和CPU之间接口采用PCIe 2.0x16总线,带宽为8GB/s。通过两者的协同配合来并行实现内嵌离散惩罚的非线性原对偶内点算法。将计算密集部分—线性修正方程的求解在图形处理器上实现,其余部分在CPU上执行。这样可以充分利用GPU的高速浮点运算和高带宽,极大地提高了整体计算速度,可以适应大电网的计算需要。
2 内嵌离散惩罚的非线性原对偶内点法
无功优化在数学上表现为典型的连续和离散变量混合的非线性优化问题[1-2],其模型可描述为
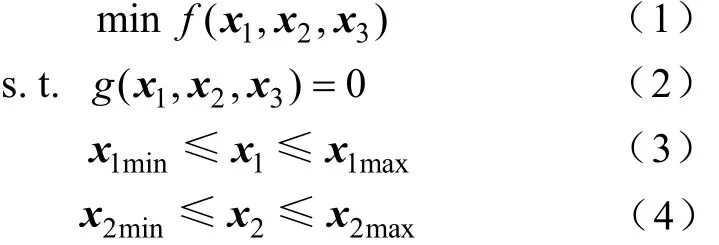
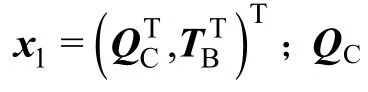
引入松弛变量,将不等式约束式(3)和式(4)转变成等式约束:
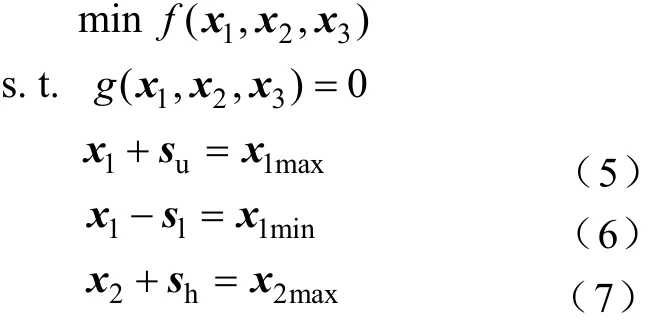

式中,su,sl,sh,sw为由松弛变量组成的列向量,
引入对数壁垒函数消去松弛变量的非负性约束,对等式约束引入拉格朗日乘子,并引入正曲率二次罚函数来处理QC和ΤB这类离散变量[1-2],从而形成如下的增广拉格朗日函数:
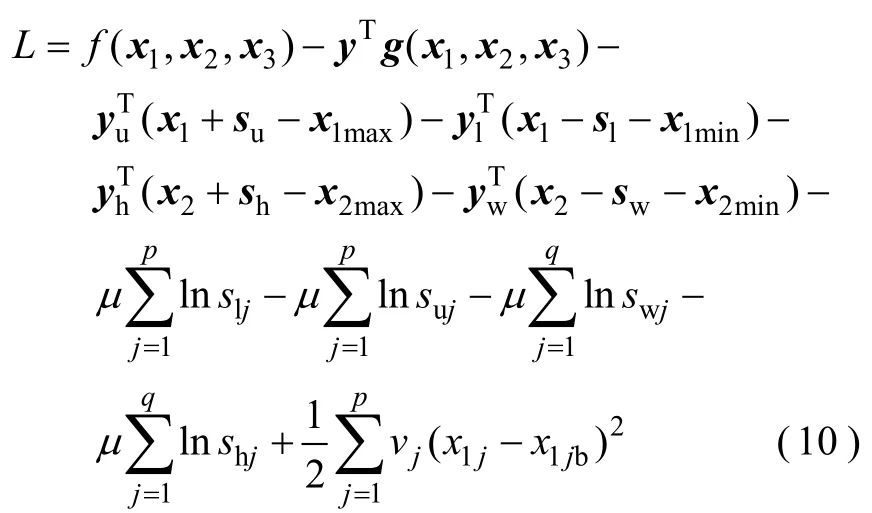
式中,y,yu,yl,yh,yw为拉格朗日乘子向量,,且yu,yh≤0,yl,yw≥0;μ为壁垒参数,且μ≥0;vj为离散变量x1j的罚因子,x1jb为其邻域中心。
根据Karush-Kuhn-Tucker最优性条件可得满足最优性必要条件的非线性方程组,然后线性化得到如下的简化修正方程[1-2]:
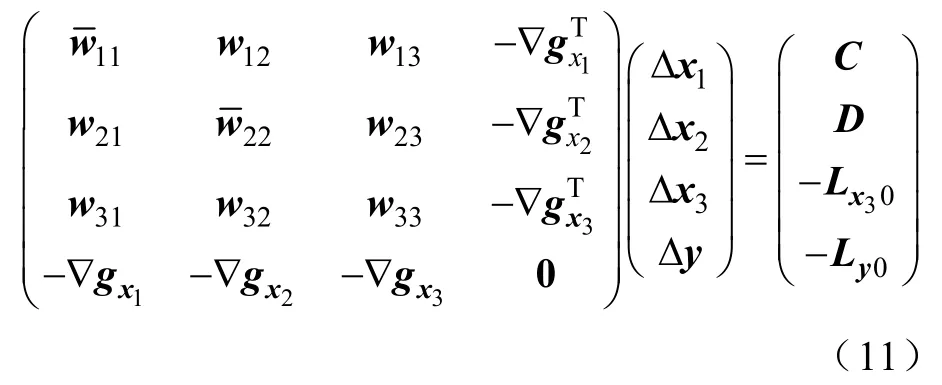
式中,系数矩阵中各元素表达式见式(12)~式(15);Yu,Yl,Yh,Yw,Su,Sl,Sh,Sw分别为以yu,yl,yh,yw,su,sl,sh,sw的分量为对角元素的对角阵。
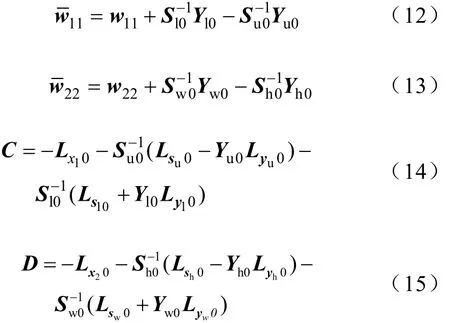
当k=j=1时
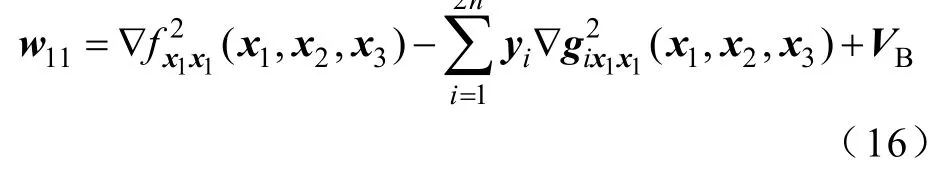
当k≠1且j≠1时
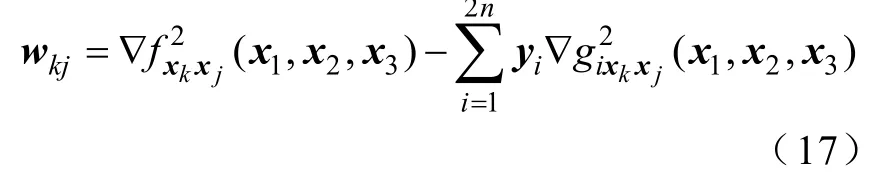
且
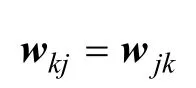
修正方程(简写为AX=B,A是N×N矩阵,X和B是N维列向量,N=3n+p+q)维数N随系统规模迅速增大。例如,某省级1133节点系统N为4960,某区域2212节点系统N为9637。在CPU上反复求解如此高维数的修正方程耗费大量计算时间。经计算表明,在CPU上修正方程的求解时间占全部优化计算时间的96%以上。由于修正方程求解比较适合于并行计算(计算密集、高度并行),所以本文将该部分在GPU上执行,其余部分在CPU上执行。又由于修正方程系数矩阵在迭代过程中是不断变化的,所以对修正方程的求解不采用LU分解法,而采用高斯消去法。计算机中采用单精度浮点数比采用双精度浮点数舍入误差大,而列主元高斯消去法能够减少这种误差的影响,可提高计算精度,保证其数值稳定性。故此,本文采用列主元高斯消去法求解修正方程,并且采用单精度和双精度浮点数运算加以对照。
3 GPU的硬件结构和并行计算原理
3.1 GPU特点和开发工具
NVIDIA公司的GeForce GTX 285 GPU有30个多处理器,时钟1.476GHz;每个多处理器能够同时处理32个warp,每32个并行线程称之为1个warp。显存带宽为158.796GB/s(giga bytes per second)、容量为1GB。同时支持单精度和双精度运算,理论最高运算速度为1062.72Gflops (giga floating-point operations per second)。而目前主流的双核处理器只有不超过25Gflops的浮点运算速度。造成CPU和GPU性能之间的差异主要原因是,GPU是一种针对图形处理的专用处理器,它的特点就是控制部件相对较少,芯片上主要部分都为计算器所占据,片内Cache也很少,因此其专用性决定了它的计算速度是很快的。
GPU是专门为图形运算而设计的,是一种高度并行化的流式处理器,对所有的像素进行并行操作。即,相同或类似的运算会在海量的数据上重复运行,这恰恰符合单指令多数据流的概念。因此,GPU在通用计算方面适合用于诸如科学运算、数据分析、线性代数、流体模拟等需要大量重复的数据集运算和密集的内存存取的应用程序[6]。相比之下,CPU本质上是一个标量计算模型,计算单元偏少,主要针对复杂控制和低延迟,而非高带宽优化。
2006年11月,NVIDIA公司发布了一个在GPU上的开发工具,即统一计算设备构架(Compute Unified Device Architecture,CUDA)。CUDA是一个面向通用计算和图形计算的解决方案,是C语言的一种扩展。CUDA程序构架分为两部分:主机和设备;主机指的是CPU,设备指的是GPU。主程序由CPU来执行,而当遇到数据并行处理部分,CUDA就会将程序编译为GPU能执行的代码,传送到GPU执行。这个并行处理程序在CUDA里称为“核”程序。当调用“核”程序时,m个线程并行地执行相同指令,加速比达到m。GPU作为运行 C 语言程序主机的协同处理器,“核”在 GPU 上执行,而程序的其他部分在CPU上执行[14-15],即串行代码在CPU上执行,并行代码在GPU上执行。
3.2 GPU的硬件结构
CPU的硬件结构如图1所示。通过CUDA编译时,GPU可以被视为能执行高数量并行线程的计算设备,运行在主机上的并行数据和高密度计算应用程序部分被卸载到这个设备上。设备被看作一组带有片上共享内存的多处理器,每个多处理器有8个标量处理器、一个多线程指令单元和片上共享内存。每个多处理器使用四种片上内存:寄存器、共享内存、只读常量缓存和只读纹理缓存。另外,每个多处理器还有2个特殊函数处理单元用来计算诸如正弦和余弦函数等特殊函数。主机和设备使用它们各自的DRAM:主机内存和设备内存(见图1),并能相互复制数据。“核”程序只能在设备内存上执行。
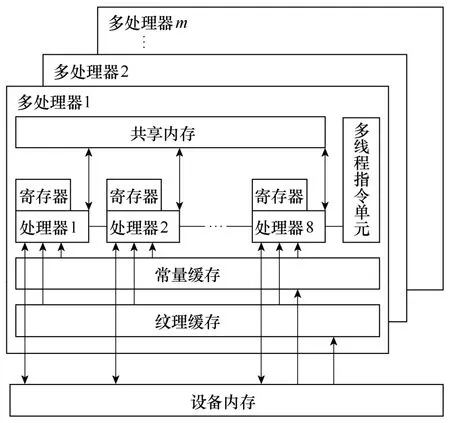
图1 GPU硬件结构Fig.1 GPU hardware structure
每个多处理器使用单指令多线程架构(Single-Instruction Multiple-Thread,SIMT)[16]:在任何时钟周期内,每个线程被映射到一个标量处理器上,各自独立地按照其指令地址和寄存器状态执行;SIMT按照每32个并行线程为单位(称为1个warp)来创建和组织执行各个线程。同一个warp中的线程按照相同的程序地址启动执行,之后却可以按照不同的分支路径独立执行。这样,当同一warp内的32个线程执行相同的路径时,效率最高;而当这32个线程遇到流控制指令(if,switch,do,for,while)发生分支而执行不同路径时,不同路径线程将被序列化地执行,效率下降。
3.3 线程调用层次结构
CUDA将计算分层,如图2所示。计算的最小单位是线程;线程块是指线程的批处理,是一个多处理器上运行的最小单位。各线程块包含相同数量的线程,它通过快速的共享内存有效地分享数据,并且可以在指定的内存访问中同步线程地执行。
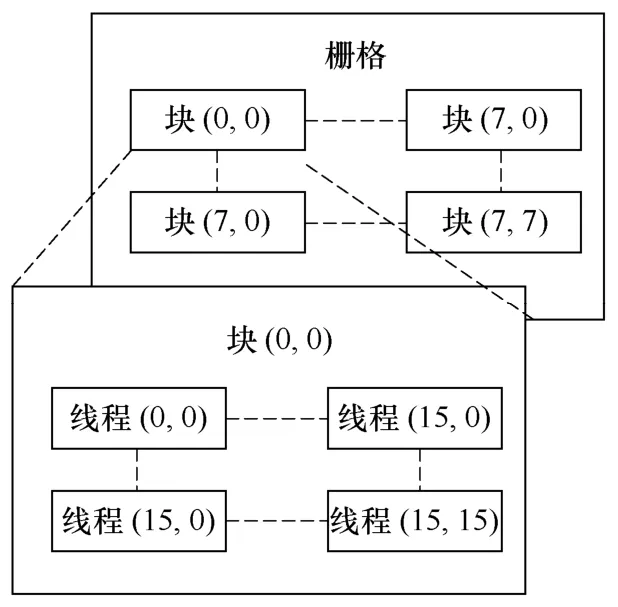
图2 线程块栅格结构Fig.2 Grid of thread blocks
执行同一“核”程序的块可以合成一批线程块的栅格,因此通过一个“核”程序发送请求的线程总数是每个块内的线程数与块数量的乘积。栅格是主机调用GPU的最小单位。通常调用一个“核”程序(名为kernel)的形式如下:
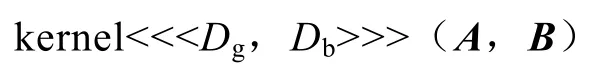
其中,Dg为指定栅格的维数和大小;Db为指定每个块的维数和大小;A,B是“核”程序计算用参数。图2中Dg为(8,8)二维栅格,共有64个块;Db为(16,16)二维块,每块共有256个线程。这样,“核”程序发送请求的线程总数为64×256个线程。
栅格中线程块的数目应当大于多处理器的数量,使得每个多处理器都处于工作状态。进而,为了使得在线程同步时处理器不会处于等待状态,每个多处理器需要数倍数量的活动线程块。同时,为了适应设备升级的需要,应当为“核”程序配置数百个或数千个线程块[17]。
块内线程数量应当是warp尺寸(即32)的倍数,避免在线程不足的warp上浪费计算能力,也有利于实现访问内存联合,最好采用128~256[17]。
3.4 内存体系结构
CUDA 线程可在执行过程中访问多个存储器空间的数据,如图3所示。每个线程都有一个私有的本地内存。每个线程块都有一个共享内存,该内存对于块内的所有线程都是可见的,并且与块具有相同的生命周期。所有块内的线程都可访问相同的全局内存。此外只读常量缓存空间和只读纹理缓存空间可由所有线程访问。
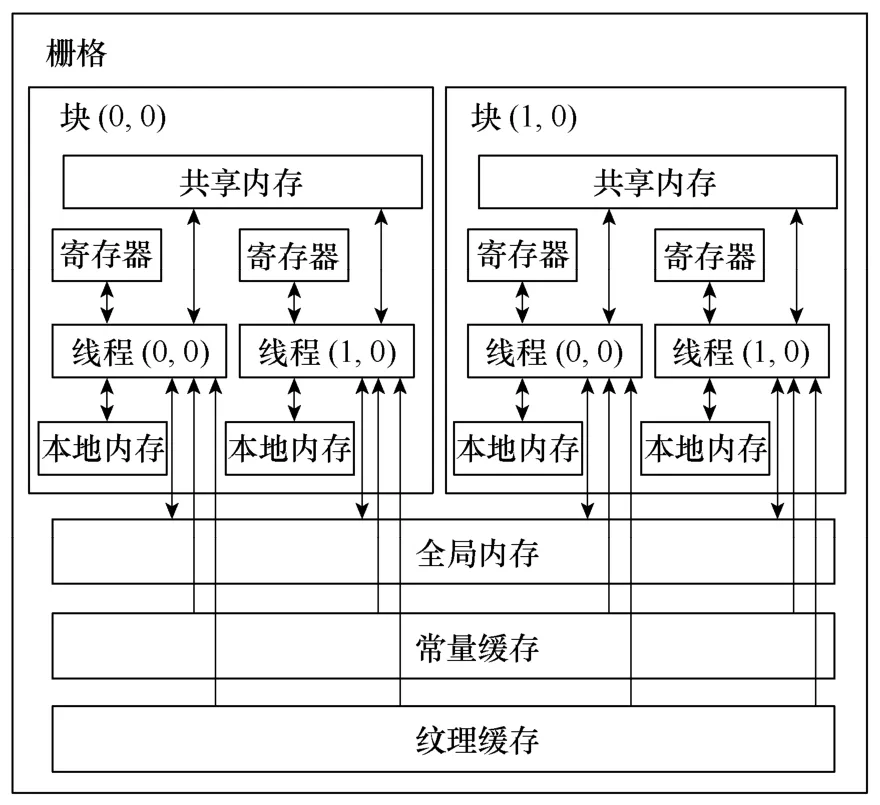
图3 内存体系结构Fig.3 Memory hierarchy
每个处理器有一组本地寄存器。当存在从寄存器读取数据依赖于对寄存器写的结果时,或者当半个warp的线程访问寄存器出现冲突时,访问寄存器需要延时[14]。除此之外,读写寄存器不花费额外时间。
由于共享内存是片上的,所以它比本地和全局内存空间更快;同时为了提高内存带宽,共享内存空间被划分为大小相等的内存模块,称为bank[14,17]。当访问共享内存的w个地址分别位于w个不同的bank时可以同时访问,带宽提高到原来的w倍;而当内存请求的多个地址位于同一个bank中,就存在bank冲突,访问必须被序列化,带宽降低。事实上,对于一个warp的前半或者后半16个线程访问共享内存不存在bank冲突时,访问共享内存和访问寄存器一样快。
本地和全局内存作为设备内存的读写区域没有被缓存,相对片上内存而言,具有较大的时间延迟、较低的带宽。经测试,本机主存到设备全局内存的带宽只有1.304GB/s、反向传输带宽1.327GB/s、设备到设备全局内存之间的传输带宽只有0.3MB/s,远远低于其显存带宽,制约其性能的有效发挥。算法设计中应当尽量减少通过本地和全局内存进行数据传输。另外,为了获得较高的带宽,访问全局内存要遵循特殊的访问模式。半个warp的16个线程访问地址连续的若干全局内存空间,称为联合的全局内存访问模式。全局内存访问联合时,一次或两次读、写操作就可以完成访问;反之,访问被序列化,有效带宽降低[17]。算法设计中应当首先保证全局内存访问被联合。
由于纹理作为设备内存的读区域被缓存了,当纹理缓存没有被错过时,一个纹理操作只消耗纹理缓存的一个读操作,否则,消耗一个从设备内存的读操作。所以,通过纹理缓存读取设备内存相对于从全局或常量内存读取设备内存有更高的带宽[14-17]。另外,纹理拾取可以避免从全局内存未联合存取[17],增加有效带宽。
4 线性方程组单精度和双精度算法
4.1 三种计算方案
本文在GPU上使用三种方案对线性方程组(AX=B)求解。方案一采用纹理缓存空间存取矩阵、向量,只支持单精度浮点数据格式;方案二、三采用global内存空间存取矩阵、向量,方案二用单精度浮点数据格式,而方案三用双精度浮点数据格式。
各方案采用填充技术存放矩阵A,在每行最后一个元素后面填充一些存储空间使得每行有256的倍数个元素,从而半个warp的16个线程可以方便地访问地址连续的若干全局内存空间,使得global存储访问区域被联合,提高访问效率。图4表示212×212维线性方程组第k+1次消去运算的情形。图4中,A、B各元素分别用a、b加下标表示,* 符号表示内存填充区。本机最多能够填充32 768个单精度浮点数、16 384个双精度浮点数,从而本算法可以求解维数低于32 768单精度、维数低于163 84双精度线性方程组。
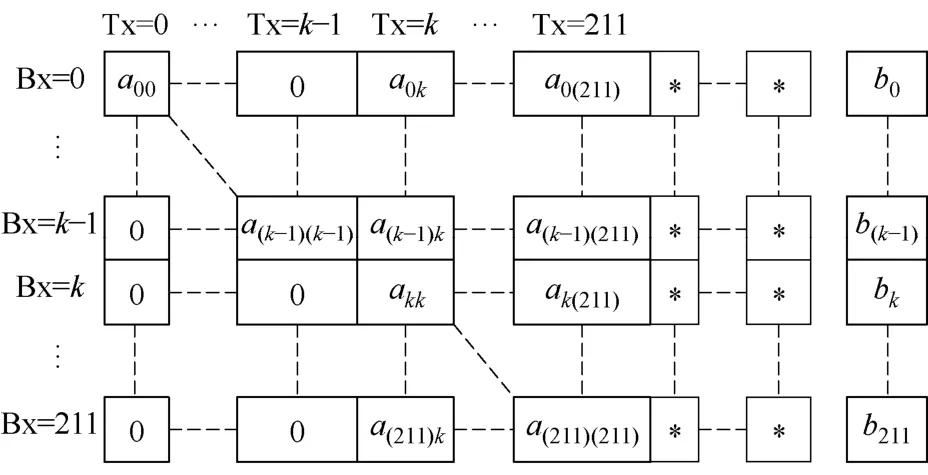
图4 解212×212线性方程时第k+1次消去运算Fig.4 The k+1th elimination for solving 212×212 linear equation
各方案用一个线程块(图4中索引号为Bx)负责矩阵一行元素的计算,使线程块数量最大化,提高处理器的计算效率。块内线程数量采用256,在维数大于256维的线性方程组中用循环访问矩阵A。每个线程(图4中索引号为Tx)对应计算矩阵的一个元素。这样,求解212×212维线性方程组“核”程序线程块总数为212,每个块内线程数为256。
“核”程序通过一个名为“纹理撷取”的设备函数读取纹理内存。“纹理撷取”函数的第一个参数指定一个叫“纹理参照”的对象,该函数通过纹理坐标来撷取绑定到“纹理参照”的内存。“纹理参照”有一些属性,其一是纹理尺寸,它定义是否可以通过一元纹理坐标指定纹理按一维数组寻址,或者通过二元纹理坐标指定纹理按二维数组寻址,亦或通过三元纹理坐标指定纹理按三维数组寻址;另外,定义输入输出数据类型和数据读取模式等。在方案一中,系数矩阵A用单元素二元纹理坐标寻址,向量B用单元素一元纹理坐标寻址。由于GPU对二元纹理坐标寻址进行了优化,这样就可以充分利用显存的高带宽[17],同时利用二元纹理坐标下的纹理元素和矩阵元素间的一一对应关系,便于检索。
由于在同一个“核”程序中,当对绑定到纹理的global内存地址修改后进行纹理撷取,将取出不可预知的数据[17]。这意味着,只有对已经在前面“核”程序或者数据复制中更新过的global内存地址进行纹理撷取才准确。因此在方案一中,采用在global内存中分配两个区域存储矩阵A及其中间结果。交替将计算结果输出到其中一个区域。而其余向量不需要在同一个“核”程序中进行更新后撷取,只用一个区域即可。在方案二和方案三中,因为global内存是可以在同一个“核”程序中读写,所以当采用global存储时,不必使用两个区域,减少数据传递量。
为了利用共享内存和寄存器的快速存取特性,所有“核”程序采用下面的编程模式:
(1)从设备内存加载数据到共享内存或寄存器。
(2)在共享内存和寄存器上处理数据。
(3)与块内的其他线程同步,以便每条线程可以安全地读取由不同线程写入的共享内存的存储单元。
(4)把结果写回到设备内存中。
4.2 计算流程
方案一的算法流程如下:
(1)将A和B中各元素复制到GPU全局内存;
(2)循环fork=0 toN-2:
①将源区域绑定到纹理;
②取出矩阵第k+1列向量,找出其中第k+1到N个元素(即图4中akk到a(211)k)中绝对值最大的元素;
③在源区域进行行交换,对B进行元素交换;
④消去运算,输出到目标区域;
⑤将元素a(k,k)从目标区域输出到源区域;
⑥更换目标区域和源区域;
(3)结束循环;
(4)进行标准化计算,即bk/akk(fork=0 toN-1),将结果输出到主机,结束计算。
方案二、三只用一个global内存区域存取矩阵A,其余的计算流程与方案一相同。
设步骤①中第k+1~N个元素用向量o表示。首先进行第一次比较,将向量o的前半部分和后半部分元素进行一一对应比较,将绝对值较大的元素放入前半部分,后半部分保持不变;然后,将o的前半部分继续分为前半、后半两部分,按上面方法处理;继续这一过程直到寻找出最大值。当向量大小不是2的整数倍时,在后面补入零元素,使其成为2的整数倍。这样对于N维向量只需要进行ceil(log2N)次比较就能找出最大值(ceil表示向上取整),而在CPU上需要进行N-1次比较,极大地提高了计算效率,N越大,效率越高。
步骤④将前代和回代过程合并在一起计算。即第k+1次迭代时,将矩阵A的右下部分和右上部分、向量B前部和后部同时进行消去计算(见图4),共需更新(N-1)×(N-k)个元素。
4.3 计算效率
采用上述三种计算方案获得的加速比(加速比为算法在CPU上执行时间与在GPU上执行时间的比值)如图5所示。加速比随着线性方程组维数的增大而不断增大,达到一定维数时趋于饱和。单精度计算在方程组维数到达6000×6000时饱和;双精度计算在方程组维数到达3000×3000时饱和。方案一最大加速比57.46,方案二最大加速比43.56,方案三最大加速比10.58。可见,方案二相比方案一计算速度下降不少,这是由于 global存储速度明显低于texture缓冲存取速度,方案三计算速度最低,这是由于GPU原本是为图形处理而设计的,其单精度浮点运算速度是最快的。故此,虽然当GPU计算能力达到1.3[18]时,CUDA支持双精度浮点计算,在精度满足要求时最好还是采用单精度浮点运算。
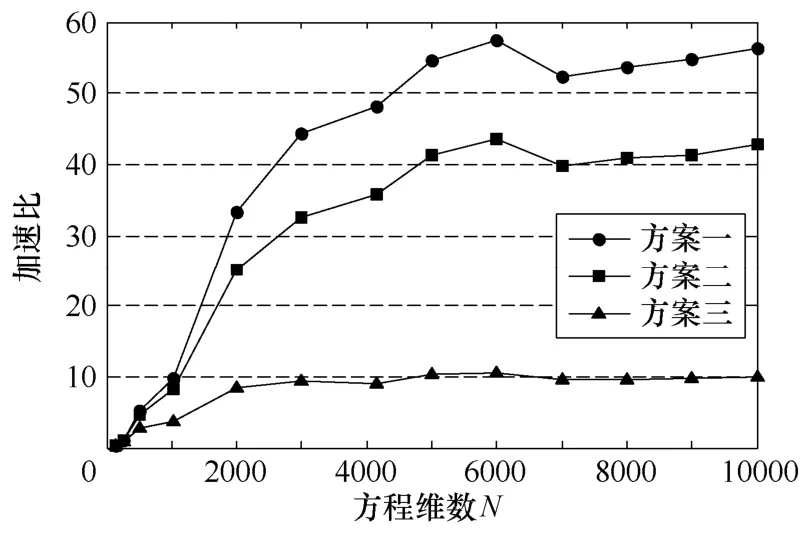
图5 三种方案加速比对照Fig.5 Speedup comparison of three schems
从图6中可以看到,由于当同一warp中的线程发生分流时计算效率下降,在方案一中对一般线性方程组进行计算时,考虑零元素后会使加速比明显下降。
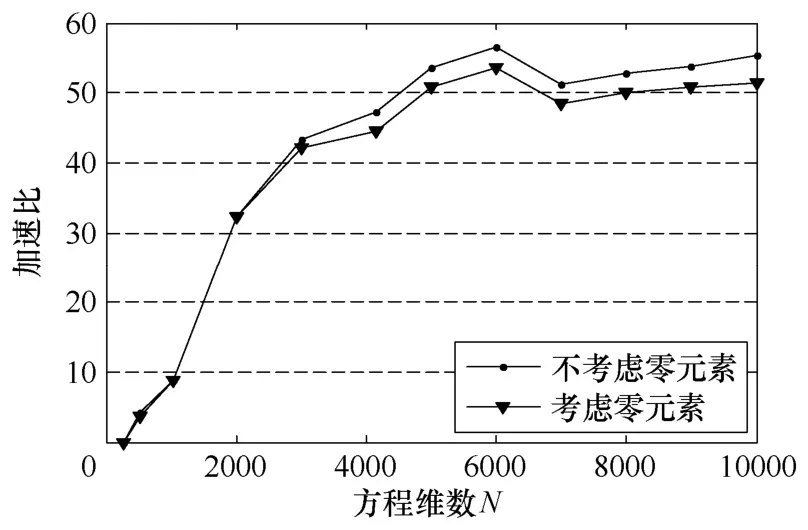
图6 考虑矩阵A零元素后对加速比的影响Fig.6 Effect on speedup after considering zero element in matrix A
分别采用Matlab CPU版本(简称Matlab)、C语言CPU版本(简称CPU版本)和方案一C语言GPU版本(简称GPU版本)求解线性方程组,并在图7中给出了计算时间对比。当方程维数大于256×256时,GPU版本的计算时间大于CPU版本的;当方程维数大于580×580时,GPU版本的计算时间大于Matlab的。虽然Matlab采用相当好的优化计算,GPU版本对高维线性方程组的求解速度还是远远高于Matlab的。图8给出了采用纹理撷取的GPU版本相对于Matlab的加速比,其曲线呈波浪形上升,在方程维数达到7680×7680以上时趋于饱和,最高加速比可达3.79。加速比会出现局部下降现象,这是由于GPU全局内存的存取特性决定的。当一个warp的前半或者后半16个线程存取联合的全局内存时,存取速度是最快的。GTX 285图形处理器的纹理联合区域和全局内存联合区域大小为256B。当方程维数适合联合内存区域大小时,程序获得最好的计算速度,反之,速度下降。
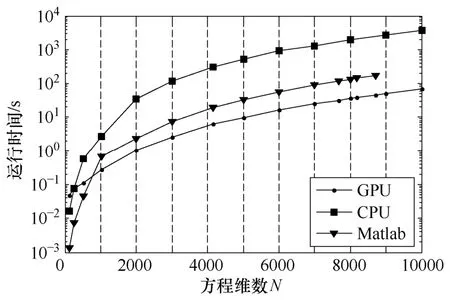
图7 线性方程组计算效率比较Fig.7 Comparison of computational efficiency for solving linear equation
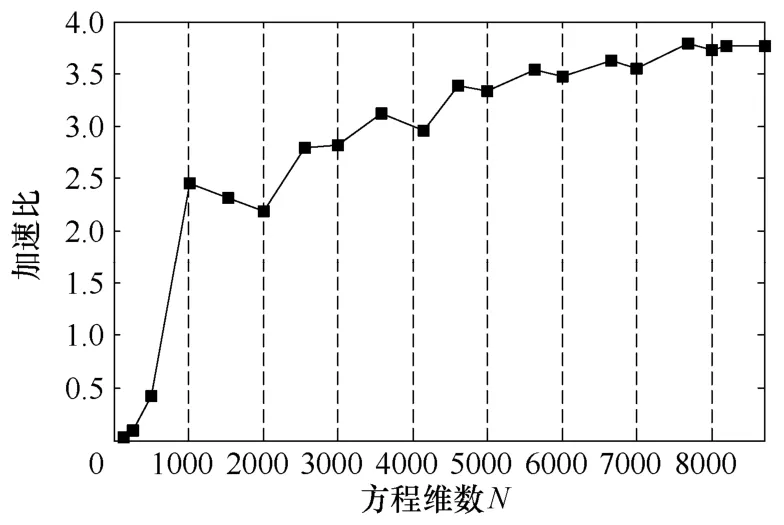
图8 采用纹理撷取的GPU版本相对于Matlab的加速比Fig.8 Speedup of GPU version by texture fetching ralative to Matlab
文献[9]采用高斯消去法和LU分解法基于GPU求解线性方程组,获得一定的加速效果,但只能进行方程维数小于4096的单精度浮点运算。Matlab在本机只能求解维数低于8859的线性方程组,而本文算法则可以求解维数低于32 768单精度、维数低于16 384双精度线性方程组,对大电网计算有较好的适应性。
5 无功优化计算性能比较
分别用上述三种方案进行无功优化计算,以IEEE 118节点和538、1133和2212节点系统为例进行了测试,系统基本数据见表1。
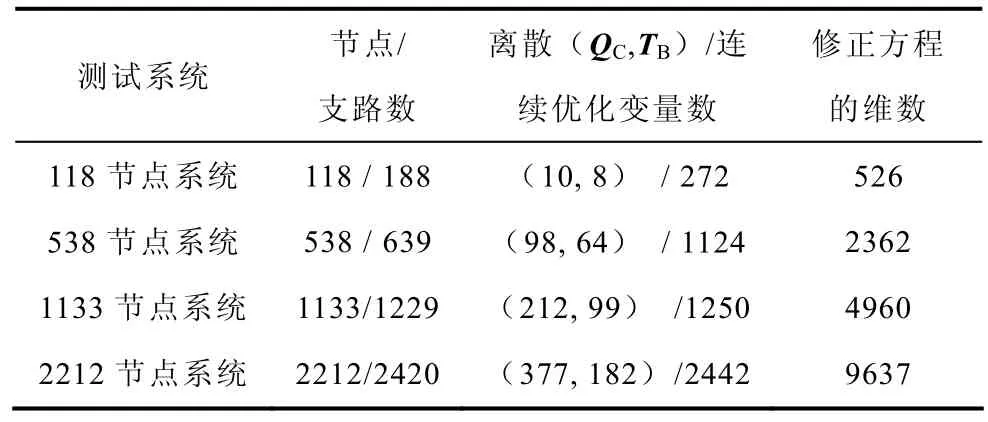
表1 测试系统基本数据Tab.1 Basic dates of test systems
5.1 收敛特性
补偿间隙 ζ 的变化反映了优化过程中满足不等式约束的情况。补偿间隙 ζ 计算公式如下:
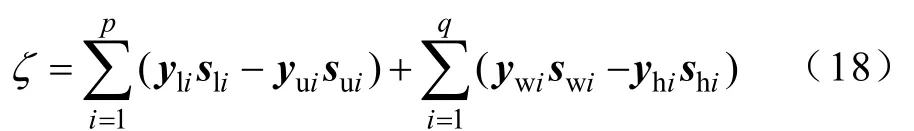
对上式进行误差分析:
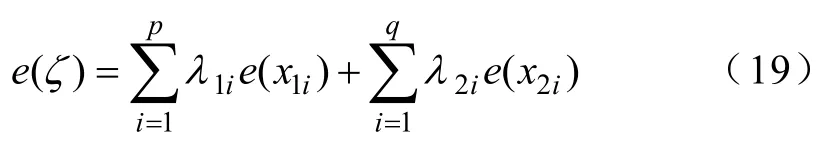
式中,e表示参数的误差;λ1、λ2分别为向量x1、x2各元素的误差系数。忽略各变量间误差和误差系数的不同,进行简化处理:
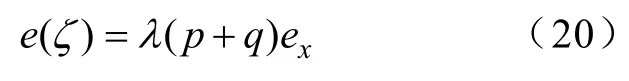
式中,ex、λ为向量x1、x2近似误差和近似误差系数。由式(22)可见补偿间隙误差e(ζ)随系统规模的增大而线性增大。为了消去系统规模对补偿间隙的影响,定义修正补偿间隙ζλ如下:

采用修正补偿间隙ζλ做收敛判据,那么在ζλ<ε1时输出最优解,结束计算。ε1为收敛精度。经过对4个测试系统的计算,采用修正补偿间隙做收敛判据能够较好地适应各种规模电网无功优化计算的需要,使得收敛精度统一。本文收敛精度ε1取2×10-6,最大迭代次数K设为50。图9所示为538和2212节点系统迭代中ζλ变化曲线,单精度和双精度计算都可以很快地收敛,收敛曲线基本一致。
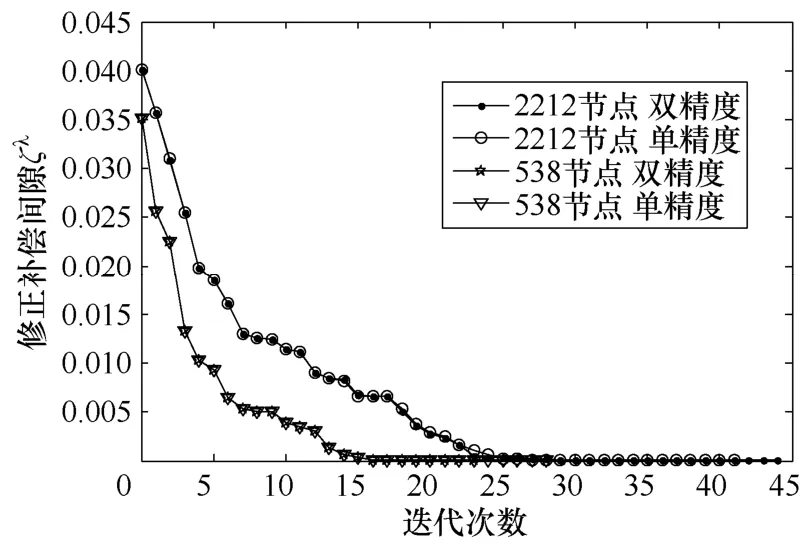
图9 迭代中修正补偿间隙的变化轨迹Fig.9 Trajectories of corrected complementary gap with iterations
5.2 加速比
按照Amdahl定律,将顺序程序并行化后可以获得的理论加速比β[18]
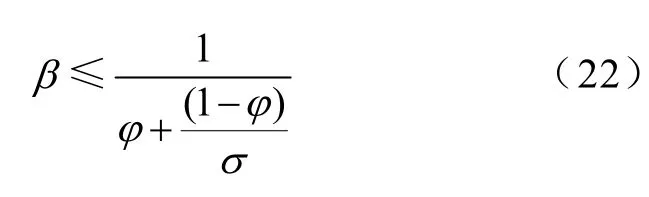
式中,φ是不可并行化程序所占比例;σ是并行处理器数量。考虑到CPU和GPU频率差异的影响,上式应当修改为
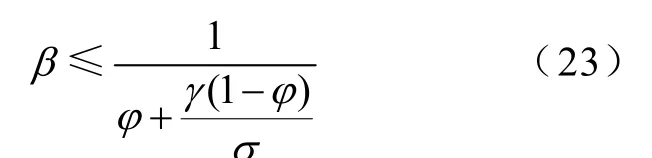
式中,γ为CPU和GPU频率比值。
4个系统的计算结果见表2。由表2可见,采用单精度时计算速度是采用双精度时的4倍左右;最高加速比出现在单精度计算2212节点系统时,高达28.706,用时42min。但是,最高理论加速比仍然是最高加速比的4倍左右,主要原因有两点:第一,GPU设备到设备全局内存之间的传输带宽只有0.3MB/s,远低于显存带宽8GB/s,降低了程序的计算效率;第二,采用GPU编程不能够很好地利用修正方程系数矩阵的高度稀疏性,以单精度为例进行对照见表3。由于CPU计算可以有效地利用修正方程的稀疏性,计算修正方程的加速比为计算一般线性方程加速比的一半。
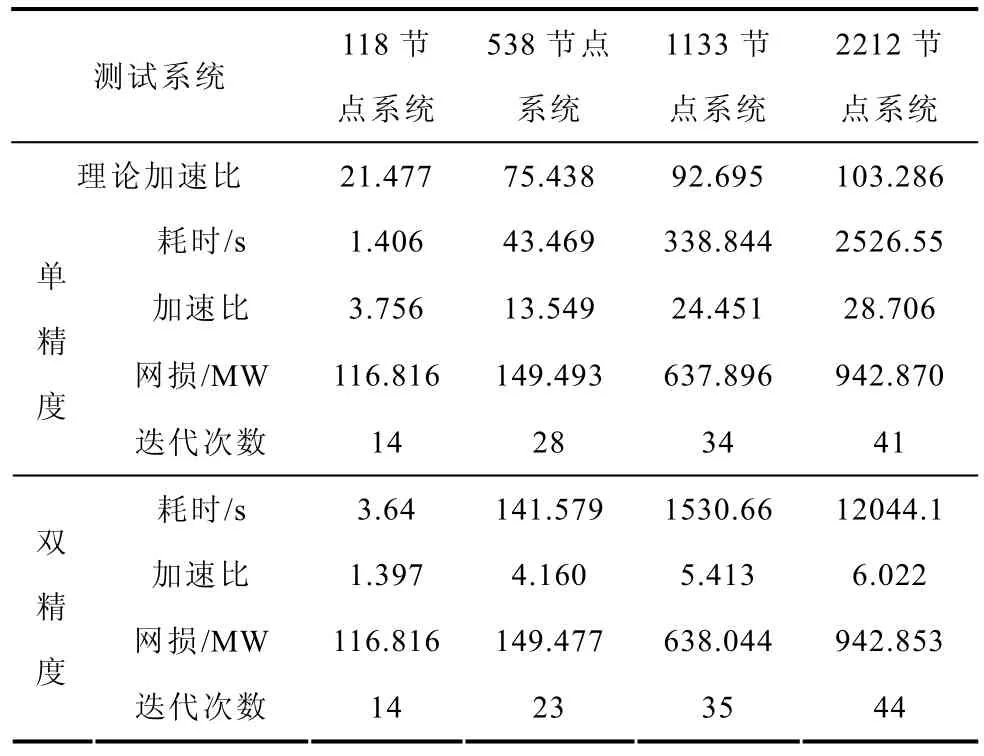
表2 四个系统的无功优化计算结果Tab.2 Results of reactive optimization in four power systems
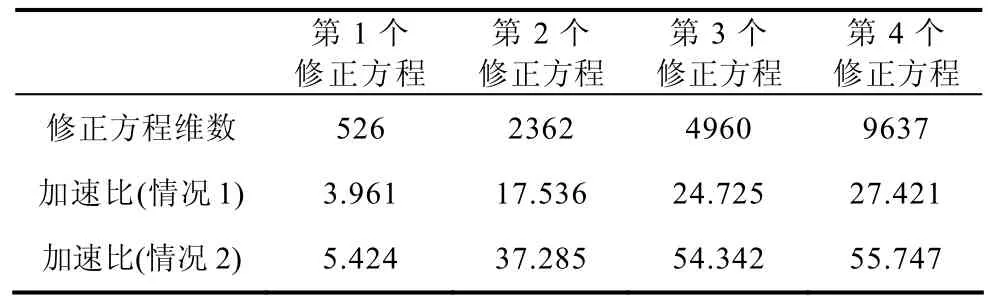
表3 系数矩阵稀疏性对求解修正方程加速比的影响Tab.3 Effect of sparsity of coefficient matrix on speedup in solving the correction equation
6 结论
本文应用GPU来并行实现内嵌离散惩罚的非线性原对偶内点算法,并应用于四个测试系统的无功优化计算,主要有以下优点:
(1)充分利用了GPU的高速浮点运算和高带宽,将线性修正方程的求解在GPU上实现,其余部分在CPU上执行,极大地提高了整体计算速度。相对纯CPU双精度计算,单精度计算加速比达到近30,双精度计算最高加速比超过6,远高于多机并行计算速度。
(2)在GPU上可实现求解维数低于32768单精度、维数低于16384双精度线性方程组,能够适应大电网计算需要。
[1] 程莹,刘明波.含离散控制变量的大规模电力系统无功优化[J].中国电机工程学报,2002,22(5): 54-60.Cheng Ying,Liu Mingbo.Reactive-power optimization of large-scale power systems with discrete control variables[J].Proceedings of the CSEE,2002,22(5):54-60.
[2] Liu M B,Tso S K,Cheng Y.An extended nonlinear primal-dual interior-point algorithm for reactive-power optimization of large-scale power systems with discrete control variables[J].IEEE Transactions on Power Systems,2002,17(4):982-991.
[3] 缪楠林,刘明波,赵维兴.电力系统动态无功优化并行算法及其实现[J].电工技术学报,2009,24(2):150-157.Miao Nanlin,Liu Mingbo,Zhao Weixin.Parallel algorithm of dynamic reactive power optimization and its implementation[J].Transactions of China Electrotechnical Society,2009,24(2): 150-157.
[4] 刘宝英,杨仁刚.采用辅助问题原理的多分区并行无功优化算法[J].中国电机工程学报,2009,29(7):47-51.Liu Baoying,Yang Rengang.Multi-subarea parallel reactive power optimization based on APP[J].Proceedings of the CSEE,2009,29(7): 47-51.
[5] 程新功,厉吉文,曹立霞,等.基于电网分区的多目标分布式并行无功优化研究[J].中国电机工程学报,2003,23(10): 109-113.Cheng Xingong,Li Jiwen,Cao Lixia,et al.Multi-objective distributed parallel reactive power optimization based on subarea division of the power systems[J].Proceedings of the CSEE,2003,23(10):109-113.
[6] 吴恩华.图形处理器用于通用计算的技术、现状及其挑战[J].软件学报,2004,15(10): 1493-1503.Wu Enhua.State of the art and future challenge on general purpose computation by graphics processing unit[J].Journal of Software,2004,15(10):1493-1503.
[7] 吴恩华,柳有权.基于图形处理器(GPU)的通用计算 [J].计算机辅助设计与图形学学报,2004,16(5):601-612.Wu Enhu,Liu Youquan.General purpose computation on GPU[J].Journal of Computer-Aided Design & Computer Graphics,2004,16(5): 601-612.
[8] John D Owens,Mike Houston,et al.GPU computing[J].Proceedings of the IEEE,2008,96(5):879-899.
[9] Nico Galoppo,Naga K Govindaraju.LU-GPU:efficient algorithms for solving dense linear systems on graphics hardware[C].Proceedings of the ACM/IEEE SC 2005 Conference,2005: 3-15.
[10] 姜珊珊.基于GPU的修正单纯形方法的实现[D].吉林: 吉林大学,2008.
[11] Vahid Jalili Marandi,Venkata Dinavahi.Large-scale transient stability simulation on graphics processing units[C].Power & Energy Society General Meeting,Calgary,2009: 1-6.
[12] Joseph Euzebe Tate,Thomas J Overbye.Contouring for power systems using graphical processing units[C].Proceedings of the 41st Annual Hawaii International Conference on System Sciences,Waikoloa,HI,USA,2008: 1351-1360.
[13] Pan Yongsheng,Ross Whitaker.Feasibility of GPU-assisted iterative image reconstruction for mobile C-arm CT[C].Proceedings of the SPIE-The International Society for Optical Engineering,Lake Buena Vista,FL,USA ,2009: 72585J (9 pp.).
[14] Nvidia.CUDA Programming Guide (Version 2.3)[M].July 2009.
[15] Ziyad S Hakura,Anoop Gupta.The design and analysis of a cache architecture for texture mapping[C].Proceedings of the 24th Annual International Symposium on Computer Architecture,1997: 108-120.
[16] Nvidia.CUDA Programming Guide (Version 2.1)[M].Dec 2008.
[17] Nvidia.CUDA C Programming Best Practices Guide[M].July 2009.
[18] Blythe D.Rise of the graphics processor[J].Proceedings of the IEEE,2008,96(5): 761-778.
