三相电压调整模块中“EΠ”形耦合电感的建模与设计
2011-06-06杨玉岗李洪珠冯本成
杨玉岗 李洪珠 冯本成
(辽宁工程技术大学电气与控制工程学院 葫芦岛 125105)
1 引言
随着新一代微处理器的发展,要求为微处理器提供电能的电压调整模块(VRM)具有更大的电流(超过100A)、更低的电压(小于1.2V)、更高的效率、更大的负载阶跃以及小于100mV的输出电压容差[1-2]。为实现这一目标,当前大多数VRM采用多相交错并联技术,把VRM传递的功率平均分布在各相上,并可以减小输入电容和输出电容的电流纹波,然而,在电感值和开关频率给定的情况下,多相交错并联VRM中流过电感器和开关器件的纹波电流与单相VRM相同[3]。虽然通过减小电感值可以提高VRM的暂态响应速度,但是增加了输出纹波电流,降低了VRM的效率[4]。为了解决这一问题,人们在采用交错并联技术的同时,研究了集成磁技术,即将VRM中的各相分立电感集成为反向耦合电感[3-12],多相交错并联VRM采用这种反相耦合的电感,可以在保持稳态电流纹波不增加的情况下提高暂态响应速度,或者在保持暂态响应速度不降低的情况下减小稳态电流纹波[3],从而提高效率,与此同时可以减少电感器和输出电容器的总体积。为此,文献[3-12]给出了多种磁集成耦合电感结构,但文献[3,5-11]的结构只能用于两相耦合,不能用于更多相的耦合,文献[4,12]的结构虽然可以用于多于两相的耦合,但绕组路径较长,应用于低压大电流VRM时电阻损耗较大。
为了克服现有耦合电感器结构的这些不足,本文在文献[8]的基础上,提出了一种耦合结构比较简单且绕组路径长度较小的三相平面磁集成耦合电感结构,本文称其为“EΠ”形铁心结构,这是因为它包括两片铁心,其中一片铁心的形状像“E”,另一片铁心的形状像“Π”。通过分析耦合电感的磁通分布,建立了磁路模型及包括气隙边缘磁阻和绕组外面空气磁阻的改进磁路模型,采用空间切割的方法得出空气磁阻的计算公式,从而得出自感、漏感和互感的计算公式,给出耦合电感器的设计方法,通过三维电磁场有限元仿真和实验验证了所提“EΠ”形耦合电感结构的有效性及其磁路模型和设计方法的正确性。
2 三相EΠ形耦合电感器的结构
三相交错并联电感耦合VRM的拓扑结构如图1所示。图中,v1、v2、v3分别为加在三相电感绕组上的电压,i1、i2、i3分别为流过三相电感绕组的电流,Vin和Vo分别为VRM的输入和输出电压。由于是反向耦合,所以M<0。
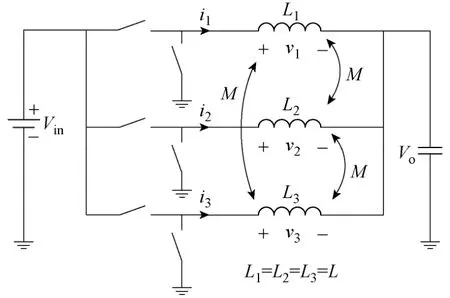
图1 三相交错并联磁耦合VRM的拓扑结构Fig.1.Topology of 3-phase interleaving VRM with coupled inductors
假设三相耦合电感是对称的,则其电压方程为
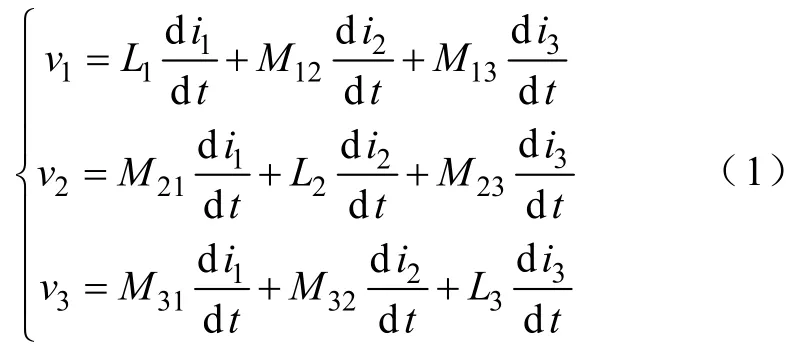
式中,L1、L2、L3为三相耦合电感器的自感,L1=L2=L3=L,Mij(i=1,2,3;j=1,2,3;i≠j)为各相绕组之间的互感,M12=M21,M13=M31,M23=M32。设耦合系数为k,则k=Mij/L,由于是反相耦合,所以-0.5≤k≤0。
图1中三相耦合电感的电路模型如图2所示[13]。图中Trj(j=1,2,3)为各相绕组之间的全耦合变压器模型,Lkj(j=1,2,3)为各相绕组的漏感,并有
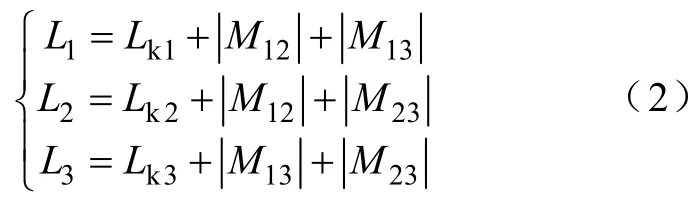
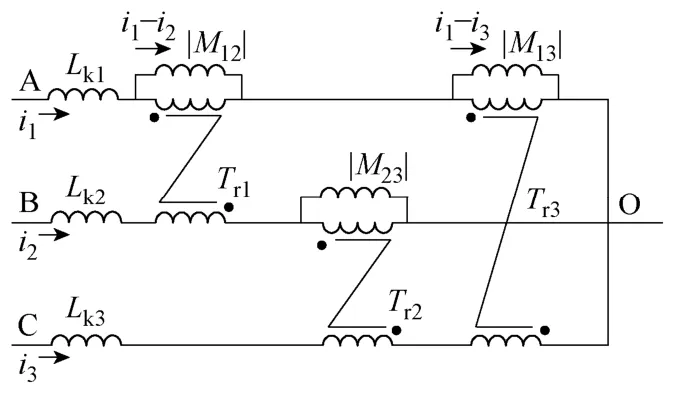
图2 三相耦合电感器的电路模型Fig.2 Circuit model of 3-phase coupled inductors
为了实现图1中的耦合电感,本文提出如图3所示的三相耦合电感器结构,它包括两片铁心,其中一片的形状像“E”,另一片像“Π”,故称为平面磁耦合“EΠ”形结构。图中,“1”表示“E”形铁心;“2”表示“Π”形铁心;“3”表示“E”形铁心的磁柱;“4”表示“Π”形铁心的磁柱;“5”表示绕组。“E”形铁心的三个磁柱用于绕制三相耦合电感的绕组,“Π”形铁心的两个磁柱用于调节耦合系数k。
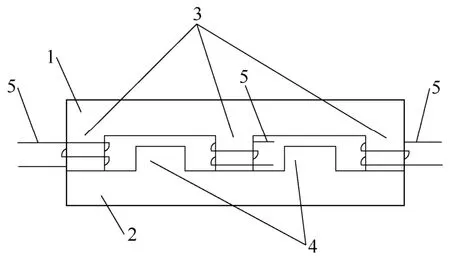
图3 三相“EΠ”形耦合电感Fig.3.Proposed “EΠ” core structure of 3-phase coupled inductors
3 三相EΠ形耦合电感器的磁路模型
为了建立三相“EΠ”形耦合电感的磁路模型,需要先分析其磁通分布。在忽略了各相绕组产生的通过外部空气的漏磁通和气隙边缘效应的情况下,得到“EΠ”形耦合电感的磁通分布如图4a所示。图中,φ1、φ2、φ3分别为通过各相绕组的主磁通,φC1、φC2、分别为通过“Π”形铁心两个磁柱气隙的漏磁通,N为各相绕组匝数。磁通所经过的各段路径长度如图4b所示,图中,w为绕组宽度,其值等于“E”形铁心的磁柱长度;g为“E”形铁心磁柱的气隙长度;gc为“Π”形铁心磁柱的气隙长度;a、c分别为铁心各部分的长度;l11、l12、l21、l22、l3、lc1、lc2为各部分磁路长度;d为“E”形铁心磁柱和“Π”形铁心磁柱之间的距离。
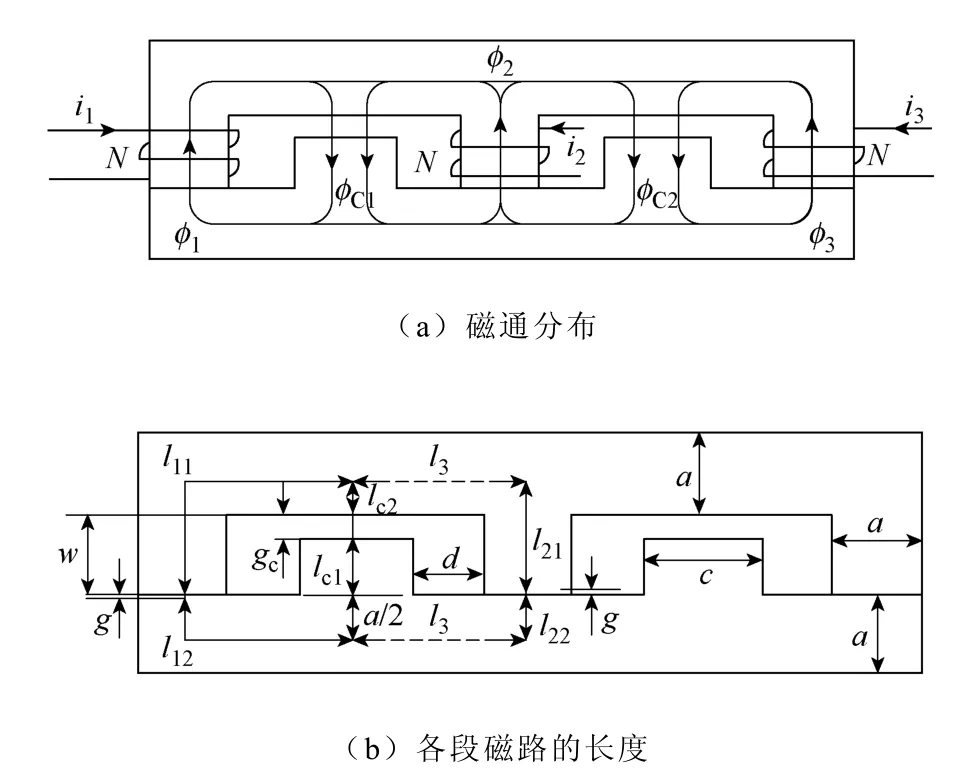
图4 磁通分布及各段磁路的长度Fig.4 Flux distribution and length of each magnetic circuit
根据磁路的欧姆定律可以得到三相“EΠ”形耦合电感的磁路模型如图5a所示。图中,Fj=Nij(j=1,2,3)为各相绕组的磁势;Rij(i,j=1,2)、R3、Rc1和Rc2分别为对应于图4b中各段磁路lij(i,j=1,2)、l3、lc1和lc2的磁阻。由于最右侧磁路的磁阻R31=R11,R32=R12,所以将R31用R11表示,R32用R12表示;Rg为气隙g的磁阻;Rgc为气隙gc的磁阻。将串联的磁阻合并,得到简化的磁路模型如图5b所示。
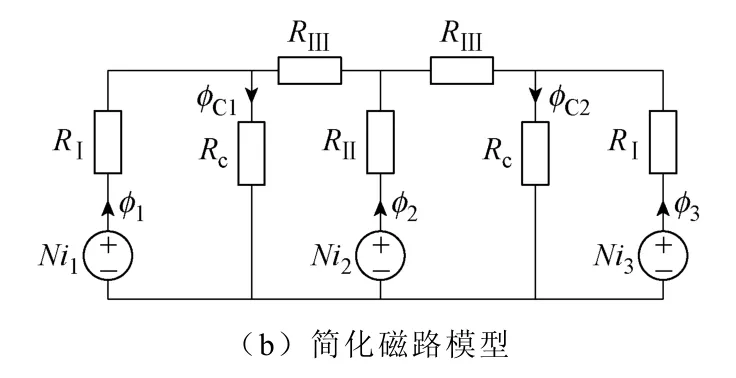
图5 三相“EΠ”型铁心的磁路模型Fig.5 3-Phase“EΠ”core’s simple magnetic circuit model
根据磁阻定义可得到图5a中各个铁心磁阻为
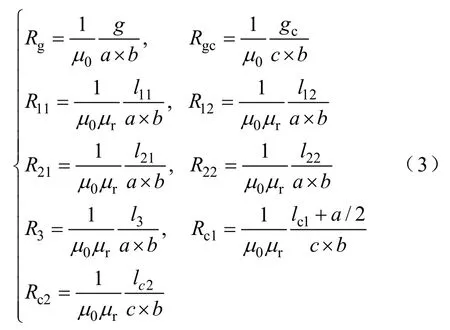
式中b——铁心长度;
μ0——空气磁导率;
μr——铁心材料的相对磁导率。
并有
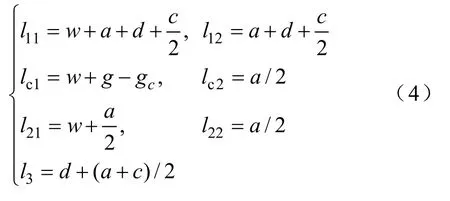
图5b中的磁阻RI、RII、RIII、Rc可以用图5a中的磁阻表示
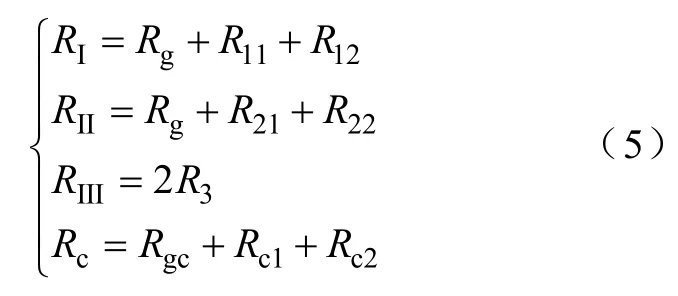
根据电感与磁阻的关系可得到图3中三相“EΠ”形耦合电感器的自感L(ii=1,2,3)和漏感Lki(i=1,2,3)
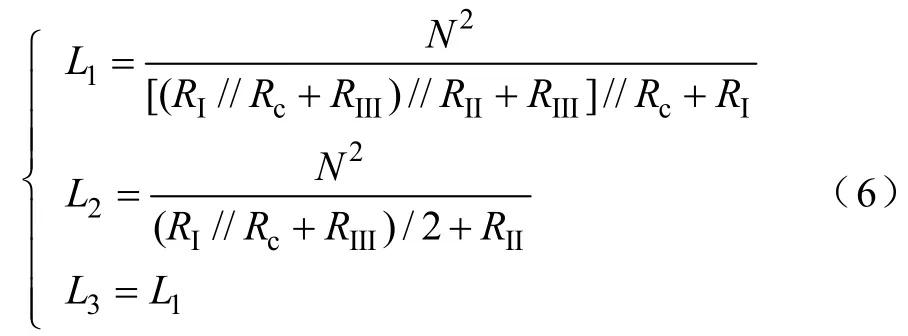

4 三相EΠ形耦合电感器磁路模型的改进
为了提高上述磁路模型的精度,需要考虑所忽略的“Π”形铁心气隙gc的磁场边缘效应和绕组外面空气的漏磁场。于是根据图5a得到三相“EΠ”形耦合电感的改进磁路模型如图6所示。图6与图5的区别在于:①磁阻Rgc包括了气隙gc的磁场边缘效应;②在各相的磁势源Ni1、Ni2和Ni3上分别并联了空气磁阻Rair1、Rair2和Rair3。下面分析这几个磁阻。
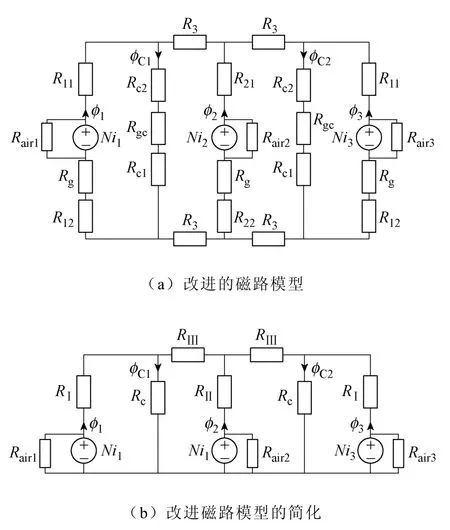
图6 三相“EΠ”形耦合电感器的改进磁路模型Fig.6.Improved magnetic circuit model of 3 phase “EΠ”core coupled inductors
4.1 “Π”形铁心的磁柱气隙磁阻Rgc
当考虑“Π”形铁心磁柱气隙gc的磁场边缘效应时,可求得磁柱气隙磁阻Rgc为[14]

4.2 绕组外面的空气磁阻Rair
对耦合电感器中间相绕组产生的外面空气磁场进行分析,可以得到其近似的磁力线分布如图7所示。图中的矩形底座表示缠绕着宽度为w的中间相绕组的“E”形铁心磁轭、磁柱和“Π”形铁心磁轭;对照图4b可知,宽度为w的绕组上、下两侧的铁心宽度均为a;带箭头的半圆弧线表示宽度为w的绕组产生的磁力线,半圆柱形表示磁力线通过的区域。
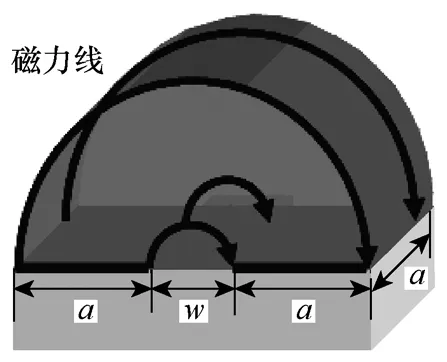
图7 耦合电感器中间相绕组的外面空气磁力线分布Fig.7 Flux distribution in the air out of coupled inductors’central winding
由图7并根据文献[15]的空间切割概念可得到耦合电感器各相绕组产生的磁力线区域如图8a所示,由于左、右两侧的绕组对称,所以只画了其中的一侧。图中,中间相绕组产生的磁力线所通过的区域包括上、下两部分,其磁力线所遇到的磁阻分别为Rt和Rb;中间相绕组的空气磁阻Rair2由Rt和Rb并联而成;两侧绕组产生的磁力线所通过的区域包括五部分,两侧绕组的空气磁阻Rair1和Rair3都由这五个区域的磁阻并联而成,其中上、下各有一部分与中间相绕组一样,呈半圆柱形,其磁阻也是Rt和Rb;绕组侧面还有一部分也呈半圆柱形,其磁阻为Rf;剩下的两部分呈1/4球形,上、下对称,其磁阻均为Rco。将图8a中的空气磁阻用集总参数模型表示,如图8b所示。于是可得各相绕组的空气磁阻Rair1、Rair2、Rair3
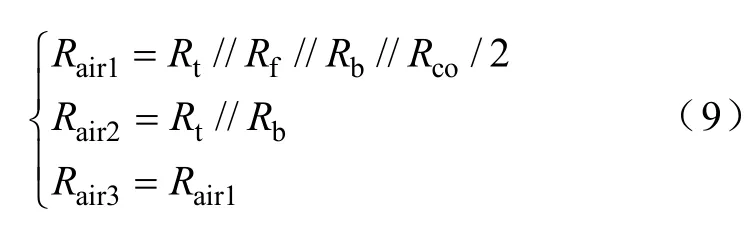
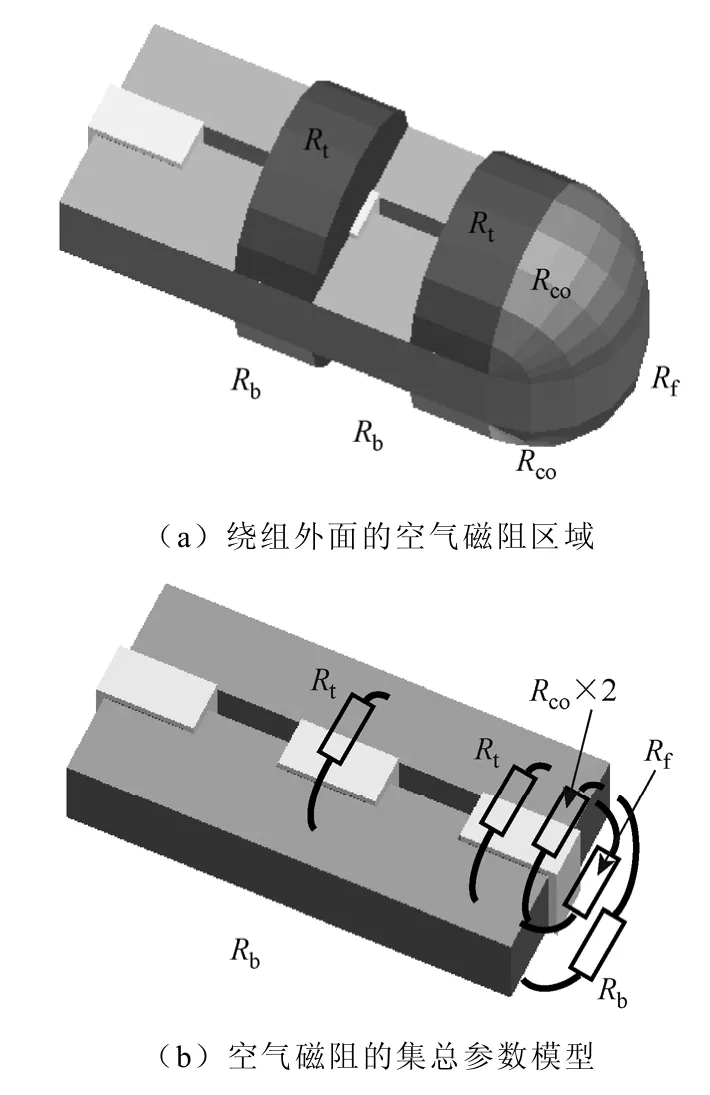
图8 耦合电感器绕组外面的空气磁阻Fig.8 Air reluctances out of coupled inductors’ windings
磁阻Rt和Rb的计算模型如图9所示,并有
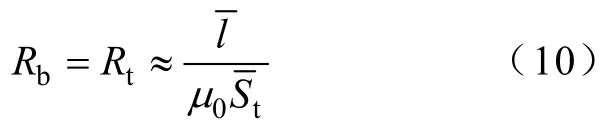
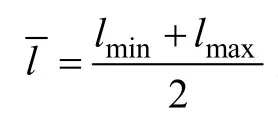
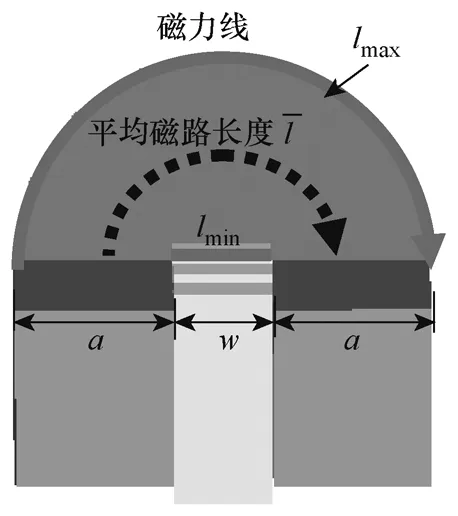
图9 磁阻“Rt”和“Rb”的计算模型Fig.9 Calculating model of reluctances “Rt” and “Rb”
同理,磁阻“Rf”的计算公式为

磁阻“Rco”的计算公式为

4.3 电感计算
得到各个磁阻的计算公式后,图6中改进磁路模型的绕组自感和漏感可按式(13)和式(14)计算

根据式(2)可求得互感
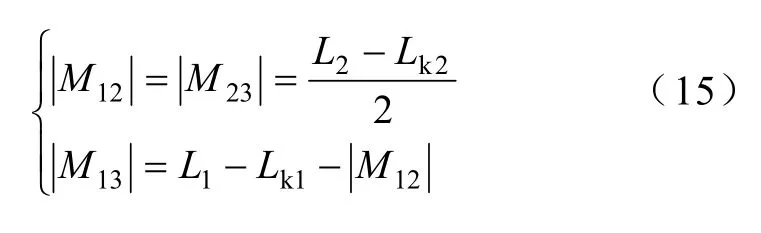
5 三相EΠ形耦合电感器的设计
在得到三相EΠ形耦合电感器的改进磁路模型后,可以对其进行设计,以下给出具体的设计方法。
5.1 设计规格
输入电压Vin;输出电压Vo;输出电流Io;开关频率fs;稳态输出纹波电流ΔIo,暂态电流响应速度Δi/ΔD。
5.2 自感和漏感计算
由于ΔIo和Δi/ΔD不一定能同时满足,在设计VRM时,应优先保证Δi/ΔD。为了满足Δi/ΔD,可求得漏感Lk为[3]
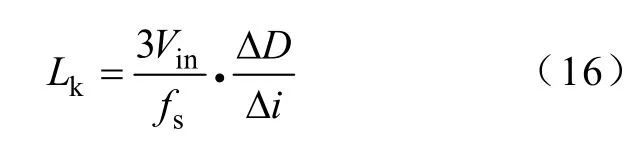
为了满足ΔIo,根据式(1)求得稳态电流纹波为
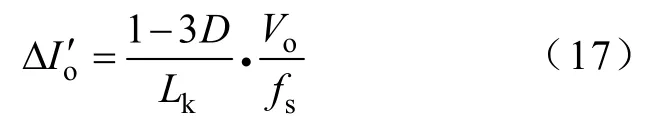

式中,k为耦合系数,-0.5≤k≤0。
5.3 绕组尺寸计算
在给定绕组电流密度J和每匝绕组厚度d1时,得到每匝绕组宽度w为:w=Io/(3d1J)。
5.4 铁心尺寸计算
“E”形铁心磁柱和“Π”形铁心磁柱的最大磁通密度分别为
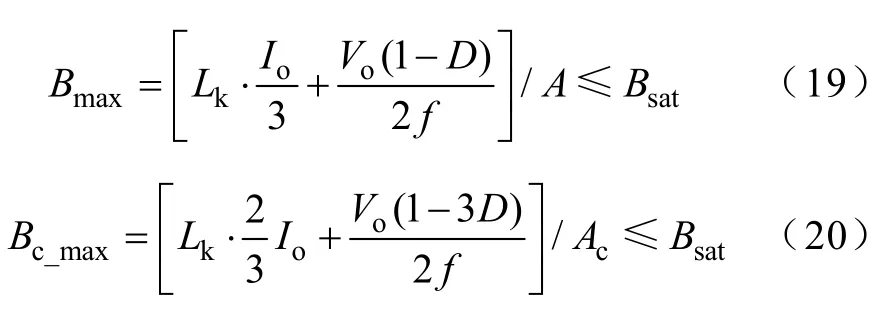
式中A——“E”形铁心的截面积;
Ac——“Π”形铁心的截面积;Bsat——铁心材料的饱和磁通密度。
由式(19)和(20)可得到A和Ac的值,进而根据AA==aa×bb和Ac==cc×bb得到a,b和c的值,如图4b所示。图中,“E”形和“Π”形铁心磁柱之间的距离d=N1d1+2δ,N1为绕组层数,d1为绕组厚度,δ表示在绕组与其窗口两侧之间所留的裕量。将式(16)和式(18)求得的漏感和自感代入式(13)和式(14),可以得到气隙长度g和gc,并有lc1=w+g-gc。
6 仿真与实验
6.1 样机设计与研制
本文设计了一个三相“EΠ”形铁心的磁集成耦合电感,设计规格为:输入电压Vin=12V,输出电压Vo=1.2V,输出电流Io=75A,开关频率fs=600kHz,稳态电流纹波ΔIo=0.4Io。根据上述设计步骤设计的磁心尺寸如表1所示,单位是mm,磁心材料采用Feroxcube公司的3F4型高频铁氧体。耦合电感的绕组匝数N=1匝,采用铜箔绕组,绕组宽度w=2.5mm,绕组厚度d1=0.4mm。实验样机如图10所示。

表1 三相“EΠ”形耦合电感的设计结果Tab.1 Design results of 3-phase “EΠ” core coupled inductors

图10 三相“EΠ”形耦合电感的样机Fig.10 Prototype of 3-phase “EΠ” core coupled inductors
6.2 仿真与实验
为了验证三相“EΠ”形耦合电感器结构的正确性及其磁路模型和设计方法的有效性,首先用磁路模型和改进的磁路模型分别计算了三相“EΠ”形耦合电感器的自感和漏感,然后用Ansoft公司的三维电磁场有限元分析软件(MAXWELL 3D FEA)进行了仿真,并采用Chenhua公司的3255型自动电子零件分析仪对实验样机进行了测试,该仪器的电感测试范围是0.1nH~9 999.9H,测试频率为1kHz,测试电压为1.2V。计算结果和测试结果如表2所示,由表2可见,改进磁路模型的精度较高,从而验证了该模型的有效性。在实际设计时,可以先用改进的磁路模型进行设计,如果有必要,再用3D FEA电磁场有限元分析软件进行仿真验证和优化设计。
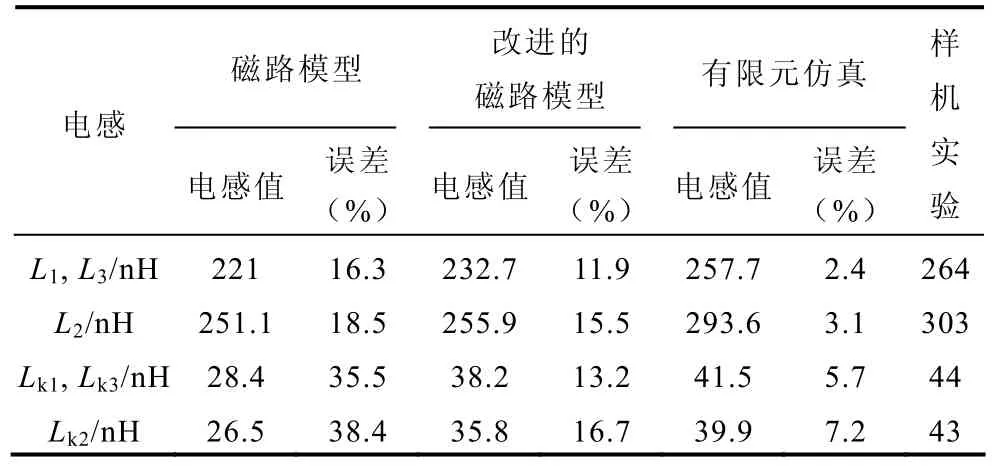
表2 电感的磁路模型计算值和有限元仿真值与实验值比较Tab.2 The inductances of calculation and 3D FEA simulation compared with experimental results
7 结论
(1)本文提出的三相“EΠ”形耦合电感器仅有两片磁心,其中一片呈传统的“E”形,另一片呈简单的“Π”形,具有磁心结构简单的优点;电感器的绕组长度只是包围“E”形铁心磁柱的长度,具有绕组长度小的优点;漏感的大小可通过改变“Π”形铁心磁柱长度进行调节从而调整VRM的暂态响应速度。
(2)本文建立的三相“EΠ”形耦合电感器的改进的磁路模型具有较高的精度,基于改进的磁路模型给出的设计方法具有充分的理论依据,可以用于三相“EΠ”形耦合电感器的设计。
(3)本文采用的电磁场有限元仿真软件可用于检验基于改进磁路模型所设计的三相“EΠ”形耦合电感器或进行优化设计。
[1] Intel Company.VRD11 DC-DC converter design guidelines[R].Http://www.intel.com,2006.
[2] Intel Corporation.Platform 2015: Intel Processor and platform evolution for the next decade[R].Intel White Paper,March 2005.
[3] Wong P,Xu P,Yang B,et al.Performance improvements of interleaving VRMs with coupling inductors[J].IEEE Transactions on Power Electronics,2006,16(4): 499-507.
[4] Li Jieli,Stratakos Anthony,Schultz Aaron,et al.Using coupled inductors to enhance transient performance of multi-phase buck converters[C].Proceedings of the IEEE Applied Power Electronics Conference,Anaheim,CA,2004: 1289-1293.
[5] Wu W,Lee N,George Schuellein.Multi-phase converter design with two-phase coupled inductors[C].Proceedings of the IEEE Applied Power Electronics Conference,Dallas,US,2006: 487-492.
[6] Xu Ming,Yan Dong,Lee Fred C.Multiphase voltage regulator having coupled inductors with reduced winding resistance: US,11/343,204[P].2006.
[7] 杨玉岗,李洪珠,王建林,等。可削减直流偏磁集成磁件在DC/DC变换器中的应用[J]。中国电机工程学报,2005,25(11): 50-54.Yang Yugang,Li Hongzhu,Wang Jianlin,et al.Research on the application of an integrated magnetics whose dc-bias can be reduced in DC/DC converter[J].Proceedings of the CSEE,2005,25(11): 50-54.
[8] Yang Yugang,Yan Dong,Lee C Fred.A new coupled inductors design in 2-phase interleaving VRM[C].Proceedings of the IEEE International Power Electronics and Motion Control Conference,Wuhan,China,2009: 344-350.
[9] 陈为,卢增艺,王凯.电压调节模块耦合电感性能分析与设计[J].电工技术学报,2009,24(1): 127-132.Chen Wei,Lu Zengyi,Wang Kai.Performance analysis and design of voltage regulator module with coupled inductors[J].Transactions of China Electrotechnical Society.2009,24(1): 127-132.
[10] 余建生,张波,刘学超.集成耦合磁路的新型电压调整模块[J].电工技术学报,2006,21(10): 94-100.Yu Jiansheng,Zhang Bo,Liu Xuechao.A novel voltage regulator module with integrated coupled magnetic path[J].Transactions of China Electrotechnical Society.2006,21(10): 94-100.
[11] 李洪珠,郝文慧,杨玉岗.无气隙可改变耦合度阵列式集成磁件在交错并联变换器中的应用[J].电工技术学报,2007,22(7):98-102。Li Hongzhu,Hao Wenhui,Yang Yugang.Application of changeable coupling degree array integrated magnetics with no air gap to staggered-shunt converter[J].Transactions of China Electrotechnical Society.2007,22(7): 98-102.
[12] 李洪珠,杨玉岗,荣德生,等.应用于四相电压调整模块的阵列式集成磁件[J].电工技术学报,2009,24(8): 77-83。Li Hongzhu,Yang Yugang,Rong Desheng,et al.Array integrated magnetics applied to 4-phase voltage regulator module[J].Transactions of China Electrotechnical Society.2009,24(8): 77-83.
[13] Roters H C.Electromagnetic Devices[M].John Wiley& Sons Inc,1943.
[14] Balakrishnan A,Joines W,Wilson T.Air-gap reluctance and inductance calculations for magnetic circuits using a schwarz-christoffel transformation[J].IEEE Transactions on Power Electronics,1997,12(4):654-663.
[15] Hoke A,Sullivan C R.An improved two-dimensional numerical modeling method for E-core transformers[C].Proceedings of the IEEE Applied Power Electronics Conference,Dallas,US,2002,1: 151-157.
