风力发电高塔系统风致动力响应分析

贺广零，李杰

(1.同济大学力学博士后流动站，上海市，200092;2.同济大学建筑工程系，上海市，200092)

0 引言

一般地，风荷载为风力发电高塔系统的控制荷载，多数倒塔事故均与风灾有关。对于风力发电高塔系统抗风设计，我国规范［1］依然沿用了拟静力分析方法。其中，桨叶风荷载仅简单地通过额定风速和修正系数来确定，这无疑存在一定风险。例如，2006年夏季的桑美台风，给浙江苍南风电场带来了毁灭性的破坏。该风电场共有28座风力发电高塔系统，总装机容量为15.85 MW，其中有20座遭到不同程度的破坏［2］。显然，拟静力分析法已难以满足结构设计的需要，风力发电高塔系统风致动力响应分析势在必行。已有部分研究者对风力发电高塔系统动力分析进行了研究，其进展主要体现在结构建模和桨叶风荷载建模2个方面。

风力发电高塔系统结构建模可分为整体建模和细部建模2种。在整体建模的研究中，Lobitz［3］将塔体和桨叶离散为多自由度质点系，通过连接矩阵实现桨叶和塔体耦合，并以有限元软件Nastran为平台进行了风致动力响应分析。Murtagh等［4］亦将桨叶和塔体离散为多自由度质点系，但桨叶和塔体之间的耦合通过轮毂处的剪力传递来实现，忽略了轴力、弯矩和扭矩的影响。显然，Lobitz和Murtagh等提出的结构模型过于粗糙，对结构细部重视不够，无法体现应力集中、结构局部屈曲等现象，从而难以全面把握结构动力响应。随着研究的深入，一些学者对细部建模日益重视。Bazeos等［5］和 Lavassas等［6］分别完成了450 kW和1 MW风力发电高塔系统支撑结构(塔体和基础)的细部建模。其中，塔体和基础分别采用壳体和实体单元模拟，并对加劲肋、法兰和开洞进行了建模，甚至考虑了土－结构相互作用的影响。然而，Bazeos等和Lavassas等却未对桨叶进行建模，自然难以考虑桨叶和塔体之间的耦合作用。总体上，整体建模引入了桨叶和塔体耦合机制，但细部结构过于粗糙。与之相反，细部建模能够进行较为精确的细部分析，但忽略了桨叶和塔体耦合作用，必然会对桨叶传递给塔体的荷载作出一定的假设。因此，有必要综合整体建模和细部建模的优势，提出风力发电高塔系统一体化、精细化结构模型。

在风力发电高塔系统桨叶风荷载建模进展中，各种繁简不一的风速功率谱模型相继出现。其中，绝大部分风速功率谱模型［7-8］仅考虑了风场空间中固定一点的结构特征，而未考虑桨叶的旋转效应。实测结果表明，与静止点上测得的紊流风谱相比，旋转桨叶上动点测得的紊流风谱能量分布发生了根本性的变化，这种效应即为桨叶旋转效应，考虑了桨叶旋转效应的紊流风速功率谱即为旋转样本谱［9］。迄今为止，主要有2类重要的旋转样本谱模型:PNL模型［10-11］和SNL模型［12-13］。事实上，PNL模型和SNL模型对桨叶旋转效应物理本质和物理意义的把握均未抓住重点。更为重要的是，两者都是基于经典随机过程的数值特征描述方式进行建模。本质上，这是一种现象学建模方式，必然具有只能反映随机过程的数值特征(主要是方差)而难以描述随机过程的细部特征与结构、引入平稳过程的概念和各态历经假定、随机过程与其样本描述之间的关系不清晰等一系列局限性［14］，也很难正确解决随机动力系统分析的一系列问题，如结构非线性随机响应分析、结构动力可靠性评价等。因此，有必要在准确把握桨叶旋转效应物理本质和物理意义的基础上，对脉动风速这一典型随机过程，基于更为合理的描述方式构建旋转风速谱物理模型，以避免现象学建模的诸多局限性。

为了正确分析风力发电高塔系统的风振动力响应，本文以典型的1.25 MW风力发电高塔系统为背景，建立了风力发电高塔系统“桨叶－机舱－塔体－基础”一体化、精细化有限元模型。然后，基于随机过程的随机函数描述，提出了旋转Fourier谱物理模型，结合随机Fourier谱物理模型，依据随机函数法实现了风力发电高塔系统风场模拟。最后，以大型有限元分析软件ANSYS为平台，完成了风力发电高塔系统风致动力响应分析，并与静力分析进行了对比。

1 风力发电高塔系统一体化有限元模型

所谓风力发电高塔系统一体化三维有限元模型，是指将桨叶、机舱、塔体和基础同时建模，以模拟不同构件(尤其是桨叶与塔体)之间的相互耦合作用，并反映结构应力集中、局部屈曲等细部特征。本文以典型的1.25 MW三桨叶变桨距风力发电高塔系统为研究载体，建模平台为大型通用分析软件ANSYS。

1.1 桨叶建模

风力发电高塔系统风轮直径为64.35 m，3片桨叶具有循环对称性。鉴于桨叶结构异常复杂，其截面形状和扭角均沿展长持续变化，按照实际尺寸进行建模，存在无法收敛和计算效率极低等诸多问题，故有必要先对其进行等效处理。本文采用刚度等效原则，构建了变刚度壳体(SHELL181)桨叶模型。采用该单元主要基于:(1)能模拟变刚度壳体;(2)可考虑大变形效应;(3)壳体单元比实体单元具有更高的计算效率;(4)塔体1个方向的尺寸与另外2个方向的尺寸相差较大，用壳体单元模拟不容易出现畸形网格;(5)能模拟旋转桨叶应力刚化效应。

1.2 机舱及内部结构建模

机舱是风力发电机组中主要的承载部件，对机舱内的所有设备(包括齿轮箱、发电机等)及其附属部件起到固定和支撑作用。机舱长9.8 m，宽3.22 m，高3.01 m，质量68.5 t。机舱内部结构非常复杂，对所有构件进行细部建模难度极大，且分析精度提高有限。与细部建模对比计算表明，将机舱及其内部构件视为一个整体，依据刚度等效原则，借助三节点二次三维梁单元(BEAM189)来模拟即可达到很高的精度。采用该单元的主要原因是:(1)适合深梁结构分析。该单元基于Timoshenko梁理论，考虑了剪切效应的影响。机舱宽长比为 3.22/9.8=0.33 ＞0.25，不宜采用Euler梁进行分析。(2)除了3个方向位移和扭转共6个自由度外，还增加了1个翘曲自由度，可进行大转动、大应变非线性分析。机舱在工作状态下会产生显著的翘曲和扭转，因此在分析过程中应打开翘曲自由度。如果用Euler梁模拟机舱变形，且不考虑翘曲自由度，所得结果会严重偏离真实值。(3)存在应力刚度项，可进行弯曲、横向和扭转稳定性分析。

1.3 塔体建模

风力发电钢塔由3节塔段构成，塔段之间通过法兰连接，塔体厚度呈非线性变化。钢塔高66.35 m，塔底直径 3.9 m，塔底厚度 0.02 m，塔顶直径2.55 m，塔顶厚度 0.012 m，弹性模量 2.1 ×1011Pa，密度 7850 kg/m3。跟桨叶一样，塔体也采用SHELL181单元进行建模。

钢筋混凝土风力发电塔为自行研发和设计，塔高66.35 m，塔底直径3.9 m，塔底厚度0.3 m，塔顶直径2.55 m，塔顶厚度0.2 m;混凝土标号 C30，弹性模量3 ×1010Pa，泊松比 0.2;钢筋为 HRB335，弹性模量2.1× 1011Pa，泊 松 比 0.3。 采 用 复 合 壳 单 元(SHELL181)对钢筋混凝土风力发电塔进行有限元建模。复合壳单元可用来模拟由多层复合材料所组成的结构，定义该单元时需要给出每层材料的属性和厚度。在应用该单元之前，首先必须对钢筋混凝土风力发电塔进行弥散分层处理。可将塔身沿壁厚方向分为5层，即内外混凝土保护层、内外纵向受力钢筋层和2层钢筋之间的混凝土层。混凝土层的厚度取实际厚度，结构中离散的钢筋则按照面积等效原则弥散成厚度不变的钢筋层，层与层之间按照实际结构顺序排列(图1)。在建模过程中，将塔身分成4段，每段根据塔身的实际配筋情况赋以具有不同厚度的钢筋层。自下而上4段的纵向钢筋总配筋量(包括外排纵向钢筋和内排纵向钢筋)分别为78716、64468、51516和 26788 mm2。

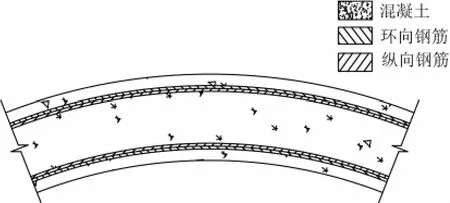
图1 钢筋混凝土塔横截面分层图Fig.1 Cross section of concrete wind turbine tower

1.4 基础建模

塔底采用10 m×10 m×1.80 m的圆截面钢筋混凝土筏基。基础之下土体的泊松比0.3，密度2100 kg/m3，剪切模量5.2×108Pa。基础厚度与半径之比为1.80/10=0.18＞1/15，故采用实体单元模拟较为合适。Solid65单元是专为混凝土、岩石等抗压能力远大于抗拉能力的非均匀材料开发的单元。由于增加了钢筋混凝土特有的材料参数和整体式钢筋模型，故而在钢筋混凝土三维实体建模方面具有优势。此外，Solid65单元具备拉裂、压碎、塑性变形和蠕变的能力，因此能够较好地模拟钢筋混凝土的开裂、压碎现象。

1.5 构件组合

在风力发电高塔系统模型中，存在着桨叶、机舱、塔体、基础4个基本构件。不同构件的结构尺寸、所采用的单元类型不一样，构件之间的网格密度因为拓扑形状各异而难以达到完全一致。因此，不同构件之间的连接成为有限元建模的难点，本文采用多点约束单元(MPC184)来实现不同构件之间的连接。MPC184单元为基于约束方程理论的一种单元形式，具有约束方程的优势:能够完成不连续、自由度不协调的单元网格之间的过渡，而无需边界节点一一对应。在建模过程中，MPC184单元实现了梁、板壳和实体单元之间的组合，完成了风力发电高塔系统“桨叶－机舱－塔体－基础”一体化建模，有效地解决了构件之间的滑移问题。根据效率与精度均衡的原则，风力发电钢塔和钢筋混凝土风力发电塔分别划分了1098和1608个单元。

2 风力发电高塔系统风速场

风力发电高塔系统风速场可分为2个部分:桨叶风速场和塔体风速场。其中，桨叶风速场必须考虑桨叶旋转效应，宜依据旋转Fourier谱来描述;而塔体风速场无需考虑该效应，可根据随机Fourier谱来刻画。

事实上，无法也无需对模型中所有点进行风场仿真。在本文中，对风力发电高塔系统整体结构进行离散，每片桨叶等效为3个均匀分布的集中质点，3片桨叶共9个集中质点。塔体(机舱)离散为非均匀分布的6个集中质点，各点的具体位置见图2。等效集中质点为动力计算时需要输入风速时程的计算点，本文主要进行这些点上的风速时程模拟。

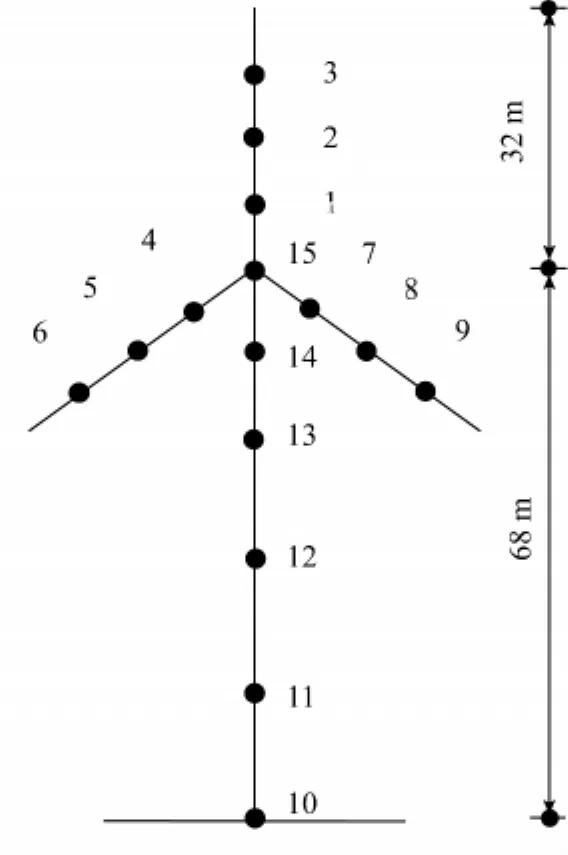
图2 风力发电高塔系统简化计算模型Fig.2 A Simplified computing model of wind turbine system

2.1 塔体风速场

2.1.1 平均风速

平均风速沿高度变化可通过风速廓线函数(在风能技术领域，一般称之为风剪模型)来表述。风剪模型通常有指数律模型和对数律模型2种。其中，指数律模型在工程中最为常用，表达式为

式中:vs(z)、v10分别为离地高度 z处、参考高度(10 m)处的平均风速;α为风剪系数，依据Germanischer Lloyd 规范［14］取 0.14。利用式(1)，可算出各代表点处的平均风速，计算结果见表1。

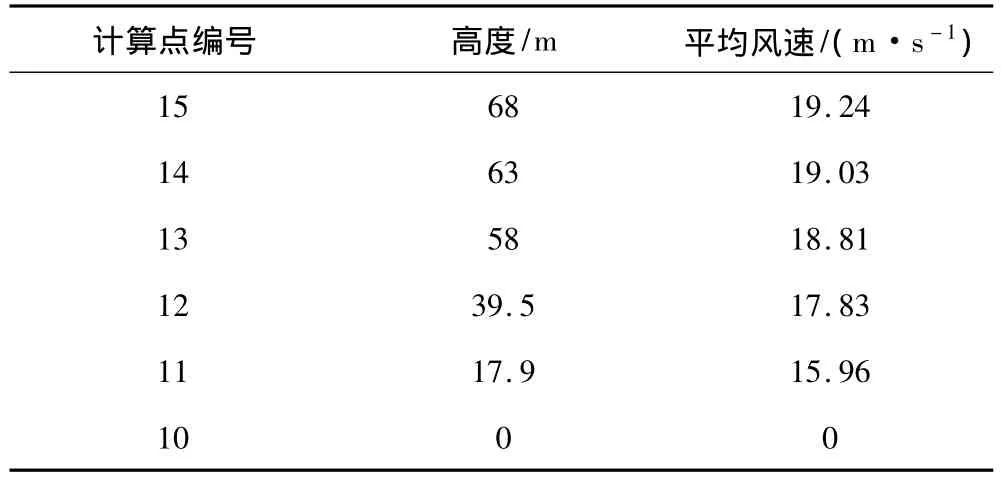
表1 塔体各计算点处平均风速Tab.1 Mean wind velocities at sampling computing points of wind turbine tower

2.1.2 脉动风速

现有的绝大部分风速谱均基于经典随机过程的数值特征描述方式进行建模。这种现象学建模方式，必然具有只能反映随机过程的数值特征而难以描述随机过程的细部特征与结构等一系列局限性。事实上，存在另一类随机过程描述——随机函数描述。在这一描述中，定义过程 X={x(η，t)，t∈T}，对于样本空间Ω，每固定η=θ∈Ω，即得到1个普通的实函数x(θ，t)，称为样本函数。换句话说，x(η，t)是1 个取值于可测空间R的随机函数。在这样一个描述中，样本与其解析描述——随机函数之间存在明晰的逻辑联系。而样本函数x(θ，t)，则揭示着具体物理过程x与其原因变量θ之间的物理关系。通过研究这一物理关系并进行建模，可以建立基于物理的随机过程模型。有鉴于此，随机 Fourier谱［15］可定义为

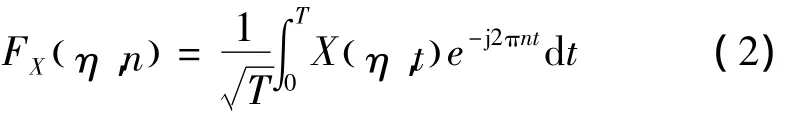
式中:T为样本持时;随机过程X(η，t)是样本x(t)的集合;η为影响随机激励发展过程且具有物理意义的随机变量或随机向量。根据各向同性紊流理论，可确定随机Fourier谱的基本表达式。依据随机建模准则，由310组实测风速数据记录，可以给出基本随机变量的概率分布和待定拟合参数的具体值，并最终确定随机Fourier谱［16］的表达式为

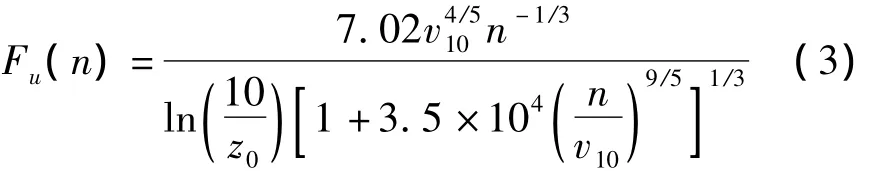
式中v10和z0为随机变量，分别服从极值I型分布和对数正态分布。因为塔体无需考虑桨叶旋转效应，其上任意一点处脉动风速的随机特性可以通过随机Fourier谱来体现。而在垂直平面上的任意2点之间的相关性则可以通过随机Fourier互谱来反映，其表达式可以由2点处的随机Fourier谱与随机相干函数的乘积确定，即

式中γu1u2(n)为相干函数。因为风力发电高塔系统塔体为长细比较大的高耸结构，故可忽略水平向风速的相关性，相干函数γu1u2(n)的表达式可简化

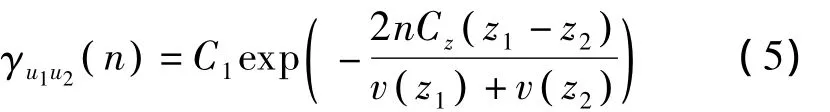
式中v(z1)和v(z2)分别为高度为z1和z2的2点处的平均风速，可按指数律由基准高度(一般为10 m)处平均风速换算得到。

本文采用随机函数法实现风场仿真，亦即对随机函数物理模型(随机Fourier谱物理模型)进行逆Fourier变换，即可得到各计算点的脉动风速时程

式中:j=1，2，…，k;Ijm为随机 Fourier谱矩阵Cholesky分解后的下三角矩阵元素;φ0ml为随机初相位角，在(0，2］区间取值;Δφml为相位差谱［17］;nml为双索引频率。值得强调的是，对于本文提出的随机函数法而言，随机Fourier谱与脉动风速时程存在一一对应关系，这点与谱表现法存在本质区别。

当随机Fourier的随机变量皆取平均值时可得到均值参数谱。显然，均值参数谱是具有代表性的样本Fourier谱。本文风力发电高塔系统所在场地的v10均值为14.71 m/s，地面粗糙度 z0均值为 0.029 m，利用快速傅里叶变换编制Matlab程序完成塔体脉动风场仿真的计算。图3给出了计算点11～15处的仿真脉动风速时程。不难发现，不同点风速时程之间存在一定的相关性，且不同点风速时程之间的相关程度并非一致，其相关程度随着2点距离的增加而减少。例如，相邻点风速时程之间的相似程度要大于非相邻点风速时程之间的相似程度。

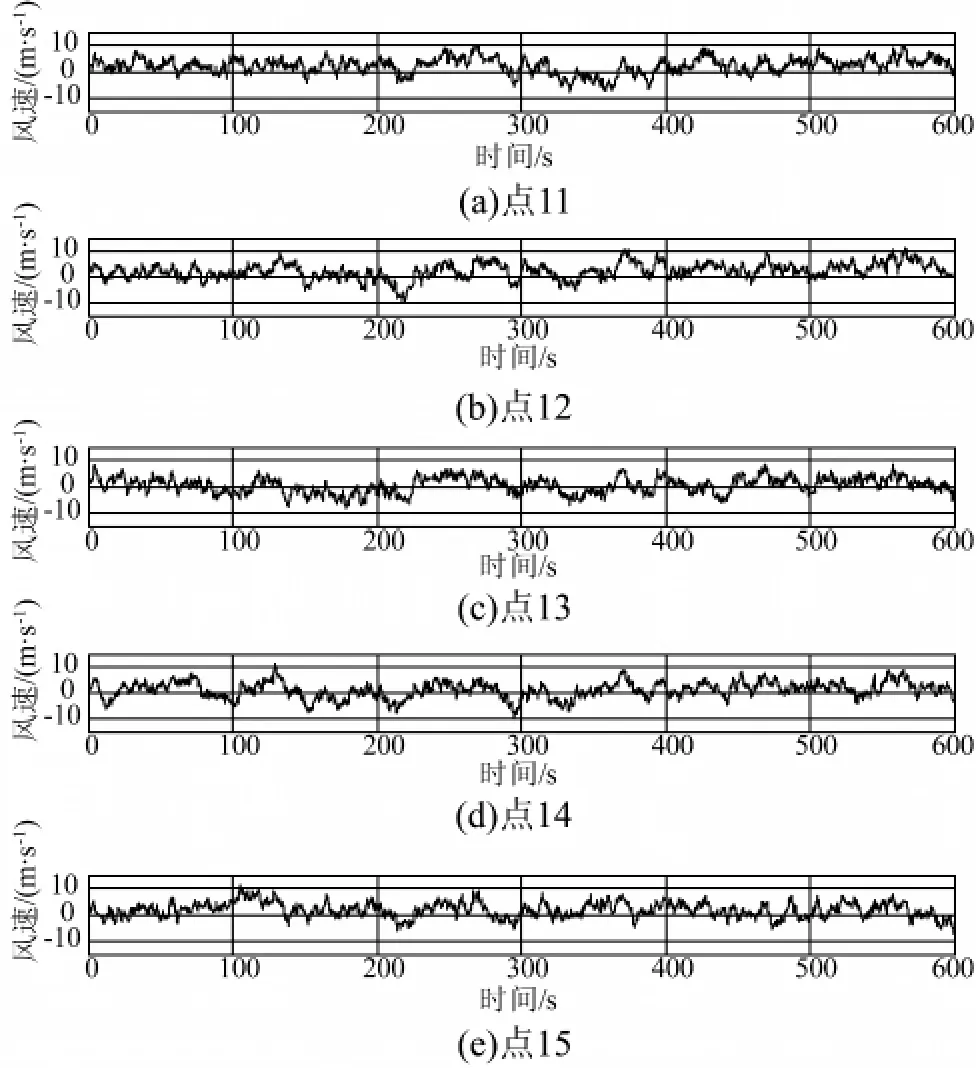
图3 塔体各计算点处的仿真脉动风速时程Fig.3 Fluctuating wind velocities at sampling computing points of wind turbine tower

2.2 桨叶风速场

2.2.1 平均风速

事实上，桨叶旋转效应会对平均风速场产生一定的影响，其本质上为风剪效应所致。对于旋转桨叶上的任意1点，其高度z因桨叶旋转而呈现周期性变化，其表达式为

式中:r为计算半径，指风轮旋转平面内任意1点与轮毂中心之间的距离;φ=Ω t为该点在风轮平面的方位角，正上方时为0°，Ω为桨叶旋转速度。将(7)式代入(1)式，可得旋转桨叶上半径r处的平均风速为

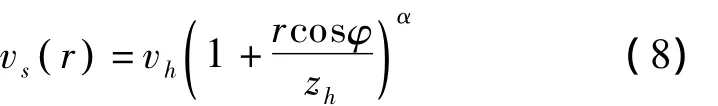
将10 m 高平均风速14.71 m/s，风剪系数0.14，轮毂高度68 m代入式(8)中，可获得轮毂处的平均风速vh为19.24 m/s。又已知1.25 MW 风力发电机在正常运行情况下的转速约为21.1 r/min(0.352 Hz)，则角频率 ω =2πn=2.21 rad/s，相位角 φ =ωt。将上述参数代入式(8)中即可确定桨叶上各点的平均风速。图4给出了计算点1、2、3、6、9处的平均风速时程，一般地，模拟风速的持续时间为600 s。为了显示清晰，本章只给出了0～30 s的平均风速时程，其他时段满足相同的规律。总体上，旋转桨叶上各点的平均风速有如下特点:(1)平均风速不再为定值，而呈谐波规律变化;(2)计算点半径越大，风速变化的幅度越大，如点2的变化幅度大于点1，点3的变化幅度大于点2;(3)不同桨叶之间风速不同步，相邻桨叶之间存在2π/nb(nb为桨叶数目)的相位差。桨叶123的相位要落后于桨叶456，桨叶456的相位要落后于桨叶789，且其间的相位差均为2π/3。

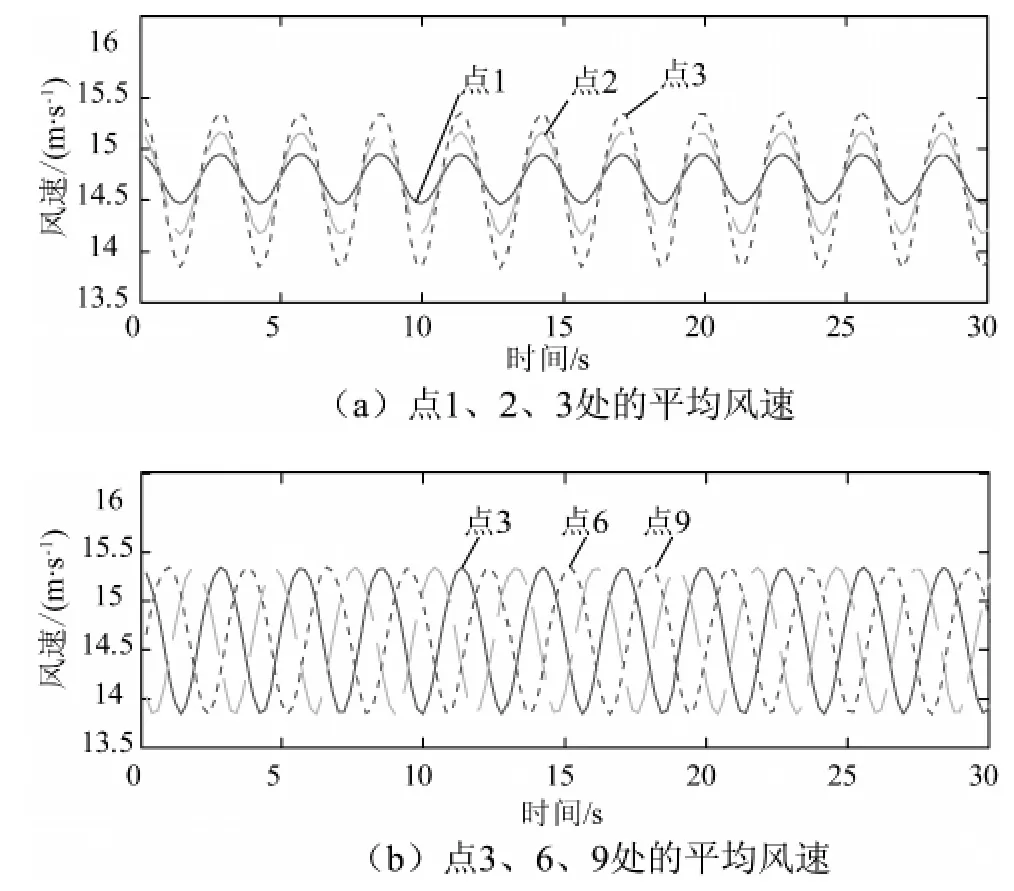
图4 计算点处的平均风速时程Fig.4 Mean wind velocities at sampling computing points

2.2.2 脉动风速

桨叶旋转效应不仅对平均风速场产生干扰，而且对脉动风速场也会产生重要影响。本文采用基于物理机制的旋转Fourier谱来考虑脉动风速的桨叶旋转效应。

一般地，风场是一个时变随机场，空间中任意一点的风速不仅与该点的空间位置坐标有关，而且还与时间有关。此外，风力发电机桨叶风场还具有其特殊性:桨叶上任意一点的空间位置随着桨叶旋转而不断变化，从而导致旋转桨叶风场还具有空间变化性。总体上，旋转桨叶风场具有时间、空间双重变化性。为了准确描述作用在旋转桨叶上的风速时程，首先需要将直角坐标系转换至旋转坐标系。在空间上，可有规律地在风轮平面上选取采样点。在旋转桨叶历经采样点时，提取该采样点在该时刻的风速，依此类推，按时间顺序排列可获得1组新的风速时程，基于这组风速时程构建的随机Fourier谱即为旋转Fourier谱。显然，这组风速时程一直作用在桨叶上。在明确旋转Fourier谱物理机制的基础上，可得出2个结论:(1)从定性上分析，旋转Fourier谱能更准确地预测风力发电机极值荷载和疲劳荷载。旋转Fourier谱反映了风速作用在桨叶上的物理机制，不仅体现了风速自身的脉动特性，而且刻画了桨叶高度周期性变化引起的风速波动。(2)旋转Fourier谱的明显优势是可将桨叶旋转这一运动学问题转化为静力学问题。因为旋转Fourier谱已经考虑了桨叶旋转效应，基于该谱进行风力发电高塔系统风致动力响应分析时无需再考虑该效应。

不难证明，样本互相关函数与Fourier互谱为Fourier变换对。对Fourier互谱进行逆Fourier变换，可得2点间的互相关函数为

与式(4)不同的是，γ(d(τ))为旋转坐标系下的相干函数［18］;Fx(n) 为随机 Fourier谱。

依据旋转Fourier谱的物理机制，旋转桨叶上任1点在不同时刻的自相关函数可用2点间的互相关函数来代替，其表达式为

对旋转自相关函数进行Fourier变换，可得到旋转Fourier谱

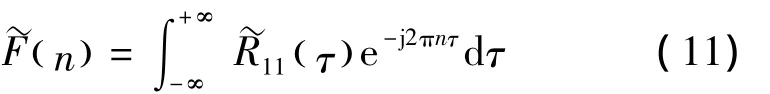
将式(9)、(10)代入式(11)中，得到

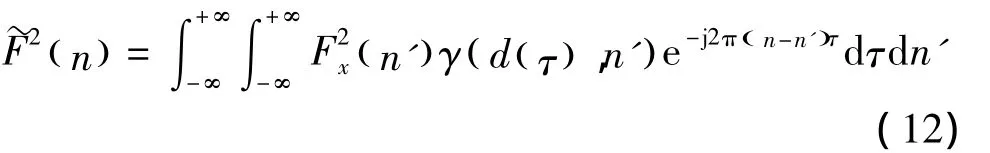
为了分析方便，可将γ(dτ)，(n)′进行Fourier级数展开，

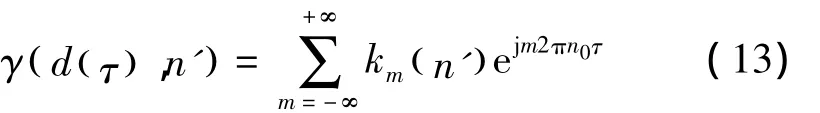
式中:n0为桨叶转动频率;km(n)为 Fourier展开系数，

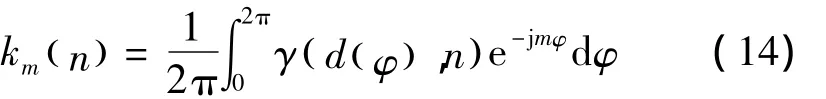
式中 φ =2πn0τ。将式(13)代入式(12)中，得

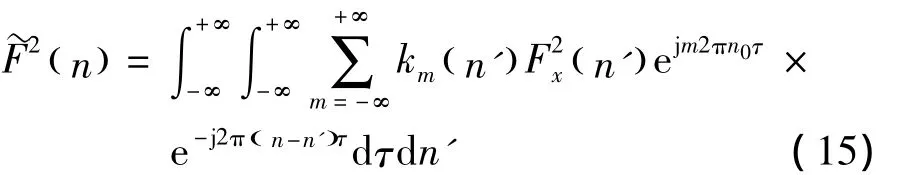
根据δ函数的性质，可得

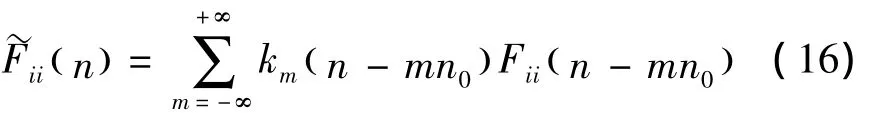
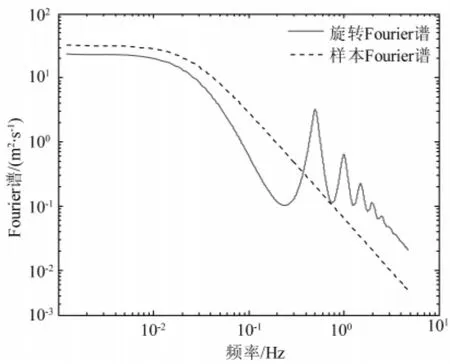
图5 旋转Fourier谱(样本)与随机Fourier谱(样本)比较Fig.5 Comparison between the rotational spectrum ＆the random one

事实上，旋转Fourier谱为作用在旋转桨叶上的风速时程经过Fourier变换所得，是一种自身蕴含了桨叶旋转效应的紊流风速谱。图5给出了旋转Fourier谱(样本)与随机Fourier谱(样本)之间的比较。相比较而言，旋转Fourier谱的能量由低频向高频转移，并在桨叶转动频率的整数倍处出现峰值。由式(16)可知，旋转Fourier谱(n)可由无穷多个随机Fourier谱Fii(n)经过桨叶旋转频率n0整数倍平移之后叠加而成。这样，就容易理解为什么旋转Fourier谱在旋转频率整数倍处会出现多峰现象。

为了考虑旋转桨叶上不同点风速之间的相关性，可构建旋转Fourier互谱

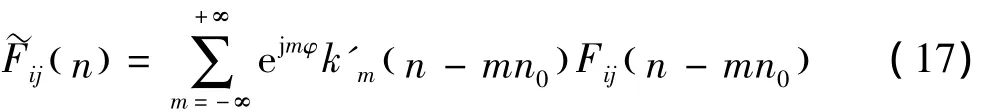
值得注意的是，桨叶上2点处脉动风速的旋转Fourier互谱与塔体上2点处脉动风速的随机Fourier互谱有本质的不同，主要体现在2个方面:(1)旋转Fourier互谱必须在旋转坐标系下考虑2点处脉动风速的相关性。在旋转坐标系下，2点处脉动风速的互谱已经不能简单地通过各点处脉动风速的自谱与相干函数的乘积来确定。(2)旋转Fourier互谱体现了桨叶上，而非风轮平面上，任意2点处脉动风速之间的相关性。因此，旋转Fourier互谱可分为同一桨叶上2点之间的旋转Fourier互谱和不同桨叶上2点之间的旋转Fourier互谱。

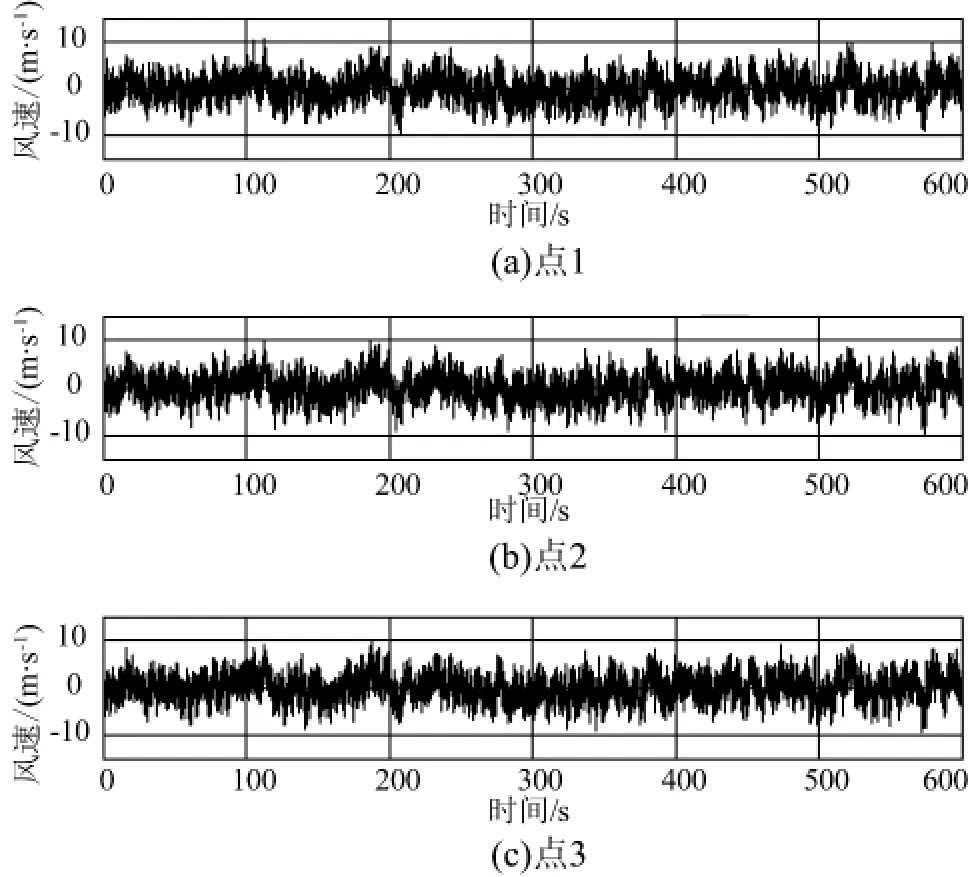
图6 计算点1、2、3处的脉动风速时程Fig.6 Fluctuating wind velocities at sampling computing points 1，2 and 3

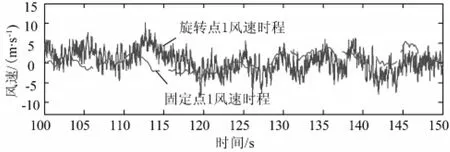
图7 旋转点风速时程与固定点风速时程比较(100～150 s)Fig.7 Fluctuating wind velocity comparison between the rotational point＆the stationary onepoint(100～150 s)

相似地，基于旋转Fourier谱模型，同样可以依据式(6)进行桨叶风场仿真。图6给出了计算点1～3处的仿真脉动风速时程，其他桨叶上的风速时程相似，本文不赘述。图7给出了固定点风速时程(基于随机Fourier谱的风速时程)与旋转点风速时程(基于旋转Fourier谱的风速时程)之间的比较。相比较而言，基于旋转Fourier谱的风速时程具有2个基本特点:(1)风速时程幅值较大，但不具有明显优势;(2)风速时程振动频率有大幅度提高，这点极为显著。其主要原因在于旋转点风速时程不仅体现了风速自身的脉动特性，而且还刻画了旋转桨叶高度周期性变化引起的风速改变。总体上，塔体上某点的脉动风速具有时变性，而旋转桨叶上某点的脉动风速时程具有时变、空变双重性。从频谱的角度看，相对于随机Fourier谱而言，旋转Fourier谱在高频段的能量更为丰富，其对应的脉动风速时程振动频率自然更高。总之，在考虑桨叶旋转效应之后，桨叶脉动风速时程幅值存在一定增长，振动频率会有大幅度提高，从而必然会对风力发电高塔系统极值荷载和疲劳荷载产生重要影响。这正是研究桨叶旋转效应，提出旋转Fourier谱的根本意义所在。

3 风荷载计算

3.1 塔体风荷载计算

对于塔体而言，可借鉴建筑结构领域的相关研究成果确定风荷载。如果作用在塔体上的紊流风速为v( z)，根据Bernoulli定理，塔体表面上高度z处某点上作用的风压可以表示为

式中:Cp为该点对应的压力系数;ρ为流体密度;v(z)为总风速。

3.2 桨叶风荷载计算

一般来说，桨叶结构是异常复杂的，其复杂性主要体现在2个方面:其一，桨叶截面形状持续变化;其二，桨叶截面扭角不断变化。如何准确且简单地确定作用在复杂结构上的风荷载是个棘手的问题，事实上，该问题一直困扰着风工程界。此外，桨叶在旋转过程中会对风场进行干扰，从而减缓作用在结构上的风速。基于此，本文引入了被广泛接受的叶素动量(blade element momentum)理论［11，19］，以准确而简单地确定作用在桨叶上的风速，并考虑旋转桨叶对风速的减缓作用。

4 风致动力响应分析

在模态分析的基础上，根据上述风荷载时程，利用有限元动力分析方法，分别对风力发电钢塔和钢筋混凝土风力发电塔进行了风致动力响应分析。在分析过程中，2种塔体均采用瑞利阻尼［20］。其中，风力发电钢塔阻尼比为2%，钢筋混凝土风力发电塔为5%。

4.1 风力发电钢塔

作为特殊的高耸结构，风力发电塔的最大位移理论上应发生在塔顶，而最大弯矩应发生在塔底，这一点在动力分析结果中得到了验证。风力发电塔顺风向塔顶位移动力响应如图8(a)所示，基底弯矩动力响应如图8(b)所示。从图8中可看出，基底弯矩最大值为49708 kN·m，塔顶位移最大值为0.891 m。风力发电钢塔动力响应出现了显著的“拍振”现象，从而带来过大的振动，降低了结构的可靠性，这在工程上是不允许的。一般地，产生“拍振”的物理机制是:存在大、小2种质量，其频率很接近且耦合很小，于是大质量振动就激发小质量共振，能量逐步传送到小质量上，使其发生很激烈的振动;然后，小质量的振动能量又逐渐输送回到大质量，使其振动加剧，如此往复不已，称为能量的游荡［21-22］。对于风力发电钢塔而言，桨叶为小质量(单片桨叶质量约为4.3 t)，塔体(包括机舱)为大质量(总质量约为157 t)，且桨叶与塔体(包括机舱)振动频率相近，故存在显著的“拍振”现象。为了消除“拍振”现象，一项可行的措施是改变风力发电钢塔塔体的刚度。事实上，1.25 MW风力发电钢塔结构已经偏柔［23］，若继续降低塔体刚度很可能会导致结构安全问题，唯有提高塔体刚度方是两全之策。增大塔体半径和壁厚是增大结构刚度比较理想的办法，但是两者所需付出的经济代价往往让人难以接受。相比较而言，钢筋混凝土风力发电塔因自身刚度较大，则有望消除“拍振”现象，降低结构响应。以下将对钢筋混凝土风力发电塔进行风致动力响应分析。

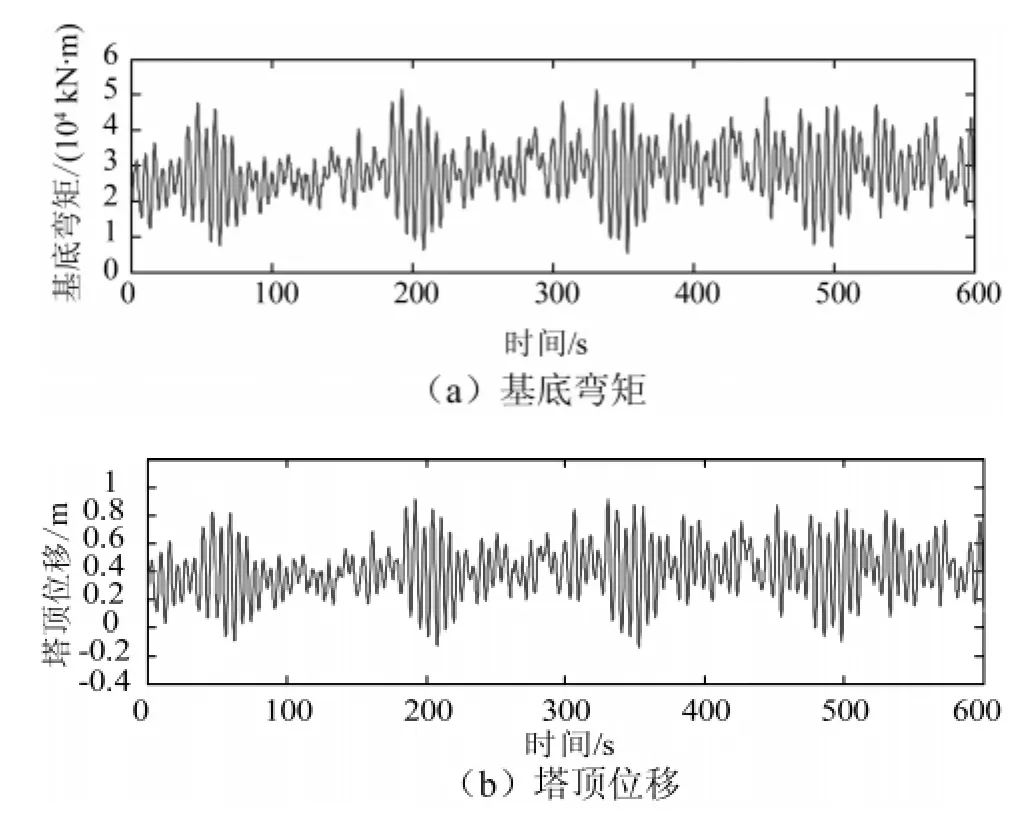
图8 风力发电钢塔基底弯矩与塔顶位移动力响应Fig.8 Tower base bending moment response and tower top displacement response of steel wind turbine tower

4.2 钢筋混凝土风力发电塔

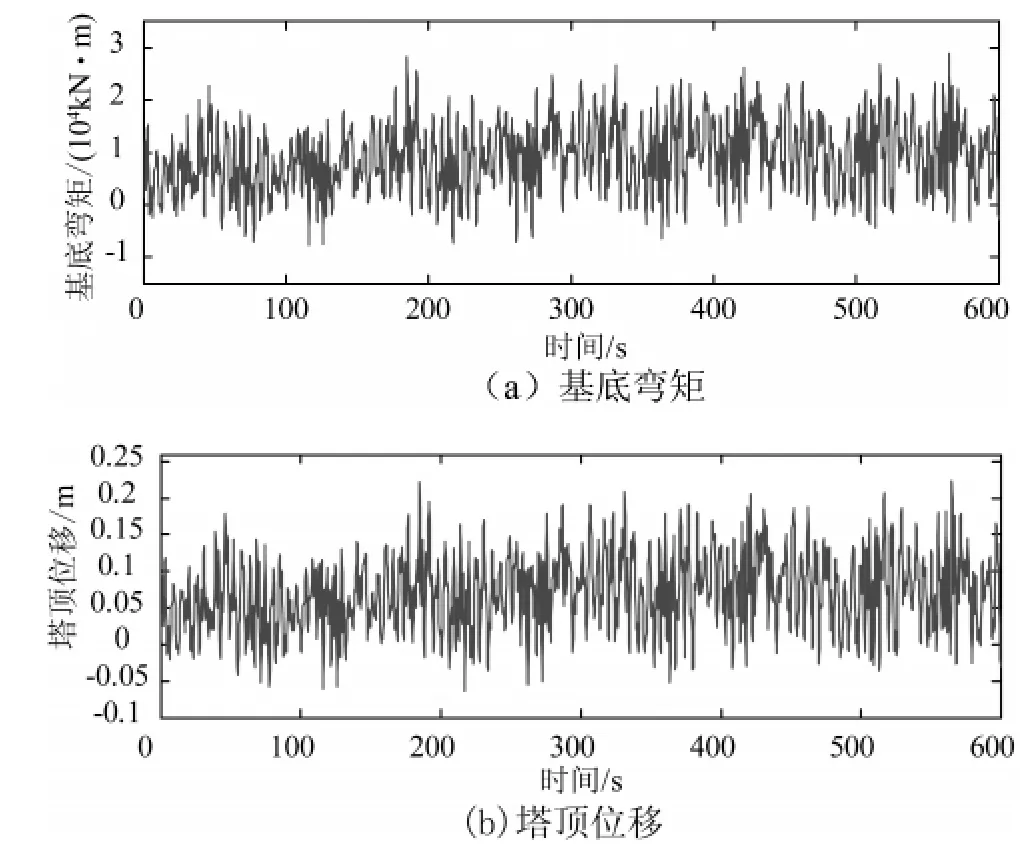
图9 钢筋混凝土风力发电塔基底弯矩与塔顶位移动力响应Fig.9 Tower base bending moment response and tower top displacement response of concrete wind turbine tower

钢筋混凝土风力发电塔基底弯矩动力响应如图9(a)所示，塔顶位移动力响应如图9(b)所示。由图9不难发现，基底弯矩最大值为29200 kN·m，塔顶位移最大值为0.221 m。显然，钢筋混凝土风力发电塔不存在“拍振”现象，结构动力响应偏小，这表明钢筋混凝土是一种更为理想的塔体材料。事实上，钢筋混凝土风力发电塔不仅存在结构动力响应较小的优势，而且具备造价便宜、无运输吊装限制(钢塔直径过大则难以找到适宜的运载工具)、无塔体厚度限制(钢塔厚度过大则难以实现弯曲成形)、耐腐蚀性强、减噪效果优良等特点［23］。因此，随着风力发电高塔系统不断向大型化、海洋化发展，不难预测钢筋混凝土风力发电塔的美好未来。

4.3 动力放大效应

为了比较风力发电高塔系统静力分析、动力响应分析两者之间的差异，本文基于相同的有限元模型进行了2种不同的分析:(1)将平均风压施加于风力发电高塔系统上，进行静力分析;(2)令随机Fourier谱模型、旋转Fourier谱模型中随机变量取均值，完成了风力发电高塔系统确定性动力响应分析。值得注意的是，上述2种情况都考虑了桨叶旋转效应。在进行静力分析时，考虑了桨叶旋转效应对平均风速的影响，但忽略了风速的脉动效应。严格来说，这已不再是静力分析，而应归于谐响应分析范畴(图4)。为了阐述方便，这里仍然称之为静力分析。在进行动力响应分析时，则同时考虑了桨叶旋转效应对平均风速和脉动风速的影响。2种情况下结构基底弯矩及塔顶位移比较见表2。

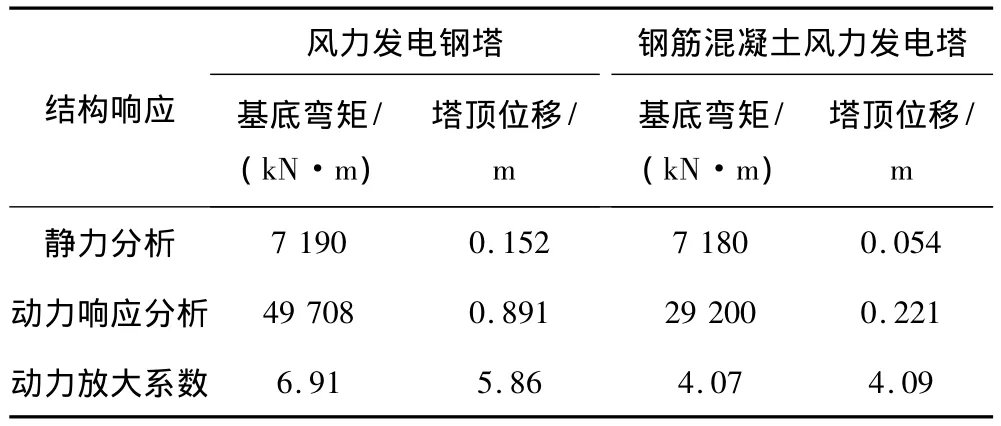
表2 风力发电高塔系统动力响应比较Tab.2 Dynamic response comparison between the steel wind turbine system＆the concrete one

定义结构确定性动力响应最大值与静力响应之比为动力放大系数。本例分析结果表明:风力发电钢塔的动力放大系数约为6.5，钢筋混凝土风力发电高塔的动力放大系数约为4，动力放大效应十分显著。因此，在设计过程中必须考虑动力放大效应，以结构动力响应分析结果为设计依据。风力发电高塔系统的动力放大系数偏大的主要原因在于:进行动力响应分析时不仅考虑了桨叶旋转效应对平均风速的影响，更为重要的是考虑了其对脉动风速的影响。

5 结论

(1)建立了风力发电高塔系统“桨叶－机舱－塔体－基础”一体化有限元分析模型。该模型不但能够考虑不同构件(尤其是桨叶与塔体)之间的耦合作用，而且能够反映结构应力集中、局部屈曲等细部特征，是一种精细化程度较高的结构模型。同时，对迄今还极为罕见的风力发电高塔系统塔体形式——钢筋混凝土风力发电塔进行了较为深入的探索。

(2)构建了风力发电高塔系统独特的风速场模型。基于随机过程的随机函数描述，考虑风速作用于旋转桨叶的物理机制，提出了旋转Fourier谱物理模型。旋转Fourier谱模型和随机Fourier谱模型分别适用于桨叶和塔体，依据随机函数法获得了各自的风速场，两者共同构建了风力发电高塔系统特有的风速场模型。

(3)实现了风力发电高塔系统风致动力响应分析。以随机Fourier谱和旋转Fourier谱为基础，结合“桨叶－机舱－塔体－基础”一体化有限元分析模型，完成了风力发电高钢塔和钢筋混凝土风力发电塔风致动力响应对比分析。研究表明，结构风致动力放大效应十分显著，故在设计过程中必须考虑该效应。相比较而言，风力发电钢塔存在明显的拍振现象，结构动力响应较大;而钢筋混凝土风力发电高塔不存在该现象，结构动力响应显著偏小，这表明钢筋混凝土是一种更为理想的塔体材料。依据随机函数法的基本思想可知，风力发电高塔系统确定性风致动力响应分析为后续的随机动力响应分析与抗风可靠度研究奠定了基础。

［1］全国风力机械标准化技术委员会.风力机械标准汇编［M］.北京:中国标准出版社，2006.

［2］汤炜梁，袁奇，韩中合.风力机塔筒抗台风设计［J］.太阳能学报，2008，29(4):422-427.

［3］Lobtiz D W.A Nastran-based computer program for structural dynamic analysis of horizontal axis wind turbine［R］.USA:Department of Energy，1995.

［4］ Murtagh P J，Basu B，Broderick B M.Along-wind response of a wind turbine tower with blade coupling subjected to rotationally sampled wind loading［J］.Engineering Structures，2005，27(8):1209-1219.

［5］Bazeos N，Hatzigeorgiou G D，Hondros I D，et al.Static，seismic and stability analyses of a prototype wind turbine steel tower［J］.Engineering Structures，2002，24(8):1015-1025.

［6］ Lavassas I，Nikolaidis G，Zervas P，et al.Analysis and design of theprototype of a steel 1-MW wind turbine tower［J］.Engineering Structures，2003，25(8):1097-1106.

［7］Kaminsky F C，Kirchhoff R H，Syu C Y，et al.A comparison of alternative approaches for the synthetic generation of a wind speed time series［J］.Journal of Solar Energy Engineering，1991，113(4):280-289.

［8］陈小波，陈健云，李静.海上风力发电塔脉动风速时程数值模拟［J］.中国电机工程学报，2008，28(32):111-116.

［9］ Powell D C，Connell J R.Verification of theoretically computed spectra for a point rotating in a vertical plane［J］.Solar Energy，1987，39(1):53-63.

［10］Connell J R.The spectrum of wind speed fluctuations encountered by a rotating blade of a wind energy conversion system［R］.USA:Batelle Pacific Northwest Laboratory，1982.

［11］Burton T，Sharpe D，Jenkins N，et al.Wind energy handbook［M］.Chichester:John Wiley ＆ Sons，2001.

［12］Veers P S.Three-dimensional wind simulation［R］.USA:Sandia National Laboratories，1988.

［13］ Hansen M O L.Aerodynamics of wind turbines［M］.Znd ed.London:Earthscan，2008.

［14］ Germanischer Lloyd.Rules and guidelines IV – industrial services，part 2:guideline for the certification of offshore wind turbines［S］.Hamburg:Germanischer Lloyd，2005.

［15］李杰，陈建兵.随机振动理论与应用新进展［M］.上海:同济大学出版社，2009:38-39.

［16］李杰，张琳琳.实测风速资料的随机Fourier谱研究［J］.振动工程学报，2007，20(1):66-72.

［17］艾晓秋.基于随机地震动模型的地下管线地震反应及抗震可靠度研究［D］.上海:同济大学，2005.

［18］ Dragt J B.The spectra of wind speed fluctuations met by a rotating blade，and resulting load fluctuations［R］.Netherlands:Energy research Center of Netherlands，1984.

［19］贺德馨.风工程与工业空气动力学［M］.北京:国防工业出版社，2006.

［20］Clough R W，Penzien J.Dynamics of structures［M］.New York:McGraw-Hill，1993.

［21］钟万勰.应用力学对偶体系［M］.北京:科学出版社，2002.

［22］钟万勰，林家浩.高层建筑振动的鞭梢效应［J］.振动与冲击，1985(2):1-6.

［23］贺广零.风力发电高塔系统风致随机动力响应分析与抗风可靠度研究［D］.上海:同济大学，2009.