微粒群优化理论在光电载荷安装误差修正中的应用*
2011-06-06田子希张国栋
田子希 黄 亮 杨 揆 刘 忠 张国栋
(海军工程大学电子工程学院 武汉 430033)
1 引言
利用空中机动单站搭载光电载荷对目标进行被动定位已经成为现代军事警戒探测系统的一种重要手段。结合空中机动单站的GPS位置信息和光电载荷对目标的角度测量信息,可以估计出目标的运动参数,实现对目标的定位解算。
随着美国政府SA(Selective Availability)政策的最终取消,GPS数据精度一般不超过10m,这对于中远距离(大于10km)定位的精度影响可以忽略。但光电载荷是通过螺丝与空中单站固连,安装过程由人员借助简单工具旋拧螺丝实现。由于缺少必要的对准检测设备,载荷的安装误差不易控制,从而会对载荷的定位性能产生较大影响。
传统的调整安装误差的方法一种是给定基准法[1~2],即在实验室环境条件下,借助专门的标校仪器,反复进行测试、调整,最终以提高安装精度。这种方法对环境要求高,实现复杂,费时费力。另一种则是基于扩展卡尔曼滤波等理论的滤波方法[3~4],这种方法可以在线估计,实时性好,但是对于未对准误差较大的情形则不适用,而且随着时间增加,线性化引起的误差导致修正误差增大,甚至发散。
微粒群优化(PSO)算法是在1995年由美国社会心理学家James Kennedy和电气工程师Russell Eberhart共同提出[5],基本思想源于他们早期对鸟类群体行为的研究。自微粒群算法提出以来,由于算法本身易实现,引起了国际上相关领域众多学者的关注和研究。在微粒群优化算法的应用方面,最早用于人工神经网络的训练,随后在函数优化、约束优化、极大极小问题、多目标优化等问题中均得到了成功的应用。
微粒群优化理论对状态方程、测量方程及系统噪声、测量噪声没有任何限制,因而其应用范围较广,这也是该理论区别于传统滤波算法的最大特点。因此,针对已有方法的不足,结合实际的应用背景,本文利用空中平台及合作目标(GPS位置信息已知的目标)的高精度GPS信息,引入微粒群优化理论来修正载荷的安装误差。
2 问题描述
由于光电载荷每次安装的实际环境不同,所产生的安装误差也不同;但因为载荷与平台间是通过螺钉刚性固定连接,所以对于同一次安装来讲,安装误差又可认为不变—因此,光电载荷安装误差仍属于系统误差的范畴,可以通过一定的方法抑制或消除。如图1所示,光电载荷测量值包括方位角β和俯仰角ε,其自身测角精度可达毫弧度。
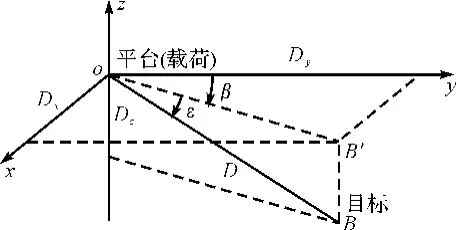
图1 光电载荷的测角原理
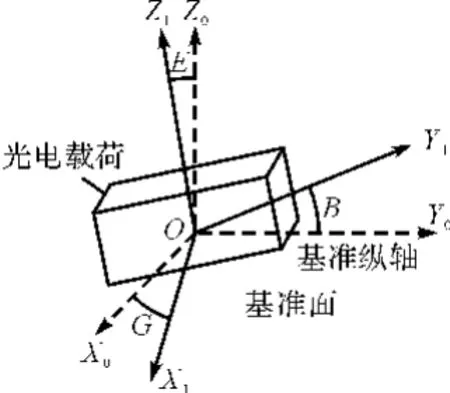
图2 光电载荷安装误差
光电载荷的高精度角度测量建立在测量基准精度较高的前提下,因此对于光电载荷是有严格的装配要求的,需要满足以下两点:1)载荷俯仰角测量基准,即载荷基准面与空中平台基准面平行;2)载荷方位角测量基准,即载荷方位零位应与空中平台艏向平行且方向一致。如图2所示,在理想情况下,光电载荷角度测量的基准坐标轴系OX1Y1Z1应与机动平台的坐标轴系OX0Y0Z0完全重合。但实际上不可能达到上述要求,总会存在一定的偏差,这个偏差就是安装误差,具体可分解为横滚安装误差G,俯仰安装误差E,偏航安装误差B。光电载荷的安装误差最大可达几度,将会对测角精度产生较大影响,从而影响到对目标的定位精度,必须加以消除。
3 微粒群优化理论在误差修正中的应用
载荷安装误差修正本质上属于非线性优化问题。为了可靠解决优化问题,人们试图离开解析确定型优化算法,转而探讨对函数解析性质要求较低甚至不作要求的随机型优化方法。最早的随机型优化方法是基于Monte Carlo方法随机搜索算法,真正有效且具有普遍适应性的优化方法是近十多年来人们模拟自然界的一些自然现象而发展起来的一系列仿生型智能优化算法,如模拟退火方法、进化类算法、群体智能算法等。
微粒群优化算法[6~8]是一种进化计算技术,将优化问题的每一个可能解视为搜索空间中的一个“微粒”,根据对环境的适应度将群体中的个体(微粒)移动到好的区域。所有微粒都有一个由优化函数所决定的适应值。这些微粒在搜索空间中根据自身及同伴的飞行经验以一定的速度飞行,追随当前的最优微粒,最终达到全空间最优解。微粒群优化算法的最大优势在于简单、容易实现,并且没有许多参数的调节。

结合本文应用背景,利用微粒群优化算法进行载荷安装误差修正的具体过程为:
1)随机初始化每一个微粒。
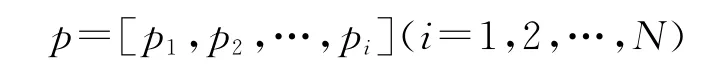
每个微粒拥有位置(此处具体是指待求的横滚误差、俯仰误差、偏航误差)、速度、适应度等属性,可以通过一个多维向量来表示。为防止粒子越界,初始化微粒的位置和速度时限定一个范围:
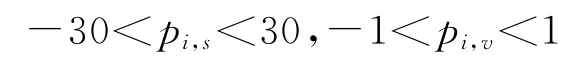
pi,s使微粒保持运动惯性,能够拓展搜索空间,可以探索新的区域,其上限则决定了当前位置与最好位置间的区域分辨率。若上限太高,微粒可能会飞过最好解,若太小,则又不能保证微粒足够的区域,导致陷入局部最优值。其中,β′i、ε′i由角度测量值结合空中机动单站的姿态信息以及待求的载荷安装误差经坐标转换而来。
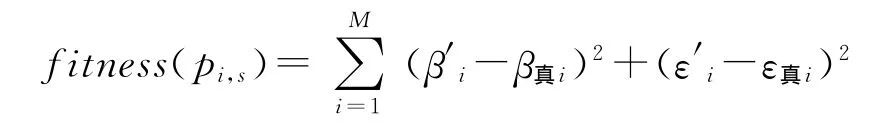
3)计算每个微粒的局部最优位置pi,s和全局最优位置G。

4)更新微粒的速度和位置。
微粒群优化的速度及位置更新公式分别为:
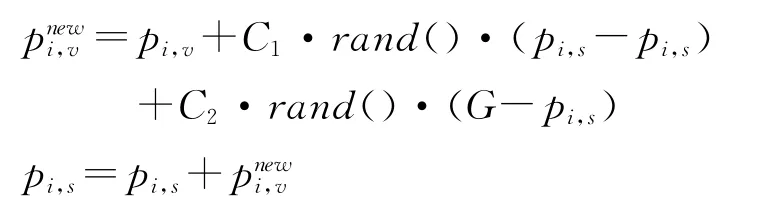
微粒通过不断调整自己的位置来搜索新的解。微粒在进化过程中还记忆一个个体最优解,记录该微粒经过的最优位置和适应度值;而整个微粒群存在一个全局最优解,表示整个微粒群的最优位置和最佳适应度。当两个最优解都找到后,在每次迭代中,每个微粒通过跟踪两个极值来更新自己速度和位置,即自己搜索到的最优解及群体搜索到的最优解。
5)将微粒适应值与经过的最优位置pi,s作比较,若较好,则将其作为当前的最优位置pi,s;对全局最优位置G也作相同的比较。在3)中计算了pi,s和G,这一步则更新了pi,s和G。
6)判断是否达到结束条件,若是则转7),否则转2)。
与其它进化算法一样,微粒群算法中最常用的终止准则是预先设定一个最大的飞行代数,或者是当搜索过程中解的适应度在连续多少代后不再发生明显改进时,终止算法。
7)得到最优解p*。
2)评价微粒的适应度。
适应度是唯一能够反映并引导优化过程不断进行的参量,所解决的问题不同,适应度评价函数也不同。在求解载荷安装误差的实际问题中,优化目标就是使得转换后的角度测量值与角度真实值达到最佳拟合,因此采用如下评价函数:
4 仿真分析
假定目标初始位置:东经121.7947°、北纬29.7650°、高程0m,以速度5m/s、航向60°运动。空中机动平台的初始位置为:东经121.9111°、北纬29.7546°、高程3000m,以速度20m/s、航向240°运动。系统角度量测噪声1.8°,速度量测噪声为0.5m/s。先后将光电载荷三个轴向的安装误差设定为小误差条件(横滚、俯仰、偏航安装误差分别为1°、0.9°、-1°)、大误差条件(横滚、俯仰、偏航安装误差分别为-6°、7°、5°)。利用 Matlab产生仿真数据。
在具体解算时,微粒群算法的相关参数设置分别为:微粒群的规模POPSIZE=20,算法执行的最大代数MN=5000,惯性系数W=1.0、认知参数C1=1.8、社会参数C2=1.8。仿真结果见图3、图4。
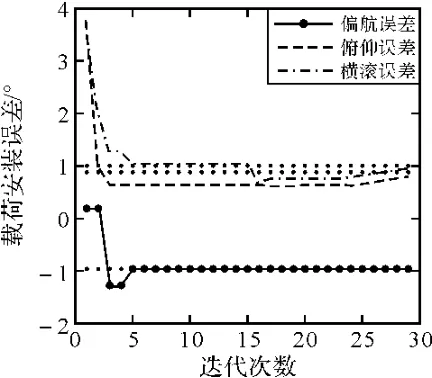
图3 偏航误差=-1、横滚误差=1、俯仰误差=0.9
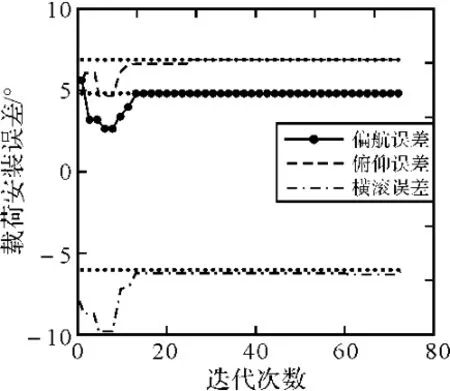
图4 偏航误差=5、横滚误差=6、俯仰误差=7
在小误差条件下,进行10次蒙特卡洛仿真后的平均收敛代数为5,而且偏航、俯仰、横滚误差的均方差分别是0.05°、0.09°、0.07°。
在大误差条件下,进行10次蒙特卡洛仿真后的平均收敛代数为14,偏航、俯仰、横滚安装误差的均方差分别是0.06°、0.06°、0.10°。
由仿真结果可以看出,不论是小误差还是大误差条件下,算法都能够收敛到正确的安装误差结果,且相对估计误差均不超过5%,具有较高的估计精度。
5 结语
微粒群优化算法通过大量微粒群在一定搜索空间从不同位置同时找出问题解,从而能够动态调整当前局部和全局位置,运算简单、易于实现,只需很少的代码和参数。在分析空中机动平台光电载荷安装误差原理的基础上,本文采用微粒群算法来优化求解,仿真结果证实了方法的可行性,从而为安装误差的修正提供了一种新思路。随着现代高速DSP技术的发展,微粒群算法也有望进入实际工程应用。
[1]许自富,阮安路,张颿,等.无人机机载传感器现场校准系统的设计[J].仪器仪表学报,2007,28(8):28~41
[2]刘诗斌.无人机磁航向测量的自动罗差补偿研究[J].航空学报,2007,28(2):8~15
[3]Crassidis J L,Markley F L.Unscented filtering for spacecraft attitude estimation[J].Journal of Guidance,Control and Dynamics,2003,26(4):536~542
[4]潘平俊,冯新喜,赵晓明.机动目标模型研究与发展综述[J].指挥控制与仿真,2006,28(3):12~15
[5]Chen Yaobin,Hu Xiaohui,Eberhart R.Cognitive models for learning to control dynamic systems[C]//Proc IEEE International Conference on Neural Networks,2008
[6]Eberhart R,Kenndy J.A new optimizier using particle swarm theory[C]//Proc of the 6th International Sym-posium on Micro Machine and Human Science.New York:IEEE,1995:39~43
[7]邓林义,林焰.粒子群算法求解任务可拆分项目调度问题[J].控制与决策,2008,23(6):682~683
[8]Shi Y,Eberhart R.Parameter selection in particle swarm optimization[C]//Proc of the 7th Annual Conf on Evolutionary Programming.New York,1998:591~600
[9]伊文天.方位角的GPS测量方法[J].测绘与空间地理信息,2008,2(31):120~122
[10]黄亮,刘忠,李剑辉,等.空中机动平台光电载荷无源定位算法及坐标变换分析[J].海军工程大学学报,2009(6):35~38
