不同去旋角度进气共转盘腔内流动与换热研究

杨守辉，王锁芳

（南京航空航天大学能源与动力学院，南京 210016）

不同去旋角度进气共转盘腔内流动与换热研究

杨守辉，王锁芳

（南京航空航天大学能源与动力学院，南京 210016）

以带有去旋喷嘴的共转盘腔为研究对象，运用RNG k-ε湍流模型，分别对3种喷嘴角度（90°、60°、30°）的3维模型进行了数值计算，揭示了去旋角度对盘腔内气体切向速度、盘腔内压降和转盘表面换热的影响规律。研究结果表明：随着去旋角度的减小，盘腔内气体的切向速度减小，盘腔内压降减小，转盘表面的局部努赛尔数Nur增大。

共转盘腔；去旋角度；流动；数值计算；航空发动机

0 引言

航空发动机涡轮前温度不断提高，使得涡轮部件工作环境进一步恶化，发动机的可靠性降低和寿命缩短，因此要对涡轮中的高温部件进行冷却。目前，大多采用从压气机引气的冷却方式。在实际发动机中，冷气主要由压气机盘腔径向内流引出，但由于旋转效应气体流过盘腔时会受到径向哥式力的阻碍，造成很大的压力损失，从而降低了发动机的效率。为减小旋转效应，抑制气流受到的哥式力，在共转盘腔中应用了去旋喷嘴。

针对带去旋喷嘴的共转盘腔内气体的流动与换热特性，许多学者对盘腔的结构参数和流动参数的影响进行了研究。Owen等[1-2]通过求解边界层内的动量方程，对外围屏上带有去旋喷嘴的共转盘腔内的压降值进行了理论分析，并对理论模型进行了试验研究，发现理论分析与试验符合得很好；黄爱霞针对外围屏上带有去旋系统的共转盘腔进行了数值计算，揭示了冷气流量、湍流参数等因素对盘腔内流动换热的影响[3]。

本文就去旋喷嘴的去旋角度等参数对共转盘腔内的流动与换热的影响进行了数值研究，以期更好地了解盘腔内气流切向速度、压降和盘面努赛尔数等参数的变化规律。

1 计算模型及数值方法

1.1 几何条件

径向进气的共转盘腔如图1所示。盘腔以角速度Ω绕中心轴旋转，气流由外围屏上的去旋喷嘴流入，由盘腔底部流出。记盘腔半径为b，定义去旋喷嘴的轴线与旋转切线之间的夹角为去旋角度θ。在盘腔外围屏上均匀布置18个直径为8mm的去旋喷嘴，在无量纲冷气流量CW=2.6×103的情况下，分别对θ=90°、60°、30°的模型进行了计算。

1.2 控制方程

连续方程

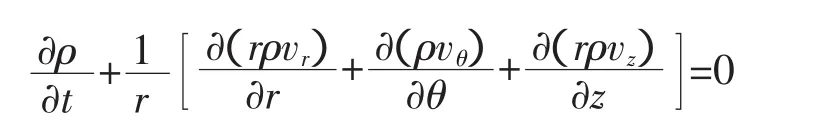
运动方程

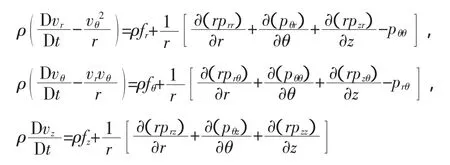
能量方程

1.3 网格划分

因为涡轮盘腔具有轴对称性，并且外围屏上的去旋喷嘴是以20°的角度均匀布置的，所以盘腔内的流动结构是周期性的，在此取盘腔的1/18区域进行网格划分。计算域只包括流体域，不包括2转盘及外围屏的固体域。为满足2转盘表面Ekman边界层的特点，在距离盘面0.1mm处布置第1层网格，以1.1的增长比例共布置6层，计算盘腔网格如图2所示。经过网格无关解试验，选择网格数在30万左右。

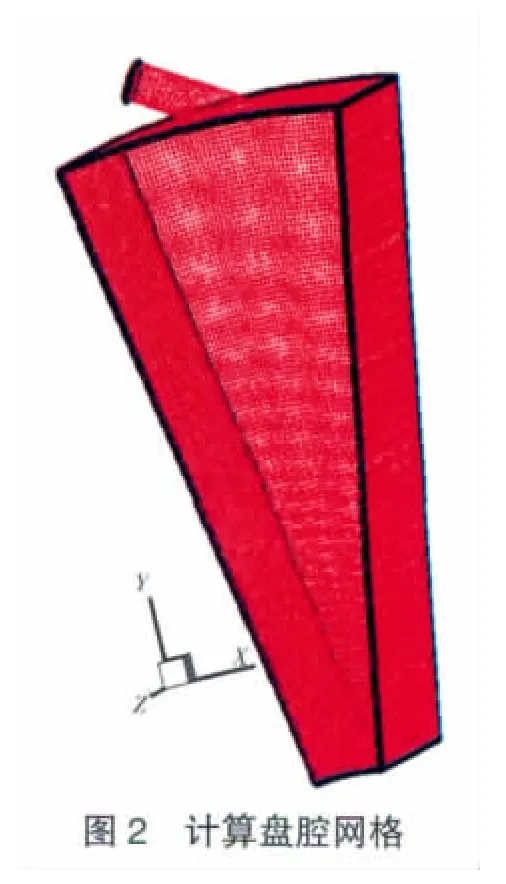
1.4 计算设置及边界条件

应用RNG k-ε湍流模型进行计算，压力速度耦合采用SIMPLE算法，近壁面采用标准壁面函数，2阶迎风格式离散化。连续方程、动量方程、流体体积函数方程收敛判据为迭代残差小于10-3，能量方程收敛判据为迭代残差小于10-6。

边界条件设置如下：入口采用质量入口边界条件；出口采用压力出口；外围屏及左侧壁面为绝热；右侧壁面为恒温，T=400K；所有固壁面均采用无滑移边界条件。旋转雷诺数 Reφ=ρΩb2/μ，ρ为流体密度，无量纲质量流量CW=m/μb，μ为气体的黏度。

2 计算结果与分析

2.1 计算方法验证

为验证本文计算方法的正确性，首先对文献[4]中径向进气的共转盘腔模型进行了数值计算，针对文献中模型 A，在 CW=-946、Reφ=6×105和 CW=-309、Reφ=6×105条件下，计算得到的盘腔内气体无量纲切向速度VΩ=VΦ/Ωr，沿盘腔无量纲半径r/b的分布如图3所示。可以发现计算结果与Firouzian M等人的试验结果相符较好。

2.2 盘腔内的流动

Y-Z截面流线如图4所示。从图中可见，共转盘腔内的气体流动具有典型的源—汇结构，流动结构分成了4种类型区域：源区（source region）、埃克曼边界层区（Ekman）、汇区（sink layer）和核心区（interior core），这与文献[4]中的理论分析相符。从X-Y截面流线图中可见，由于受旋转效应影响，盘腔内的流体具有与盘腔旋转方向相同的切向速度VΦ，而阻碍冷气径向内流的哥式力正是由VΦ产生的。去旋效应就是利用冷气由去旋喷嘴进入盘腔时产生的切向速度分量UΦ来抵消VΦ，从而减小由此而产生的径向哥式力，最终达到降低盘腔内压力损失的目的。

在Reφ=0.23×106时，气流由不同θ的喷嘴进入盘腔处的速度三角形和速度矢量如图5所示。图中：w为冷气的相对速度；Ωb为盘腔旋转产生的牵连速度；U为冷气由喷嘴进入盘腔处的绝对速度。由速度合成公式可知，UΦ=Ωb-wcos θ，其中-wcos θ是由喷嘴的去旋效应产生的切向速度分量。定义盘腔进口处旋流比β＝（Ωb-wcos θ）/Ωb，可见 β 成为衡量去旋效应的重要参数，当β＜1时,喷嘴具有去旋效应，且β越小去旋效应越强。

从图5中可见：

（1）当 θ=90°时，wcos θ=0、UΦ=Ωb，所以总有 β=1，即喷嘴无去旋效应。但从θ=90°的矢量图中可知，由喷嘴进入盘腔气体的UΦ小于盘腔内气体的VΦ，由于受入流气体惯性力的影响，使VΦ在一定程度上减小。

（2）当 θ＜90°时，总有 β＜1。从图 5（b）中可见，进入盘腔气流的UΦ与腔内气流的VΦ方向相反，使得在喷嘴附近的腔内气体出现明显的折返回流，在图 5（c）中由于受喷嘴的去旋效应影响，VΦ甚至反向。

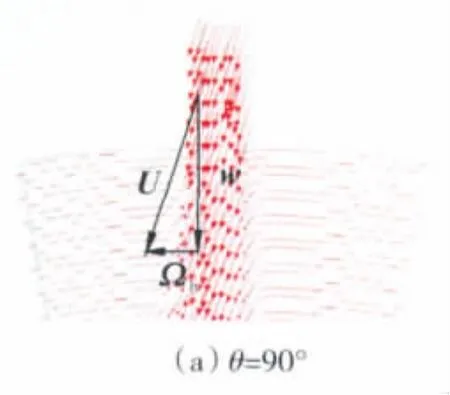
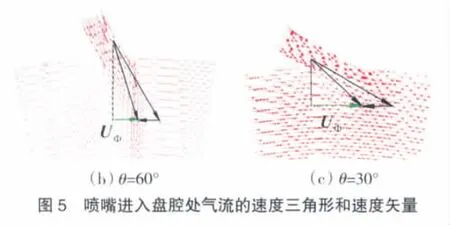
（3）分析速度合成公式 UΦ=Ωb-wcos θ，在旋转角速度Ω一定时，随着θ的减小，wcos θ增大，去旋效应增强。比较图 5 中相同 Reφ下，θ=90°、θ=60°和 θ=30°时的矢量图可知 UΦ，θ=30＜UΦ，θ=60＜UΦ，θ=90，可见 θ=30°的去旋效应大于θ=60°的，即去旋角度越小，β越小，与上面的分析相符。

在 Reφ=0.23×106时，VΩ随 θ的变化如图 6 所示。从图中可见，在 θ=90°时的 VΩ最大，在 θ=60°时的 VΩ次之；而在 θ=30°时的 VΩ最小。在 θ=90°时，低半径处腔内气流的切向速度达到当地盘面速度的3倍，产生很大的径向哥式力；在 θ=30°时，在 r/b=0.8 处 VΩ=0，此处盘腔内气体受到的去旋效应与旋转效应相当，出现“驻点”，在 r/b＞0.8 位置 VΩ＜0，去旋效应开始强于旋转效应，这是因为随着θ的减小，UΦ降低，对VΩ的抵消作用增强，使得VΩ减小。而且，随着r/b的减小VΩ增加，这是由于：（1）在低半径处气流通过盘腔的截面积减小，在流量一定时，低半径处气体的相对径向速度增大，由哥式力公式FC=-2mΩu可知，气体受到的切向哥式力增大，使VΩ增大；（2）盘腔内旋转气流的角动量守恒，因此随半径减小旋转速度增大。

虽然去旋喷嘴能够降低VΩ，但带有去旋喷嘴的盘腔内VΩ依然是随半径的减小而增大，在高半径处VΩ甚至出现负值，但在低半径处VΩ还是很大，这是由于去旋喷嘴在高半径的盘缘处，去旋进气惯性力对高半径处的VΩ影响较大，而对低半径处的VΩ抵消作用较小，为使盘腔内的VΩ整体减小，需对去旋系统进行改进。

2.3 盘腔内的压降

当θ时不同CP随Reφ的变化如图7所示。从图中可见，θ越小，无量纲压降CP越小，根据图6分析的结果，θ越小去旋效应越强，盘腔内的气体VΩ越小，气体受到的径向哥式力变小，则气体通过盘腔时的阻力减小，从而使盘腔内的无量纲压降CP减小。

当θ一定时，随着Reφ的增大，盘腔内气体的无量纲压降CP增大，这是由于随着Reφ的增大，旋转效应增强，腔内气体的Vφ增大，使气体受到的径向哥式力增大，阻碍了腔内气体的流动，使CP增大。并且随着Reφ的增大，气体受到的离心力增大，也使CP增大。由上面的分析可知，去旋喷嘴的应用确实能够减小气体流过共转盘腔时的总压损失，但也使盘腔结构变得复杂，盘腔系统质量增加。

2.4 加热盘表面换热

在Reφ=2.8×106时Nur随θ的变化如图8所示。从图中可见，随着θ的减小，加热盘表面的局部努赛尔数Nur逐渐变大，这是因为随着θ的减小，去旋效应增强，使得腔内气体与盘表面的相对速度变大，热边界层变薄，从而使盘表面换热能力增强。随着气体向低半径处流动，温度逐渐升高，换热能力减弱，Nur减小。在r/b=0.8位置附近Nur达到最大值，而在0.95

3 结论

（1）在Reφ一定时，随着θ的减小，旋流比减小，盘腔内气体的VΩ减小，去旋效应增强。

（2）在 0.6×106

（3）加热盘表面的平均努赛尔数Nur随θ的减小而增大，换热能力加强。在r/b=0.8附近，Nur达到最大值；在0.95

[1]Farthing P R,Chew J W,Owen J M.The use of de-swirl nozzles to reduce the pressure drop in a rotating cavity with radial inflow[R].ASME 89-GT-184.

[2]Farthing P R,Owen J M.De-swirled radial inflow in a rotating cavity [J].International Journal of Heat and Fluid Flow,1991,12（1）:63-70.

[3]黄爱霞，王锁芳.反旋进气盘腔内流动与换热的数值研究[J].航空动力学报，2008，23（9）：1684-1688.

[4]Firouzian M,Owen J M,Rogers R H.Flow and heat transfer in a rotating cavity with a radial inflow of fluid.Part 2:Velocity,pressure and heat transfer measurements[J].International Journal of Heat and Fluid Flow,1986,7（1）:21-27.

[5]曹玉璋，陶智，徐国强，等.航空发动机传热学[M].北京：航空航天大学出版社，2005：226-265.

[6]吕品，王成明，赵熙，等.温度分布对自由盘层流换热的影响[J].航空发动机，2010,36（4）：8-11.

Investigation on Flow and Heat Transfer inside Co-rotating Disc Cavity with Different De-swirl Angle

YANG Shou-hui,WANG Suo-fang
（College of Energy and Power Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China）

The 3D numerical simulation of the co-rotating disc cavity with the deswirl nozzles was carried by the RNG k-ε turbulence model with three kinds of de-swirl angles （90°,60°,and 30°）.The influence of the de-swirl angle on the tangential velocity,the pressure loss in the disc cavity and the heat transfer of the rotational disc is discoverd.The results show that as the de-swirl angle reduces,the flow tangential velocity in the disc cavity decreases,the pressure loss in the disc cavity reduces,the local Nurnumber of the rotational disc surface increases.

co-rotating cavity;de-swirl angle;flow;numerical calculation;aeroengine

杨守辉（1985），男，在读硕士研究生，主要从事流动与换热研究。