五轮铰接式移动机器人的重构特性及分析

徐贺，伏虎，张振宇，谭大伟，武永见，薛开，栾钰琨

(哈尔滨工程大学 机电工程学院，黑龙江 哈尔滨 150001)

对于面向多种移动导航任务的机器人，要求对不同负载和地型都具有一定的适应性.例如Nano Rover采用关节角式可变结构的底盘，Nomad采用可放缩底盘，行星探险机器人SMC采用了主从可重构结构［1-3］.由此可知，可重构多机动模式、具有分离式被动差分机构连接三厢车体的微小轮式机器人具有适应崎岖地面的特点.在差速机构的轴上连接一个可转向的复合轮(第五轮)，这种悬挂系具有结构简单、适应多任务需求的特点，既保留了四轮式机器人的特性，又提供了附加的驱动力及滑转测量能力.

机器人多重构参数与性能指标非线性关系的影响分析可以采用偏导方法，但较复杂.该类问题属于多元函数的可视化问题，常规做法是进行降维处理［4］.也有采用将多维函数进行超平面范数链化转为三维函数显示的方法［5］，还有平行坐标法［6］等.

本文针对一个具有三箱体五轮分离式差分机构的可重构机器人，采用iSGIHT-FD软件，利用Approximation方法中的响应面模型(response surface method，RSM)逼近局部特性，对优化后数据结果进行可视化(VDD)敏度分析，获得了多个重构变量对非线性性能指标量化影响的相对大小，并用实验给予验证.

1 移动机器人的扩展重构构型

图1 可重构移动机器人的构型以及第五轮的重构Fig.1 Prototypes of reconfigurable robot and the 5th wheel

表1 移动机器人构型参数值Table 1 Value of parameters of mobile robot prototype

机器人重构的过程中应满足以下条件:机器人相对于自身几何中心对称，车体水平.通过改变底盘长度与高度、4个轮子的前后倾角α与内外倾角β、主轮轮径、主轮宽度、第五轮摇杆长度来重组成不同构型，使机器人稳定性、几何通过性均可调节以满足不同任务的需求.机器人重构构型如图1所示，其特性如表1所示.

2 机器人多变量与性能指标

对机器人进行空间解析建模任意时刻可重构移动机器人的空间解析模型见图2.{L}表示世界坐标系;参考点R固定在差分器两输入轴连线与主车体纵向铅垂平面的交点上，点D1、D2分别是两侧摇臂机构与差分器两输轴的理论交点，坐标系{D1}、{D2}分别固定在对应的摇臂机构上;坐标系{H1}、{H2}、{H3}、{H4}与各自主轮转向机构固连;坐标系{E1}、{E2}与相应摇臂机构固接;点 A1、A2、A3和A4固定于相对应的轮子上.

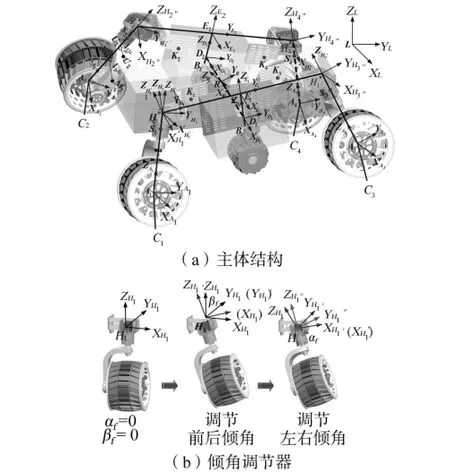
图2 可重构移动机器人空间解析模型Fig.2 Spatial analytical model of reconfigurable robot

轮 1 ～ 4 的前后、内外倾角分别是:αf、βf、αf、-βf、αb、βb、αb、- βb.规定重构时，先绕铰接点的 Y轴旋转β，再绕新坐标系的X轴旋转α.各摇臂倾角以及底盘长度、高度的调节如图3所示.

采用9个独立设计参数，重构变量为

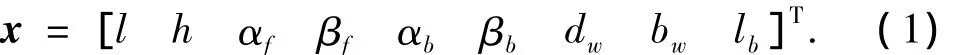
移动机器人在崎岖地面上受到多种阻力(压实阻力、推土阻力、滚动阻力和重力阻力)，而轮子的形状、尺寸及机器人的轴距、轮距和整机质量等都与这些阻力有着非线性的关系.纵向对称构型优化的3个分目标函数分别要求机器人的整机质量mRobot最轻、静态稳定性最大(静态稳定裕角ΦRobot最小)和轮子阻力矩 TRobot最小.即［7］

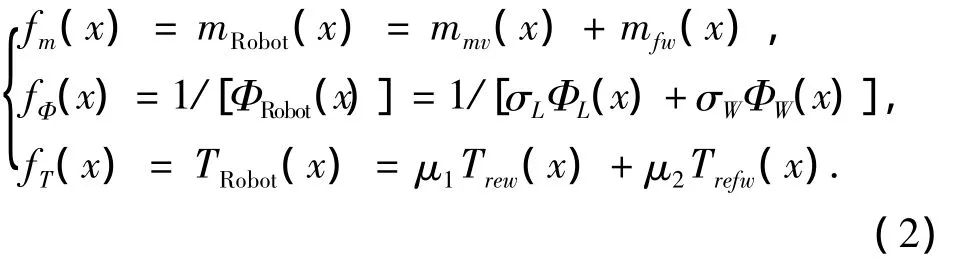
式中:μ1是主轮机构阻力矩比例系数，0≤μ1≤1;μ2是第五轮机构阻力矩比例系数 0≤μ2≤1，μ1+μ2=1.

线性约束为

式中:HC0表示机器人许用净高，m;nmL表示主体机构纵向稳定性安全系数;nL、nw表示机器人纵向稳定性安全系数;Wmax表示最大扭矩，N·m;［τ］表示铝合金7075的许用剪应力，MPa;Wt表示轮毂外环抗扭截面模量，m3;Tmax、Mmax表示最大扭矩和最大弯矩，N·m;［σ］表示7075的许用正应力，MPa;Wz=0.5Wt，表示轮毂外环抗弯截面模量，m3;G表示7075的剪切模量，MPa;Ip=πD4(1-α4)/32，表示截面极惯性矩，m4;［φ］表示7075单位长度扭转角的许用值，(°)/m;［p］，pw表示许用接地压力和接地压力，kPa.

将目标函数集成于(用MATLAB的M函数文件)iSIGHT-FD软件中，如图4所示，选用邻域培植遗传算法(NCGA)，得到 Pareto最优解集［8］，从而获得优化构型参数.

3 机器人构型的多变量影响分析

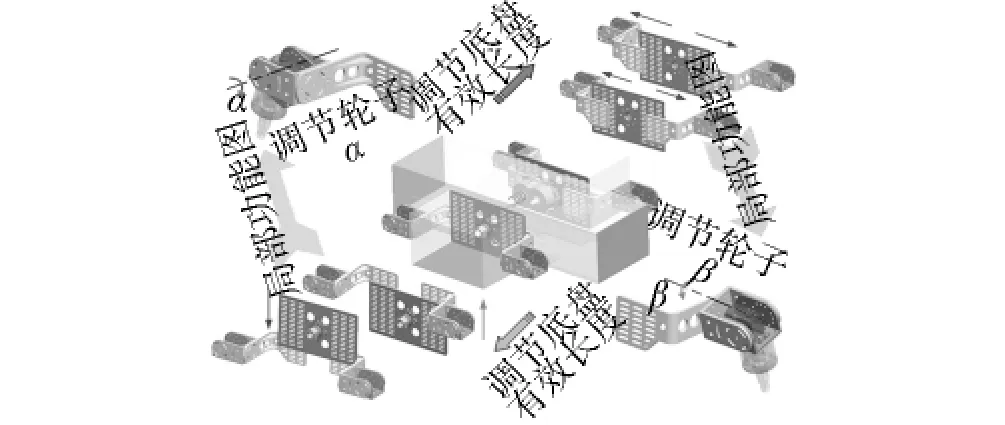
图3 底盘悬挂系统结构Fig.3 Structure of chassis suspension system

图4 iSIGHT-FD软件的Approximation图形界面Fig.4 Approximation GUI of iSIGHT-FD

在获得Pareto最优解集后，对数据结果采用Approximation方法中的RSM逼近局部特性，这样避免了高强度仿真计算，减少迭代时间，平滑设计空间的数值噪声，预估输入输出参数之间的响应关系.四阶响应面模型如下:

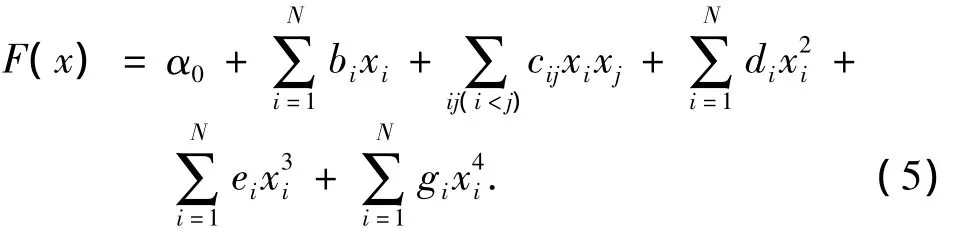
式中:a0、bi、cij、di、ei、gi为拟合系数，xi为变量.

四阶响应面模型需调用［(N+1)(N+2)/2］+2N次精确计算，可以在优化过程中通过使用动态文件的方式不断将新的设计点添加到文件中，自动更新近似模型.初始化时使用的样本点不保证都在拟合出来的响应面上.本算法可有效避免局部最优解.图5、6所示分别为近似模型方法和可视化敏度分析的界面.

由于稳定性指标是非线性的，用传统优化算法很难得出各变量对稳定性的影响.因此，本文通过VDD进行敏度分析，对各滑动条进行设定式拖拽，获得各变量对稳定性指标的量化影响的相对大小.如图6所示.

最终获得的重构变量(设计变量)的优化值为:

xopt=［0.385 0.001 -84.36 -12 89.24-9.63 0.149 6 0.111 4 0.121 2］T纵向对称构型目标函数的优化值为

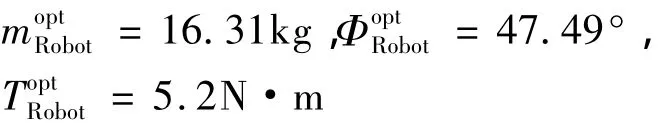
优化的可重构移动机器人纵向对称构型如图7所示.机器人该构型下具有较小的质量、较好的稳定性和较低的轮子阻力矩.

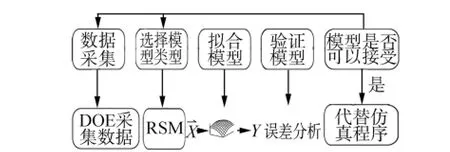
图5 近似模型方法流程Fig.5 Flow chart of approximation

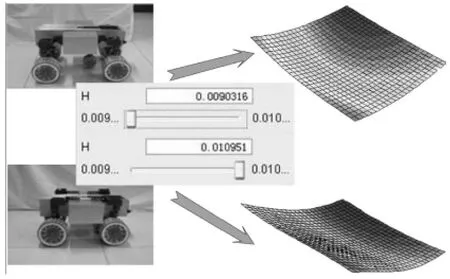
图6 可视化敏度分析Fig.6 Sensitivity analysis of the VDD

图7 对称优化构型中的可倾覆构型Fig.7 Overturnable prototype from symmetrical optimized prototype

结合图8分析可知:机器人质量随主轮宽度和直径的增大而上升，而与各轮臂倾角以及底盘长度、底盘长度无关.阻力矩与质量变化有关，而与其他参量无关;在讨论主轮直径与宽度对主轮机构惯性力推土阻力、压实阻力滚动阻力和重力阻力影响时，已得推土阻力和压实阻力随主轮直径增大而下降，但主轮惯性力、滚动阻力和重力阻力随主轮直径增大而上升且起主要作用，最终导致当主轮直径与宽度同时增大时，阻力矩呈现上升趋势.

结合图9分析可知:稳定性与各轮轮臂倾角、底盘长度、净高、主轮直径、宽度、第五轮连杆长度有关.α和底盘高度对稳定性影响较大，稳定性随α负向增加、底盘高度减小而增大，主轮直径次之，β和主轮宽度对前后轮影响程度相近，居第3位，底盘有效长度和第五轮轮臂长度对ΦRobot影响较小，居第4位.

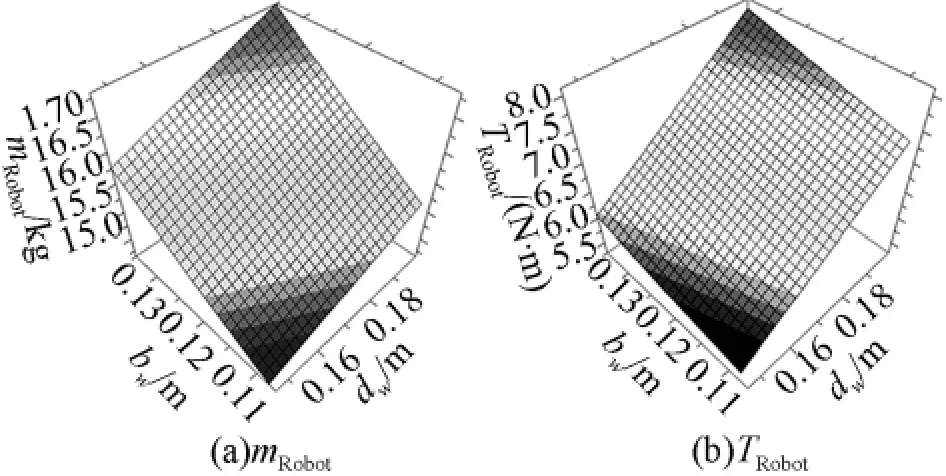
图8 MRobot和TRobot与dw和bw的关系Fig.8 The relation of MRobot，TRobot，dwand bw

4 重构实验

表2和图10分别为典型构型的理论值与实际值对比表和相应的样机构型图.

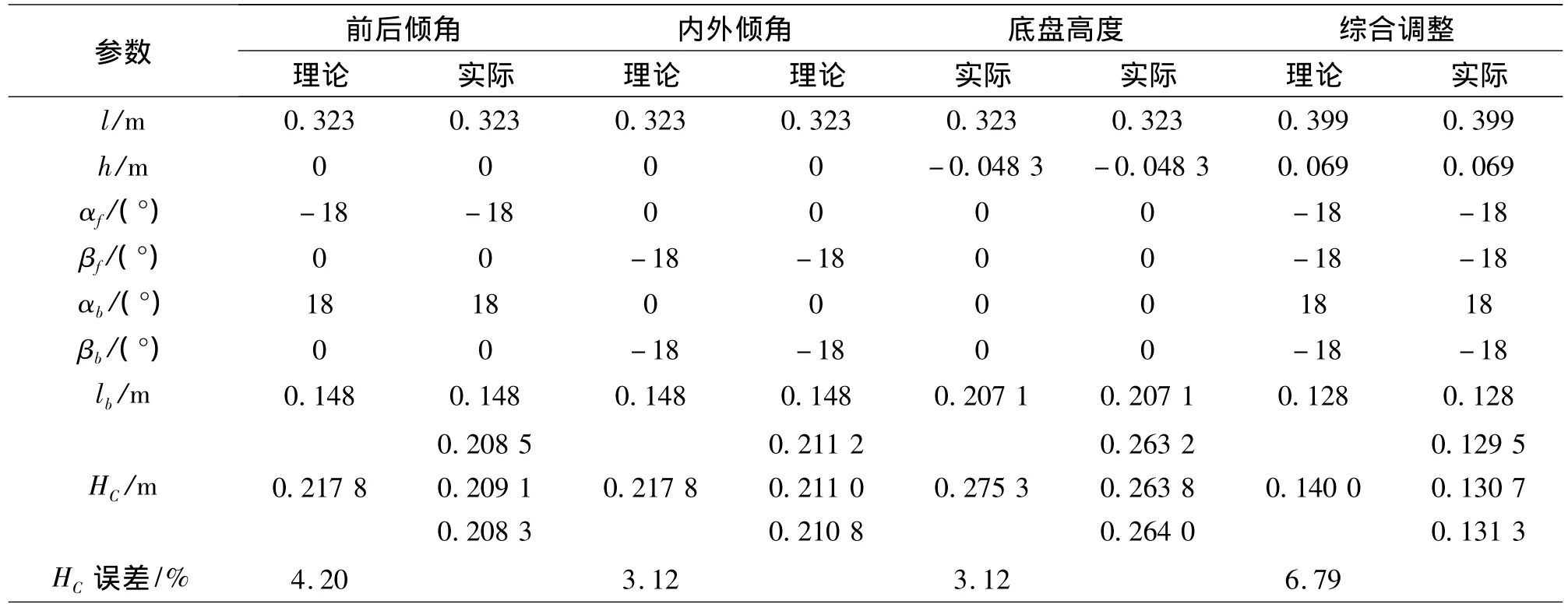
表2 对称典型构型的理论值与实际值对比Table 2 Comparison of theoretical and experimental value of symmetrical prototype

图10 对称构型测试Fig.10 Test of symmetrical prototype

对机器人常规构型使用精度为±1mm钢尺测得 Le=0.334 3m，We=0.333 5m，HC=0.214 8m.而理论值 Le=0.323m，We=0.330m，HC=0.227m.分别调节 α、β 角，净高误差为4.20%和3.12%.可见确有一定误差，但该误差对机器人相应功能影响很小，在可接受范围内.

5 结束语

运用多目标优化的方法可使可重构机器人获得对应约束条件下的具有较小质量、较好稳定性和较低轮子阻力矩的重构构型.采用Approximation方法中的四阶响应面模型对各个重构变量分析，可知:机器人质量随主轮直径和宽度的增加而增加;轮子阻力矩随主轮直径和宽度增加而增加;前、后轮前后倾角和底盘高度对机器人稳定性影响最大，主轮直径次之，前后轮内外倾角以及主轮宽度居第3位，第五轮摇杆长度、底盘有效长度的影响居末位.机器人对称构型的主要功能参数的理论值和实验值的对比的最大误差不超过6.79%，在可接受范围内，表明响应面模型的有效性.

［1］WILCOX B H.Nanorover technology and MUSESCN mission［C］//4th Proceedings of International Symposium on Artificial Intelligence，Robotics and Automation in Space(i-SAIRAS’97).Tokyo:National Academy Press，1997:6-28.

［2］ROLLINS E，LUNTZ J，FOESSEL A，et al.Nomad:a demonstration of the transforming chassis［C］//Proceedings of 1998 IEEE International conference on Robotics＆Automation.Leuven:National Press，1998:1-89.

［3］KAWAKAMI A，TORII A，MOTOMURA K，et al.SMC rover:planetary rover with transformable wheels［C］//Proceedings of the 41st SICE Annual Conference.Osaka:National Press，2002:10-67.

［4］XU G，YAMAZAKI K，CHENG G D.A new two-point approximation approach for structural optimization［J］.Struct Multidisc Optim，2000，20(1):22-28.

［5］邓扬晨，钱卫，张卫红，等.一种多元函数的可视化方法［J］.飞机设计，2002，12(4):26-29.

DENG Yangchen，QIAN Wei，ZHANG WEI hong，et al.A kind of visualization method in expressing multivariable function［J］.Aircraft Design，2002，12(4):26-29.

［6］YUAN Xiaoru，CHEN Baoquan.HDR VolVis:high dynamic range，volume visualization［C］//IEEE Transactions on Visualization and ComputerGraphics.Research Triangle Park.NC，USA，2006:433-445.

［7］XU He，TAN Dawei.Configuration design of a novel mobile robot with 5th wheel［J］.Key Engineering Materials，2010(419-420):605-608.

［8］HUBAND S，HINGSTON P，BARONE L，et al.A review of multiobjective test problems and a scalable test problem toolkit［J］.IEEE Trans on Evolutionary Computation，2006，10(5):477-506.

［9］TAN K C，GOH C K，MAMUN A A，et al.An evolutionary artificial immune system for multi-objective optimization［J］.European Journal of Operational Research，2008，187(2)，371-392.