镍基单晶合金板裂纹尖端塑性区分析

杨丽红，吴林志，曲嘉

(1.哈尔滨工程大学航天与建筑工程学院，黑龙江 哈尔滨 150001;2.哈尔滨工业大学 复合材料研究所，黑龙江 哈尔滨150001)

镍基单晶高温合金具有优良的高温抗疲劳、抗蠕变性能，是目前制造先进航空发动机和燃气轮机叶片的主要材料.为了满足高性能航空发动机的设计需求，多年来，各国十分重视镍基单晶高温合金的开发和研究，取得了一系列有意义的研究成果.研究人员对镍基单晶合金的力学性能、本构描述等在理论上和实验上都进行了大量研究，但相对而言，对镍基单晶合金的断裂问题研究不多.材料裂纹问题是力学领域的一个研究热点，温志勋等［1］通过实验和有限元法研究了镍基单晶合金裂纹扩展路径，结果表明，环境温度对裂纹启裂和扩展以及断裂强度和断裂形式有较大影响.N.Marchal［2］采用弹粘塑性模型对循环蠕变加载下的镍基单晶裂纹尖端应力应变场进行了分析，结果表明，裂纹尖端变形是沿着特定矢量方向的.于金江等［3］研究了Re对单晶合金的拉伸断裂的影响.

在外加应力作用下，裂纹尖端附近的材料会发生屈服，说明裂纹前缘存在塑性区.裂纹尖端塑性区的形状和尺寸是分析裂纹的重要参数，裂纹的扩展与裂尖塑性区有着密切关系.关于裂纹尖端塑性区的研究，比较典型的方法是从宏观断裂力学角度，按照适当的屈服准则确定塑性区的大小及形状.高鑫等［4］采用宏观断裂力学理论对正交各向异性单向复合材料中斜裂纹尖端塑性区进行了分析，结果表明，裂纹倾角对裂尖塑性区范围和形状有明显影响.

在进行正交各向异性材料弹塑性分析时，可以采用Hill屈服准则、Hoffman屈服准则和Tsai-Wu屈服准则等.其中，Hill屈服准则因简单实用而被广泛采用.Liu C［5］研究了Hill屈服准则在拉压性能不同材料中的应用，结果表明，在小应变情况下，可以采用Hill屈服准则描述拉压性能不同材料的屈服特性.丁智平等［6］通过在Hill屈服准则表达式中增加一个四次修正项，提出了一个考虑拉-剪耦合的屈服准则，通过对材料屈服应力的预测说明考虑拉-剪耦合的意义.本文应用Hill屈服准则和一种修正的Hill屈服准则，分别在平面应力和平面应变状态下，对镍基单晶合金板裂纹尖端塑性区进行分析.

1 屈服准则

1.1 Hill屈服准则

Hill将Mises屈服准则推广到正交各向异性材料中，给出正交各向异性材料屈服准则

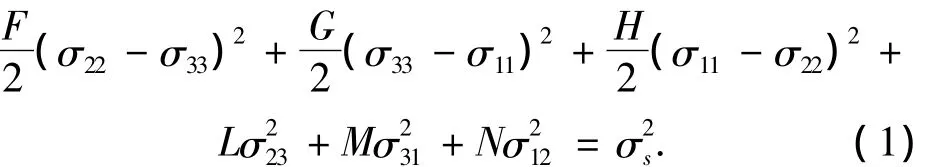
式中:σij(i，j=1，2，3)为材料主坐标系下应力，F、G、H、L、M、N为相互独立的材料参数，可由单向拉(压)实验和纯剪切实验确定，σs为参考屈服应力，可取材料某一主轴方向的屈服应力.

对于镍基单晶合金材料，忽略其包氏效应，且认为其在3 个晶轴方向［100］，［010］，［001］具有相同的力学性能，于是Hill屈服准则变为

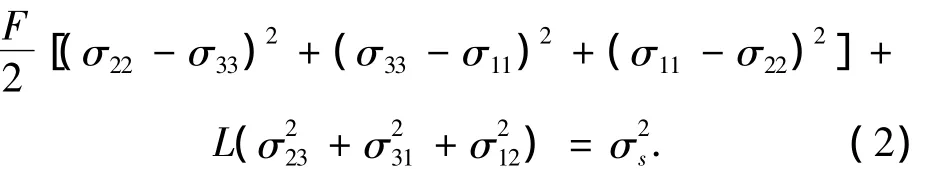
文献［7］给出实验得到的镍基单晶合金DD3的材料参数，见表1.

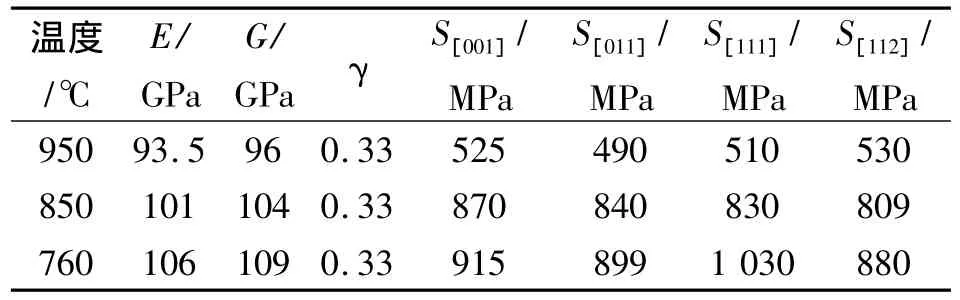
表1 DD3镍基单晶合金材料特性Table 1 Properties of DD3 nickel-based single crystal

根据实验测得的［001］、［111］取向屈服应力S［001］、S［111］，可以算得材料参数 F、L，见表 2［6］.

在平面应力状态下，σ33=σ13=σ23=0，Hill屈服准则变为

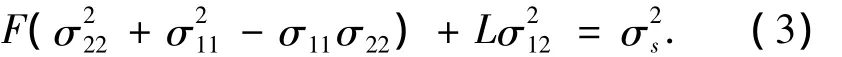
在平面应变状态下，σ33=γ(σ11+σ22)，σ13=σ23=0，γ为材料主轴方向的泊松比.于是Hill屈服准则变为

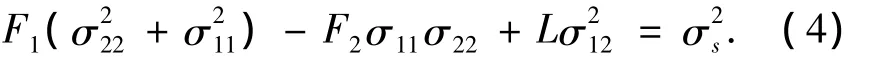
式中:F1=F(1-γ+γ2)，F2=F(1+2γ-2γ2).

1.2 考虑拉-剪耦合的修正Hill屈服准则

Hill屈服准则没有考虑正交各向异性材料偏轴方向存在的拉-剪耦合，在描述单晶材料屈服特性时精度不高.本文通过在Hill屈服准则表达式中增加一个二次修正项，给出如下形式的镍基单晶合金屈服准则:

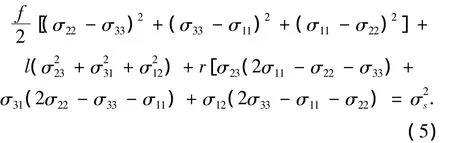
设沿［001］取向拉伸时，拉伸应力等于［001］取向屈服应力 S［001］，于是得 f=1.为了精确，根据实验测得的多个晶体取向屈服应力［7］，采用最小二乘法拟合材料参数l、r，结果见表2.

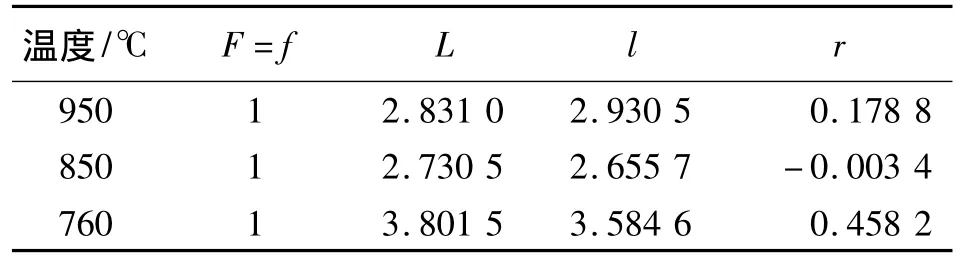
表2 镍基单晶合金材料参数Table 2 Material parameters of nickel-based single crystal

将拟合得到的材料参数f、l、r代入修正Hill屈服准则式(5)，对镍基单晶合金的屈服应力进行预测，所得结果见表3.在［001］取向，预测的结果应与实验结果相同.表3中同时给出由Hill屈服准则预测的镍基单晶合金屈服应力［6］.显然，在［001］、［111］取向预测的屈服应力应与实验结果相同.

从表3中可以看出，采用本文的修正Hill屈服准则预测镍基单晶合金的屈服应力，与采用Hill屈服准则相比，能够降低预测误差，提高预测精度.

在平面应力状态下，式(5)变为

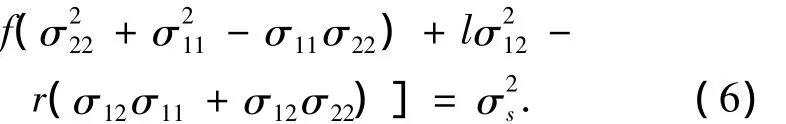
在平面应变状态下，式(5)变为

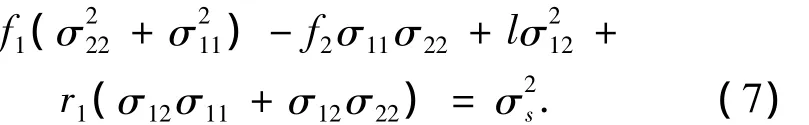
式中:f1=f(1-γ+γ2)，f2=f(1+2γ-2γ2)，r1=r(2γ -1).

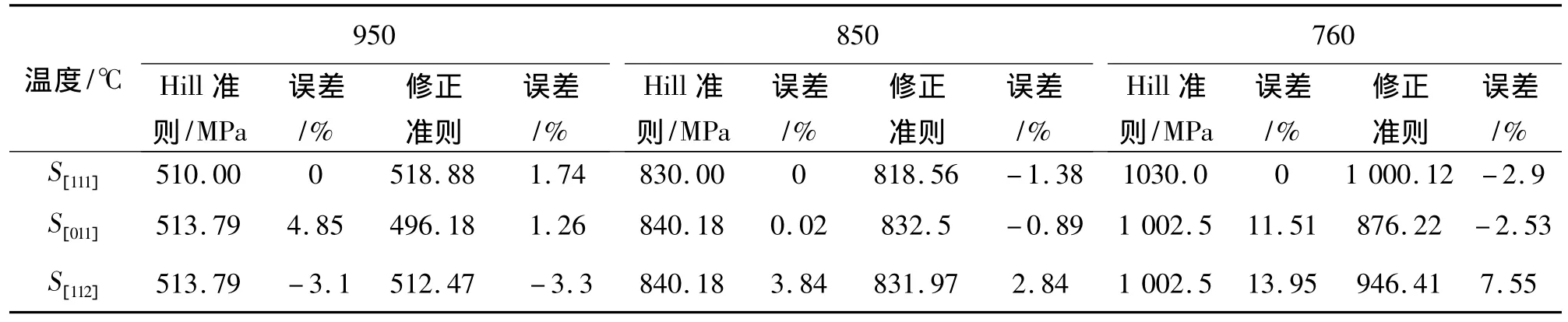
表3 由屈服准则预测的镍基单晶合金屈服应力Table 3 Yield stress of nickel-based single crystal forecasted by yield criteria

2 镍基单晶板裂纹尖端塑性区

2.1 裂纹尖端应力场

无限大镍基单晶合金平板上中心穿透裂纹如图1所示.设裂纹沿材料晶轴方向，长度为2a.

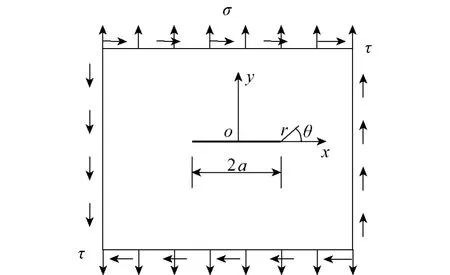
图1 镍基单晶合金板Ⅰ、Ⅱ复合型裂纹Fig.1 Mixed modeⅠ，Ⅱcrack of nickel-based single crystal plate

取坐标轴与材料弹性主轴重合，则正交各向异性材料的柔度矩阵为

对于镍基单晶合金，有

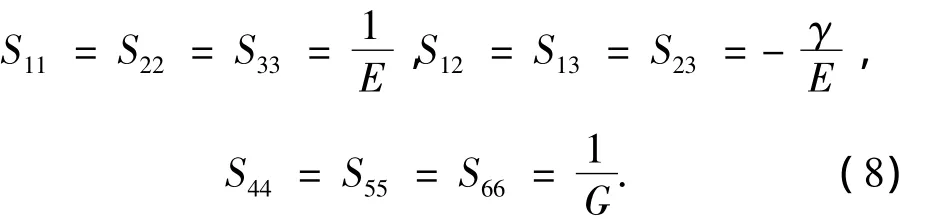
式中:E、G、γ分别为材料晶轴方向的拉压弹性模量，剪切弹性模量和泊松比.

此时镍基单晶合金板平面问题的特征方程为

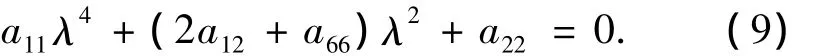
在平面应力状态下，有a11=a22=S11，a66=S66，a12=S12;在平面应变状态下，有a11=a22=(1-γ2)S11，a66=S66，a12=(1+ γ)S12.

文献［7］给出了正交各向异性材料板Ⅰ、Ⅱ复合型裂纹尖端应力场如下:

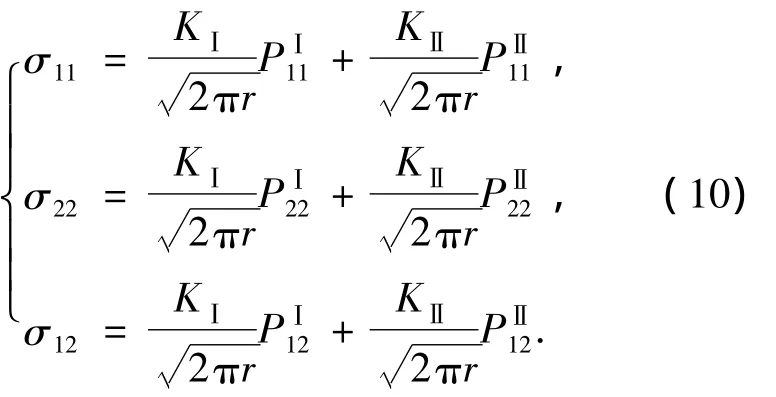
式中:KⅠ、KⅡ分别为Ⅰ、Ⅱ型裂纹应力强度因子.

式中:λ1、λ2为方程(9)的根.

2.2 裂纹尖端塑性区

对应Hill屈服准则，将式(10)代人式(3)，得镍基单晶合金板穿透裂纹在平面应力状态下的塑性区计算式:

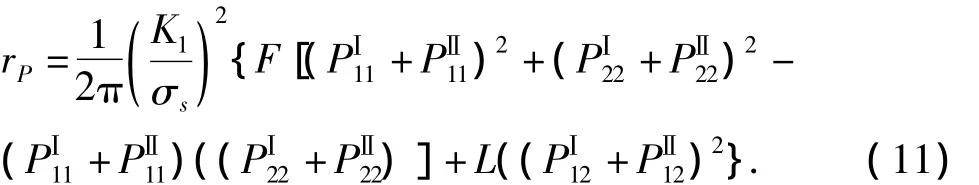
将式(10)代人式(4)，得平面应变状态下的塑性区计算式:

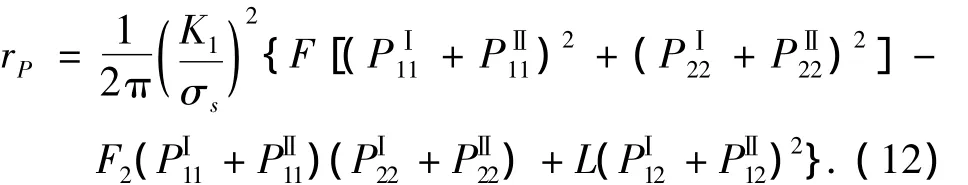
对应考虑拉-剪耦合的修正Hill屈服准则，将式(10)代人式(6)，得镍基单晶合金板穿透裂纹在平面应力状态下的塑性区计算式为

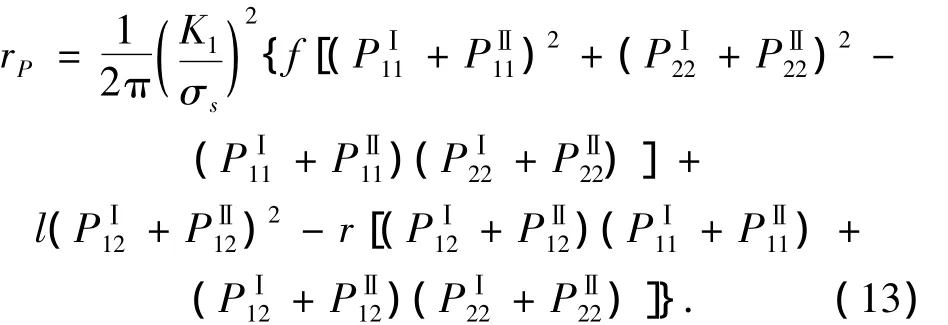
将式(10)代人式(7)，得在平面应变状态下的塑性区计算式为

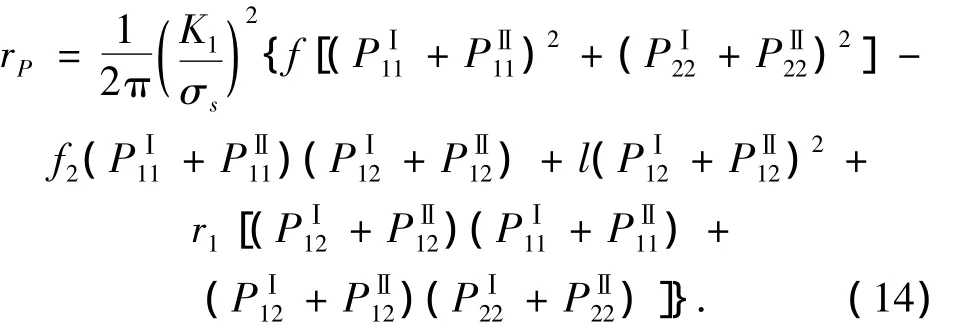
3 结果分析

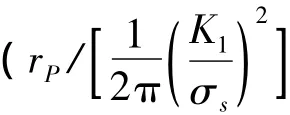
由图2可以看出，裂纹尖端塑性区关于裂纹面对称分布.在平面应变状态下，镍基单晶合金裂纹尖端塑性区的范围明显大于均质材料的塑性区范围;平面应力状态裂尖塑性区大于平面应变状态裂尖塑性区.

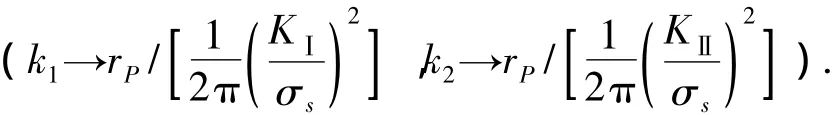
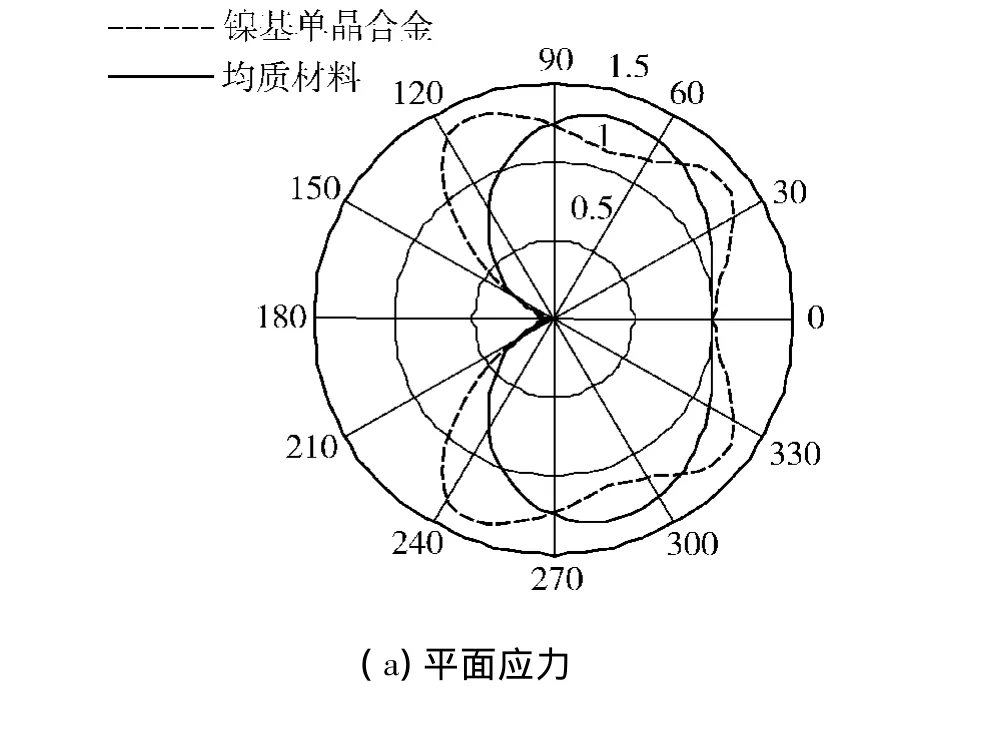
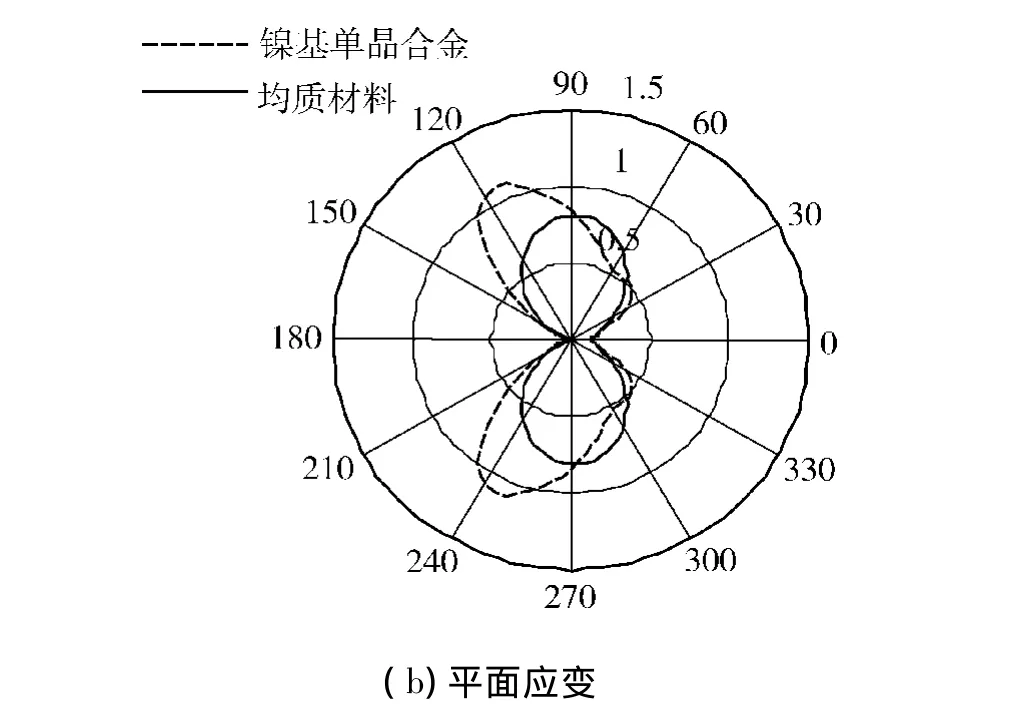
图2 Ⅰ型裂纹尖端塑性区Fig.2 Mode I crack tip plastic zone

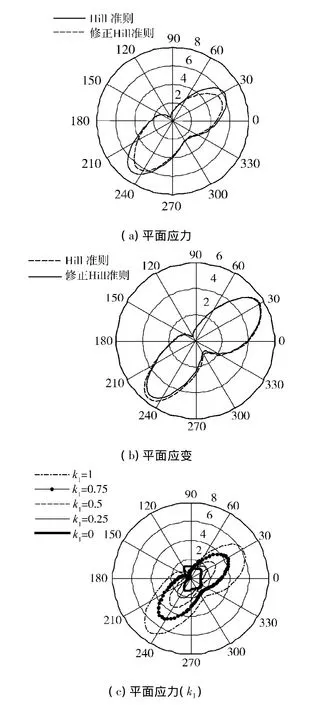
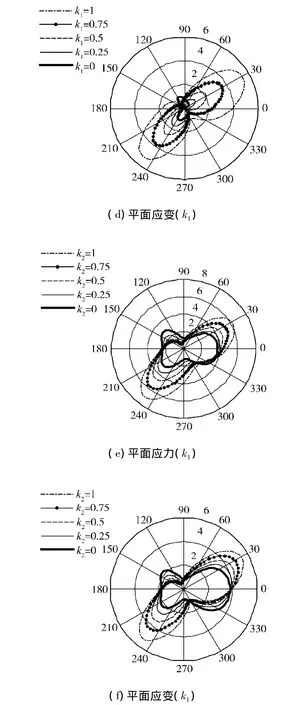
图3 镍基单晶合金Ⅰ、Ⅱ复合型裂纹尖端塑性区Fig.3 Mixed modeⅠ，Ⅱ crack tip plastic zone of nickel-based single crystal

由图3(a)、(b)可以看出，在760℃时，当考虑拉—剪耦合，在平面应力状态下，裂纹尖端塑性区减小，在平面应变状态下，裂纹尖端塑性区增大.本文也对850℃和950℃时的裂纹尖端塑性区进行了分析，发现在这2种温度下，拉剪耦合对裂纹尖端塑性区基本不产生影响.由图3(c)～(f)可以看出，在平面应力状态下，镍基单晶合金裂纹尖端塑性区尺寸随复合比的递增速度大于平面应变状态下的递增速度;塑性区尺寸随复合比k1的递增速度大于随k2的递增速度.

基于Hill屈服准则，求得k=1时不同温度下镍基单晶合金Ⅰ、Ⅱ复合型裂纹尖端塑性区如图4所示.作图时3种温度下的参考屈服应力均取915 MPa.由图4可以看出，温度对镍基单晶合金裂尖塑性区的尺寸影响较大.

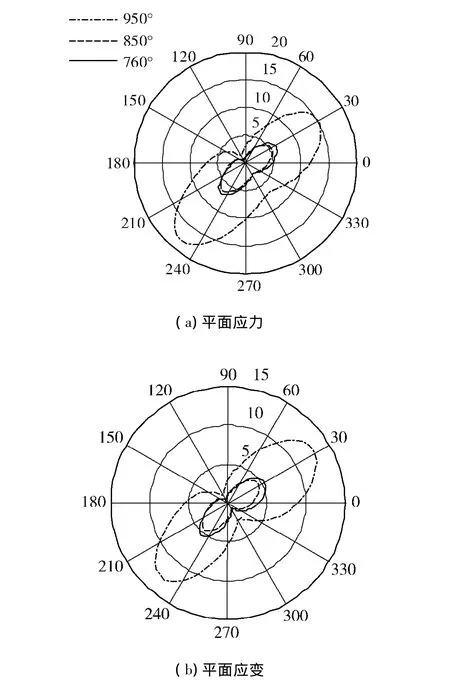
图4 不同温度下基单晶合金Ⅰ、Ⅱ复合型裂纹尖端塑性区Fig.4 Mixed modeⅠ，Ⅱcrack tip plastic zone of nickel-based single crystal for different temperatures

4 结束语

文章通过对Hill屈服准则进行修正，构造一考虑拉-剪耦合的修正Hill屈服准则.用构造的修正准则对镍基单晶合金的屈服应力进行预测，与Hill屈服准则的预测结果比较，预测精度提高.在平面应力和平面应变状态下，分别基于Hill屈服准则和本文的修正Hill屈服准则，推导了镍基单晶合金I、II复合型裂纹尖端塑性区的计算表达式.拉-剪耦合在760℃时对镍基单晶合金板裂纹尖端塑性区尺寸有影响，而在850℃和950℃时，对裂纹尖端塑性区尺寸基本没有影响;在平面应力状态下，镍基单晶合金板裂纹尖端塑性区尺寸随复合型裂纹复合比的递增速度大于平面应变状态下的递增速度;温度对镍基单晶合金板裂尖塑性区的尺寸有影响.950℃时塑性区尺寸远大于其他两低温情况的塑性区尺寸.

［1］温志勋，苟文选，岳珠峰.镍基单晶裂纹扩展路径研究［J］.稀有金属材料与工程，2007，36(9):1549-1553.

WEN Zhixun，GOU Wenxuan，YUE Zhufeng.Crack propagation paths and fracture of Ni-based single crystal［J］.Rare Metal Materials and Engineering，2007，36(9):1549-1553.

［2］MARCHAL N，FLOURIOT S，FORESR S，et al.Crack-tip stress-strain fields in single crystal nickel-base superalloys at high temperature under cyclic loading［J］.Computational Materials Science，2006，37(1):42.

［3］于金江，候桂臣.一种含Re单晶高温合金的拉伸断裂行为［J］.稀有金属材料与工程，2006，35(8):1231-1234.

YU Jinjiang，HOU Guichen.Tensile and fracture behavior of a single crystal superalloy containing Re［J］.Rare Metal Materials and Engineering，2006，35(8):1231-1234.

［4］高鑫，康兴无，王汉功.正交各向异性单向复合材料裂纹尖端塑性区求解［J］.固体火箭技术，2009，32(5):554-559.

GAO Xin，KANG Xinwu，WANG Hangong.Solution to the crack tip plastic zone of orthotropic unidirectional composites［J］.Journal of Solid Rocket Technology，2009，32(5):554-559.

［5］LIU C，HUANG Y，STOUT M G.On the asymmetric yield surface of plastically orthotropic materials:a phenomenological study［J］.Acta Mater，1997，45(6):2397-2406.

［6］丁智平，刘义伦，尹泽勇，等.镍基单晶合金弹塑性本构模型［J］.航空动力学报，2004，19(6):755-760.

DING Zhiping，LIU Yilun，YIN Zeyong，et al.Study of elastic-plastic constitutive model for single crystal nickelbased superalloy［J］.Journal of Aerospace Power，2004，19(6):755-760.

［7］张少琴.复合材料断裂分析的特殊方法［M］.北京:兵器工业出版社，2003:37-55.

［8］中国航空材料手册编委会.中国航空材料手册:第二卷［M］.2版.北京:中国标准出版社，2002:36-41.