RBF网络自整定PID控制在网络化控制系统中的应用

葛锁良， 杨旭玮， 张亚东

（合肥工业大学 电气与自动化工程学院，安徽 合肥 230009）

随着计算机网络的广泛应用和网络技术的不断发展，控制系统的结构正在发生变化。与传统的点对点控制系统相比，网络化控制系统具有共享信息资源、减少系统布线、易于扩展和维护等优点。目前网络控制已经成功地应用于国民经济和国防建设的各个领域，如车辆控制［1－2］、电力生产、远程医疗［3］和远程教学。

由于网络的介入，不可避免地使信息存在时延、丢包等问题，从而造成系统性能恶化，甚至导致系统的不稳定［4］。其中网络诱导时延是影响系统性能的最重要的因素。传统PID控制器的参数需要根据被控对象的数学模型来调整，而控制过程中的滞后性、控制参数的高阶性增加了对控制参数的调整难度［5］。

本文将RBF神经网络和传统PID控制器有机结合起来，利用RBF神经网络的自学习、自适应能力对PID控制器参数进行在线整定，实现网络化控制系统的优化控制，其效果优于传统PID控制器。

1 网络化控制系统

网络化控制系统（Network Control Systems，简称NCS）是指某区域内传感器、控制器、执行器和通信网络的集合，使该区域内不同地点的用户实现资源共享和协调操作，是一种全分布式、网络化的闭环实时反馈系统［6－7］。网络化控制系统由被控对象、传感器、执行器、控制器和计算机网络5部分组成，其结构简图如图1所示。由于网络带宽有限且网络中的数据流量变化不规则，当多个节点通过网络交换数据时，常常出现数据碰撞、网络拥塞等现象，因而不可避免地出现信息交换时间延迟，这种由网络引起的时间延迟称为网络诱导时延（Network－induced Delay）。

图1 网络化控制系统结构

网络诱导时延主要包括：

（1）传感器到控制器之间的时延，从传感器采样得到某个数据的时刻起至该数据开始被控制器处理的这段时间。

（2）控制器的计算时延，从控制器开始计算到计算完成产生控制信号的这段时间。

（3）控制器到执行器之间的时延，控制器产生某控制信号的时刻起至该信号被执行器接收的这段时间。

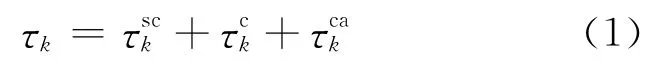
这样，网络化控制系统的时延为：控制器的计算时延τck与τsck、τcak相比，它的数值和变化都很小，常可忽略，即

由于时延出现在控制回路中，并且随负载变化呈现不确定性，使原本等间隔的数字采样变得不再等间隔，造成反馈和控制信号产生随机的滞后，使系统的超调增大、调节时间变长，且当时延增大到一定程度时，可能导致系统不稳定。

2 RBF神经网络自整定PID控制器

径向基函数（Radial Basis Function，简称RBF）神经网络是由Moody和Darken于20世纪80年代末提出的一种神经网络。它是一种3层单向传播的前馈网络，能以任意精度逼近任意连续函数，且运算量小［8－10］，收敛速度快。

2.1 RBFNN自整定PID控制系统的结构

RBF神经网络自整定PID控制器由PID控制器和RBF神经网络2部分组成。该控制器主要通过RBF神经网络的自学习能力在线辨识得到系统近似模型，进而获得被控对象的Jacobian信息，实现对PID参数的在线调整。其原理框图如图2所示。

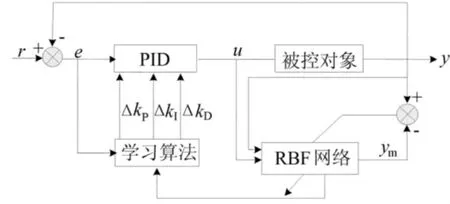
图2 RBF网络自整定PID控制器的原理框图

2.2 RBF神经网络

RBF网络是由输入层、隐含层和输出层组成。从输入层到隐含层的变换函数的映射是非线性的，从隐含层到输出层的映射是线性的，可通过调整权系数来改变网络的输出，从而加快学习速度，避免局部极小值的问题［11－12］。其拓扑结构如图3所示。

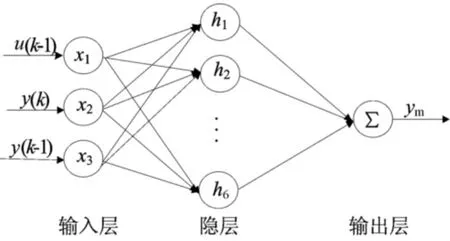
图3 RBF神经网络拓扑结构

其中，X＝［u（k－1），y（k），y（k－1）］T是网络的输入向量。RBF网络的径向基向量H＝［h1，h2，…，h6］T，其中hj为高斯基函数，即

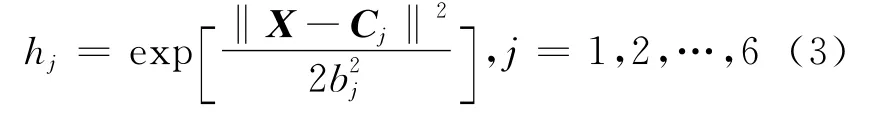
其中，网络的第j个节点的中心向量为Cj＝［cj1，cj2，cj3］T，j＝1，2，…，6；bj为隐层节点j的基宽参数，且为大于零的数。RBF网络输入层到隐含层的权值为1，网络隐含层到输出层的权向量为W＝［w1，w2，…，w6］T。RBF网络的输出为：

RBF网络学习的性能指标为：

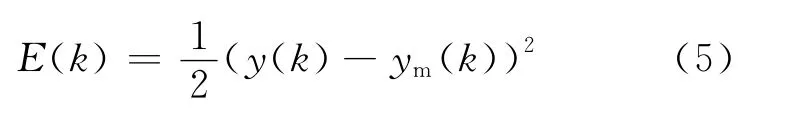
根据梯度下降法，输出权、节点基宽参数及节点中心矢量的迭代算法如下：

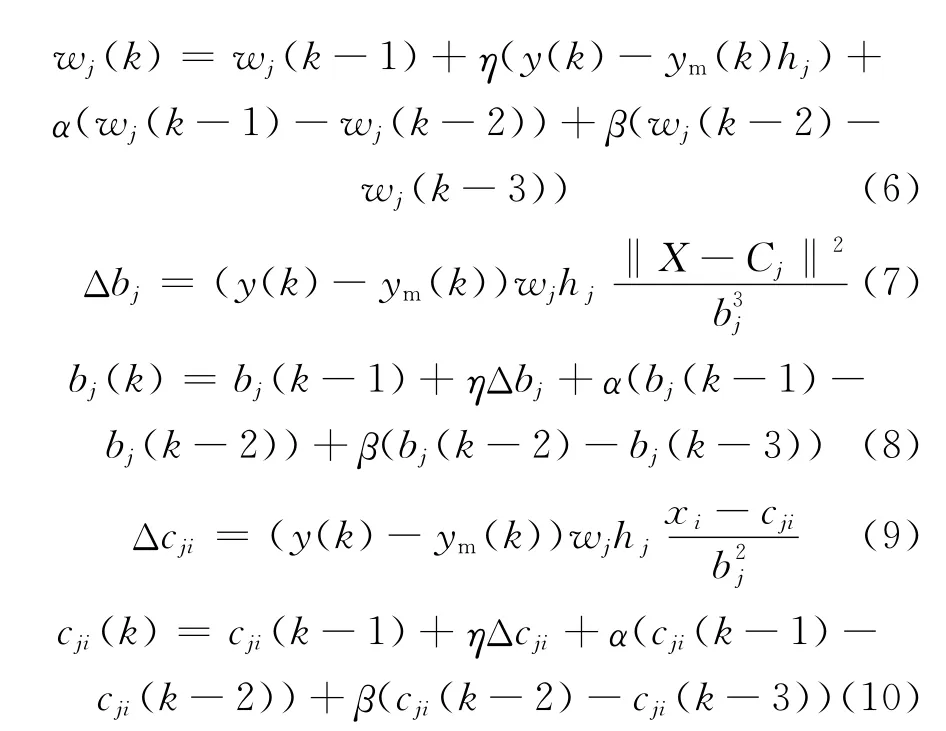
其中，i＝1，2，3；η为学习速率；α和β为惯性系数。

2.3 控制器整定原理

采用增量式PID控制器，控制误差为：

其中，r（k）和y（k）分别为系统的输入和输出。

整定指标为：

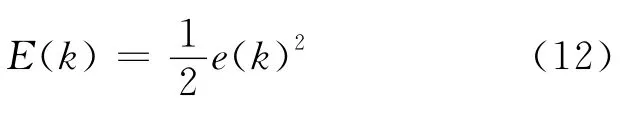
PID 3项的输入为：

其中，xc（1）、xc（2）、xc（3）分别为比例项、积分项、微分项。

PID控制器输出为：

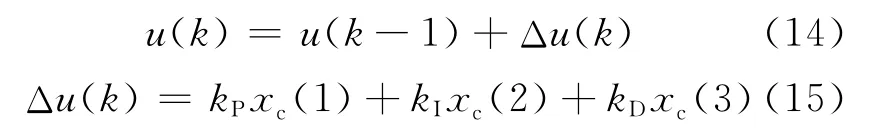
由梯度下降法得到kP、kI、kD3个参数的调整量为：

其中，∂y／∂Δu为被控对象的Jacobian信息，即对象的输出对输入的敏感度，其值可通过RBF神经网络辨识而得。

3 仿 真

为了验证RBF神经网络自整定PID控制在网络化控制系统中的有效性，利用Matlab软件中的Simulink和TrueTime仿真工具箱搭建了基于载波监听多路访问／冲突检测（Carrier Sense Multiple Access／Collision Detect，简称CSMA／CD）的介质访问控制机制的仿真平台，如图4所示。

图4 NCS仿真平台

该模型由4个TrueTime Kernel模块和1个TrueTime Network模块构成。4个内核模块分别代表传感器节点、干扰节点、控制器节点和执行器节点。其中，传感器节点设置为时间驱动型，控制节点和传感器节点设置为事件驱动类型，被控对象的传递函数为G（s）＝400／（s2＋50s）。在基于图4所示仿真平台上，分别采用常规PID控制和RBF神经网络自整定PID控制，在无时延和短随机时延 （τk∈ （0s，0.01s））情况下进行了仿真，仿真结果如图5、图6所示。

从图5、图6可以看出，在一个稳定运行的NCS中，当存在网络时延时，系统的性能恶化，超调变大，响应时间变慢。比较图5、图6发现，RBF神经网络自整定PID控制器控制下的NCS系统的性能优于传统PID控制下的性能。与常规PID控制器相比，RBF神经网络自整定PID控制器具有自适应能力强、控制精度高、鲁棒性好等优点，能有效地满足网络化控制系统的要求。

图5 无时延情况下仿真图形

图6 短随机时延情况下仿真图形

4 结束语

本文利用TrueTime工具箱建立了网络化控制系统的仿真模型，并对RBF神经网络自整定PID控制算法在网络控制系统中的应用进行了仿真研究。仿真结果表明：该控制器具有响应速度快、控制输出稳定、抗干扰能力强以及鲁棒性好等特点，能有效满足网络控制系统的要求，在解决时延对网络控制系统控制性能的影响方面有一定的实用价值。

［1］Seiler P，Sengupta R.Analysis of communication losses in

vehicle control problems［C］／／Proceedings of the American Control Conference，Vol 2.Arlington，USA：IEEE，2001：1491－1496.

［2］宋 颂，韩 东，马学森，等.基于无线传感器网络的智能公交系统［J］.合肥工业大学学报：自然科学版，2008，31（1）：21－24.

［3］Overstreet J W，Tzes A.An Internet－based real－time control engineering laboratory［J］.IEEE Control Systems Magazine，1999，19（5）：19－34.

［4］王平福，邱占芝，戴恒山.七种因素对NCS性能的影响［J］.大连交通大学学报，2009，30（3）：91－95.

［5］陈 瑞，周 征.在线自校正模糊PID控制器的研究［J］.自动化技术与应用，2008，27（12）：49－52.

［6］朱其新，胡寿松.网络控制系统的分析与建模［J］.信息与控制，2003，32（1）：5－8.

［7］赵 季，吴怀宁，吴小平.基于GPC算法的网络控制系统研究［J］.工矿自动化，2008（4）：40－43.

［8］吴洪岩，刘淑华，张 嵛.基于RBFNN的强化学习在机器人导航中的应用［J］.吉林大学学报：信息科学版，2009，27（2）：185－190.

［9］董伟杰，刘长华，宋 华.RBF和PIDNN在伺服电机模型中的应用比较［J］.控制工程，2008（Z1）：113－118.

［10］王上飞，汤汇道.自适应径向基函数神经网络［J］.合肥工业大学学报：自然科学版，2001，24（2）：244－247.

［11］李杨帆，蒋品群，罗晓曙，等.RBF神经网络在薄膜厚度控制系统中的应用［J］.现代电子技术，2010（5）：147－150.

［12］赵江东，李 娟，马小陆.基于RBF神经网络动态辨识的自整定PID控制策略［J］.工业仪表与自动化装置，2009（6）：12－15.