事件驱动的动态武器目标分配研究

梁少帅，邱涤珊，杨晓凌

（国防科学技术大学 信息系统工程重点实验室，湖南 长沙 410073）

武器目标分配（Weapon Target Allocation，WTA）问题是军事运筹学研究的重要理论问题，也是防空作战指挥决策中迫切需要解决的现实问题。当前，对静态WTA问题的研究比较深入，而动态WTA问题，由于需要考虑时间、事件等因素，相对较为复杂，目前仍无非常有效地解决方法，因而成为当前研究的一个热点。

动态WTA问题是一个NP-complete问题[1]，并具有离散性、动态性、非线性、随机性、大规模性等特点，不存在非常有效的优化算法。动态WTA主要分为武器目标分配方案和射击时机确定两个方面。目前对于动态WTA问题的研究主要集中在分配方案的求解方法上[2]，主要有分阶段求解方法[3-4]、马尔可夫过程分析方法[5-6]、anytime算法[7-8]。

从现在已公开发表的文献来看，现有的研究方法很少考虑随机出现的新目标对当前正在优化中的分配决策的影响，对于事件的处理不够灵活。新出现的目标不能在算法没有停止的时候动态地加入当前处理过程，算法总是结束对一批目标的分配后再进行对后续目标的分配。在射击时机确定问题上，有些文献[9]并没有考虑动态WTA的射击时机问题，而有些文献[8]只是简单考虑武器目标分配的截止期，并不能很好反映真实的防空作战需求。

针对上述文献的不足，根据防空作战中事件对动态WTA问题的影响，笔者提出了基于事件驱动的动态WTA改进蚁群算法，通过对事件的处理，动态地进行武器目标分配，并在满足时空约束的前提下，根据当前最优解确定目标的射击时机，在射击时机成熟时输出对目标的武器分配方案。

1 动态WTA问题描述

动态WTA主要考虑时间因素对WTA的影响，实际上是由一系列的静态WTA构成。在考虑时空约束的情况下，在一次分配方案中采用静态WTA方法，通过对到达事件的处理，动态地改变WTA问题的参数，并根据当前最优解判断是否需要对某一目标发射防空导弹。如果不需要发射防空导弹，则继续优化，否则输出对该目标的分配方案，其他目标的分配方案继续优化。

1.1WTA问题描述

WTA问题可以简单描述为M个防空单元对抗N个空中目标。典型WTA问题模型可描述如下：

其中νi为目标的威胁度，Pij为防空单元j对目标i成功拦截概率。

假定一个防空单元只能同时拦截一个目标，一个目标只可以同时被一个防空单元拦截，各个防空单元对目标的拦截概率都是独立的。目标函数的约束条件为：

为简化模型，需要将防空单元和空中目标的数量调整到同样大小。当防空单元的个数小于空中目标时，则设置相应数量的虚防空单元，虚防空单元对各目标的拦截概率为0；当目标数量小于防空单元时，则设置相应数量的虚目标，虚目标的威胁度为0。

另外，当防空单元向目标发射导弹后，该目标和所分配的防空单元处于分配冻结状态，所分配的防空单元在防空导弹与目标遭遇前不再分配给其他目标，其他导弹也不会分配给该目标。当防空单元向目标发射防空导弹后一定时间，如果评估或观测结果认为该目标未被摧毁，则目标和所分配的导弹不再处于冻结状态，重新参与武器目标分配过程。

1.2 动态武器目标分配流程

动态WTA由一系列静态WTA构成，每一次的武器分配方案由静态WTA完成，并通过对事件的处理，动态地调整静态WTA的参数，从而达到动态处理WTA问题的方法。其具体步骤如图1所示。

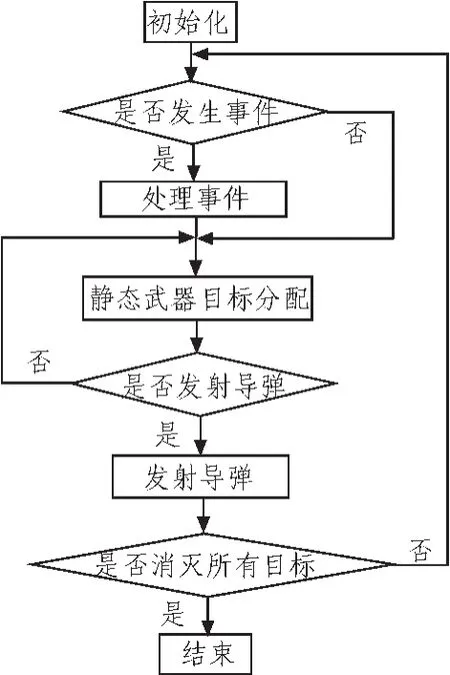
图1 动态WTA流程Fig.1 Flow chart of dynamic WTA

1.3 防空作战事件对动态WTA问题的影响

防空作战中，不同种类的事件将对武器目标分配产生不同影响。对防空作战过程产生影响的事件主要有：

1）目标信息更新 目标信息更新使得目标的威胁度和防空单元对目标的毁伤概率发生变化，从而改变武器目标分配方案。根据新的目标信息，重新计算目标的威胁度和各个防空单元对目标的拦截概率，使得分配方案体现目标信息更新的影响。

2）目标消失 当某一目标消失时，可以将该目标设置为虚目标。

3）出现新目标 出现新目标时，需要增加相应数量的虚防空单元。

4）防空单元的损毁（包括弹药耗尽）防空单元损毁或者弹药耗尽，可以将该防空单元设置为虚防空单元。

处理上述事件并不需要中断算法重新计算，原有的较优方案会对事件处理后的方案产生重要影响。当一次迭代后，可以消去相同数目的虚目标和虚防空单元，以降低计算规模。

2 动态WTA问题的改进蚁群算法求解

动态WTA问题是一个NP-complete问题，只有通过穷举方法才能得到最优解。但防空作战行动需要实时提供武器目标分配方案，这就需要分配方法能够实时输出较优的分配方案。另外，动态WTA问题需要考虑防空作战中目标信息更新、目标消失与出现、防空单元损毁等问题，需要在不中断算法执行的前提下动态更新算法参数。而蚁群算法能够很好的满足以上两个要求。

2.1 求解武器目标分配的改进蚁群算法

防空单元和目标均作为蚁群算法中的节点。蚂蚁依据目标威胁度的大小，运用轮盘赌的方法随机选择初始目标节点，并从初始目标节点按照信息素大小随机移动到未分配目标的防空单元节点上。然后依据目标威胁度的大小，运用轮盘赌的方法随机选择一个未分配防空单元节点的目标节点，并从该目标节点随机移动到未分配目标节点的防空单元节点上，直到所有目标节点都分配防空单元节点。蚂蚁只能从防空单元节点移动到目标节点，或者从目标节点移动到防空单元节点，不能在相同类型的节点间移动。

根据以上特点，可以设计改进蚁群算法的节点间信息素因子 τij和启发式因子 ηij。 当 i为目标节点，j为防空单元节点，τij为可调的信息素因子，而ηij为防空节点对目标节点拦截失败的概率 1-Pij；其他的情况下，τij和 ηij固定为0，并不参与计算。

改进蚁群算法的主要步骤是：

1）初始化操作 节点间的信息素浓度设为最小值。为提高算法的初始性能，先根据贪婪算法得到一个局部最优解，并更新信息素浓度，使得算法初期就有较优的方案。

2）节点选择 在时刻，蚂蚁从目标节点转移到防空单元节点的概率为：

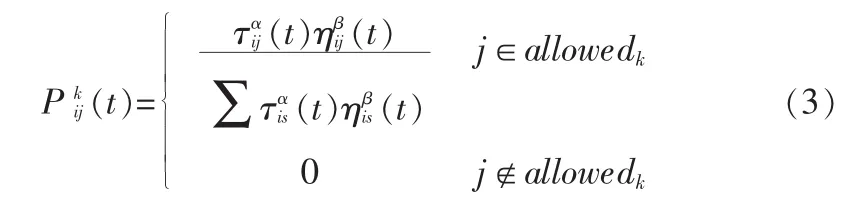
其中allowedk为当前未分配目标的防空单元节点，α、β分别为信息素因子和启发式因子的重要程度。蚂蚁从目标节点移动到防空单元节点的转移概率由信息素浓度和相应的拦截概率共同确定。为降低计算规模，可以优先在对目标节点i毁伤概率最大的K个防空单元节点中分配武器；若K个防空单元都已经分配，则从全局未分配目标的防空单元节点中分配武器。

在t时刻，蚂蚁k从防空单元节点m转移到目标节点n的概率为（t）：

（3）信息素更新

只有本次迭代最优解的蚂蚁更新局部信息素，加强正反馈的效果。根据本次迭代最优解，目标节点i和防空单元节点j间的局部信息素浓度更新为：

其中Δτ为和本次迭代最优解的目标函数值相的信息素增量。

最后，更新全局信息素浓度。目标节点和防空单元节点间的全局信息素浓度更新为：

其中ρ为信息素挥发因子。

2.2 改进蚁群算法中的事件处理

当目标信息更新时，目标的威胁度和防空单元对目标的毁伤概率发生变化，从目标节点转移到防空单元节点的概率随着毁伤概率的改变而改变，从防空单元节点转移到目标节点的概率随着目标的威胁度改变而改变。

当目标消失时，该目标设置为虚目标，其威胁度为0，从而改变防空单元转节点移到该目标节点的概率（t）；当新目标出现，则增加相应数量的虚防空单元。

当防空单元损毁或者弹药耗尽，可以将该防空单元设置为虚防空单元，其对所有目标的拦截概率0，从而改变目标节点转移到该防空单元节点的概率

2.3 动态WTA问题的射击时机确定

当空中目标一旦进入防空单元的发射区时，理论上可以尽早发射防空导弹进行拦截。但此时防空单元距离目标较远，对目标的毁伤概率较小，并不能发挥防空单元的最大作战效益。随着目标的持续临近，防空单元对该目标的毁伤概率增大，此时发射防空导弹，虽然毁伤概率增大，但降低了再次拦截的机会，一旦拦截失败，可能没有机会再次拦截。另外，如果目标是携带对地攻击导弹的飞机，在持续临近中有可能构成发射对地攻击导弹的条件，此时，不但需要拦截飞机，还需要拦截对地攻击导弹，直接影响作战效益。

文中将空中目标分为飞机和对地攻击导弹两种类型，并假定防空导弹的射程大于对地攻击导弹的射程。因为需要考虑飞机所携带的对地攻击导弹，本文定义威胁跃升点这一概念，如果防空单元在飞机处于该点时发射防空导弹，则可以在飞机所携带的对地攻击导弹的最大发射距离上遭遇飞机，如果拦截成功，飞机无法发射对地攻击导弹。

当飞机位于威胁跃升点之外时，如果飞机i的威胁度和防空单元j对其的毁伤概率的乘积大于一个阈值δ，即νiPij＞δ，则对该目标发射防空导弹。当飞机位于威胁跃升点以内时，则尽早发射防空导弹，以减少飞机发射对地攻击导弹的机会，减少需要拦截目标的数量，并增加拦截失败后再次拦截的机会。

对于对地攻击导弹，则尽早发射防空导弹，增加拦截失败后再次拦截的机会。

在动态WTA的改进蚁群算法中，如果根据当前最优解或者本次迭代最优解得到目标满足发射防空导弹的条件，则分配对应的防空单元拦截该目标，其他目标继续持续优化。当某一目标的射击条件满足时，只需要输出该目标的武器分配决策，其他目标可能还有充分的优化时间，也就是说算法以“一个目标接一个目标”的方式进行武器分配。如果匆匆输出所有目标的分配决策，可能使拦截效果大大下降。

3 仿真结果

在仿真实验中，假设初始时防空单元和空中目标的数量分别为100，目标的威胁度在0.0～1.0之间随机生成，防空单元对各个目标的毁伤概率在0.2～0.9之间随机产生。蚁群算法中，信息素因子α、启发式因子β、信息素挥发因子ρ分别为和 1.0、1.0、0.3。 在蚁群算法的 100 次迭代中，在 21、41、61、81次迭代时分别出现目标状态更新、目标消失、新目标出现、防空单元损毁等事件。基于事件驱动的动态WTA蚁群算法可以平滑地处理事件，算法的目标函数值没有较大波动；而多阶段的动态WTA蚁群算法在事件发生时，只是简单的中断算法并按照新的数据重新进行计算，目标函数值会出现较大波动，其整体优化性能低于基于事件驱动的动态WTA蚁群算法，如图2所示。另外，当迭代次数增加时，改进蚁群算法的性能优于贪婪算法。为降低计算规模，可以优先在对目标节点毁伤概率最大的K个防空单元节点中分配武器。若K个防空单元都已分配目标，则从全局未分配目标的防空单元节点中分配武器。

仿真实验考查了防空单元和空中目标的数量分别为100的规模下，蚁群算法迭代200次，K取值对当前最优解的目标函数值、运行时间以及两者乘积的影响，如图3、图4、图5所示。通过分析可得，当K较大时，算法中可优先选择的防空单元节点较多，收敛较慢，运行时间长；当较小时，目标节点可以优先选择的防空单元节点可能已经分配目标，只能从全局去寻找最优解，收敛较慢，运行时间长；当K取3～7时，目标函数值与运行时间都较小，算法能够得到满意的性能。

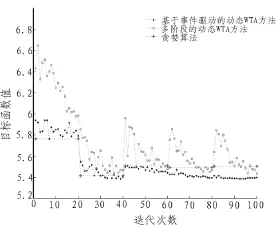
图2 目标函数值比较Fig.2 Comparing the objective function value

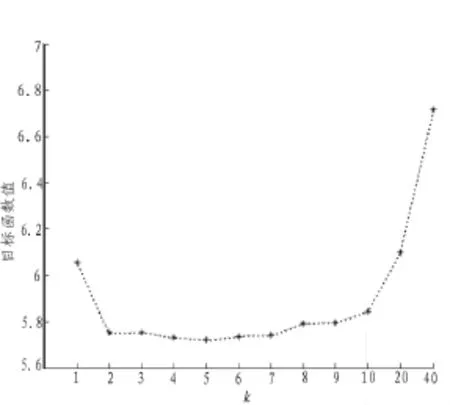
图3 K对目标函数值的影响Fig.3 The impact of K on the objective function value

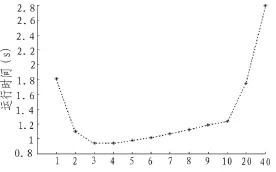
图4 K对运行时间的影响Fig.4 The impact of K on the running time

4 结束语

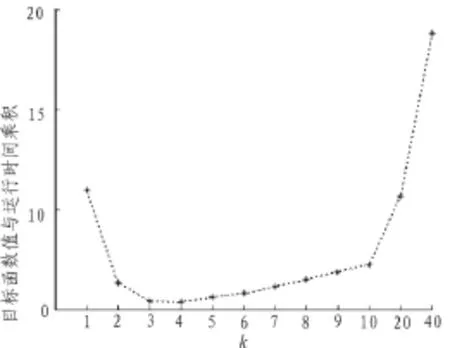
图5 K对目标函数值和运行时间乘积的影响Fig.5 The impact of K on the product

动态WTA问题，由于考虑时间等因素，相对复杂，目前仍无非常有效的解决方法，因而成为当前研究的一个热点。本文针对当前动态WTA问题研究中的不足，提出了基于事件驱动的动态武器目标分配的改进蚁群算法。通过处理事件，动态地改变蚁群算法的参数，使算法的优化体现动态特性，并且原有的优化方案对事件处理后的方案产生影响。改进蚁群算法运算速度快，解的质量基本令人满意，可用于解决较大规模的动态WTA问题。仿真实验表明了算法的有效性。

[1]Lloyd S P， Witsenhausen H S.Weapons allocation is NP－complete[C]//Proceedings of the IEEE Summer Simulation Conference， 1986：1054－1058.

[2]刘传波，邱志明，吴玲，等.动态武器目标分配问题的研究现状与展望[J].电光与控制， 2010， 17（11）:43－47.LIU Chuan-bo， QIU Zhi-ming， WU Ling， et al.Review on current status and prospect of researches on dynamic weapon target assignment.Electronics optics&control， 2010， 17（11）:43－47.

[3]Hosein P， Walton J， Athans M.Dynamic weapon－target assignment problems with vulnerable C2 nodes[R].LIDS_P_1786，MIT，1988.

[4]Hosein P， Athans M.An asymptotic result for the multistage weapon target allocation problem [R].LIDS－P－945，MIT，1990.

[5]杨祖快，刘鼎臣.基于马尔可夫决策过程动态WTA最优化模型分析[J].火力与指挥控制， 2003， 28（5）:25－27.YANG Zu-kuai， LIU Ding-chen.Optimization model analysis of dynamic WTA based on Markov Decision-making[J].Fire Control&Command Control， 2003， 28（5）:25－27.

[6]蔡怀平，刘景旭，陈英武.动态武器目标分配问题的马尔可夫性[J].国防科技大学学报， 2006， 28（3）:124－127.CAI Huai-ping， LIU Jing-xu， CHEN Ying-wu.On the markov characteristic of dynamic weapon target assignment problem[J].JournalofNation University ofDefense Technology， 2006， 28（3）:124－127.

[7]Khosla D.Hybrid genetic approach for the dynamic weapontarget allocation problem[C]//Proceeding of SPIE， 2001，4396:248-263.

[8]WU Ling， WANG Hang-yu， LU Fa-xing.An anytime algorithm based on modified GA for dynamic weapontarget allocation problem[C]//WCCI， Hong Kong， China，2008:234-238.

[9]蔡怀平，陈英武，邢立宁.SVNTS算法的动态武器目标分配问题研究[J].计算机工程与应用，2006，42（31）:7-10 CAI Huai-ping， CHEN Ying-wu， XING Li-ning.Research on dynamic weapon target assignment problem based on SVNTS algorithm[J].Computer engineering and applications， 2006，42（31）:7-10.