一种基于精简粒子群优化的霍夫变换算法

张英涛，黄剑华，唐降龙，刘家锋

(哈尔滨工业大学计算机科学与技术学院，哈尔滨 150001)

一种基于精简粒子群优化的霍夫变换算法

张英涛，黄剑华，唐降龙，刘家锋

(哈尔滨工业大学计算机科学与技术学院，哈尔滨 150001)

为了提高现有霍夫变换算法的准确率及计算效率，提出了一种基于精简粒子群优化的霍夫变换算法．该方法将霍夫变换后解的参数作为粒子位置，将霍夫变换的累加数组值作为粒子的适应度值，每一次迭代更新粒子的位置和速度，并将所得粒子群的适应度值按降序排列，保留“强壮”粒子，组成精简粒子群．实验结果表明，基于精简粒子群优化的霍夫变换算法不仅可以提高霍夫变换的计算速度，而且可以获得较高的计算准确率，特别是对于复杂背景图像和高噪声图像也同样适用．

霍夫变换；精简粒子群优化；图像处理；曲线检测

霍夫变换算法是检测图像中特定形状的基本方法[1-2]，由于其对随机噪声不敏感，对不完整边缘具有鲁棒性，而且适用于并行处理，因此被广泛应用于计算机视觉和模式识别等领域[3-4]．标准霍夫变换(standard Hough transform，SHT)可用于直线、圆以及椭圆检测；广义霍夫变换(generalized Hough transform，GHT)可用于检测任意形状．从1962年霍夫变换方法首次被提出至今，该方法经历了不断的改进和发展，如分层霍夫变换(Hierarehieal HT，HHT)[5]、概率霍夫变换(probabilistic HT，PHT)[6]、自适应霍夫变换(adaptive HT，AHT)[7]、模糊霍夫变换(fuzzy HT，FHT)[8]和扩展霍夫变换(extended HT，EHT)[9]．

然而霍夫变换计算量大、耗时，很难达到实时处理要求[10]，因此许多学者致力于研究检测准确率高且快速的霍夫变换方法．Galambos等[11]使用梯度信息减小计算量，以加速算法．Matas等[12]提出一种改进的概率霍夫变换，采用随机取点映射、映射和直线检测交替进行，运算过程可在所有待处理点完成向参数空间的映射或被归类到某一直线上后停止．这时，只有小部分待处理点完成映射，其余点即作为被检测到的直线上的点，从待处理点集中去除，而不必进行向参数空间的映射，减少了运算开销．Duquenoy等[13]提出一种伪线性方法，应用欠采样技术及预先最大检测技术来加速计算．文献[14]提出一种严格的随机霍夫变换方法，用小的随机样本集取代全部样本集进行预处理，减少错误选择点．

笔者提出一种精简粒子群优化(reduced particle swarm optimization，RPSO)算法，并与霍夫变换相结合，将霍夫变换后解的参数作为粒子位置，用霍夫变换的累加数组值作为粒子的适应度值，迭代更新粒子的位置和速度，把所得粒子群的适应度值按降序排列，保留“强壮”粒子，组成精简粒子群．在实验部分分别给出了基于精简粒子群优化的霍夫变换算法对各种不同类型噪声的模拟图像及实际图像检测直线、圆及椭圆的结果．实验结果表明，所提算法不仅可提高霍夫变换的计算速度，而且可以获得较高的计算准确率，特别是对于复杂背景图像和高噪声图像，可以获得较好的性能．

1 精简粒子群优化算法

1.1 粒子群优化算法

粒子群优化算法(particle swarm optimization，PSO)是一种基于群体的演化算法，它利用自然选择和遗传学的思想，通过模拟生物群落系统的进化机制来完成加速和改善随机搜索的算法．最早的PSO算法模拟一些简单的社会群落生物，如鸟群、鱼群等模型，由Kennedy等[15]于1995年提出．

PSO算法可描述如下：

在n维解空间，粒子可表示为xi＝(xi1，xi2，…，xin)，即粒子在搜寻空间中的位置，是问题的一个解，粒子速度可表示为vi＝(vi1，vi2，…，vin)，则粒子寻优公式可表示为

式中：Pinbest、Pngbest分别为粒子群的个体最优位置和群体最优位置的n维向量；rand1、rand2是两个0～1间的随机数；c1、c2为加速度系数；w为惯性因子；k为优化迭代次数．

1.2 精简粒子群优化算法

精简粒子群优化(RPSO)算法是一种改进型的粒子群优化(PSO)算法．其基本思想是：在PSO算法中，M个粒子被初始化．在每次迭代中，粒子的速度和位置都相应更新，计算该位置的适应度，并根据适应度把群中粒子按降序排列，每次选择排在前面的粒子(精简比例为r)作为精简粒子群，其余粒子被淘汰．该过程进行迭代，直到达到最大迭代次数或者错误率小于预先设定的最小阈值．这种改进能够有效降低传统PSO算法的计算时间，且提高解的精度．

精简粒子群优化的具体过程描述如下：

(1) 选择1个具有M个粒子的种群，命名为初始种群S(1)＝{P1，P2，…，PM}，初始化每个粒子的位置xin；

(2) 随机初始化每个粒子的飞行速度vin；

(3) 计算每个粒子的适应度f(xin(k))；

(4) 在1k+次迭代中，比较每一个粒子的最佳位置适应度和当前位置适应度，根据适应度更新每个粒子的位置Pin(k+1)，即

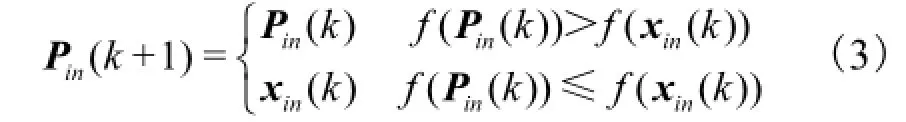
(5) 选择当前全局最佳适应度的位置为k+1次全局最佳位置Pngbest(k+1)；

(6) 根据适应度对群中粒子降序排序，选择排在前面的粒子(精简比例为r)来形成精简的下一代粒子群S(k+1)；

(7) 更新k+1代中每个粒子的速度vin(k+1)；

(8) 更新k+1代种群S(k+1)中每个粒子的位置；

返回第(3)步，重复以上过程直到迭代结束．

惯性因子w用于调整算法全局和局部搜索能力的平衡．w值较大，有利于跳出局部极小点，从而找到全局最优解；w值较小，则有利于算法收敛．因此，为进一步优化算法，采用一种自适应调整w值的策略．令w=1.5Mk/kM,其中Mk为第k次迭代时粒子群的数量．这使得算法在前期有较高的探索能力，而在后期有较高的开发能力以加快收敛速度．加速度系数c1、c2设为常数2．

2 基于精简粒子群优化的霍夫变换算法

将RPSO算法与霍夫变换相结合，提出了基于精简粒子群优化的霍夫变换算法．把霍夫变换后的解参数当作粒子的位置，使用RPSO算法寻找最优解，将霍夫变换的累加数组值作为适应度值．“精简粒子群”的选择有助于提高运算速度，找到精确的最优解．

式(4)为极坐标中表示一条直线的参数方程．

图像空间中的点(,)x y经霍夫变换映射到参数空间中的一条正弦曲线，图像空间中共直线的点映射到参数空间中的正弦曲线的交点就对应原直线的2个参数ρ和θ．下面以采用极坐标的直线检测为例，说明基于精简粒子群优化的霍夫变换算法的具体过程．

(1) 选择一个具有M个粒子的种群，命名为初始种群S(1)＝{P1，P2，…，PM}，为霍夫变换参数ρ和θ赋初值0ρ、0θ，并将2 维累加数组A初始化为零；

(2) 对一原始图像I进行边缘提取，求得边缘点集E；

(3) 在边缘点集E中随机选取两个点1pt、2pt，使用这两个点计算直线的参数，并使用所得参数值初始化该粒子在粒子群中的位置xin；

(4) 重复步骤(3)直至粒子群中所有粒子值初始化完毕；

(5) 随机初始化每个粒子在粒子群中的速度vin；

(6) 计算每个粒子的适应度值f(xin(k,ρk,θk))，即

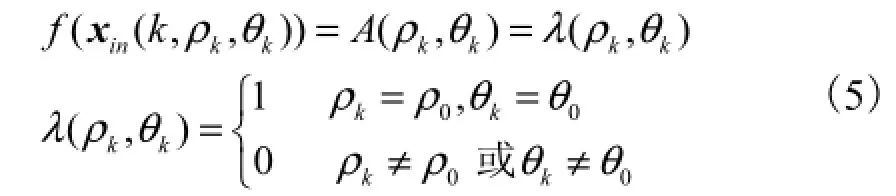
(7) 在k+1次迭代中，使用式(3)比较每一个粒子的最佳位置适应度和当前位置适应度，根据适应度更新每个粒子的位置Pin(k+1)；

(8) 选择当前全局最佳适应度的位置为k+1次全局最佳位置Pngbest(k+1)；

(9) 根据适应度对群中粒子降序排序．选择排在前面的粒子(精简比例为r)来形成精简的下一代粒子群S(k+1)；

(10) 根据式(4)更新k+1代中每个粒子的速度vin(k+1)；

(11) 更新k+1代种群S(k+1)中每个粒子的位置；

(12) 返回第(6)步，重复以上过程直到迭代结束．

3 实验结果

实验采用Matlab7.1，在一台3.2,GHz、2,G内存的Pentium 4 PC机上运行．初始化粒子数M为100，精简比例r为90%．

为验证所提出算法的有效性，本节给出了模拟图像及实际图像检测的结果．图1为512 512×的模拟图像，其中包含2个直径分别为50像素、80像素的圆；1个长轴半径和短轴分别为160像素、120像素的椭圆；1个420 420×像素的正方形．图2～图4所示的3组模拟图像，分别加入不同程度的高斯白噪声、椒盐噪声及斑点噪声，用来测试本算法在各种噪声条件下的性能．图4所用的斑点噪声模型在文献[16]中有详细描述．图5为本算法对实际图像的检测结果．

图1 模拟图像Fig.1 Synthetic image

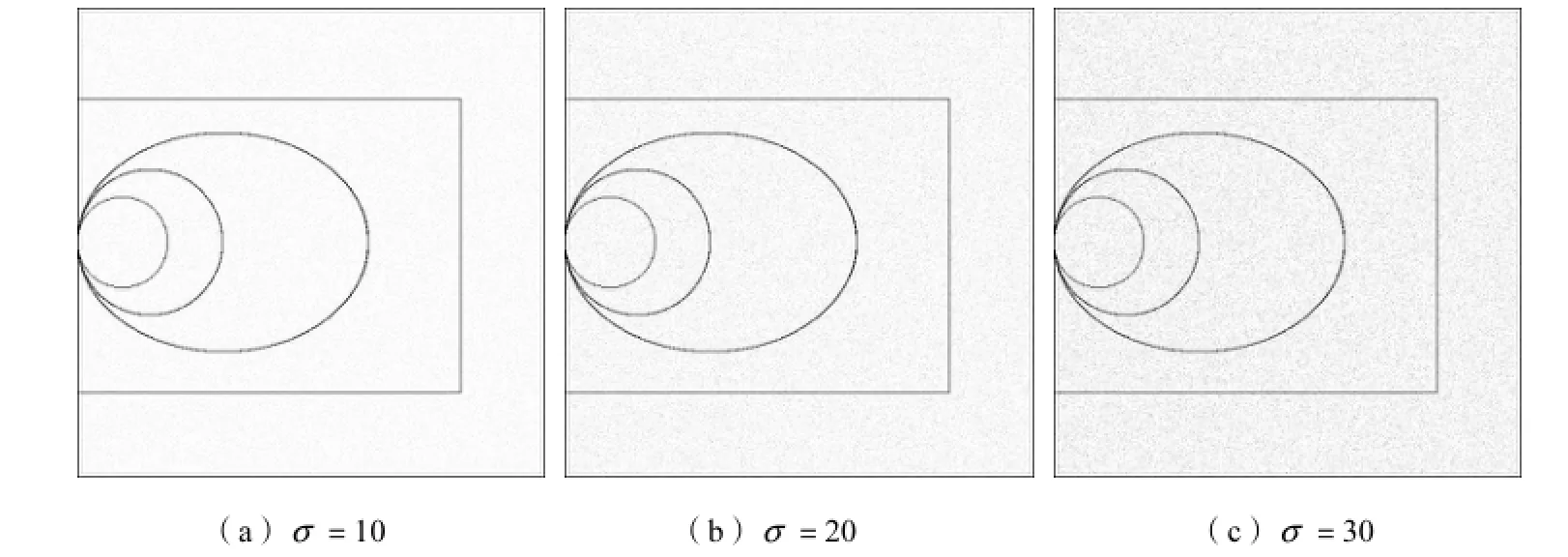
图2 含有不同等级高斯噪声的检测图像(噪声均值为0)Fig.2 Images for line detection with Gaussian noise，whose mean m＝0 and standard deviations σ having different values

图3 含有不同等级椒盐噪声的检测图像Fig.3 Images for circle detection having salt and pepper noise with different level values

图4 具有不同等级斑点噪声检测图像Fig.4 Images for ellipse detection having speckle noise with different level values

表1 本文所提出算法和RHT算法对图2处理结果的比较Tab.1 Comparisons of processing the images in Fig.2 between the proposed approach and RHT

表2 本文所提出算法和RHT算法对图3处理结果的比较Tab.2 Comparisons of processing the images in Fig.3 between the proposed approach and RHT

为比较算法对不同目标的检测准确率，定义检测误差为

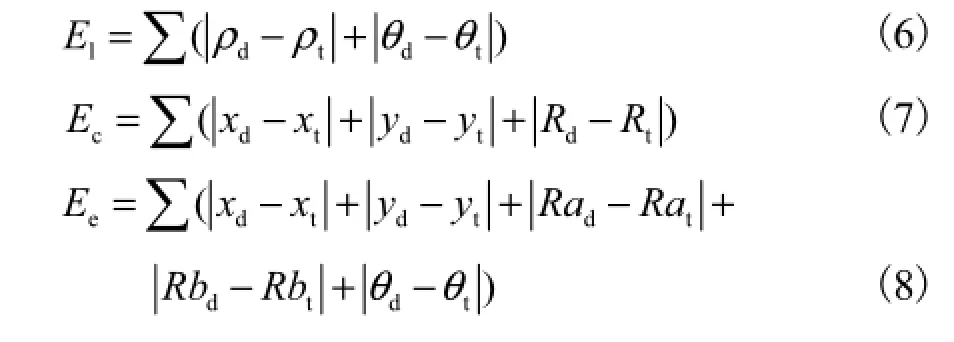
式中：lE、cE、eE分别为检测直线、圆、椭圆误差，即定义误差为所有检测参数与实际参数差的绝对值累加和；ρd、θd、xd、yd、Rd、bd为检测值；ρt、θt、xt、yt、Rt、bt为实际值．表1～表3分别为图2～图4的检测结果，用以作为本文提出算法与Regularized HT[1]及限制随机霍夫变换算法(RRHT)[14]的性能比较．由表1～表3的结果对比可知，本算法具有较高效率，比其他算法快得多(＞45%)，并且可以获得较精确的检测结果；特别是在噪声级别较高的图像中，检测准确率优于Regularized HT及RRHT算法．

图5为本算法对实际图像中直线和圆的检测结果，图5(c)中背景模糊且有多个目标重叠，本算法将其中的8个圆全部准确地检测出来．

表3 本文所提出算法和RHT算法对图4处理结果的比较Tab.3 Comparisons of processing the images in Fig.4 between the proposed approach and RHT

图5 本方法对实际图像中直线和圆的检测结果Fig.5 Results on the real images for line and circle detection

4 结 语

本文首先介绍精简粒子群优化(RPSO)算法，并将其与霍夫变换相结合，提出了基于精简粒子群优化的霍夫变换算法，最后以检测直线为例给出霍夫变换具体过程．

本方法从优化的角度对霍夫变换进行了改进，提高了霍夫变换的检测准确率，并节省了计算时间．大量实验表明，本方法在高噪声和复杂背景下均可获得较好的性能．本文的方法对于图像特定形状的目标检测具有较为广泛而重要的实用价值．

［1］ Aggarwal N，Karl W C. Line detection in images through regularized Hough transform[J]. IEEE Transactions on Image Processing，2006，15(3)：582-591.

［2］ Hahn K，Jung S，Han Y，et al. A new algorithm for ellipsedetection by curve segments[J]. Pattern Recognition Letter，2008，29(13)：1836-1841.

［3］ Bonci A，Leo T，Longhi S. A bayesian approach to the Hough transform for line detection[J]. IEEE Transactions on Systems，Man，and Cybernetics，2005，35(6)：945-955.

［4］ Leemans V，Destain M F. Application of the Hough transform for seed row localisation using machine vision[J]. Biosystems Engineering，2006，94(3)：325-336.

［5］ Guerra C，Hambrush S. Parallel algorithm for line detection on a mesh[J]. J Parallel Distributed Computing，1989，6：l-19.

［6］ Kiryati N，Eldar Y，Bruckstein A M. A probabilistic Hough transform[J]. Pattern Recognition，1991，24(4)：303-316.

［7］ Atiquzzaman M. Multiresolution Hough transform：An efficient method of detecting patterns in images[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence，1992，14(11)：1090-1095.

［8］ Han J H，Koczy L T，Poston T. Fuzzy Hough transform [J]. Pattern Recognition Letters，1994，15(7)：649-658.

［9］ Cha J，Cofer R H，Kozaitis S P. Extended Hough transform for linear feature detection[J]. Pattern Recognition，2006，39(6)：1034-1043.

［10］ Xu L. A unified perspective and new results on RHT computing，mixture based learning，and multi-learner based problem solving[J]. Pattern Recognition，2007，40 (8)：2129-2153.

［11］ Galambos C，Kittler J，Matas J. Using gradient information to enhance the progressive probabilistic Hough transform[C]// Proceedings of the International Conference on Pattern Recognition. Barcelona，Spain，2000：560-563.

［12］ Matas J，Galambos C，Kittler J. Progressive probabilistic Hough transform[C]// Proceedings of British Machine Vision Conference. Southampton，UK，1998：256-265.

［13］ Duquenoy E，Taleb-Ahmed A. Applying the Hough transform pseudo-linearity property to improve computing speed[J]. Pattern Recognition Letters，2006，27(16)：1893-1904.

［14］ Cheng Z，Liu Y. Efficient technique for ellipse detection using restricted randomized Hough transform[C]// Proceedings of International Conference on Information Technology. Las Vegas，USA，2004：714-718.

［15］ Kennedy J，Eberhart R C. Particle swarm optimization [C]// Proceedings of IEEE International Conference on Neural Networks. Perth，Australia，1995：1942-1948.

［16］ Yue Y，Croitoru M M，Bidani A，et al. Nonlinear multiscale wavelet diffusion for speckle suppression and edge enhancement in ultrasound images[J]. IEEE Transactions on Medical Imagings，2006，25(3)：297-311.

A Hough Transform Algorithm Based on Reduced Particle Swarm Optimization

ZHANG Ying-tao，HUANG Jian-hua，TANG Xiang-long，LIU Jia-feng
(School of Computer Science and Technology，Harbin Institute of Technology，Harbin 150001，China)

To improve the accuracy and efficiency of existing Hough transform algorithms，a novel Hough transformation algorithm based on reduced particle swarm optimization(RPSO) is presented. The parameters of the solution after Hough transformation are employed as particle positions，and an accumulation array in Hough transformation is utilized as a fitness function of RPSO algorithm. Velocities and positions are updated accordingly，and position fitness values are calculated and sorted in a list with the descending order. “Stronger” particles whose fitness values are in the higher positions of the list are selected and the reduced particle swarm is then obtained. The experimental results show that the proposed approach can detect curves more accurately with less computational time，especially for images with complex background or with high level noise.

Hough transform；reduced particle swarm optimization；image processing；curve detection

TP391.4

A

0493-2137(2011)02-0162-06

2009-09-28；

2009-12-24.

国家自然科学基金资助项目(60873142，30670546)；黑龙江省青年基金资助项目(QC08C20)；哈尔滨工业大学创新基金资助项目(HIT.NSRIF.2008.48).

张英涛（1975— ），女，博士，讲师.

张英涛，yingtao@hit.edu.cn.