均匀圆阵来波方向估计的解模糊算法

冷 文，王安国

(天津大学电子信息工程学院，天津 300072)

平面阵天线与线阵天线相比，在测向方面有许多优异之处[1]，可以同时估计来波方向(direction of arrival，DOA)的方位角和俯仰角，而且方位角估计范围相比线阵要扩大很多．均匀圆阵是一种典型的平面阵，其阵元均匀分布在一个圆周上，由于其结构特点使其在任何方向都具有近似相同的估计精度和分辨率[2]．

正如线阵天线在测向时由于阵元间距大于半波长导致测向模糊一样[3]，均匀圆阵天线也存在同样的问题．而从提高天线阵测向精度和减小阵元间互耦考虑，在天线设计时希望天线阵的孔径尽可能的大，因此通过天线阵调整解决大半径均匀圆阵天线测向模糊的研究在实际应用中具有非常重要的意义．

笔者首先从导向矢量的角度研究造成模糊现象的原因；然后从修正导向矢量入手，以四元和六元均匀圆阵为模型，通过调整阵元位置的方法修改均匀圆阵的导向矢量，打破在大半径情况下 DOA估计中由真实角度和虚假角度形成的导向矢量完全相同的平衡，利用这个结果极大地抑制了模糊现象对应的伪峰幅度，提高了来波方向估计的精确度；最后通过引入虚拟阵列变换方法解决了上述算法必须修改现有圆阵结构的缺陷．

1 大半径均匀圆阵 DOA估计中真实角度和虚假角度的关系

对于圆阵天线，设阵元数为M，各个阵元的位置可以用极坐标形式表示为(ri,θi) ，i＝1，2，…，M，其中ri为该阵元到参考原点的距离，θi为与X轴正向的夹角，因此圆阵天线的导向矢量可以写为

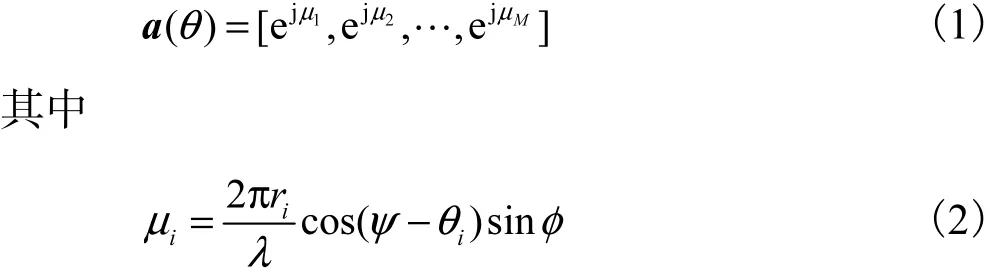
式中：λ为入射信号源波长；ψ为入射方位角；φ为入射俯仰角．

由于复指数函数 ejμ对于μ具有以2π为周期的周期性[4-5]，因此对于一个确定的a(θ)，不一定保证信号方向估计的唯一性，即存在模糊现象．而模糊的定义是除了真实的入射角度以外还存在 1个或多个虚假的入射角度，而真实角度和虚假角度形成的导向矢量相同[6]，即

式中：ψ和φ为真实的方位角和俯仰角；fψ和fφ为可能虚假的方位角和俯仰角．

导向矢量相同也就代表着该矢量的各个分量相同，即

式中：μi为真实矢量的分量；μif为可能的虚假矢量的分量；i = 1 ,2,… ,M ；Ki为整数(含负整数、零和正整数)．将式(4)按照式(2)的定义展开化简后得到真实角度和可能的虚假角度之间的关系表达式为

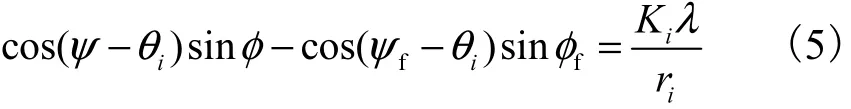
2 均匀圆阵抑制伪峰的原理介绍

根据文献[7]的分析结论，均匀圆阵在半径一定的条件下，阵元数越多出现来波估计模糊的可能性越小，并且估计模糊主要集中在四元和六元圆阵的一阶模糊，此时对于来波方向估计精度的影响最大，而其他阵元数的均匀圆阵由于主要是二阶模糊，对于来波方向估计精度影响较小，因此本文主要分析、介绍四元和六元圆阵模糊现象的抑制过程．

六元均匀圆阵见图 1(a)，半径为r，结合每个阵元的特点，式(5)可以展开得到式(6)[8-9]．

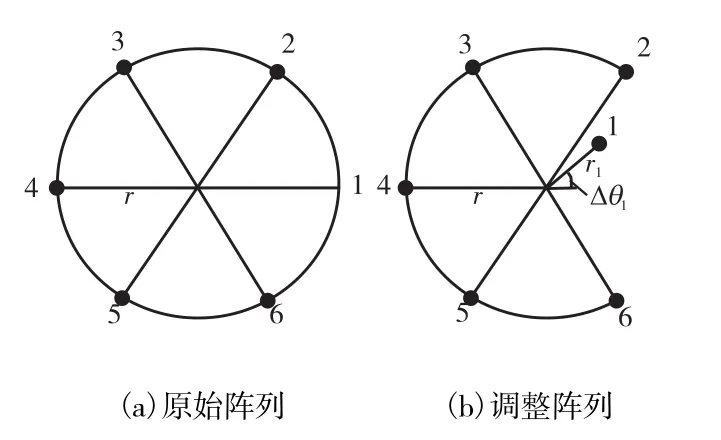
图1 两种不同的六元圆阵Fig.1 Two different six-elements circle arrays

显然，真实的方位角和俯仰角等于估计的方位角和俯仰角，没有模糊现象出现．

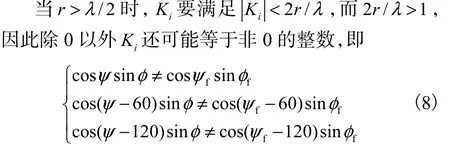
ψ和φ有可能与φf和ψf不相等，出现模糊现象．

针对这种情况，可以考虑在六元均匀圆阵中调整某个阵元，见图 1(b)中的阵元 1，该阵元半径为1r，新位置的阵元和原阵元与X轴夹角的偏差为Δθ1，式(6)改写为

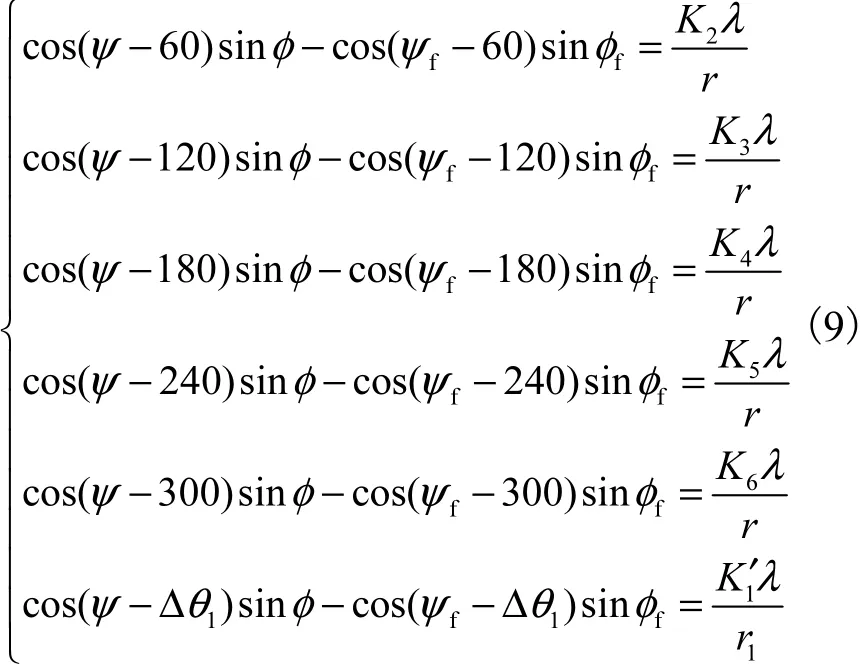
根据式(9)中 K2=-K5及K3=- K6的特点，将式(9)化简展开得到

在半径 r大于半波长情况下，K2～K6在满足|Ki|＜2r/λ条件下都有可能为非0值，如果要实现无模糊估计，而 K1′又必须为整数，就要求

在此限定Δθ1的变换范围在相邻两个阵元之间，即±60°，因此半径r1和偏角Δθ1相互配合可以保证K1′只能取值为0才可以保证式(12)的成立．如当Δθ1为0°或为 60°，即新阵元没有偏移角度或者新阵元调整到与相邻下方阵元相同方向位置的时候，可以用r1=(1/2)λ来抑制模糊；而当 Δθ1为-60°，即阵元调整到与相邻上方阵元相同方向的位置，则可以用r1= ( 1/4)λ来抑制模糊．其他角度时，则半径 r1的调整范围界于上述范围之内．

四元均匀圆阵的分析过程与六元均匀圆阵类似，在此省略，仅对以四元均匀圆阵为例的阵元调整位置的影响结果加以说明．参照式(11)～(13)的推导，可以得出在四元均匀圆阵中的对应结果为

式中：r1为调整阵元的有效半径；1θΔ为该调整阵元调整后与原阵元的角度偏移量．半径r1和偏角1θΔ相互配合可以实现在四元均匀圆阵中对模糊现象的抑制．

3 算法验证

设定四元均匀圆阵半径为 2倍波长，信噪比20,dB，入射方位角40°，俯仰角60°，真实角度估计结果为(40°，60°，65.13,dB)，而阵元调整包括调整半径和偏移角度，测试结果见表 1．从结果可以看出通过阵元调整、修改有效半径和偏移角度可以实现伪峰的大幅度消减．

表1 不同阵元调整结果比较Tab.1 Comparison of the results with the different element adjustments

针对该算法的普适性，本文进行了验证．设六元均匀圆阵半径为 2倍波长，信噪比 10,dB，调整的阵元与圆阵圆心的半径为 0.2倍波长，偏移角度 0°．为了验证上述算法，针对不同入射角度的广泛有效性，将信号源入射方位角设定为 0°～180°变化，俯仰角为 0°～90°变化，计算每个入射角度对应估计的真实角度峰值与最大伪峰峰值之差，结果显示在图 2．其中两个平面坐标是入射方位角和俯仰角，间隔为 5°，Z轴坐标是以分贝表示的估计真实角度峰值与最大伪峰峰值的差，重复计算次数为 50次．图 2显示最小的峰值差为 35 dB，因此从仿真结果上看该算法具有广泛有效性，可以极大地提高DOA估计精度．

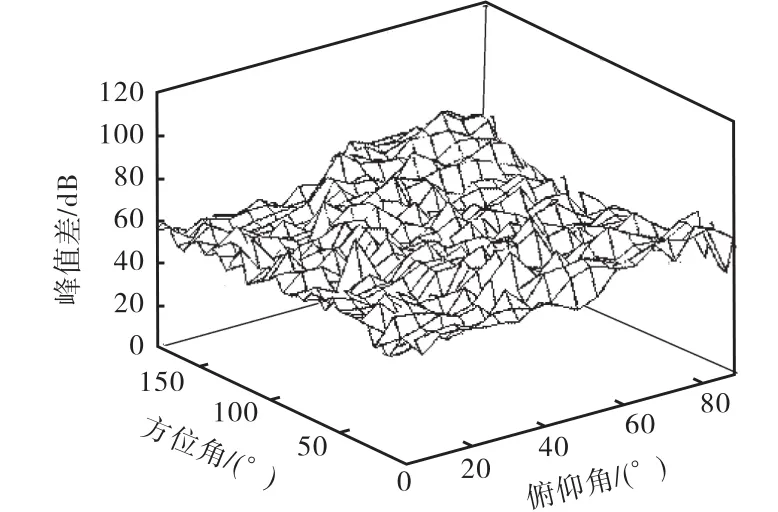
图2 阵元调整普适性分析结果Fig.2 Analysis result for universal of element adjustment

4 虚拟阵列变换方法的实现

上述算法对于均匀圆阵的设计提出了调整天线阵元的要求，在现有天线阵列结构的基础上调整天线阵元增加了设计复杂度，同时也会降低由大半径带来的提高天线有效孔径、降低天线阵元间互耦等特性．针对上述算法在设计实现方面的缺陷，本文引入虚拟阵列变换方法将真实圆阵(图 1(a))转换为对应的虚拟阵列(图1(b))．

通过虚拟阵列变换进行来波方向估计，已有许多论述[10-12]．利用这种变换方法可实现将任意阵列变换成等距均匀线阵或其他具有相同结构的阵列，然后基于变换后的阵列进行信号处理．而虚拟阵列变换最主要的性能指标是变换误差和变换区域长度[7-8]．变换误差直接影响到估计的精度和分辨率，变换误差表示为

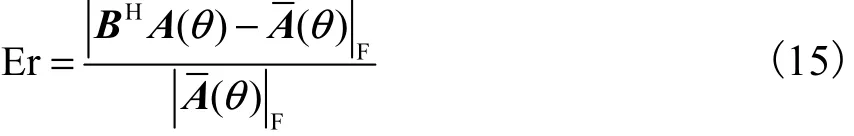
式中：B为变换矩阵；A(θ)为真实阵列的阵列流型；(θ)为虚拟阵列的阵列流型表示计算 Frobenius范数．

变换区域是指计算变换矩阵B的区域范围．变换区域的长度越小，在区域内的变换误差越小．但是由于需要在每个变换区域内进行数据协方差矩阵的特征值求解和角度扫描，因此变换区域过小会造成运算量大幅度增加，直接影响到来波方向估计的实时性能．

从式(15)可以看出，变换误差是跟真实阵列和虚拟阵列之间差异的大小有关，当两个阵列的差异非常大时，变换误差也很大，而图 1(a)所示的真实阵列与所对应的虚拟阵列图 1(b)的唯一差异就是虚拟阵列将真实阵列的一个阵元调整到接近中心的位置．图 3是图1中真实阵列和变换后的虚拟阵列的变换误差，俯仰角和方位角的变换区域均为 0°～30°．从结果可以看出由于只调整某个阵元接近中心，阵列结构变化不大，相对于文献[6]中列举案例的变换误差，该变换带来的变换误差比较小．

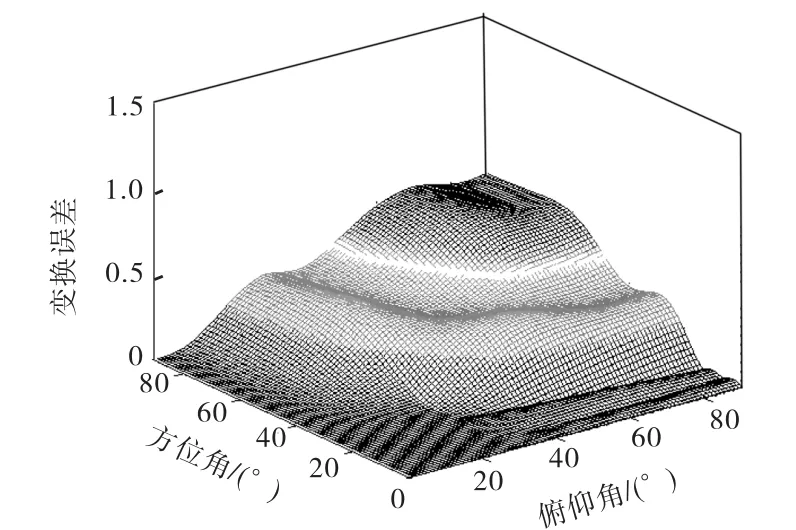
图3 图1(a)到图1(b)的变换误差Fig.3 Transformation error from Fig.1(a) to Fig.1(b)

表 2是对表 1中阵元调整结果采用虚拟阵列变换后进行估计的结果．从中可以看出由于虚拟阵列误差的引入最大的伪峰大于表1对应的最大伪峰，但考虑到表 1案例的俯仰角和方位角都属于 0°～30°变换区域以外的变换误差较大区域，而得到的最大伪峰与真实角度估计结果的峰值差依然高于 20,dB，因此采用虚拟阵列变换的辅助方法是可行的．

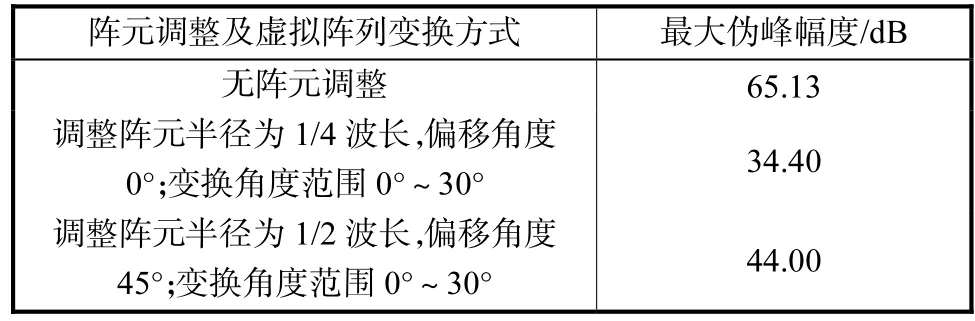
表2 不同阵元调整后采用虚拟阵列变换后的结果比较Tab.2 Comparison of the results by the virtual array transformation after the different element adjustments

5 结 语

本文分析了均匀圆阵DOA估计出现模糊现象的原因，在此基础上提出了通过对四元和六元均匀圆阵的简单调整来修正导向矢量的方法改善模糊现象、抑制伪峰的算法．而调整阵元的天线设计要求还可以通过虚拟阵列变换的辅助方法来完成，并保持了较高的最大伪峰和真实峰值差．由于解决了阵元大间距的问题，这种算法为今后针对伪峰抑制的平面阵天线设计目标提供了一种新的思路．

该算法的缺陷是对二维入射角来波估计采用虚拟阵列方法需要进行的转换矩阵运算比较复杂．

［1］Wax M，Sheinvald J. Direction finding of coherent signals via spatial smoothing for uniform circular array[J].IEEE Transactions on Antennas and Propagation，1994，42(5)：613-620.

［2］金荣洪，耿军平，范 瑜. 无线通信中的智能天线[M].北京：北京邮电大学出版社，2006.

Jin Ronghong，Geng Junping，Fan Yu.Smart Antenna Technologies in Wireless System[M]. Beijing：Beijing University of Posts and Telecommunications Press，2006(in Chinese).

［3］陈 辉. 非均匀线阵的模糊问题及方位估计[J]. 空军雷达学院学报，1999，13(1)：7-10．

Chen Hui. Problems of ambiguity and direction finding with non-uniformly linear array[J].Journal of Air Force Radar Academy，1999，13(1)：7-10(in Chinese).

［4］Tan K C， Oh G L，Er M H. A study of uniqueness of steering vectors in array processing[J].Signal Process，1993，34(3)：245-256.

［5］Tan K C， Goh Z. A detailed derivation of arrays free of higher rank ambiguities[J].IEEE Trans on SP，1996，44(2)：351-359.

［6］王永良，陈 辉，彭应宁，等. 空间谱估计理论与算法[M]. 北京：清华大学出版社，2004.

Wang Yongliang， Chen Hui，Peng Yingning，et al.Theory and Algorithm About Spatial Spectrum Estimation[M].Beijing：Tsinghua University Press，2004(in Chinese).

［7］吕泽均. 均匀圆阵的测向模糊研究[J]. 电讯技术，2008，48(7)：24-28.

Lu˙ Zejun. Study on the direction finding ambiguities performance of planar antenna array based on differential geometry[J].Telecommunication Engineering，2008，48(7)：24-28(in Chinese).

［8］陶建武， 石要武， 常文秀. 基于均匀圆阵的信号二维方向角高精度估计[J]. 航空学报，2006，27(4)：687-691.

Tao Jianwu， Shi Yaowu，Chang Wenxiu. High-precision of 2D angle for signal with UCAs[J].Acta Aeronautica et Astronautica Sinica，2006，27(4)：687-691(in Chinese).

［9］李艳斌. 空间谱估计无模糊测向的天线阵设置[J]. 无线电工程，1998，28(6)：5-6.

Li Yanbin. The antenna configuration for the nonambiguity in DOA estimation[J].Radio Engineering of China，1998，28(6)：5-6(in Chinese).

［10］Kim Young-Soo，Kim Young-Su. Improved resolution capability via virtual expansion of array[J].Electronics Letters，1999，35(9)：1596 -1597.

［11］宋石磊，于振海，赵国庆. 虚拟阵列测向性能分析[J].长沙航空职业技术学院学报，2006，6(4)：49-52.

Song Shilei，Yu Zhenhai，Zhao Guoqing. The DOA estimates based on virtual array lateral performance[J].Changsha Aeronautical Vocational and Technical College Journal，2006，6(4)：49-52(in Chinese).

［12］Wang Yongliang， Chen Hui. An effective DOA method via virtual array transformation[J].Science in China(Series E)：Technological Sciences，2001，44(1)：75-82.