倾斜转子-滑动轴承系统周期解稳定性研究
2011-06-05刘占生钱大帅孙立权
刘占生,钱大帅,孙立权
(哈尔滨工业大学 能源科学与工程学院,哈尔滨 150001)
转子-滑动轴承系统通常设计成卧式或者立式布置,相关分析和研究也都是针对这两种转子形式来进行的。但是在特殊情况下,转子-滑动轴承系统的轴线可能偏离设计和安装时的水平、竖直方向,成为倾斜转子。如船舶遭遇风浪发生摇荡运动时、船体破损倾斜时、航空器在加速爬升或作俯仰动作时,均可能出现转子轴线倾斜的状况。
目前对倾斜转子-轴承系统稳定性的专门研究还很少。关于转子轴线方向不同引起的稳定性差异问题多见于立式和卧式转子的对比研究,研究结论说明立式转子的径向载荷比较小,对振动较为敏感,稳定性比较差[1-3],可见滑动轴承径向载荷是影响滑动轴承性能和轴系稳定性的重要因素。Muszynska采用切向环流理论解释了径向载荷影响轴承性能的机理,认为当轴承径向载荷较小时,转子偏心较小,轴承间隙内的润滑油流动以环向流动为主,随着轴承载荷的增大,偏心量增大,润滑油轴向流动成分增加,甚至以轴向流动为主,油膜涡动和油膜振荡现象不容易发生,转子稳定性更好[4]。在转子从卧式、立式到倾斜状态的变化过程中,滑动轴承的径向载荷和润滑油流动状况将改变,转子-滑动轴承系统的稳定性也会受到影响。
由于转子轴线倾斜往往发生在工作环境恶劣或特殊工况下,对倾斜转子稳定性的研究就显得十分有必要。本文将对不同倾斜角工况下转子-滑动轴承系统的周期解稳定性开展仿真分析,并利用倾斜转子实验台进行实验研究,给出倾斜工况下转子的稳定性规律,为轴系的设计和应用提供理论依据。
1 倾斜转子-轴承系统及动力学方程
本文所研究的倾斜转子系统来源于Bently RK4实验台,如图1所示。轴线与水平方向的夹角为θ,支承1为滚动止推轴承,支承2为圆柱瓦滑动轴承。
采用有限元法对倾斜转子进行建模。使用两节点欧拉梁单元对转子进行离散化,整个转子共划分为10个节点,每个单元节点考虑弯曲振动的四个自由度。轮盘作为集中质量处理,此集中质量具有质量和转动惯量,在分析时考虑轮盘在旋转时的陀螺力矩。滚动轴承和滑动轴承处选为节点。
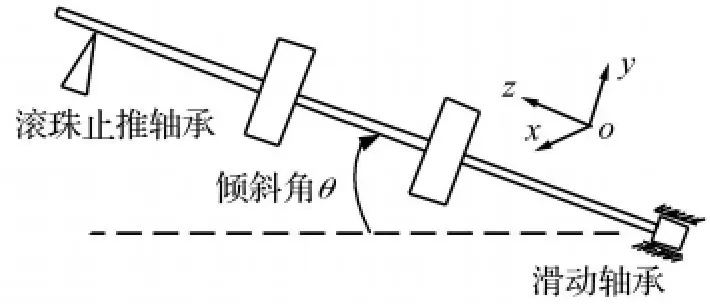
图1 倾斜转子-轴承系统简图Fig.1 Inclined rotor-bearing system
为了着重分析滑动轴承引发的转子周期解稳定性问题,将滚动轴承的支承作用简化处理,根据实验测得的静态主刚度系数,给出滚动轴承支承力:
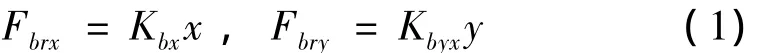
式中:x,y分别为两个坐标方向上的位移,Kbx,Kby是 x,y方向上的主刚度系数。在仿真时,此刚度系数和支承力不随转速和倾斜角度改变。
滑动轴承的油膜力采用基于短轴承假设的Capone模型[5],如式(2)~式(6)所示。
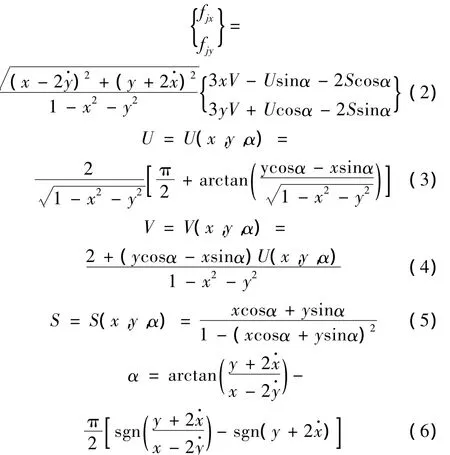
其中,fjx,fjy是两个方向上的油膜力,x,y是两个方向上的位移,是两个方向上的速度,α是滑动轴承偏位角,sgn(·)是符号函数。
径向载荷对滑动轴承的动力特性影响较大,因此转子重力是倾斜转子动力学特性研究中不可忽略的因素。在其他条件不变的情况下,转子倾斜引起的最主要变化应该是重力提供的滑动轴承径向载荷不同。针对轴承间隙内流动状态和油膜力的分析比较复杂,需要根据流体润滑理论求解雷诺方程。为了简化分析,仅考虑倾斜角度变化引起的轴承载荷的影响,建模时,认为沿轴线方向的转子重力分量对滑动轴承特性没有影响,仅考虑沿径向方向的重力分量。随着转子倾斜角度不同,滑动轴承受到的径向载荷发生变化,油膜力特性及转子的振动和稳定性也随之改变。
建立转子轴承系统的动力学方程为:
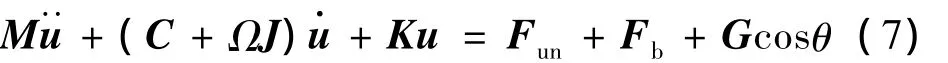
其中:M,C,J,K分别为系统的质量矩阵、阻尼矩阵、陀螺力矩矩阵和刚度矩阵,Ω是转子转速,Fun,Fb,G分别为不平衡力向量、轴承支承力向量和重力向量,u是位移向量。
仿真时采用的轴承直径为25mm,轴承间隙为140μm,轴承长度为25mm,油膜粘度为0.022 Pa·s,滚动轴承两个方向上的主刚度均取为1.5×107N/m。采用Newmark方法对方程(2)进行求解,可以得到转子-轴承系统各种状态下的动力学响应,求解时取Newmark的算法参数 β =0.5,γ =0.25。
2 不同倾角状态下转子-轴承系统的周期解稳定性
滑动轴承引发转子系统的周期解失稳的主要表现是油膜涡动和油膜振荡现象,这两种运动是转子周期运动出现分岔、进入多周期、概周期运动的体现。在分析过程中,通过分岔图和频谱分析可以清晰地判断出周期解的失稳。通过比较油膜涡动和油膜震荡的出现规律以及持续范围可以分析倾斜状态对转子轴承系统稳定性的影响。
倾斜转子动力学响应的典型仿真结果如图2和图3。图2是倾角为60°时转子-轴承系统滑动轴承处节点的三维谱图,图3是该节点的分岔图。油膜涡动从3850 r/min开始出现,振动响应的频率成分为0.485倍频,转子由周期运动直接进入分岔。油膜振荡的锁频现象出现于4350 r/min,稍低于第一阶临界转速的两倍。转子油膜振荡持续到7850 r/min时结束,转子重新进入周期运动,此时转子工作在第二稳定区。第二稳定区是有实际工程意义的,已经有实际转子系统工作在第二稳定区的实例[1]。第二稳定区持续到14200 r/min,从14200 r/min以后转子再次出现涡动现象,转子进入第二失稳区,第二失稳区内的涡动是“半频涡动”。
当转子处于不同的倾斜角度时,转子响应表现出来的特征基本一致,升速过程中稳定工作区和失稳区交替出现,包括发生“油膜涡动+油膜振荡”的第一失稳区、发生“半频涡动”的第二失稳区,如果计算转速足够高,还会出现第三、第四失稳区。所不同的是,当转子的倾斜角度改变,各个失稳区的失稳阈速和宽度发生改变。
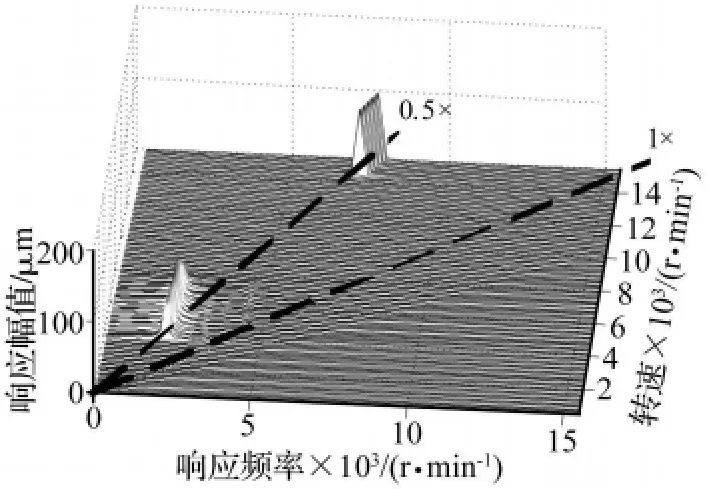
图2 倾斜转子响应三维谱图(θ=60°)Fig.2 Waterfall of inclined rotorbearing system(θ=60°)
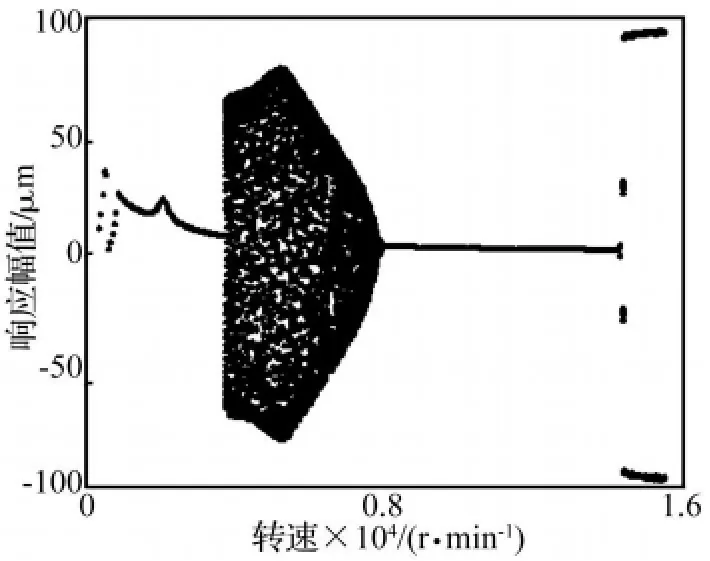
图3 倾斜转子分岔图(θ=60°)Fig.3 Bifurcation graph of inclined rotorbearing system(θ=60°)
图4是不同倾斜角工况下转子升速曲线,给出了第一失稳区的对比情况。随着倾斜角度的增加,第一失稳区的失稳阈速逐渐减小,从卧式布置时的4250 r/min减小到立式布置时的2700 r/min。当倾斜角度较小(0°~40°)时,失稳阈速随倾斜角变化幅度较小,当倾斜角在50°~80°之间时,失稳阈速变化幅度较大,而转子倾斜角为80°和90°时的失稳阈速比较接近。当转子立式布置时,低速(600 r/min)时就出现涡动,至1300 r/min消失,失稳阈速(2700 r/min)已经比较靠近一阶临界转速,说明立式转子稳定性较差。
在不同倾斜工况下,转子的一阶临界转速均为2200 r/min,这是因为所研究的转子是细长柔性转子,轴的刚度小于支承刚度,在倾斜状态改变时,支承状态的变化对转子第一阶临界转速影响很小。
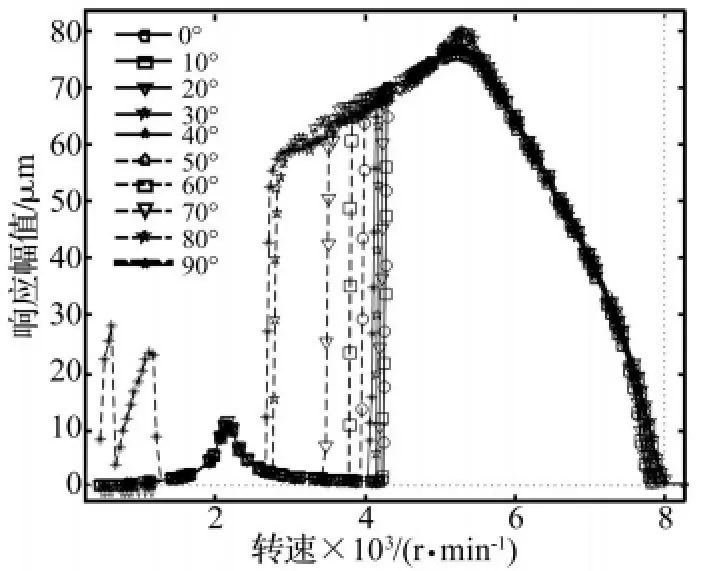
图4 不同倾斜角工况下转子升速曲线Fig.4 Speed-rising curve of rotor with different inclination angles
从图4中还可以看出,第一失稳区的上边界随倾斜角度增加而增加,但变化幅度不大,第一失稳区宽度的增加主要由失稳阈速的减小引起。实际上,第二和第三失稳区的规律也基本是这样,如图5所示。可以看出,转子倾斜角度的变化对失稳区下边界的影响较大,而上边界受影响较小。随着转子倾斜角的增加,转子-轴承系统的稳定性不断变差。倾斜角度较小时,在所研究转速范围内存在三个稳定区,而当倾角大于50°,转子仅存在两个稳定区,第二失稳区和第三失稳区已经连为一体。文献[6,7]中关于立式和卧式转子失稳区域和失稳边界的研究结论与此结果是一致的。
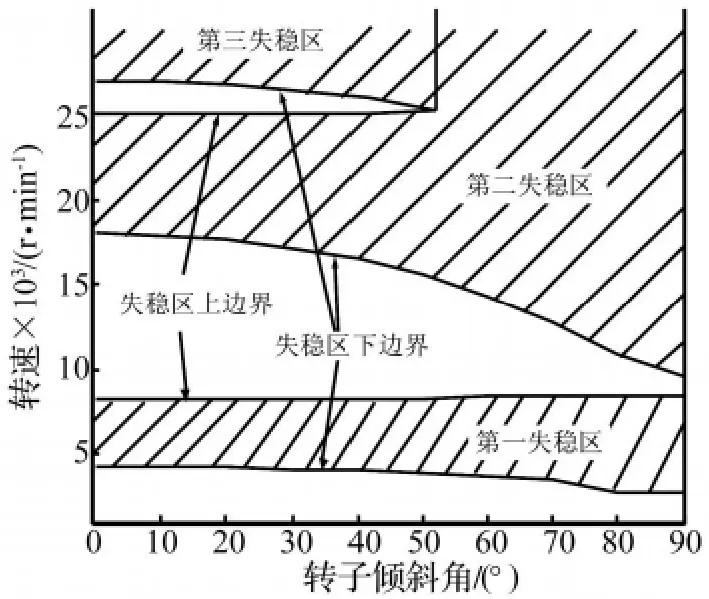
图5 倾斜转子失稳区域示意图Fig.5 Unstable area of inclined rotor
3 实验研究
倾斜转子-轴承系统实验台如图6所示。Bently RK4实验轴系安装在可旋转的基础上,基础的倾斜角度可选从0°至 90°之间间隔为10°的任一角度。基础依靠螺栓紧固在支架上,在紧固状态下,基础和支承结构的第一阶固有频率约为214Hz,在转子的升降速范围内可避免共振。实验中所用圆柱瓦滑动轴承采用端泄方式回油,通过油泵供油。

图6 倾斜转子实验台Fig.6 Test rig of inclined rotor
在不同倾斜角度工况下,进行了转子升速实验,部分轴承参数和工况条件如表1所示。出于安全原因,转子出现失稳后短时间运行后即降速停机,因此实验结果仅描述了第一失稳区的前半部分。在升速实验过程中,以转子出现油膜涡动或油膜振荡为失稳现象的开始,即失稳阈速。综合利用转子振动的频谱图、轴心轨迹图和分岔图就可以判断转子是否发生分岔和油膜涡动,即周期解是否失稳。

表1 实验轴承和工况参数Tab.1 Bearing parameters and operating conditions in experiments
实验过程中,不同倾斜工况下转子的第一阶临界转速均在在2250 r/min左右,与仿真结果吻合较好。从转子升速曲线可以看出,随着倾斜角的增加,转子失稳阈速不断减小。卧式布置时转子失稳阈速为4140 r/min,倾斜角度为30°时失稳阈速为 3570 r/min,70°时失稳阈速为3070 r/min,而立式布置时的失稳阈速为2880 r/min,非常靠近临界转速区,与仿真结果十分吻合。转子第一失稳阈速随转子倾斜角变化的曲线如图8所示,由图可以看出,仿真和实验研究结果规律基本一致,说明在进行动力学建模和仿真研究时,仅考虑倾斜工况引起的滑动轴承径向载荷变化是可行的。
但需要注意的是,仿真和实验结果仍然存在一些差别。例如仿真研究时转子振动从小幅值(小于20μm)的周期运动到较大幅值(大于80μm)油膜涡动或振荡的转变一般是较短时间内完成的,而实验中转子失稳区从小幅值油膜涡动开始出现到幅值迅速增大并非总是在较短时间内完成,小幅值油膜涡动往往会随着转速的升高持续一段时间,而后才迅速增大进入大幅值涡动区。从图7可以看出,实验升速曲线中,仅当转子水平布置以及倾斜角为10°时,转子失稳区涡动幅值才是出现后迅速增大的,这也说明了径向载荷对油膜涡动和振荡的抑制作用。另外,倾斜角为70°和80°时的升速曲线非常接近,失稳阈速差别也较小,在仿真结果中二者差别较大。仿真和实验结果的差别来源于仿真建模时的简化和实验误差,因此需要对倾斜状态下轴承间隙内润滑油流动特性做更合理的假设和分析,给出更准确的油膜特性,来更好地进行倾斜转子稳定性研究。
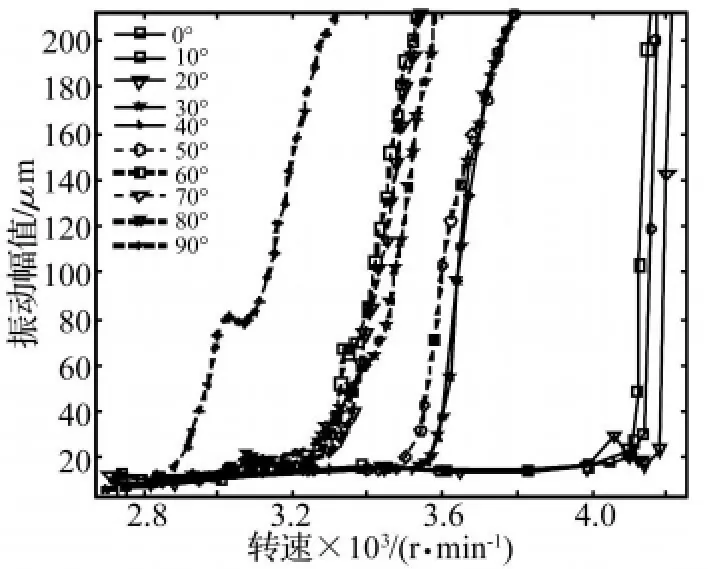
图7 倾斜转子升速实验曲线Fig.7 Experimental rise up curve of inclined rotor
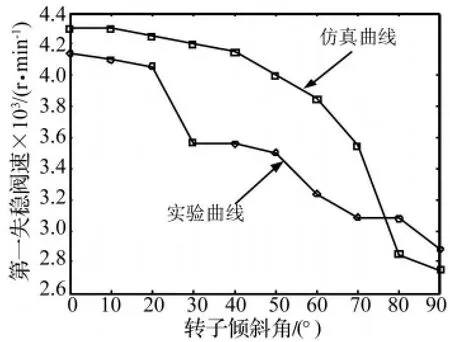
图8 失稳转速随转子倾斜角变化曲线Fig.8 Change of the first unstable threshold with inclined angle
4 结论
针对倾斜转子的周期解稳定性问题,考虑不同倾斜状态下滑动轴承径向载荷的变化,仿真分析了转子-滑动轴承系统的周期解稳定性,并进行了实验研究。仿真结果表明,不同倾斜角工况下转子的振动特征基本一致,但周期解的失稳阈速和失稳区宽度各不相同。转子倾斜角的增加会使转子周期解稳定性变差,使失稳阈速减小,失稳区宽度增大,但对失稳区上边界影响不大,失稳区宽度变化主要由失稳阈速减小引起。倾斜转子的升速实验结果验证了周期解稳定性随倾斜角变化的规律,说明本文在动力学建模时的简化处理是可行的,但需要做进一步的研究。
[1]彭超英,朱 均,陈瑞琪.立式弹性支承滑动轴承系统的上稳定区理论[J].振动工程学报,1996,9(4):358-365.
[2]何重辉,吴文英,陈瑞琪.滑动轴承中立式转子油膜稳定性的研究[J].纺织高校基础科学学报,2001,14(1):23-26.
[3]De Castroa H F,Cavalcaa K L,Nordmann R.Whirl and Whip Instabilities in Rotor-Bearing System Considering a Nonlinear Force Model[J].Journal of Sound and Vibration,2008,317(1):273-293.
[4]Muszynska A.Rotordynamics[M].New York,CRC Taylor&Francis Group,2005.
[5]Copone G.An Analytical Description of Fluid Dynamic Force Field in Cylindrical Journal Bearing[J].L’Energia Elettrica,1991,(3):105 -110.
[6]郭增林,杨益华.滑动轴承转子系统多稳定区形态特性研究[J].机械强度,2001,23(2):138-140.
[7]Guo Z L,Kirk R G.Instability boundary for rotor-hydrodynamic bearing systems,part 2:rotor with external flexible damped support[J].Journal of Vibration and Acoustics,2003,125(4):423-426.
