一些包含 Khatri－Rao积的矩阵不等式

任林源

（西安工业大学 数理系，陕西西安 710032）

一些包含 Khatri－Rao积的矩阵不等式

任林源

（西安工业大学 数理系，陕西西安 710032）

利用 Styan和 Liu的相关结果，主要研究了分块和非分块矩阵的 Khatri－Rao积，Khatri－Rao和与 Hadamard积的矩阵不等式，得到一些半正定矩阵和非奇异 Hermitian矩阵含有 Ktracy－Rao积等的矩阵不等式。所得含有 Khatri－Rao积的矩阵不等式可用于其它矩阵不等式方向的研究。

矩阵不等式；半正定矩阵；Hadamard积；Khatri－Rao积；Tracy－Singh积；Kronecker积

矩阵的Kronecker积在控制论、系统理论和最优化理论以及矩阵的Hadamard积在统计学的多元分析中，都是相 当 有 用 的［1－9］。我 们知道，矩 阵 的Khatri－Rao积是矩阵 Hadamard积的推广，Hadamard积和矩阵的普通积不依赖于 A和 B的分块形式，矩阵的 Tracy－Singh积、Khatri－Rao积通常依赖于矩阵 A和 B的分块形式，但矩阵块 Kronecker积，块Hadamard积，块Khatri－Rao积只与 B的分块有关［7，8］。设 Cm×n表示 m×n复矩阵，H（m）为 m ×m阶 Hermitian矩阵集，设 AH表示 A的共轭转置，A＋为A的Moore－Penrose逆，A0＝AA＋是 A到其列空间上的正交投影算子，A（α，β）是 A∈Cm×n的子矩阵，矩阵的行表示为 α⊂〈m〉＝ {1，2，3，...，m}，列表示为β⊂〈n〉＝{1，2，...，n}。特别的，有A（α， α）＝A（α）。如果矩阵 A是 Hermitian并且非负的，那么写作为A≥0（A＞0）。在Lǒwner偏序意义下，A≥B即为 A－B≥0。并且当 A≥0时，用A1／2表示 A的方根。

定义［6］设 A＝（aij）∈Cm×n，B＝（bij）∈Cm×n，B＝（bij）∈Cp×q，则 A⊗B＝（aijB）ijκ∈Cmp×nq被 定 义为分块矩阵 A，B的Kronecker积。

定义 1［6］设A＝（aij），B＝（bij）∈Cm×n，则定义 Hadamard积为 A·B＝（aijbij）ij＝B·A∈Cm×n

定义 2［7，8］设 A＝（Aij）∈Cm×n，其中 Aij是 A的第 ij子矩阵块，阶为 mi×nj，B＝（Bkl）∈Cp×q，Bkl是 B的第 kl子矩阵块，阶为pk×ql，并且有，则矩阵 A，B的 Tracy－Singh积定义为

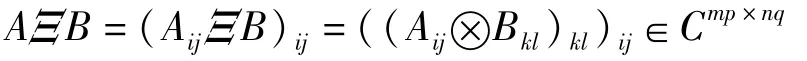
其中Aij⊗Bkl是 AΞB的第 kl子矩阵块，阶为 mipk×。

定义 3［7，8］设 A＝（Aij）∈Cm×n，B＝（Bij）∈Cp×q分别分块为 Aij是 A的第 ij子矩阵块，阶为 mi×

nj，Bij是 B的第ij子矩阵块，阶为，则矩阵A，B的 Khatri－ Rao积定义为

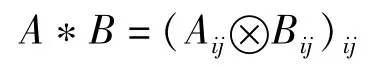
定义 4［7，8］设 A＝（Aij）∈Mm，B＝（Bij）∈Mn如下：Aij，Bij是第ij块，其阶分别是 mi×mi，nk×nk，，则矩阵 A，B的Khatri－Rao和定义为A∞B＝A*In＋Im*B∈MM，N，其中 M＝diag（Im1，...，Imr）。

引 理 1［9，10］

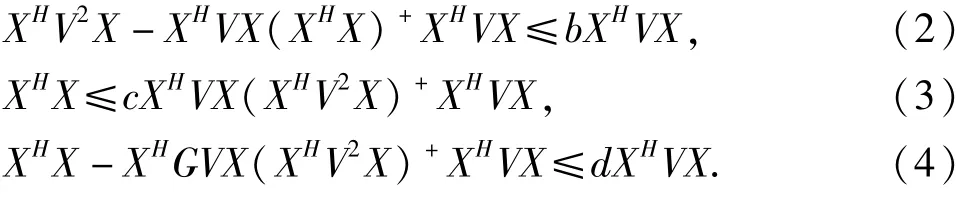
其中 V≥0，X＝V0X，a＝c＝（λ＋μ）2／（4λμ），b＝和 μ分别是矩阵V的最大和最小特征值。

引理 2［5，11］设 A，B，C，D是具有合适分块的矩阵，则

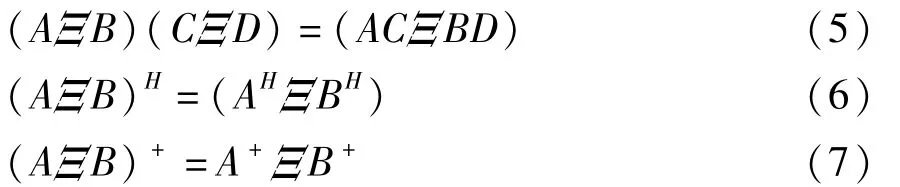
如果

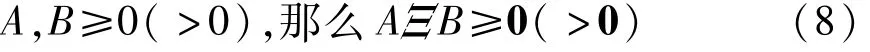
其中 Z是元素为 0，1的选择矩阵，满足 ZHZ＝I，式（9）成立当且仅当A，B都是方阵.

定理1 设A∈H（m），B∈H（p）是非负分块矩阵，α⊂〈mp〉由式（9）和式（10）通过Z确定，并且 α′＝〈mp〉＼α，如果 A＞0，B＞0，a＝c＝（λ＋μ）2／，λ和 μ分别是V的最大和最小特征值.并且分块如式（1），那么

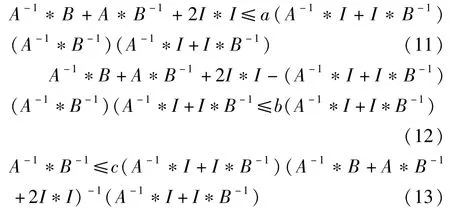
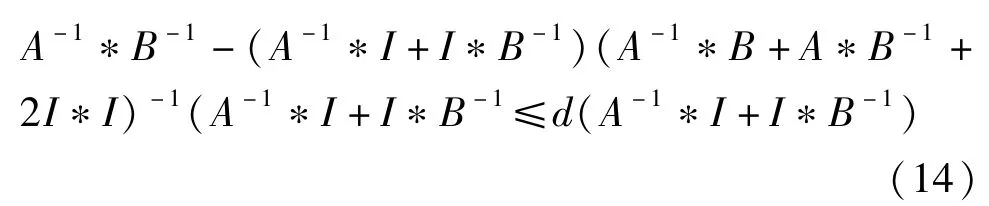
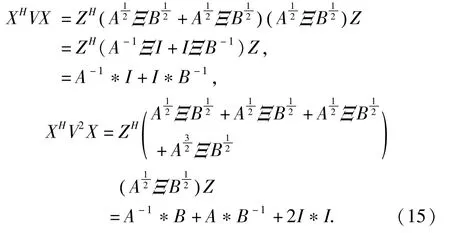
那么根据式（1）可得式（11），同理由式（2），（3），（4）可得式（12），（13），（14）。

定理2 设A∈H（m），B∈H（P）是非奇异方阵，α⊂〈mp〉，α′＝〈mp〉／α，如果（AΞB）－1（α′）＞0，则A *B可逆，并且（A*B）（A∞B）－1（A*B）≤A∞B.

证明 设 Q＝AΞB，M＝AΞI＋IΞB，那么

Q（α）＝A*B，M（α）－1＝（A*I＋I*B）－1，那么由推 论1［11］可 得

Q（α）H（AB）－1Q（α）≤（QHM－1Q）（α），即得到（A *B）（A∞B）－1（A*B）≤A∞B.

注意到对任意正实数 x有 x＋x－1≥2，所以对任意正定矩阵 M有M＋M －1≥2I，设 M＝AB－1，所以有AB－1＋A－1B≥2I，即有 A*B－1＋A－1*B≥2I，令 B＝A－1，那么有 A*A－1＋A－1*A≥2I.

定理3 设非奇异阵A∈H（m），B∈H（P），α⊂

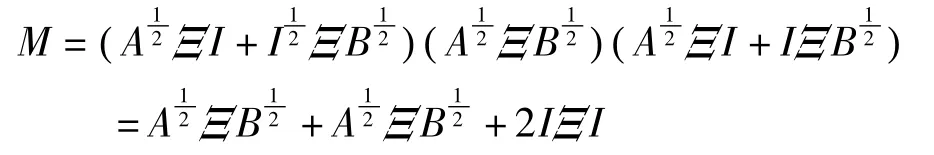
那么由推论 1［11］可得。

如果设 A＝（aij），B＝（bij）∈Mn，则定义 AΔB＝A·I＋I·B为A与B的Hadarmad和［14］。

设Q＝A⊕B＝A⊗I＋I⊗B，M＝A⊗B，

则

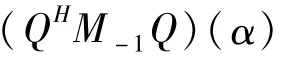
Q（α）＝A·I＋I·B，M（α）－1＝（A·B）－1，那么由Q（（α）HM（α）－1Q（α）≤（QHM－1Q）（α）可得

那么可以得到推论

（AΔB）（A·B）－1（AΔB）≤A·B－1＋A－1·B＋2I.

定理4 设 A∈Cn×m，并且 k∈［－1，1］，那么

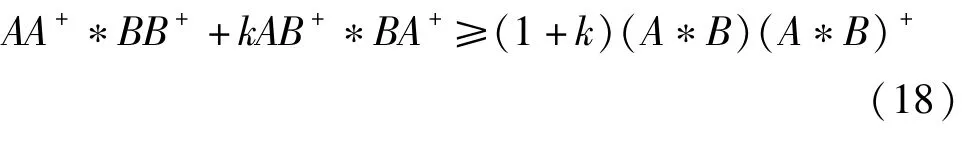
令 k＝2αβ／（α2＋β2），显然有式（18）。

当k＝0时，有AA＋*BB＋≥（A*B）（A*B）＋是AA＋·BB＋≥（A·B）（A·B）＋［12］的Hadamard积Khatri－Rao积推广；

当k＝1时，有AA＋*BB＋＋AB＋*BA＋≥2（A*B）（A*B）＋；

当 k＝－1时，有 AA＋*BB＋≥AB＋*BA＋.

［1］Tauber S.An application of the Hadamard product to air pollution［J］.Appl Math Comput，1978（4）：167－176.

［2］Killicman A，Zhour Z A.Improvements on geometricmeans related to the Tracy－Singh product of positive matrices［J］.Matematika，2005（21）：49－65.

［3］Ding F，Chen T.Iterative least－squares solutions of Coupled Sylvester matrix equations［J］.Syet Control Lett，2005（54）：95－107.

［4］Kilicman A，Zhour Z A.Kronecker operationalmatrices for fractional calculus and some appliacation［J］.Appl Math Comput，2007，187（1）：250－265.

［5］Cao CG，Zhang X，Yang ZP.Some inequalities for the Khatri－Rao product ofmatries［J］.Electron JLinear Algebra，2002（9）：276－281.

［6］Liu S.Several inequalities invoving khatri－Rao products of positive semi－defintematrices［J］.Linear Algebra Appl，2002，345：175－186.

［7］Liu S.Mtrix results on the Khatri－Rao and Tracy－Singh products［J］.Linear Algebra Appl，1999，289：267－277.

［8］Tracy D S.Balanced partitionedmatrices and their kronecker products［J］.Compute Statist Data Annl，1999（10）：315－323.

［9］Styan G PH.On some inequalities associated with ordinary least squares and the Kantorovich inequality［J］.Acta Uinv Tampere Ser A，1983（153）：158－166.

［10］Liu S，Polasek W，Nevdecker H.Equality conditions for matrix Kantorovich－type inequalities［J］.J Maty Anal Appl，1997，212：517－528.

［11］Liu S，Hadamard G，Khatri R.Kronecker and othermatrix products［J］.Int J Inform Syst Sci，2008（4）：160－177.

［12］George Visick.A quantitative version of the observation that the Hadamard product is a principal submatrix of the kronecher product［J］.Linear algebra Appl，2000，304：45－68.

［13］Horn R A，Mathias R.Cauchy－Schwarz inequalities associated with positive semidefinitematrices［J］.Linear algebra Appl，1990，142：63－82.

［14］Zhour Z.A，kilicman A.Some new connections between matrix products for partitioned and non－partitioned matrices［J］.Computers and Mathematics with Applications，2007，54：763－784.

［责任编辑 贺小林］

Some M atrix Inequalities Involving the Khatri－Rao Product

REN Lin－Yuan
（Department of Mathematics and Physics，Xi an Technological University，Xi an 710032，China）

Using the results provided by Styan and S.Liu，this paper is concerned with the inequality ofmatrix product for portioned and non－partitioned matrices，which involving the Khatri－Rao product，Khatri－Rao sum，and Hadamard product.Several product inequalities are obtained in the positive semi－definte matrix and in the non－singular Hermitian matrix case.It is easy to apply the result of inequalities involving the Khatr－Rao prouduct to the research in other fields.

matrix inequality；postive semi－definematrix；Hadamard product；Khatri－Rao product；Tracy－Singh product；

分类：O151.21

A

1004-602X（2011）01-0001-03

2011 -03 -10

陕西省教育厅科研计划项目（09JK494）；校长科研基金项目（XAGDXJJ0930）

任林源（1971—），男，陕西榆林人，西安工业大学讲师，博士。

Kronecker product