阴影衰落环境下无线传感网络的概率覆盖研究

刘 益 ，王 东 ，胡楚然 ,谢小婷

（1.湖南人文科技学院 计算机系，湖南 娄底417000；2.湖南大学 计算机与通信学院，湖南 长沙410082）

无线传感器网络由大量传感器节点组成，各节点通过无线链路与邻居节点保持通信[1]，具有易于组网、不受固定网络的约束等优点，现已被广泛应用于各个领域。由于传感器节点所带电池能量非常有限，所以,如何选择最少的工作节点数目使网络监测区域达到所需的覆盖质量成为无线传感器网络节点配置中的一个重要问题。

覆盖质量作为衡量网络服务质量的标准之一，根据不同的传感网络应用，有不同的度量方法。通常的度量方法是覆盖率，即至少被一个传感器节点探测的几何区域与整个网络监测区域的面积之比。许多学者对无线传感器网络的覆盖问题进行了研究，其中大多采用布尔传感模型[1]，即在任一传感器探测范围内的事件都能被完全可靠地感知，否则完全无法被感知。参考文献[1]在考虑覆盖问题时引入了一般传感模型，即传感器输出信号强度随其与被探测物体之间距离的增加而减小。在此基础上，参考文献[2]等提出了能更准确定义覆盖能力的概率感知模型,指出:在基于无线电波感知的传感器网络中，除距离外，传感信号还受到周围障碍物、无线电干扰等因素的影响，使传感器对其周围事物的探测并非是确定的(事物要么能被探测到，要么不能被探测到)，而是服从一定分布的概率。此外，参考文献[3]充分利用布尔感知模型中被忽略但实际有效的少量能量并进行聚合，提出了协作感知模型，即被监测区域中的任意点能否被探测到，并不是单独地由某一个传感器节点决定，而是由其周围多个节点共同感知的结果。

然而，在无线传感器的具体的实际应用中，无线电干扰和各个节点间的能量聚合是存在的，这种情况在无线传感器网络的覆盖问题研究中还没有引起足够的关注和重视。本文较全面考虑影响覆盖情况的各个因素，采用合理的覆盖质量度量方法来建立覆盖模型。

1 基于概率的协作感知覆盖模型的建立

1.1 单个传感器节点的概率感知模型

自由空间环境下其能量损耗仅与信号的传播距离有关，称为基本损耗[4]。但是，在基于电波传感的网络中，信号在传输过程中会不可避免地遇到各种障碍物阻挡和其他电波的干扰，产生绕射现象，使信号强度绕中值上下波动，形成阴影衰落。此时，能量损耗为基本损耗与随机变量之和，且随机变量服从对数正态分布，满足[4]：

其中，r为传感器节点与被探测物之间的距离；Le(r)为距离为r时的能量损耗；η为路径损耗指数；Xσ是均值为0、标准偏差为δ的正态分布随机变量，即其概率密度函数为：

设衰落阈值为Lth(单位为 dB)，则：

由此可得出，当被探测物与传感器节点间的距离为r时，被探测到的概率为：

差函数表示为：

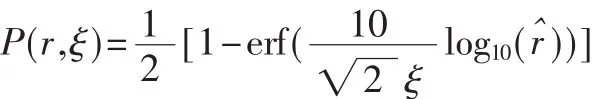
假设自由空间环境下，被探测事物和节点间的距离为r时，区域平均能量为Ea(r)=cr-η(c为常数)，则阴影衰落环境下，接收能量E(r)满足：

其中xσ是均值为 0、标准偏差为δ的正态分布随机变量。

对上式两边同时除以覆盖阈值对应的感知半径处的区域平均能量 Y=c(r0)-η，则：

从 上 式 可 以 看 出 ，10log10(E(r)/Y)是 以 10log10为均值，σ2为方差的正态分布。若传感信号要被节点正确接收，感知概率可表示为：

从上式可以看出，传感器对监测区域内任意点的探测概率是介于0和1之间的随机值，其值大小不仅与距离r＾有关，还与阴影衰落因子 ξ有关。

1.2 基于概率的协作感知

在实际无线传感网络中，对于被检测区域内任意点S，通常受到多个传感器节点(假设有N个)的共同探测，此时该点被协作感知的概率为：

其中Pi()为第i传感器节点Ni在 S处的探测概率。

引理1 阴影衰落环境下，网络监测区域内的任意被监测对象，其协作感知概率不小于任何单个传感器节点对它的感知概率。

证 明 ： 对 于 任 意 的 传 感 器 节 点Ni， 都 有 0≤≤1，则：

连乘得：

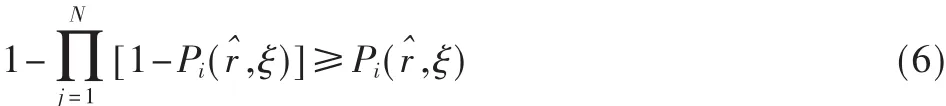
即S点的协作感知概率大于任何单个传感器节点对它的感知概率。

为了方便说明，现给出以下定义：

定义1 在自由空间环境下,称无线传感器节点的感知半径为物理感知半径。

定义2 在传感器周围,感知概率小于一定阈值Ppre的区域视为无法探测，此阈值称为传感器的覆盖精度。

定义3 在一定的阴影衰落环境下,对应于某一覆盖精度Ppre的传感器与被监测对象间的距离为R，由概率感知公式(3)可知，有:

解得：

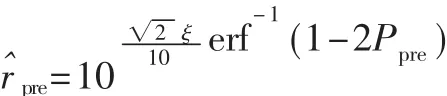
定义4 当某点周围的传感器节点对此点的协作探测概率大于某一预先设定阈值C0时，则此点称为有效探测点。

定义5 在基于概率的协作覆盖模型下,有效探测临界点与最邻近的传感器节点之间的距离称为协作感知半径。

定义6 网络中监控对象被网络中所有节点协作感知到的概率的最小值,叫做传感器网络的感知概率,记为CN，满足下式：

其中，C(,ξ)为监测区域中的任意点的协作感知概率。

使得：yi(ωTϕ(xi)+b) ≥1-ξi，ξi≥0,i=1,...,l，其中C为分类系数，ξi表示第i个向量的松弛因子。为了更高效地求解上述问题，使用拉格朗日乘子法可得到其对偶问题[13]：

定义7 在阴影衰落环境中,用覆盖质量来衡量无线传感器网络的覆盖性能，包括网络感知概率、覆盖精度以及网络覆盖率。

为了方便研究，本文采用如图1所示的正三角形拓扑结构的规则部署方法，研究在不同覆盖要求和质量下监测覆盖区域所需的节点数目。

图1 正三角形结构的网络配置

由Voronoi图的相关知识可知，网络中感知概率最小值为3条Voronoi线的交点处，本文称之为覆盖最弱点，如图1中的S。又由定义6可知传感器网络的感知概率即为S处的感知概率。下面分析S处的感知概率。

考虑与 S处最邻近的 3个传感器节点 1、2、3。

从图1可以直接看出，此3个传感器节点到S处的欧式距离相同，记为。由协作感知概率公式可知，S处的协作感知概率为：

由上式计算出：

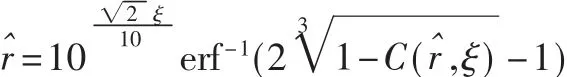
同样的方法，分析与S处最邻近的6个传感器节点(编号为1～6)。因为增加协作感知的传感器个数，导致协作感知概率增大，若保持最小感知概率不变，则S点与周围最邻近的3个节点间的距离变大，记为又由几何知识可知，节点 4、5、6与 S处的距离为易得 S点的协作感知概率为：

由于受到最大探测半径R(Ppre)的限制，上式还必须满足≥R(Ppre)的条件下才成立。基于此，下面给出协作感知半径取值的分类方法：

利用引理1可得定理1，求出协作覆盖感知模型中，覆盖以边长为A的正方形监测区域所需的最少节点数目。

定理1在阴影衰落环境下，当正方形网络监测区域的边长A远远大于传感器节点的协作感知半径时，以一定的感知概率CN覆盖网络区域所需的工作节点数目n应满足以下公式：

1.3 模型分析

(1)阴影衰落因子

由于误差函数在实数范围为增函数，根据复合函数单调性的判断方法和概率感知公式(3)，探测概率是关于阴影衰落因子 ξ的增函数，即当一定时，若 ξ1≤ξ2，则协作感知概率满足：

引理2在协作感知模型中，对于一定的最大探测半径和感知概率，协作感知半径是关于阴影衰落因子的单调递增函数。

综上所述，协作感知概率是关于阴影衰落因子的单调递增函数。证毕。

由定理1和引理2可得如下推论：

推论1在协作感知模型中，对于一定的最大探测半径和感知概率，覆盖整个网络监测区域所需的最少节点数目随阴影衰落因子的增大而减少。

(2)网络感知概率

由于反函数和原函数具有相同的单调性，且erf(x)为实数域上的增函数，所以erf-1(x)也为增函数。又因为f(CN)在[0,1]上为减函数，根据复合函数单调性的判断方法（相异为减）和式(7)，协作感知半径是关于网络感知概率CN的减函数。也就是说，网络感知概率越大，协作感知半径越小，覆盖监测区域所需的节点数目越少；网络感知概率越小，协作感知半径越大，覆盖监测区域所需的节点数目越多。

(3)覆盖精度

从协作感知半径取值的分类方法可以看出，当阴影衰落因子一定时，减小覆盖精度，则最大探测半径增多，使得网络中感知概率最小的点有可能被更多的节点感知，从而增大协作感知概率，即增大了网络感知概率。反之当网络感知概率一定时，随着覆盖精度的减小，协作感知半径增大，覆盖网络监测区域所需的最少节点数目减少。

2 实验仿真与分析

本实验采用Matlab7.1进行模拟仿真。假设传感器节点的物理感知半径为单位长度 1，监测区域为 50×50的正方形。为了减少边界效应，应增大节点部署范围，即在与监测区域同心的60×60的正方形中 （称之为外正方形，监测区域称为内正方形），按正三角形拓扑结构规则布点[1]。同时，把内正方形边长分为500等分。由于小网格的面积与单位面积相比非常小，所以当网格的中心点的协作感知概率大于覆盖阈值时，即认为该小网格被覆盖[6]。显然，被覆盖的小网格数目与总的小网格数目之比就是覆盖率。此外，阴影衰落环境下，考虑小网格是否被覆盖，与衰落因子产生相应的正态分布随机数x有关，若x-10ηlog10(r/r0)≥0则该小网格被覆盖，r0是节点的物理感知半径，r是网格中心点与节点的实际距离。为了更好地反映统计规律,所有结果都是100次实验的平均值。

图 2、图 3、图 4分别为不同阴影衰落因子、网络感知概率、覆盖精度下的覆盖率，可以看出：

(1)网络覆盖率随传感器节点与覆盖最弱点间距离的增大而减小；

(2)当节点与覆盖最弱点之间的距离等于协作感知半径的理论计算值时，网络覆盖率几乎为1。

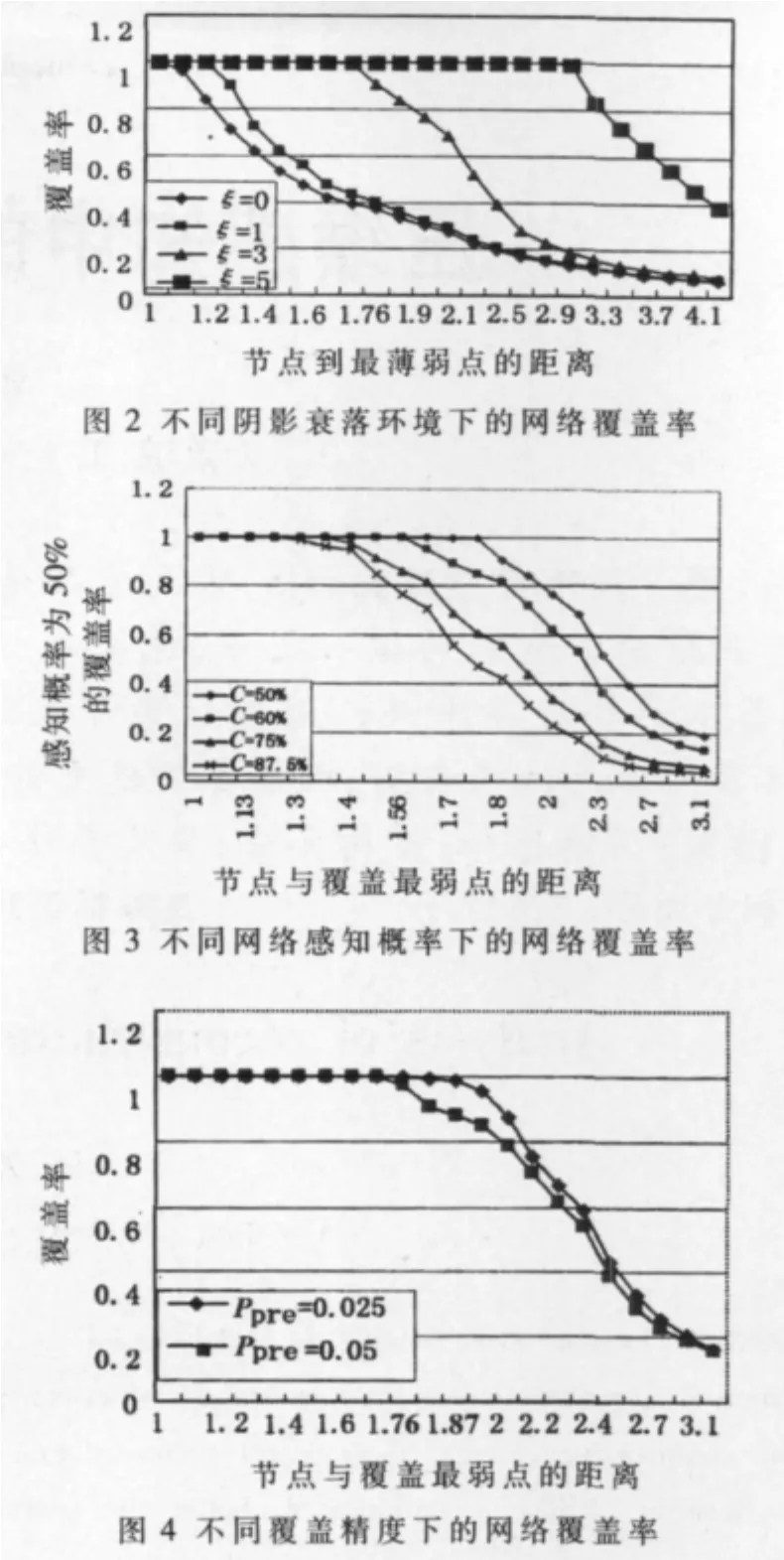
(3)节点到最薄弱点的距离随阴影衰落因子的增大而增大；随网络感知概率和覆盖精度的增大而减小。

因为本实验按正三角形拓扑结构规则布点，最少工作节点数目与节点到覆盖最弱点的距离呈负相关关系，由此可知，最少工作节点数目随阴影衰落因子的增大而减少，随网络感知概率和覆盖精度的增大而增大。

本文针对阴影衰落环境下无线传感器网络的覆盖问题，采用正三角形结构的部署节点，利用了单个节点的概率探测和多个节点间的协作探测特性，充分考虑阴影衰落因子、网络感知概率、覆盖精度对无线传感器网络覆盖的影响，提出了基于概率的协作感知覆盖模型，并推导出满足一定覆盖质量要求的协作感知半径和最少工作节点数目的计算公式。经分析和实验仿真可知，阴影衰落因子的增大，网络感知概率或覆盖精度的减小，都会导致协作感知半径的增大，从而减少最少工作节点数目，延长网络寿命。

[1]Liu Benyuan,TOWSLEY D.A study of the coverage of large-scale sensor networks:international conference on mobile Ad-hoc and sensor systems,2004[C].Massachusetts：IEEE，2004：475-483.

[2]BETTSTETTER C，ARTMANN C.Connectivity of wireless multihop networks in a shadow fading environmen[J].Wireless Networks，2003，11(5)：571-579.

[3]杨白薇，于宏毅，李宏.基于协作的无线传感器网络休眠调度算法[J].计算机应用研究，2008，25(3)：677-180.

[4]刘乃安.无线局域网—原理、技术与应用[M].西安：西安电子科技大学出版社，2004:32-39.

[5]ZHANG H,HOU J C.Maintaining sensing coverage and connectivity in large sensor networks[J].Ad Hoc&Sensor Networks,2005,1(3):89-124.

[6]WAMG B，Wang Wei，SRINIVASAN V,et al.Information coverage for wireless sensor networks[J].Communications Letters,2005，9(11)：967-969.