IOWAS算法的卫星分组策略研究

郭 婧，陆明泉，冯振明

（清华大学 电子工程系，北京100084）

全球卫星导航系统（GNSS）的基本功能是向具有适当接收设备的各类用户提供实时、准确、连续的三维位置、速度和时间信息，具有精度高、实时性强、作用范围广、全天候等优点。考虑到系统的各部分都存在出现异常情况的可能，还必须采取一定的机制来保证这些功能是可靠的，与此相对应的指标就是完好性。完好性是当系统不能可靠使用时及时向用户发出告警的能力，对于航空应用非常重要：一方面由于用户的航行速度很高，一旦发生异常情况将很快偏离航路；另一方面由于它关乎生命安全。

卫星导航系统有多种完好性监测或增强的方式，其中接收机自主完好性监测(RAIM)是在用户端独立实现的完好性监测方法，因其对故障反应迅速、实现简单等显著优点成为了一种基本的、必不可少的完好性监测方式。美国联邦航空局(FAA)规定，当GPS用作航空辅助导航设备时必须包含RAIM功能[1]。

早期的接收机自主完好性监测算法，大多使用GPS单星座单频点的卫星信号，并且基于单星故障的假设，设计目标是保证民用航空飞行中航路到非精密进近阶段的完好性。然而，随着GNSS的发展，未来的民用导航接收机将可以使用多星座多频点的卫星信号进行定位和导航。可见卫星数量大大增加，一方面能够改善卫星的几何布局，显著提高定位精度和完好性，另一方面也使得多星故障发生的概率增加，原本的单星故障假设不再能够满足更高级别的完好性要求。越来越多的RAIM算法开始考虑多星故障的问题，本人也提出了一种双星故障假设下的多星座RAIM算法——IOWAS[2],该算法基于对卫星进行分组和在定位域加权的基本思路，能够兼容任意多个卫星星座，充分利用全部的卫星信号，支持民航的垂直引导进近(APV)飞行阶段。然而算法中缺乏对卫星分组策略的探讨，从而无法获得更高的可用性。为了拓展IOWAS算法的使用范围，进一步提高算法在各飞行阶段的可用性，本文探讨了IOWAS算法中的卫星分组策略优化问题。

1 IOWAS算法

如图1所示,IOWAS算法首先将全部可见卫星分为三组，分别计算各组的最小二乘定位解x1、x2和x3，将三个定位解进行加权平均得到加权平均解xA作为最终的定位结果，其表达式如下所示：

图1 IOWAS算法原理示意图

其中，加权因子r1、r2和r3满足r1+r2+r3=1的条件。分组定位解xn(n=1,2,3)与加权平均解xA之间的间隔距离dn为三个检测统计量，根据最大允许的虚警概率，可以计算得到三个检测门限Dn。对于给定的最大允许漏检概率,可以得到每个分组定位解在无故障假设下的定位误差上限an。PLn=Dn+an，分别是假设第n个分组内无故障星时对应得到的保护级别。最终算法输出的保护级别PL=max(PL1，PL2，PL3)，这是基于 RAIM 算法中普遍采用的“最坏情况条件”准则 。

IOWAS算法的设计目标是保证APV飞行阶段的完好性，相对于水平方向的完好性，垂直方向的完好性通常更难保证，所以以下讨论只考虑垂直方向上的定位精度和完好性要求。垂向保护级别VPL的计算公式如下：

其中，VPLn是假设第n个分组的卫星不存在故障时得到的垂向保护级别,Dv,n表示垂直方向上的三个检测门限，av,n表示在假设第n个分组的卫星不存在故障时，定位解xn在一定置信度下的垂向定位误差上限,表达式如下：

其中，KFA是由虚警概率决定的参数，dPn是第n个分组的定位解xn和加权平均解xA之间距离的协方差矩阵，KMD是由漏检概率决定的参数，Pn是第n个分组的定位误差协方差矩阵。

IOWAS算法的核心问题是如何优化加权因子，使得在满足定位精度要求的前提下极小化VPL值,从而极大化算法的可用性，可以归纳为如下数学问题：

其中：σv为加权平均解 xA的垂向定位误差标准差，σv-max为各飞行阶段规定的95%垂向定位精度所对应的最大垂向定位误差标准差。在对完好性要求非常严格的APV飞行阶段，定位解的完好性通常比精度更难保证，所以算法以牺牲一定的定位精度为代价，换取了更高的可用性，这样的权衡是必要且合理的。

2 卫星分组策略优化

IOWAS算法可以通过优化卫星分组策略，进一步提高可用性。分析式(2)、式(3)、式(4)后可以看出，通过减小，即减小每个分组的垂向定位误差标准差，可以降低VPL，从而提高算法的可用性。因此，本文卫星分组的基本思想是使每个分组定位解都具有最佳的垂向定位精度，即每个分组内的卫星都具有最小的垂向精度因子（VDOP）。

2.1 精度因子（DOP）

DOP是将用户的位置和时偏误差与伪距误差相关联起来的几何因子，用来表征用户和可见卫星在空间几何分布的好坏。精度因子越小，几何分布越好，定位精度也就越高。

精度因子通常包括几何精度因子（GDOP）、位置精度因子（PDOP）、水平精度因子（HDOP）、垂向精度因子（VDOP）和时间精度因子（TDOP）5个参数，各参数的计算公式如下：

图2 不同时刻的DOP值分布曲线

其中，矩阵D=(HTH)-1，H是定位解算方程中的线性化关联矩阵，其每行的前三个元素分别为用户指向卫星的矢量与三个坐标轴的夹角余弦，第四个元素为1。由此可见，DOP值完全由用户与卫星间的几何分布决定。在计算DOP值时，应使用ENU坐标系，以方便表示水平方向和垂直方向上的定位精度。

通过仿真，给出一段时间内的各种精度因子数据。用户位置设为清华大学校园内的某已知位置，卫星位置采样了GPS 25星在24小时内的1 440个历元的位置信息，仰角遮蔽角设为5°。图2给出了不同时刻的GDOP、PDOP、HDOP和VDOP分布曲线，图3给出了对应的可见卫星数。

从图中可以看出，在绝大多数时间里，可见卫星数都在6颗或6颗以上。VDOP值通常比HDOP值大，平均HDOP值为 1.072 4，平均 VDOP值为 1.597 3，这也验证了卫星导航接收机的水平定位精度优于垂向定位精度。GDOP、PDOP和 VDOP随时间的变化趋势完全一致，因此，当希望每个分组内的卫星都具有最小的VDOP值时，即可以转化为使每个分组的卫星都具有最小的GDOP值,从而可以利用现有的很多针对GDOP的研究成果，探讨卫星的最佳分组策略。

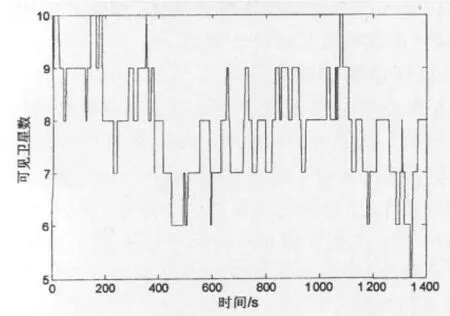
图3 可见卫星数

2.2 卫星分组策略

根据参考文献[3]中给出的结论，当若干颗卫星位于天顶位置，其他卫星均匀分布在仰角为遮蔽角的底圆圆周上时，卫星具有最佳分布，即对应最小的GDOP值。因此，卫星的最佳分布可以用位于天顶的卫星数来表示，表1给出了卫星具有最佳分布时，位于天顶的卫星个数与可见卫星总数之间的关系[3]。

表1 卫星最佳分布时位于天顶的卫星数和可见卫星总数的对应关系

受到卫星的实际运行轨道的限制，不可能真正存在若干颗卫星位于天顶，其他卫星均匀分布在仰角为遮蔽角的底圆圆周上的最佳分布，因此，可以用高仰角的卫星来代替位于天顶的卫星，并且使其他卫星的方位角尽量在0～360°之间均匀分布，即可获得与最佳分布相似的分布，从而得到较小的GDOP值。在IOWAS算法中，对卫星分组优化的基本策略是使每个分组内的卫星分布都尽量与最佳分布相似，从而使每个分组都获得尽量小的VDOP值。下面给出具体的卫星分组过程：

(1)计算所有可见卫星的仰角和方位角。

(2)将可见卫星总数除以3，确定每个分组的卫星数。如果余数为0，则每组卫星数相同；如果余数为1，则第三个分组的卫星数比其他组多一个；如果余数为2，则第二和第三组的卫星数相同，都比第一组多一个。

(3)查表得到每个分组的卫星数对应的位于天顶的卫星数 N1、N2、N3。

(4)根据每个分组的卫星数和位于天顶的卫星数，计算得到每个分组中剩余的卫星数L1，L2，L3。

(5)将所有卫星的仰角进行排序，选择其中仰角最大的(N1+N2+N3)颗卫星轮流分配给每组。仰角最大卫星的分配给第一组，第二大的分配给第二组，第三大的分配给第三组，以此类推，直到每个分组中得到的高仰角卫星个数分别达到N1、N2和N3。

(6)将剩余卫星的方位角进行排序，按从小到大的顺序轮流分配给每组。方位角最小的卫星分配给第一组，第二小的分配给第二组，第三小的分配给第三组，以此类推，直到每个分组中得到的卫星个数分别达到L1、L2和L3，从而使每个分组中除高仰角以外的剩余卫星的方位角都尽量在0～360°范围内均匀分布。

3 仿真分析

在这一节中，通过仿真来分析卫星分组策略优化对IOWAS算法性能的影响。在仿真中，卫星定位系统采用GPS 24星、Galileo 27星和 GLONASS 24星的三星座兼容方式，共采样1 440个历元的卫星位置 (24 h，一个/min)；用户位置遍历全球24个用户地点，它们取自于RTCA规定的 GPS“最小操作性能标准”[4]；仰角遮蔽角设为5°；伪距误差模型参见参考文献[5]。表2给出了国际民航组织(ICAO)对不同飞行阶段的垂向定位精度、告警限和可用性要求。

表2 各飞行阶段的导航性能要求

分别考察在双频定位模式和WAAS双频定位模式下卫星分组策略对IOWAS算法可用性的影响。仿真结果如图4所示。图中实线是简单按星座进行分组的IOWAS算法可用性曲线，虚线是使用了第2节中介绍的卫星分组策略之后的算法可用性曲线。可以看到，分组策略的优化可以进一步提高IOWAS算法的可用性，尤其是在垂向告警限比较小的时候，性能改善更为显著。

表3总结了IOWAS算法在不同飞行阶段的可用性。可以看出，在双频定位模式下，IOWAS算法无论采用哪种卫星分组策略，都只能支持一类垂直引导进近（APVI）和二类垂直引导进近（APV-II）两个飞行阶段，在一类精密进近（CAT-I）飞行阶段，分组策略的优化可以使IOWAS算法的可用性提高7.15%。在WAAS双频定位模式下，无论采用哪种卫星分组策略，IOWAS算法都能够支持APV-I、APV-II和 CAT-I三个飞行阶段，在每个飞行阶段，优化分组策略都能提高算法的可用性。

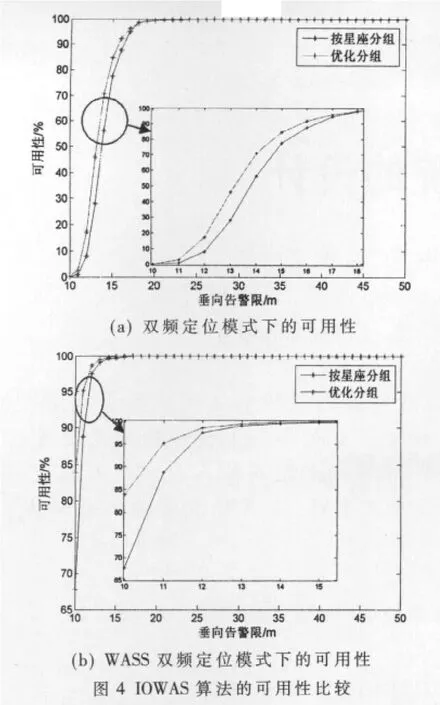
表3 IOWAS算法的可用性列表

本文探讨了IOWAS算法的卫星分组策略优化问题，通过分析各种精度因子参数之间的关系，并借鉴已有的针对GDOP最小时卫星最佳分布的研究成果，给出了优化的卫星分组策略：使每个分组内的卫星分布都尽量与最佳分布相似，从而使每个分组都获得尽量小的VDOP值。仿真结果表明，分组策略的优化可以进一步提高IOWAS算法的可用性，尤其是在垂向告警限比较小的时候，性能改善更为显著。使用优化卫星分组策略的IOWAS算法，在双频定位模式下，能够以极高的可用性支持APV-I、APV-II两个飞行阶段，并将按星座进行分组的IOWAS算法在CAT-I飞行阶段的可用性提高了7.15%。在WAAS双频定位模式下，IOWAS算法无论采用哪种卫星分组策略，都能以极高的可用性支持APVI、APV-II和 CAT-I三个飞行阶段。

[1]TSO-C129a.Airborne supplemental navigation equipment using the global positioning system（GPS）[S].FAA Aircraft Certification Service,Federal Aviation Administration,Washington D.C.,1996.

[2]郭婧，崔晓伟，陆明泉，等.支持垂直引导进近的多星座RAIM算法[J].清华大学学报（自然科学版），2011(2)：156-160.

[3]Zhang Miaoyan,Zhang Jun.A fast satellite selection algorithm:beyond four satellites[J].IEEE Journal of Selected Topics in Signal Processing,2009,3(5):740-747.

[4]Document RTCA/DO-208.Minimum operational performance standards for airborne supplemental navigation equipment using global positioning system(GPS)[S].USA:RTCA,1991.

[5]LEE Y,BRAFF R,FERNOW J,et al.GPS and galileo with RAIM or WAAS for vertically guided approaches[C]//Proc of ION GNSS 2005.Long Beach,CA,USA,2005:1801-1825.