不对称故障下双馈风力发电机转子变换器控制研究

宋平岗，喻 冲

(华东交通大学 电气学院，南昌 330013)

引言

随着全球经济的快速发展，人类对能源的需求与日剧增，而地球上常规能源有限，风能的开发利用已成为全球的共识。随着风电机组装机容量的增大，风电的并网对电网的影响越来越严重，因此须提高风电机组对电网故障的响应能力。

对于目前广泛采用的 DFIG而言，由于其发电机定子与电网直接相连接，因此其受电网影响比较大。文献[1]对电压不对称跌落下的电网的频率，相角和幅值的快速检测进行了研究，这是分析风电机组不对称运行的前提。文献[2～4]对不对称跌落下的风电机组进行了建模与分析，对变流器提出了四种控制方案，并得到不同控制方案下，正、负序转子电流的给定量。但是这些研究成果多重点研究电压发生小值跌落下的控制策略，而对大值跌落下的研究较少，而发生大值跌落时转子侧变换器的过流和过压更加明显。文献[5]对A相跌落20%的情况进行了仿真，但对Crowbar的控制方式未给出具体的分析。文献[6]对电网发生对称大值跌落下的转子侧Crowbar电路的控制策略进行了分析，而未对不对称跌落的控制策略进行分析。

本文重点研究电网电压不对称跌落下 DFIG转子侧变流器的控制策略，提出了一种抑制转子侧负序电流和并联Crowbar电路的控制策略。

1 不平衡电网电压下DFIG模型

为了对电网发生不对称电压跌落情况下 DFIG的暂态过程进行分析，首先建立 DFIG在不平衡电网电压下的数学模型，图1给出了两相静止αβ坐标，以同步转速ωs正向旋转的正序坐标dq+和以-ωs反向旋转的负序坐标dq-三者之间的矢量关系，由图1可得矢量关系式：

图1 αβ，dq+，dq-坐标之间的矢量关系

式中F可表示为电压，电流或磁链，指数上面的+、-表示正序、负序旋转参考坐标。

DFIG在两相旋转坐标系下的 T型等效电路图如图2所示。

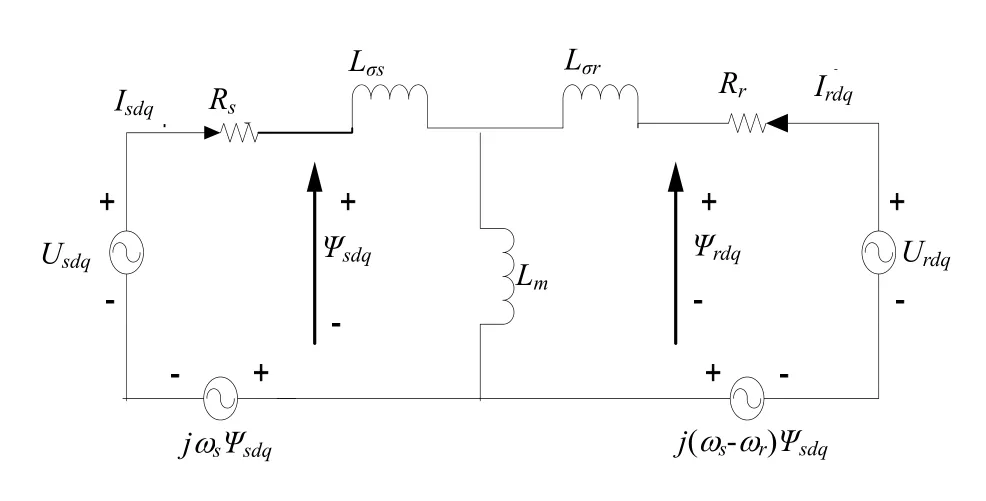
图2 DFIG的T型等效电路

由图2可得，其定子和转子的磁链和电压方程如下：

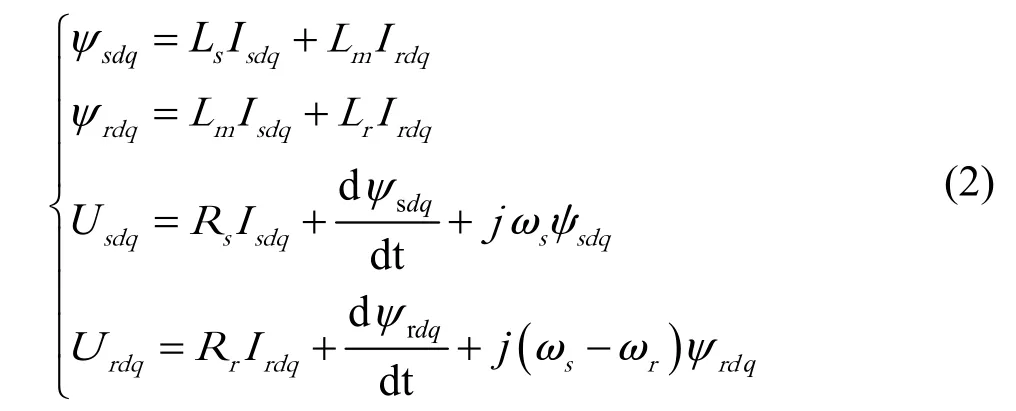
式中，Rs和Rr为定子和转子绕组的电阻值；Ls=Lσs+Lm和Lr=Lσr+Lm为定子和转子的自感；Lσs，Lσr，Lm分别为定转子漏感和定转子之间的互感；Isdq，Irdq为定转子电流；ωs为同步角速度；ωr为转子角速度；ωs-ωr为相对角速度。

由式(1)和图(1)可知，定转子电流，电压和磁链可表示为正序和负序分量的组合：

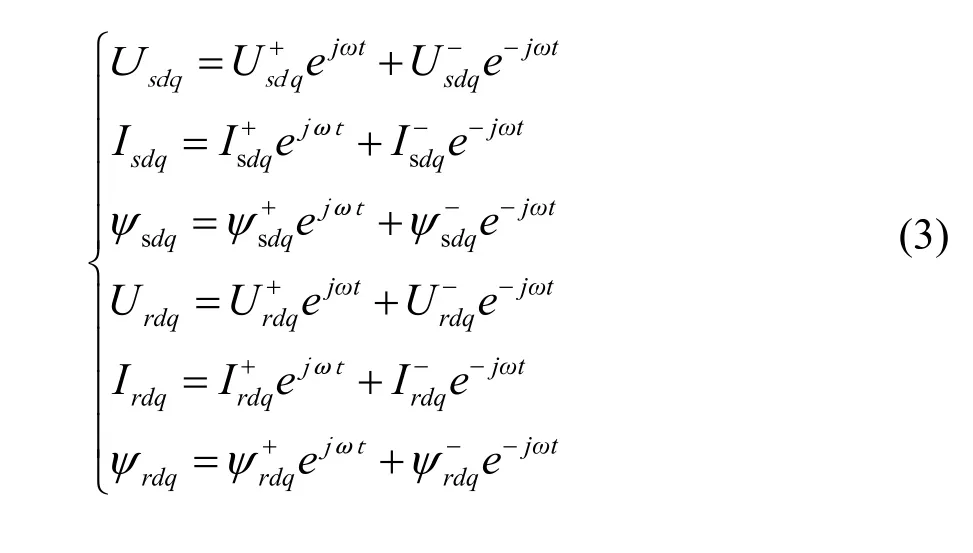
2 不平衡电网电压下的DFIG的瞬时功率

与平衡电网电压相类似，定子输出的有功、无功功率的表达式为：

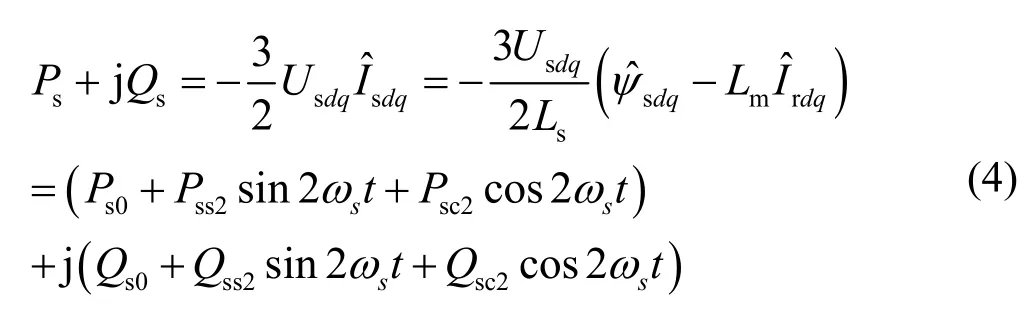
式中，p0，q0为有功，无功功率的平均值；pc2，ps2为二次有功余弦，正弦谐波峰值；qc2，qs2为二次无功余弦，正弦谐波峰值；ωs为电网频率。将式(3)代入后展开可得：

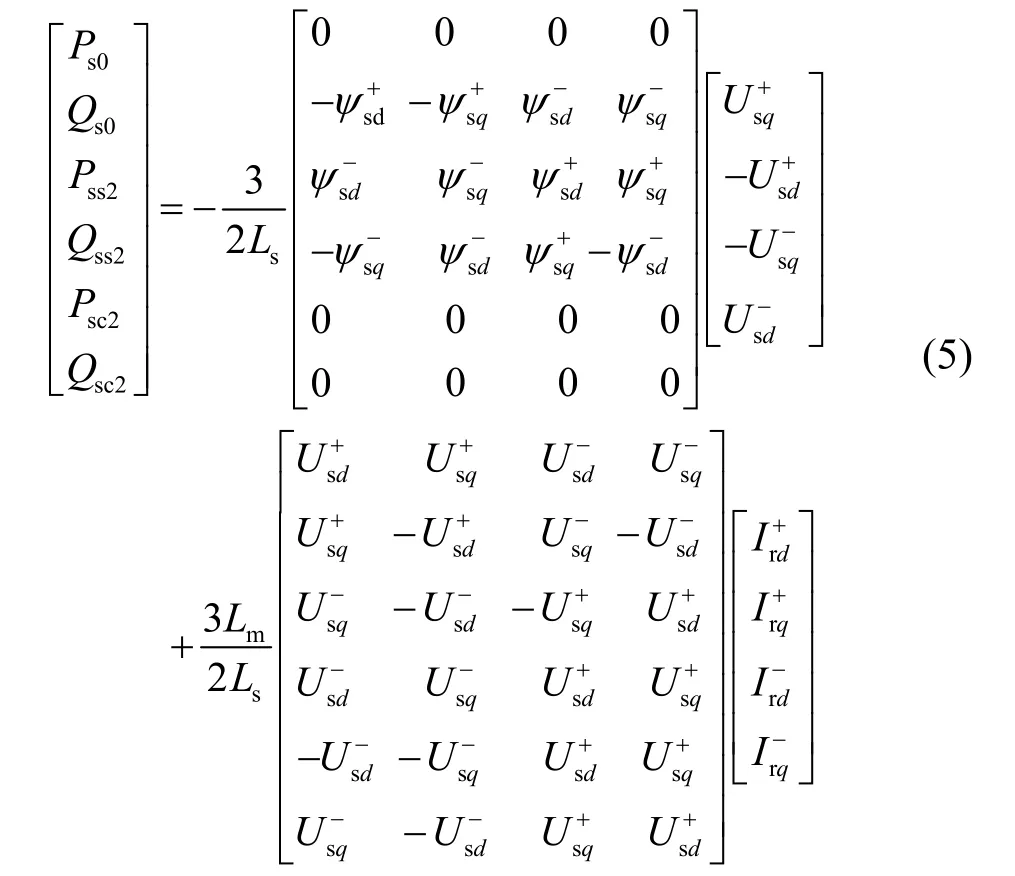
由式(2)可得，当忽略定子电阻时：

将式(3)代入式(6)可得：

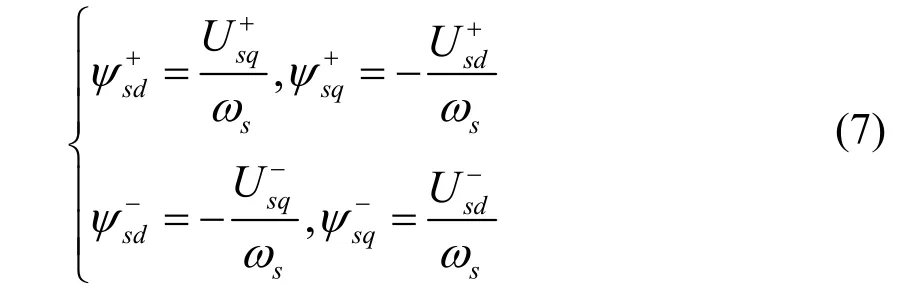
在本文中，采取 DFIG定子电压定向的矢量控制方式，及Usq+=0，可得ψsd+=0。

3 DFIG转子侧变流器的控制策略

电网电压发生不对称跌落时，电路中的电压和电流都存在着正负序分量。而由于负序分量会导致控制性能变差，因此要求转子侧变流器除确保 DFIG输出平均有功、无功功率以外，还应该确保整个发电系统中无负序电流的输出，本文采用一种抑制转子电流负序分量的控制方式。

为了抑制转子电流负序分量，在设计控制指令时，令转子电流负序分量的给定电流：Id-*=Iq-*=0，代入式(5)可得出转子电流正序分量的给定量：

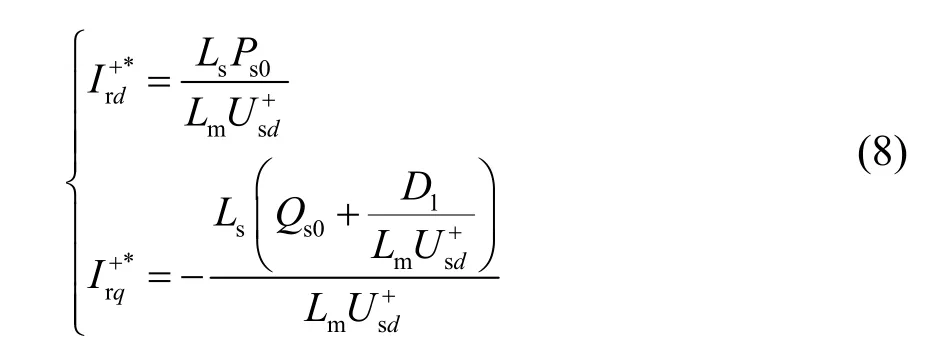
由式(2)可知转子侧变流器的电压方程为：

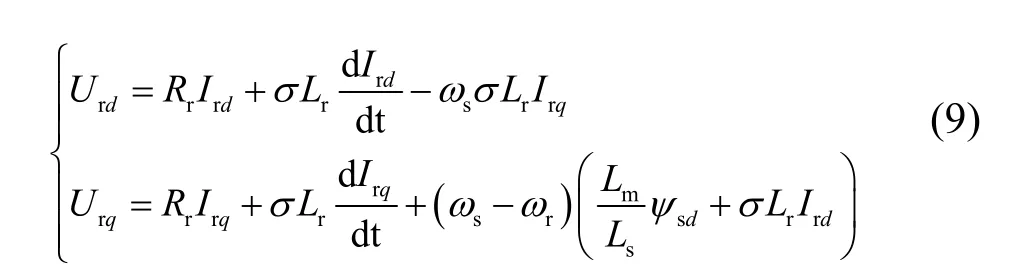
式(9)中σ=1-Lm2/LsLr为漏感因数，根据式(8)，(9)可得到在电网电压发生不对称跌落下转子侧变流器的控制策略，控制框图如图3所示。图中的Urdq+`,Urdq-`为电压补偿量。

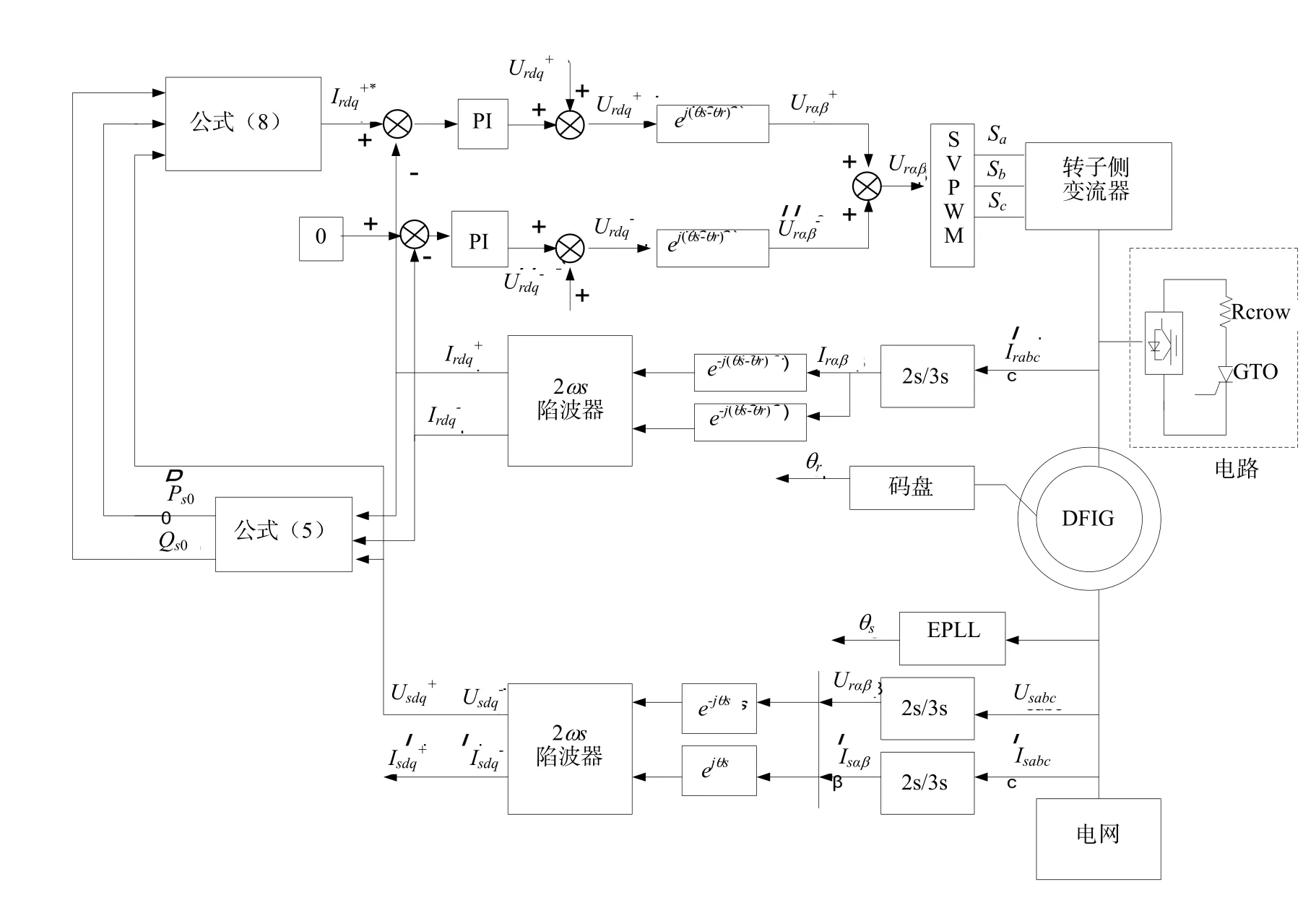
图3 转子侧变流器在电网电压不平衡跌落条件下的控制框图

由式(7)，(9)可计算得：

电网电压在发生不对称故障时，此时电网电压存在着负序分量，为了跟踪电网的频率和相位，于是在正向旋转坐标系dq+下，电网电压的q轴分量存在二倍频的波动分量，因此在锁相环的设计中，须加滤波设计，对二倍频的波动分量进行滤除，为此在设计增强型锁相环(EPLL)中采用了在q轴分量上加入了陷波频率为2倍频的陷波器，其结构框图如图4所示。

4 DFIG的Crowbar保护策略

当电网电压发生大值跌落时，此时 DFIG发出的功率不能及时送出，可能导致转子侧变流器的过流和直流母线的过电压，为了保护变流器免受过流和过压的危害，流过转子侧变流器的电流须限制在其限额以内，可采用将转子侧变流器与转子回路断开，将转子保护电路接入转子回路的方案，此保护电路称为Crowbar电路。当电压发生小值跌落时，这种状态下可通过图3所示控制系统的适当设计使其转子侧的电流保持在其限额内，无需保护动作。当电网电压发生较大的跌落时，此时转子侧变流器的过流将不可避免，这种情况下将启动 Crowbar电路渡过这段危险时间直到电压恢复正常时。

图4 增强型PLL结构框图

对于 Crowbar电路采用滞环比较器(如图 5所示)来对其进行控制，当转子电流|Ir|大于预先设置的阀值IH时，比较器输出1，此时Crowbar电路接入转子回路，转子侧变流器被短路。当转子电流|Ir|小于预先设置的阀值IL时，比较器输出0，这时Crowbar电路将不启动。设定IH=1.7p.u.，IL=1.4p.u.。

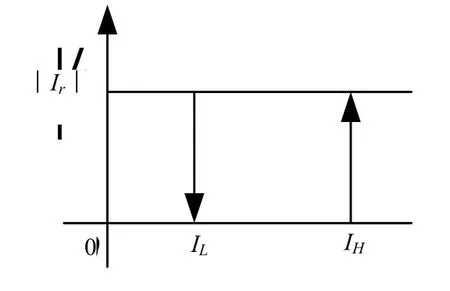
图5 滞环比较器

5 系统仿真研究

为了验证在不对称电压跌落条件下，转子侧变流器控制策略的有效性，采用图6所示的DFIG发电系统进行仿真，系统参数见表1。

图6 DFIG风力发电系统模型图

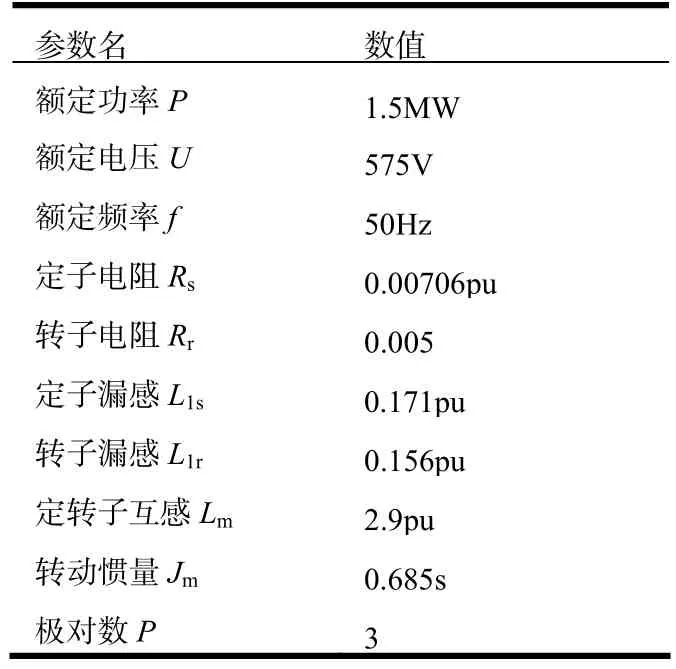
表1 DFIG仿真参数

5.1 小值不对称跌落时

设定A相电压在0.56s时发生单相短路故障，电压跌落25%，0.7s时故障解除。为比较分析，图7为传统控制策略的仿真波形，图8为采用图2所示的控制策略的仿真波形图。从图 7可看出，其电网功率，电磁转矩在0.56s以后波动较大存在大量的二次纹波。而图3所示的控制策略可以有效的减小负序分量的影响，从图 8可看出，其电网功率和电磁转矩的波动较小，证明了此控制策略的可行性。

5.2 大值非平衡跌落时

设定A相电压在0.56s跌落至0.15p.u.，0.7s时故障解除。其仿真结果如图9所示。其中ICrowbar为Crowbar电路的电流。可见当电网电压发生大值跌落后，转子电流急剧升高，达到阀值IH时触发Crowbar电路中的门极可关断晶闸管(GTO)导通，同时转子侧变流器与发电机转子解列，转子电流通过Crowbar消耗在RCrow上而减小。当转子电流减小到小于IL后，GTO关断转子侧变流器重新投入工作。由此可见采用Crowbar电路可以抑制电压发生大值跌落下的浪涌电流，保护转子侧变流器。

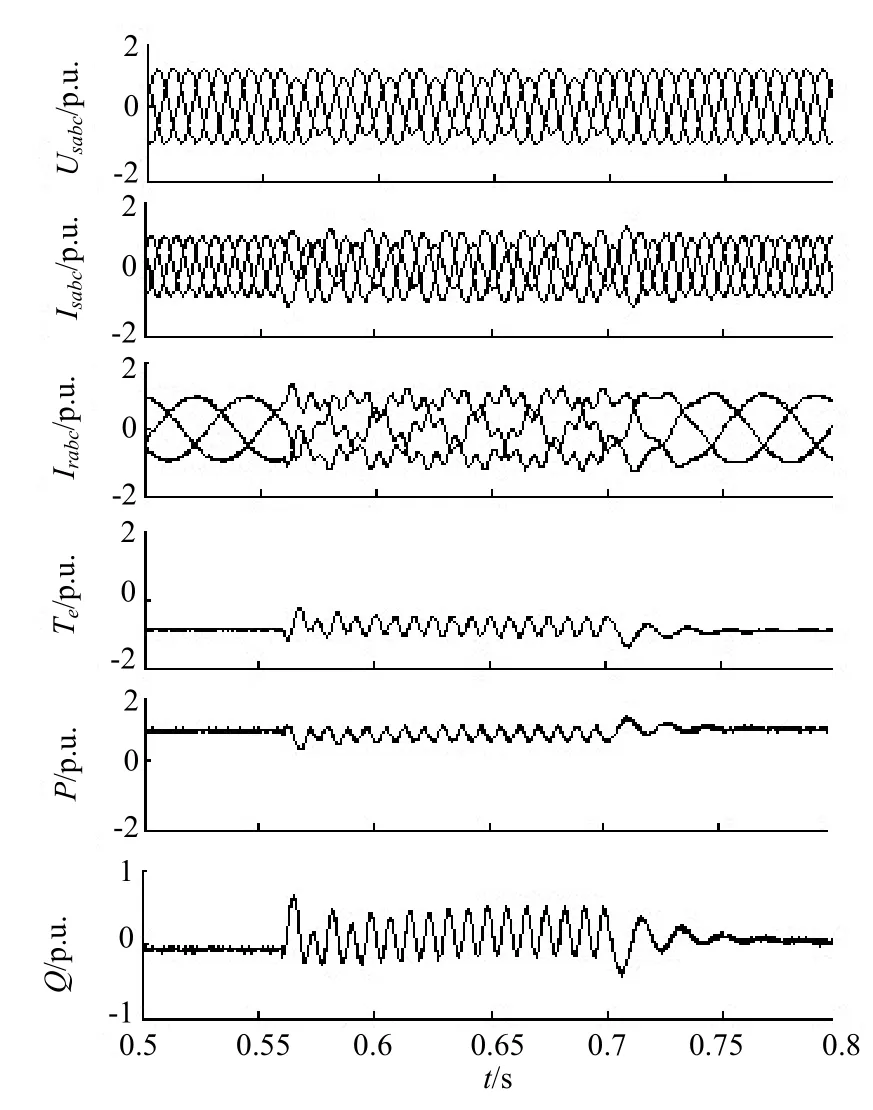
图7 采用传统控制策略的仿真结果

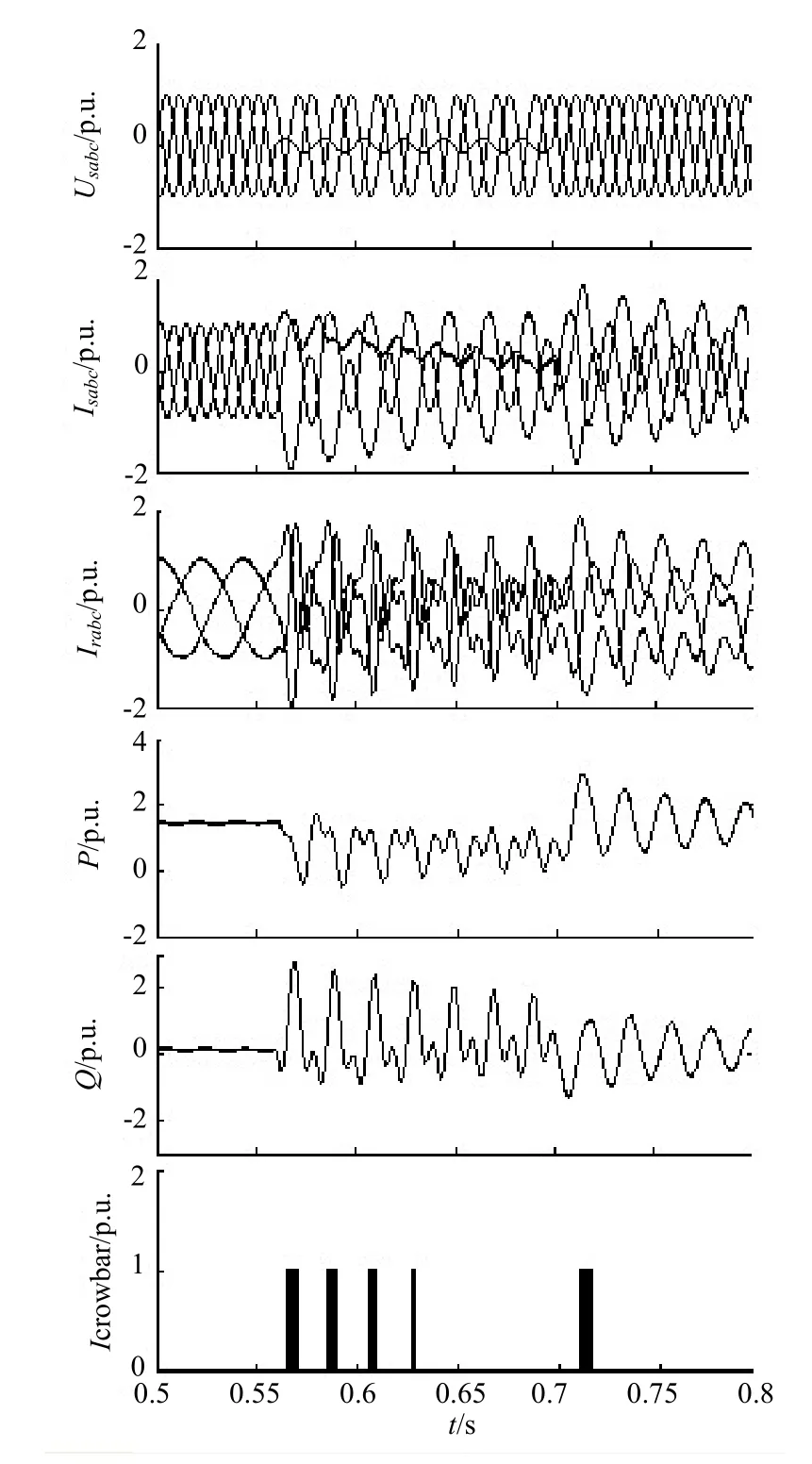
图9 电网发生大值跌落时的仿真结果

6 结论

本文针对电网电压不对称故障状态下传统控制策略的缺点，在增强型锁相环的基础上建立了 DFIG转子侧变流器的改进的控制策略，采用的是抑制转子电流负序分量的方案，此控制策略可有效的减小转子电流的谐波含量，电磁转矩的脉动和电网功率的二次纹波。并在一台额定功率为1.5MW的DFIG样机上进行了仿真，证明了此控制策略的可行性。

[1]周鹏, 贺益康, 胡家兵. 电网不平衡状态下风电机组运行控制中电压同步信号的检测[J]. 电工技术学报, 2008, 23(5)：108-113.

[2]胡家兵, 贺益康, 王宏胜, LIE Xu. 不平衡电网电压下双馈感应发电机网侧和转子侧变换器的协同控制[J]. 中国电机工程学报, 2010, 30(9): 97-104.

[3]王宏胜, 章玮, 胡家兵, 贺益康. 电网电压不对称故障条件下 DFIG风电机组控制策略[J]. 电力系统自动化, 2010, 34(4)：97-102.

[4]XU Lie, WANG Yi. Dynamic modeling and contol of DFIG-based wind turbines under unbalanced network conditions[J]. IEEE Trans on Power Systems, 2007, 22(1): 314-323.

[5]Peng Zhou, Yikang He, Dan Sun. Control and Protection of a DFIG-Based Wind Turbine under Unbalanced Grid Voltage Dips[J]. IEEE Transon Power Systems, 2009, 12 (26):1-8.

[6]蒋雪冬, 赵舫. 应对电网电压骤降的双馈感应风力发电机Crowbar控制策略[J]. 电网技术, 2008,32(12): 84-89.