基于Stribeck摩擦模型的无刷直流电机控制系统设计与仿真

许 宏， 张 怡， 王 凌， 陈锡爱

(中国计量学院，浙江杭州 310018)

0 引言

在机器人运动控制系统中，无刷直流电机(Brushlss DC Motor，BLDCM)因其体积小、重量轻、效率高、惯量小和控制精度高，同时还保留了普通直流电动机优良的机械特性等优点而被广泛应用。本文在分析BLDCM数学模型的基础上，建立控制系统转速电流双闭环的计算机仿真模型，由于系统在实际运行中存在摩擦负载的作用，常规PID控制虽原理简单、稳定性好、鲁棒性强，但其难以对摩擦负载中的强非线性系统进行有效控制，而模糊控制可以对复杂的非线性系统进行有效控制，具有较强的自适应能力。基于以上原因，本文提出了基于Stribeck摩擦模型的模糊PID控制，既能实现精确控制，又有较强的自适应能力，更有效地实现人的控制策略。

1 永磁BLDCM数学模型

本文以两相导通星形三相六状态为例，分析BLDCM的数学模型及电磁转矩等特性。为了便于分析，假定:

(1)三相绕组完全对称，气隙磁场为方波，定子电流、转子磁场分布皆对称;

(2)忽略齿槽、换相过程和电枢反应等的影响;

(3)电枢绕组在定子内表面均匀连续分布;

(4)磁路不饱和，不计涡流和磁滞损耗。

则根据BLDCM特性，可建立其电压、转矩状态方程以及等效的BLDCM电路。

1.1 电压方程

BLDCM三相定子电压的平衡方程可用以下状态方程表示:

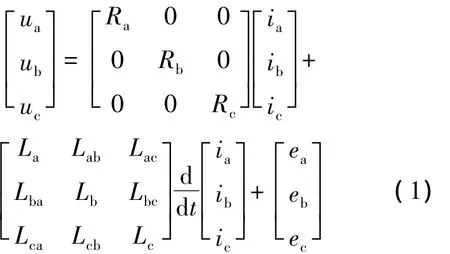
式中:ua，ub，uc——三相定子电压;

ea，eb，ec——三相定子的反电动势;

ia，ib，ic——三相定子相电流;

La，Lb，Lc——三相定子自感;

Lab，Lac，Lba，Lbc，Lca，Lcb——三相定子互感;

Ra，Rb，Rc——三相定子绕组的相电阻。

对于凸装式转子结构，忽略凸极效应，则定子三相绕组的自感和互感为常数，且与转子位置无关，因此 Ra=Rb=Rc，Lab=Lac=Lba=Lbc=Lca=Lcb=M，La=Lb=Lc=L。

若定子绕组三相Y形连接且三相绕组无中线引出，则有:ia+ib+ic=0，以及 M·ia+M·ib=-M·ic，则式(1)可表示为式(2)，由式(2)可得BLDCM的状态方程(式(3))和等效电路(见图1)如下。

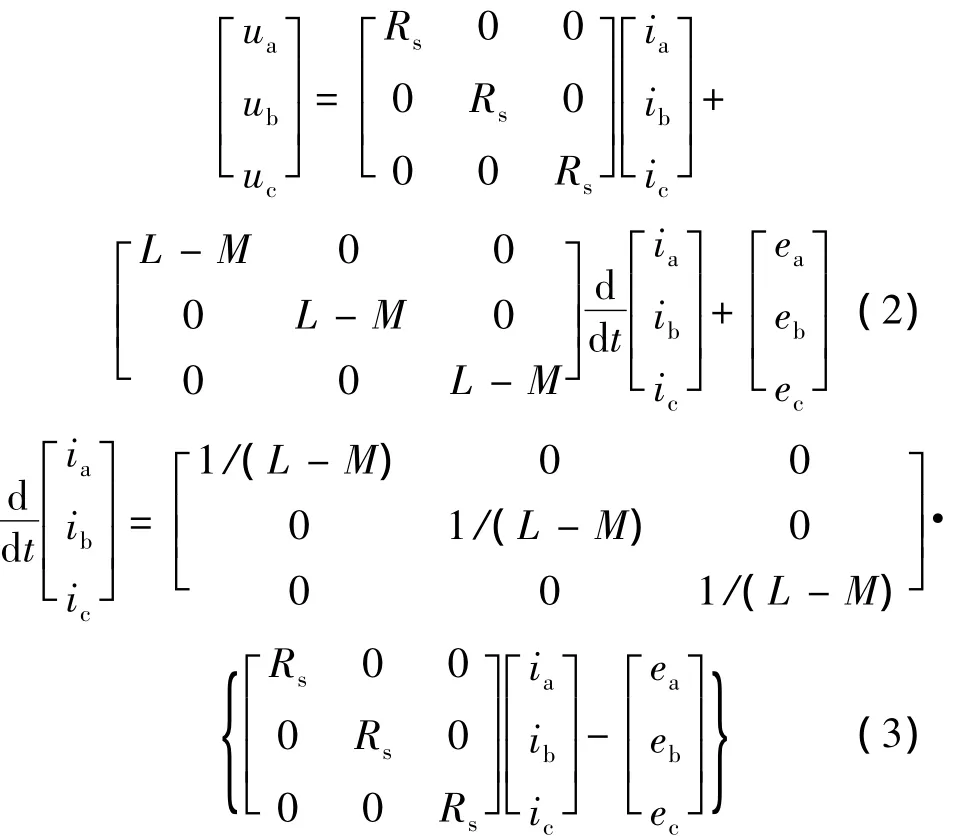
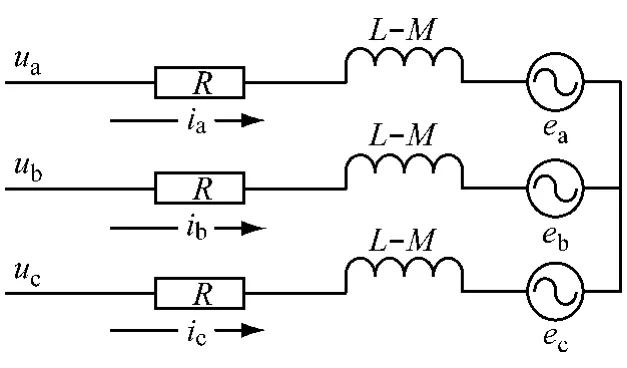
图1 永磁BLDCM等效电路模型

1.2 转矩方程

BLDCM的电磁转矩方程可表示为

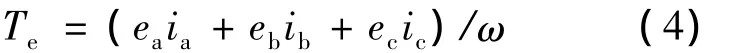
式中:ω——BLDCM的角速度。

BLDCM的运动方程可表示为

式中:B——阻尼系数;

J——电机的转动惯量;

TL——负载转矩。

1.3 动态数学模型

假设各相绕组对称，参数为常数，在A相和B 相导通时，ic=0，ia=-ib，设 I(t)=ib，由式(2)可得:

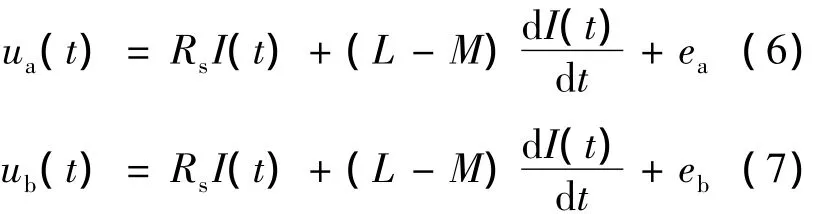
结合式(6)、(7)可得:

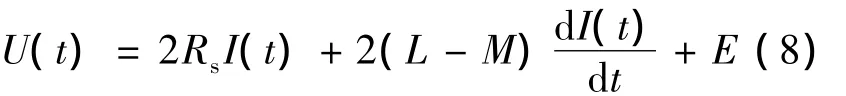
式中:U(t)——逆变器输出电压，U(t)=ua-ub;

E——平均反电动势，E=ea-eb。

根据反电动势与转速成正比，E可近似表示为E=ken，考虑到转矩与电流大小成正比，电磁转矩可表示成:Ta=kTL(t)，将两式带入式(8)并取其拉氏变换，可得BLDCM的动态特性为

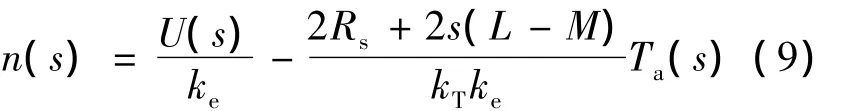
将运动学方程写成转速n的形式，并取拉氏变换得到:

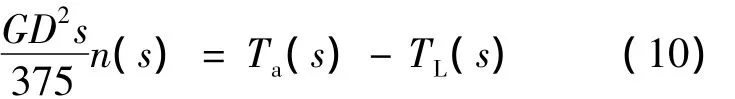
式中:GD2——转子的飞轮转矩;

TL(s)——电机的负载转矩。

其动态结构图如图2所示。

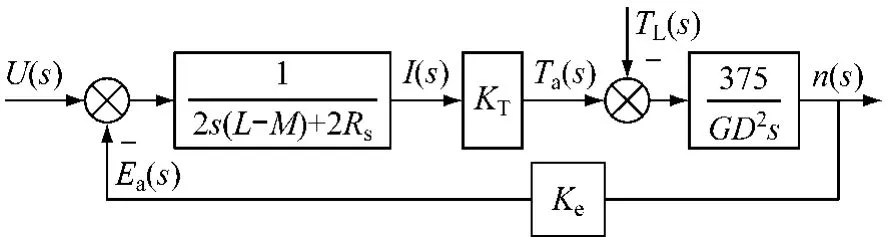
图2 永磁BLDCM动态结构图

2 摩擦负载模型

2.1 摩擦介绍

摩擦是一种复杂的、非线性的、具有不确定性的自然现象，而摩擦力是影响伺服控制系统性能的主要因素之一，会使系统出现爬行、振荡或稳态误差，降低运动系统的性能。一个有效的解决办法是引入对消项，以消除摩擦力，这称为摩擦补偿。

2.2 Stribeck摩擦模型

对摩擦非线性环节建立准确的数学模型，对摩擦现象和对其进行补偿都非常重要。目前，在工程中经常采用的有库仑摩擦模型、库仑摩擦+粘滞摩擦模型、静摩擦+库仑摩擦+粘滞摩擦模型和Stribeck摩擦模型。本文中的摩擦负载选用可以较为准确地反映摩擦力负阻尼特性的Stribeck摩擦模型(见图3)，其采用速度的指数函数来描述摩擦的非线性。Stribeck摩擦模型可表示为当|˙θ(t)|＜α时，静摩擦为

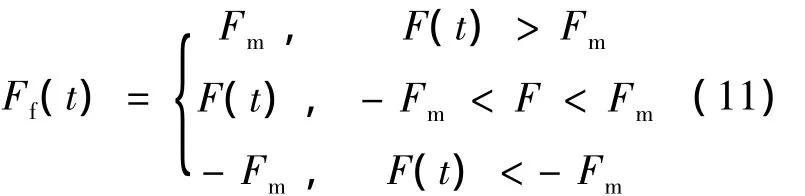
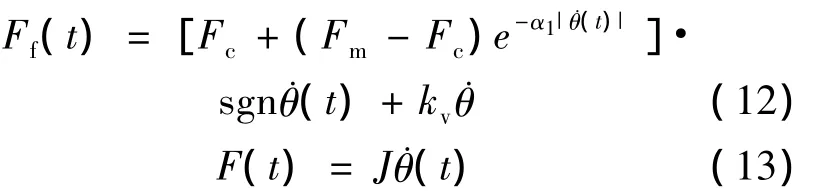
式中:F(t)——驱动力;

Fm——最大静摩擦力;

Fc——库仑摩擦力;

kv——粘性摩擦力矩比例系数;

α、α1——非常小的正常数。

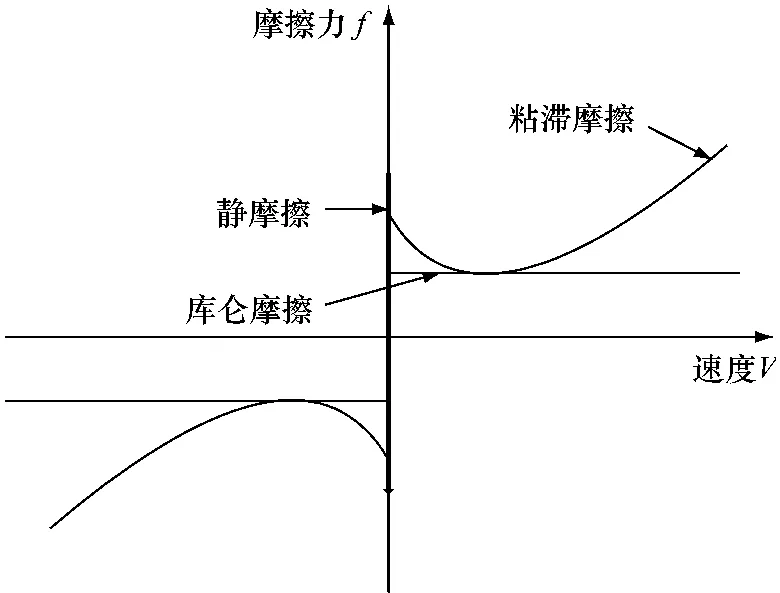
图3 Stribeck摩擦模型示意图

3 BLDCM控制系统设计与仿真

3.1 BLDCM双闭环控制系统

基于Stribeck摩擦模型的BLDCM控制系统如图4所示。该控制系统由电流和转速两个控制环节构成，其中电流环作为内环，而转速环则作为外环。

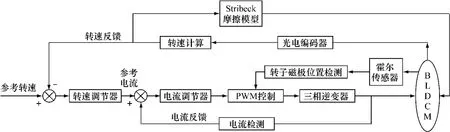
图4 基于Stribeck摩擦模型的BLDCM转速控制系统的控制框图

3.2 转速、电流调节器设计

在传统的电机控制系统中，转速、电流调节器大多采用PID控制:PID控制是最简单实用的一种控制方法，其控制参数既可以依靠数学模型通过解析的方法进行整定，也可以不依赖模型而凭经验和试凑来整定。但本文的BLDCM控制系统由于考虑了摩擦因素的影响，系统具有很强的非线性，而传统PID控制本质上是一种线性控制器，鲁棒性较差，无法达到满意的控制效果，在速度跟踪时有明显的“死区”现象。

20世纪90年代发展起来的采用人工智能技术，综合专家或现场操控人员的知识和经验构成知识库，模仿人的思维决策过程，实现自动调整PID控制参数的模糊自适应PID，可以将精确的问题模糊化，并运用模糊推理和解模糊化处理，实现对PID参数的最佳调整。模糊自适应PID的结构原理如图5所示。

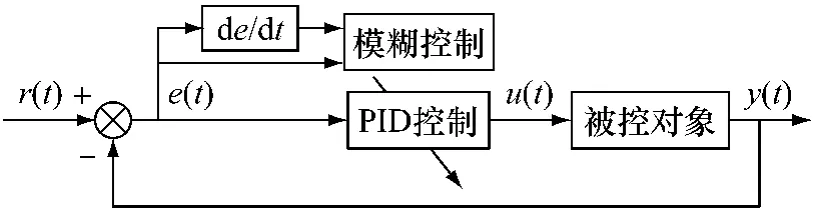
图5 模糊自适应PID结构原理图

本文的转速、电流调节器均采用模糊自适应PID控制，其控制器输入量分别为转速差、转速差变化率和电流差、电流差变化率;输出为各控制器的PID参数。以上各变量的论域均划分为{NB，NM，NS，ZO，PS，PM，PB}七个模糊子集，隶属度函数采用三角形分布，如图6所示。

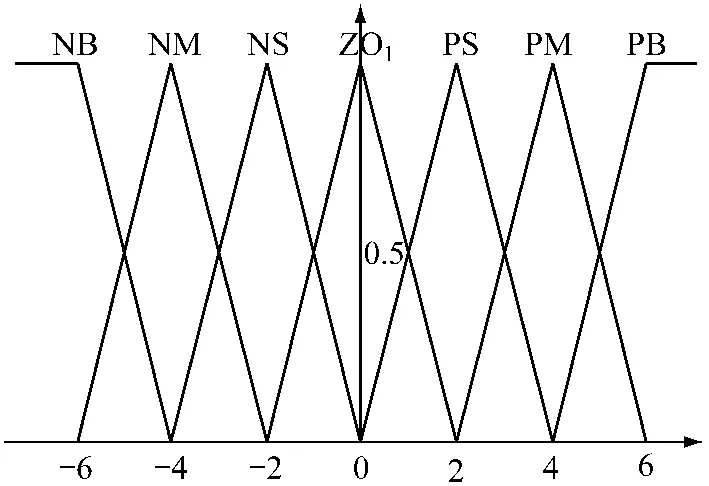
图6 隶属度函数分布图

根据实际经验制定模糊规则，模糊控制规则制定原则为:曲线振荡很频繁，增大kp值，曲线漂浮绕大弯，减小kp值;曲线偏离回复慢，增大ki值，曲线波动周期长，减小ki值;曲线振荡频率快，减小kd值，动差大而波动慢，增大kd值。

3.3 基于Stribeck摩擦模型的BLDCM控制系统仿真

基于Stribeck摩擦模型的控制系统Simulink仿真结构如图7所示。采用MATLAB的S-function模块实现Stribeck摩擦模型，图8为其Simulink框图，图9为模糊PID控制器仿真结构图。

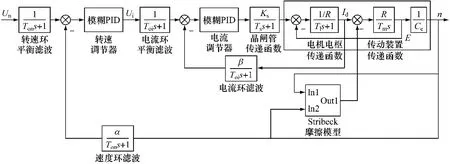
图7 基于Stribeck摩擦模型的双闭环调速系统的Simulink动态结构图

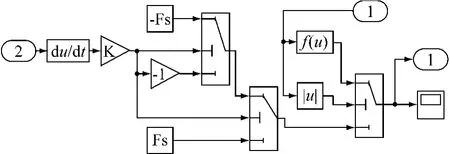
图8 Stribeck摩擦模型的Simulink框图

相关参数如下:R=0.518 Ω，TL=0.255 ms，Tm=7.3 ms，1/Ce=389 r/min，β =5.73 V/A，α =1/389 Vmpr，Toi=0.314 ms，Ton=6.28 ms，Ks=1，Ts=12.5 μs，Fc=15 N·m，Fm=20 N·m，Kv=2.0 Nms/rad，α1=1.0，α =0.01。

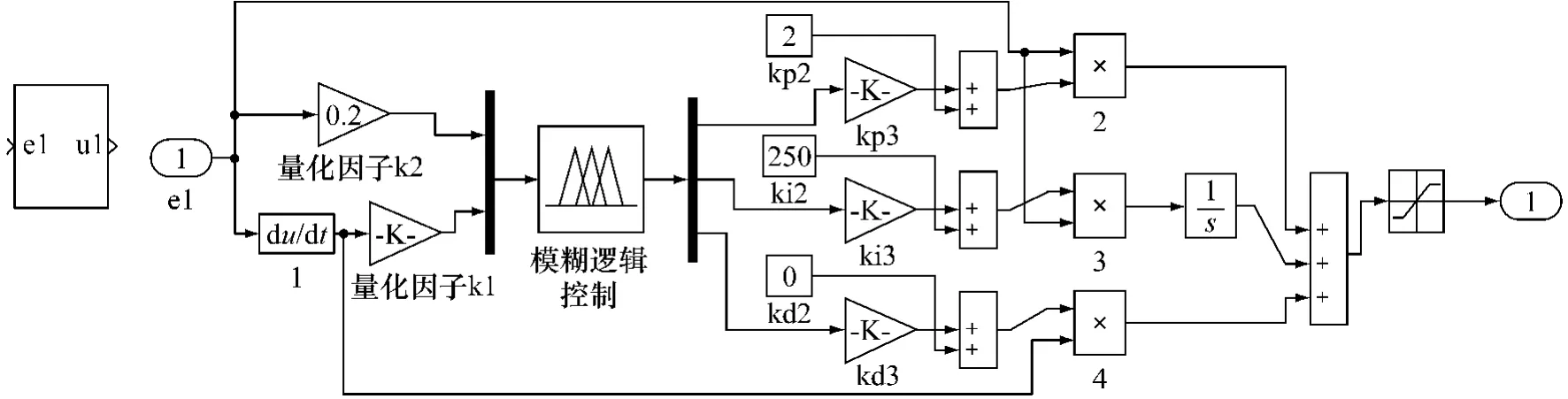
图9 模糊PID控制器仿真结构图

在终值为1 000的阶跃信号作用下，计入Stribeck摩擦模型，采用常规PID算法和模糊PID算法时得到的系统速度响应曲线如图10所示。控制系统由于摩擦力的作用，在常规PID算法补偿下，系统响应超调量大，且稳态精度较差，而在模糊PID算法补偿下，系统响应无超调，稳态精度高。可见模糊PID算法在系统有摩擦负载的情况下可以有效提高系统的稳定性和控制精度。

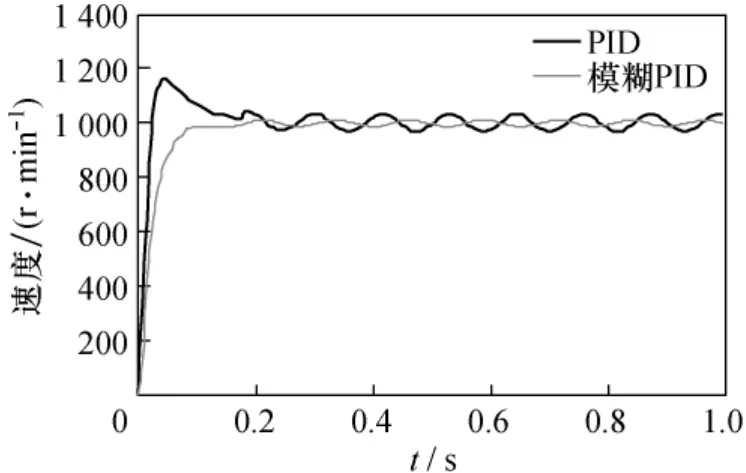
图10 阶跃信号下系统速度响应曲线

为检验系统的速度跟踪效果，在幅值为0.6的正弦信号激励下，系统速度跟踪响应如图11所示。对比图11(a)、(b)可见，采用常规PID算法控制时，系统存在速度跟踪“死区”现象，使系统响应曲线发生畸变;采用模糊PID算法控制时虽有抖动，但其过死区时间短、精度高，其输出曲线更加逼近给定输入信号曲线。因此，采用模糊PID算法可以有效提高系统的速度跟踪精度。

图12为系统在给定输入下的Stribeck摩擦模型的摩擦力矩变化曲线。

4 结 语

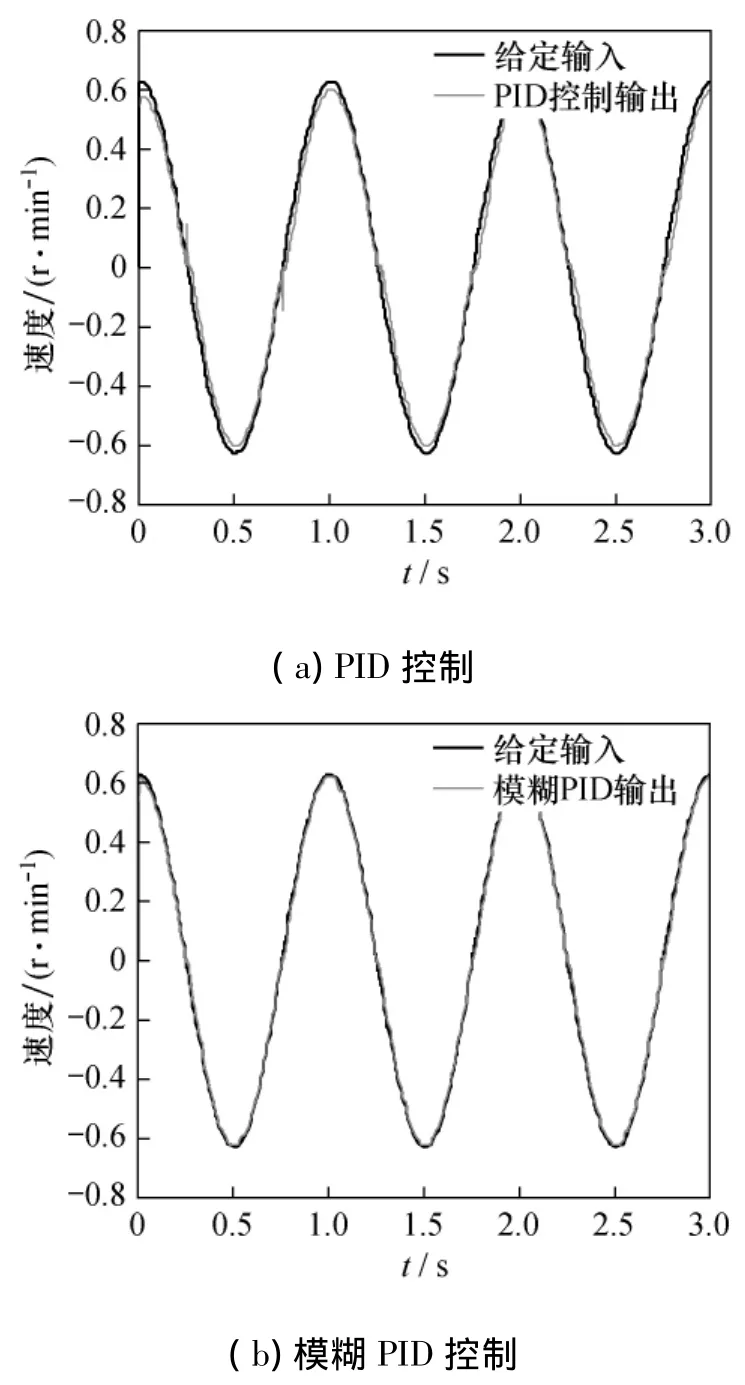
图11 正弦信号激励下的速度响应曲线

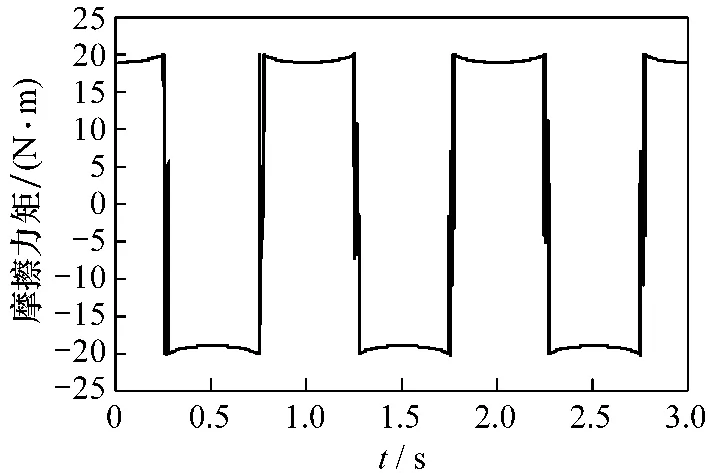
图12 摩擦力矩变化曲线

本文在BLDCM控制系统的设计中，考虑到系统在实际运行中存在摩擦负载的作用，采用常规PID控制时系统稳态精度和鲁棒性较差，速度跟踪存在明显的“死区”现象，提出了一种基于Stribeck摩擦模型的模糊PID控制算法。经过对仿真曲线的分析比较，得知采用模糊PID控制算法时，阶跃响应无超调、响应快、稳态精度高;速度跟踪虽有抖动，但其过死区时间短、精度高，其输出曲线更加逼近给定输入信号曲线。

［1］龙驹.永磁无刷直流电动机转速控制系统的优化设计［M］.成都:西南交通大学出版社，2006.

［2］Karnopp D Comput.Computer simulation of stick-slip friction in mechanical dynamic systems［J］.Journal of Dynamic Systems，Measurement and Control，1985(107):100-103.

［3］席爱民.模糊控制技术［M］.西安:西安电子科技大学出版社，2008.

［4］刘金琨.先进PID控制及其MATLAB仿真［M］.北京:电子工业出版社，2004.

［5］王丹力，赵剡.MATLAB控制系统设计仿真应用［M］.北京:中国电力出版社，2007.