永磁直线同步电机神经滑模控制仿真*

王 武， 白政民， 姚 宁

(许昌学院电气信息工程学院，河南许昌 461000)

0 引言

永磁直线同步电机(Permanent Magnet Linear Synchronous Motor，PMLSM)伺服系统去掉了电动机到工作台之间的机械传动环节，实现了“零传动”方式，故而构造的伺服系统具有响应速度快、精度高、传动刚度高、行程长、推力大及高效节能等一系列优点，并被广泛应用于工业机器人、数控机床等高精密加工领域。但是负载扰动、系统的非线性及耦合性、推力纹波等都会降低系统的伺服性能，需要采取好的技术措施和控制手段进行补偿和控制。滑模变结构控制其滑动模态对加给系统的扰动和系统参数摄动具有完全的自适应性，响应速度快，能够克服伺服系统所具有的非线性和不确定性，在伺服系统中得以广泛应用［1］。很多专家学者在不同角度提出了PMLSM的控制方法，文献［2］针对PMLSM伺服系统精度受非线性摩擦力和动子质量变化影响问题，设计了基于库仑摩擦的自适应摩擦补偿控制，通过对摩擦力的在线补偿，提高了位置跟踪精度;文献［3］通过初级反电动势计算定子电流谐波进行电流补偿减小推力波动，通过电动机结构优化设计和控制策略减小推力纹波;文献［4］应用模糊滑模控制型迭代学习伺服控制器实现数控机床直线进行伺服系统的鲁棒控制;文献［5］实现了PMLSM的自适应反推滑模鲁棒跟踪控制;文献［6］设计了基于神经网络推力观测器的新型滑模控制，削弱了推力波动及系统抖振问题;文献［7］构建了神经网络自适应滑模控制，提高对参数时变和外部扰动的鲁棒性。这些方法都取得了较好的控制效果。论文分析了PMLSM的数学模型，给出了径向基(Radical Basis Function，RBF)神经网络及学习算法，提出将滑模控制器的切换函数作为神经网络的输入、将滑模控制器作为神经网络的输出，实现神经滑模控制，充分发挥了滑模变结构控制通过控制器结构的不断调整和变化有效控制具有参数变化和外部扰动的被控对象，能够保证控制系统具有较强的鲁棒性，同时充分应用了神经网络在线自适应学习功能和泛化能力，通过MATLAB仿真环境分析了系统的控制性能。

1 PMLSM的数学模型

PMLSM是一个非线性强耦合多变量的动态系统，在建模时作如下假设:磁路为线性，忽略端部效应、齿槽效应及饱和效应;气隙磁场在空间按正弦分布，忽略磁场的高次谐波;忽略环境温度和电机温升对电机参数的影响。定义各参数如下［8］:ud，uq分别为 d、q 轴的定子电压;id，iq分别为 d、q轴的定子电流;Ld，Lq分别为 d、q轴的定子电压;Rs为定子电阻;Ψf为永磁铁产生的主磁链;FL为负载阻力;Bv为粘滞摩擦系数;p为极对数;τ为极距;v为动子运动速度。

PMLSM在d-q轴系下的数学模型可描述为

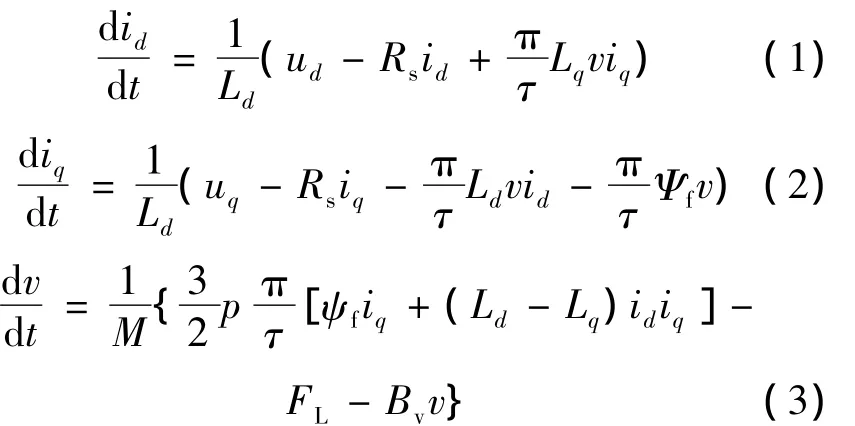
在采取id=0的控制策略后，PMLSM的数学模型可描述为

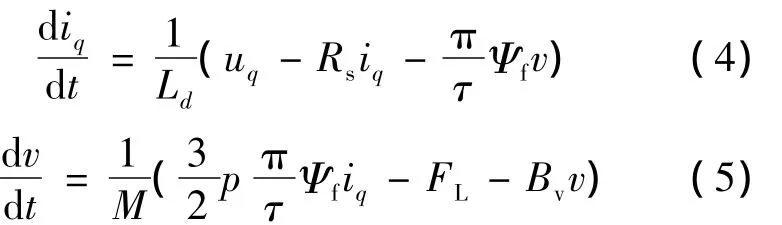
选取系统的状态变量:x=［iqv］T，控制量为u=［uq］，系统的状态空间表达式为

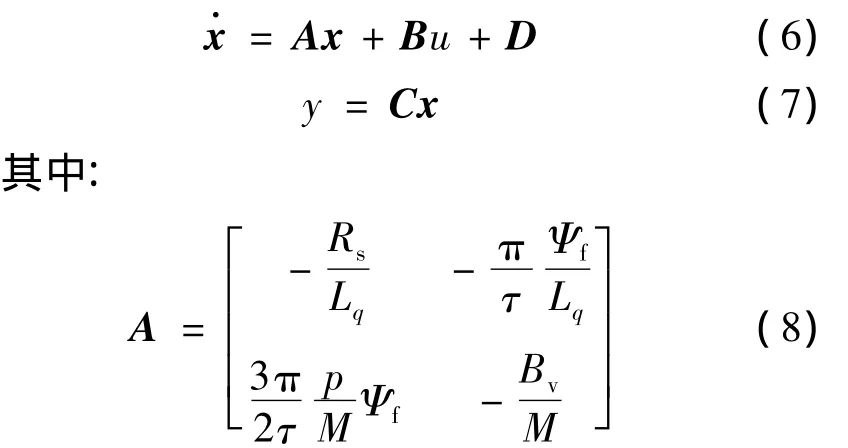
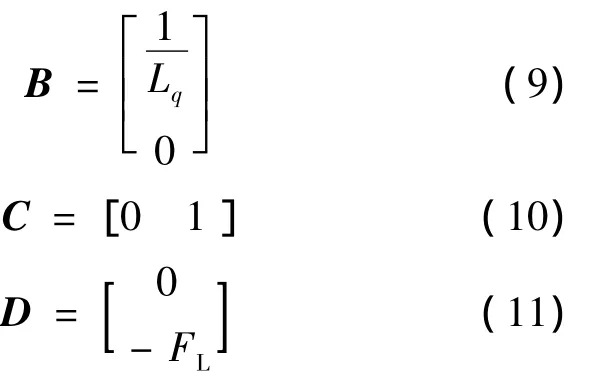
2 神经滑模控制

2.1 RBF神经网络及算法

RBF神经网络是具有单隐层的前向网络，输入控件到隐含层空间进行非线性变换，隐含层空间到输出层采用线性变换，可以大大加快学习速度并避免局部极小问题［9］。典型的RBF网络结构如图1所示。

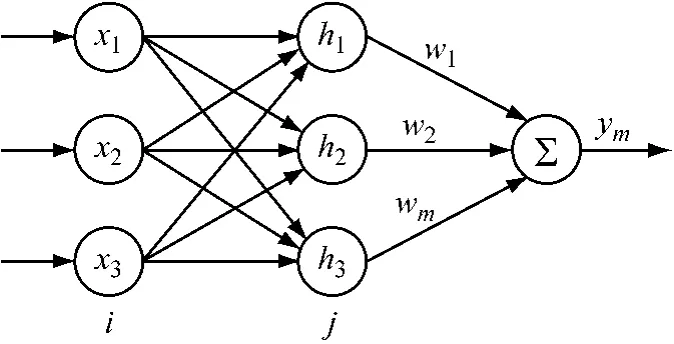
图1 RBF神经网络结构

在 RBF网络中，X=［x1x2…xn］T为网络的输入向量，H=［h1h2…hm］T为网络的RBF向量，其中hj为高斯基函数:

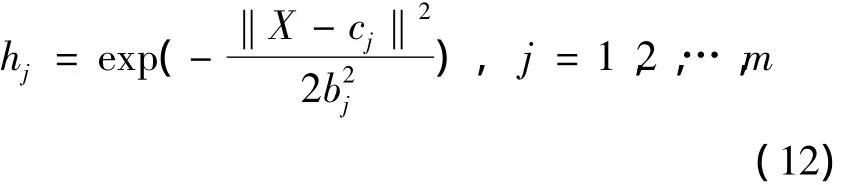
其中，cj=［cj1cj2…cjn］为网络第j个节点的中心向量。

网络的基宽向量为

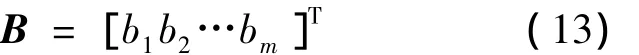
bj为节点j的基宽参数，网络的权向量为

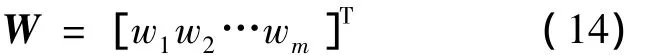
网络输出为

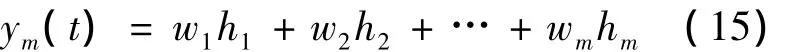
网络的性能指标函数为

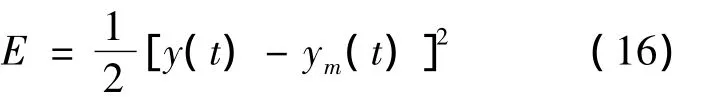
根据梯度下降法，迭代算法为［9］

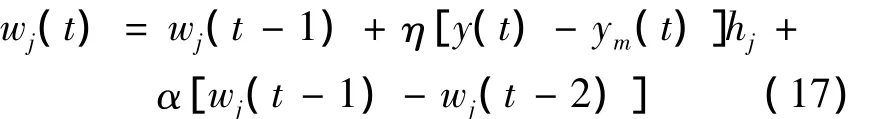
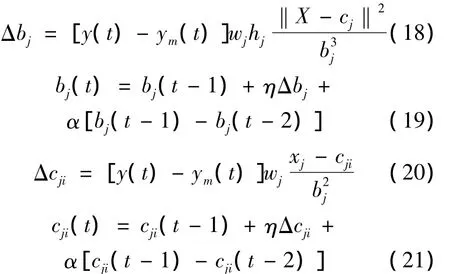
式中:η——学习率;

α——动量因子。

2.2 RBF神经滑模控制

神经滑模控制器结构如图2所示，将滑模控制器的切换函数作为神经网络的输入，将滑模控制器作为神经网络的输出，实现神经滑模控制。

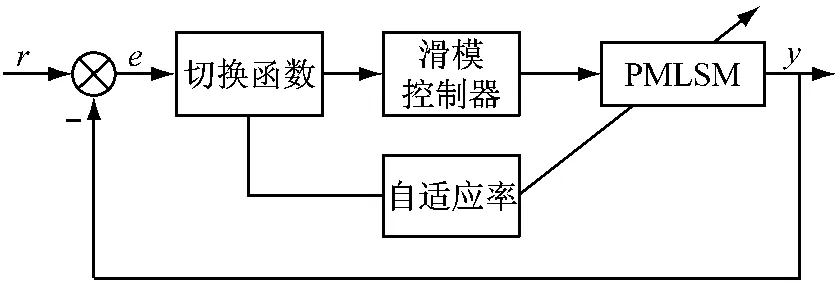
图2 神经滑模控制器结构

设被控对象为

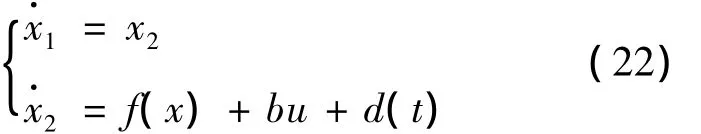
设位置指令为r(t)，切换函数设计为

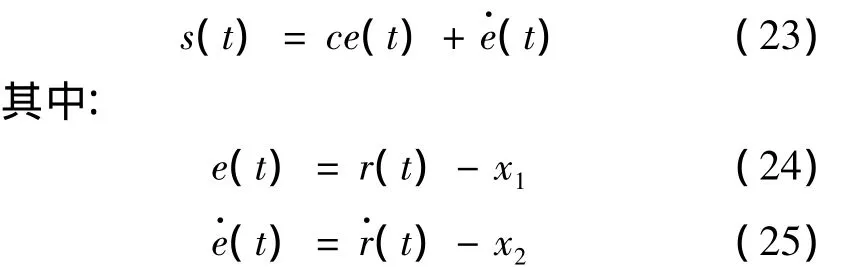
将滑模控制器设计为RBF网络的输出，即:

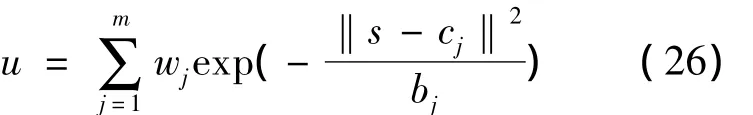
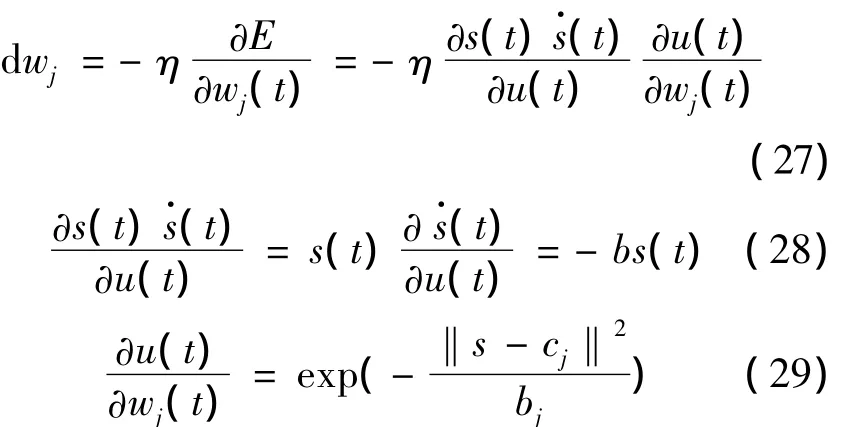
网络的权值学习算法为

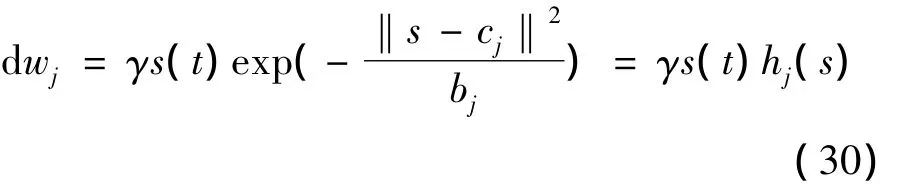
3 PMLSM神经滑模控制仿真

根据系统所构建的PMLSM的数学模型，采用文献中电机的相关参数，可得到对应电机模型中［11-13］:

在MATLAB环境下进行系统仿真，求得系统的传递函数模型为

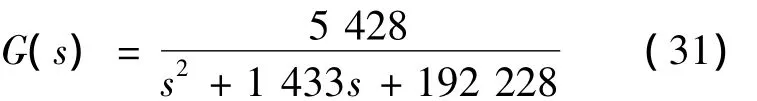
在不同的PID参数下，分析系统对阶跃信号、方波信号和正弦信号的跟踪能力，跟踪曲线如图3～5所示。为了实现信号的良好跟踪，要不断对PID参数进行人为调整，进而导出系统的能控标准型，利用神经滑模控制进行正弦信号跟踪。RBF神经网络参数选取如下，隐含层数目为5，高斯基函数中心向量取:c=［－4 －2 0 2 4］，基宽参数取:b=［1 1 1 1 1］;滑模控制器参数选取c=15，控制率中选取γ=2，动量因子α=0.02;系统输入位置信号为正弦 r(t)=sin(4πt)，对系统施加干扰信号为 d(t)=0.2sin(2πt)。图6为神经滑模控制下系统的位置跟踪曲线，图7为控制量输入曲线。

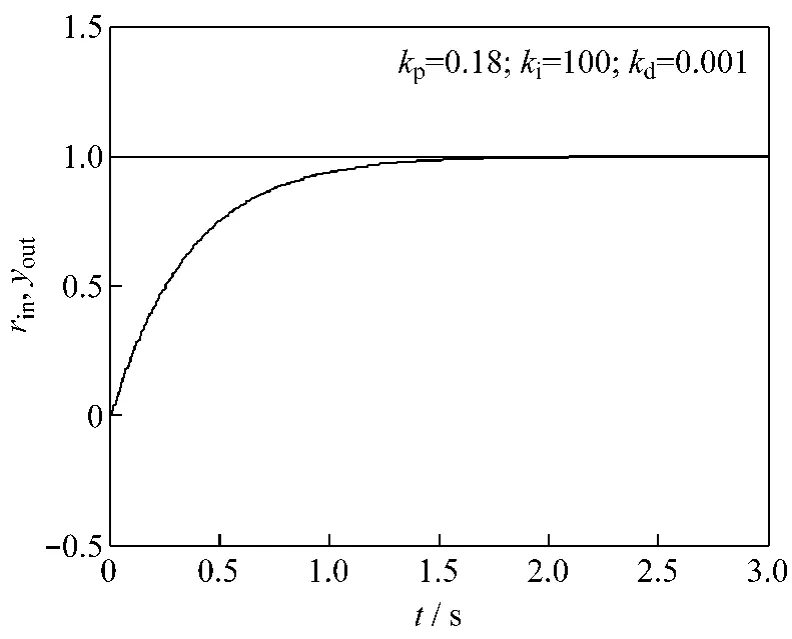
图3 PID控制下阶跃信号跟踪

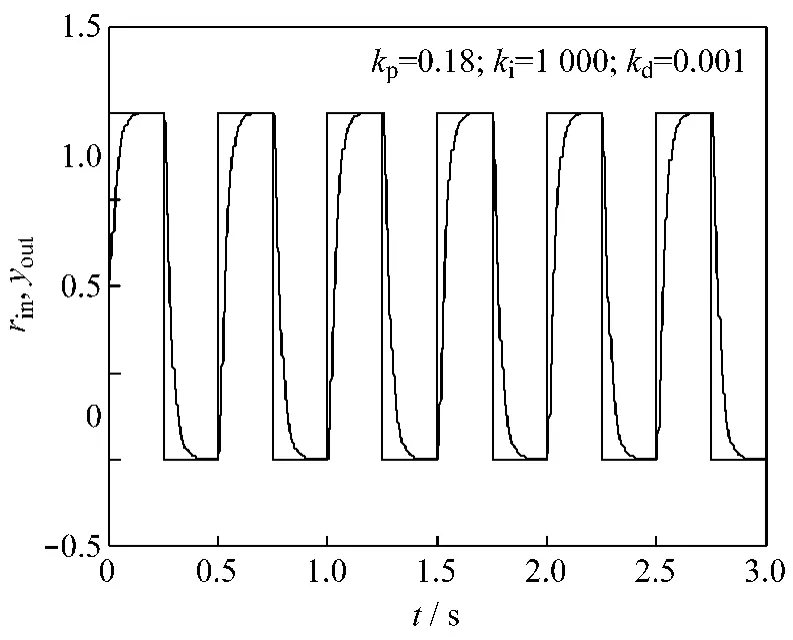
图4 PID控制下方波信号跟踪

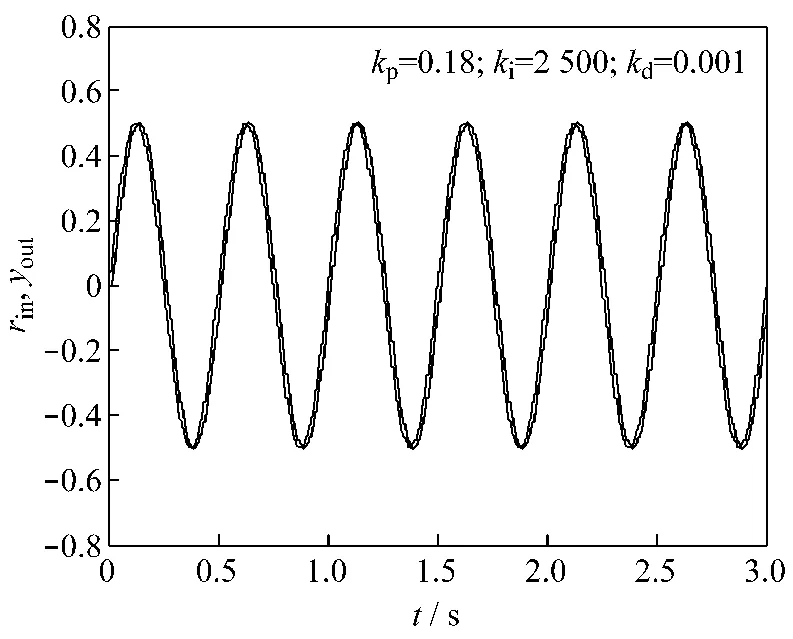
图5 PID控制下正弦信号跟踪

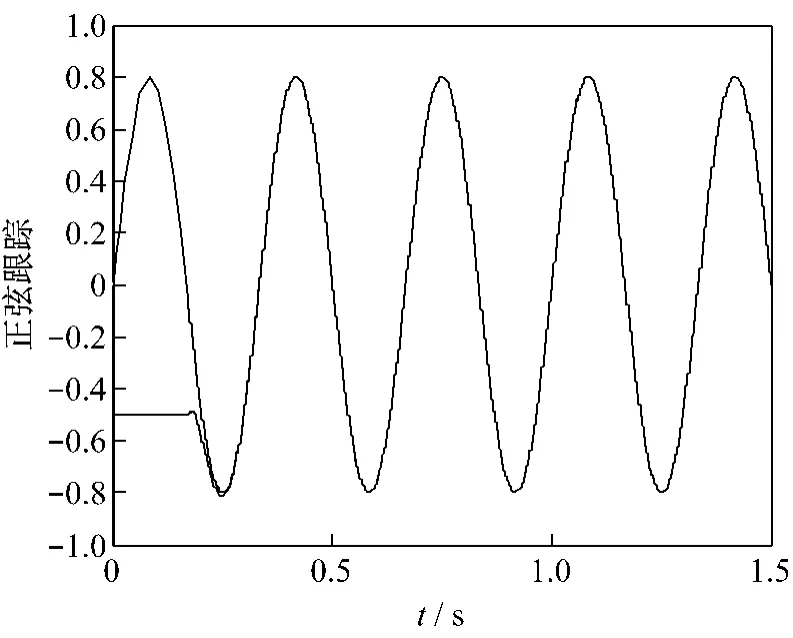
图6 神经滑模控制下正弦信号跟踪

4 结 语

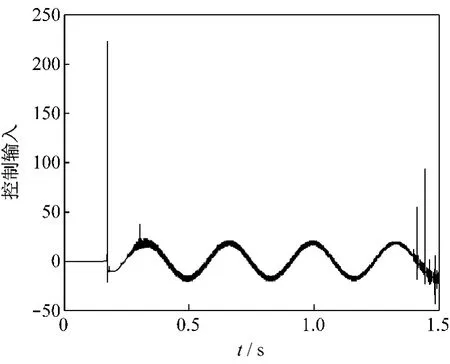
图7 神经滑模控制下控制信号

以PMLSM伺服系统为研究背景，结合RBF神经网络和算法，提出以切换函数为网络输入，以滑模控制器为网络输出，设计出稳定的自适应神经滑模控制器，在MATLAB仿真环境下进行了系统性能分析。通过对比可知，常规PID控制对静态模型具有一定的控制性能，当进行不同的信号跟踪时，要进行人为的参数调整，且跟踪精度不够高。本文设计的神经滑模控制器可实现较好的位置跟踪，并且神经网络可以有效地进行在线学习，参数可以自适应调整，实现了伺服系统的跟踪精度和低速平稳性，为PMLSM构建高性能伺服控制系统提出了一种有效方法，以期将仿真结论应用于实际工程，取得更好的实用价值和经济效益。

［1］王丽梅，武志涛，左涛.永磁直线电机自构式模糊神经网络控制器设计［J］.电机与控制学报，2009(9):643-659.

［2］王丽梅，武琳，刘春芳.永磁直线同步电动机自适应摩擦补偿控制［J］.沈阳工业大学学报，2009(6):252-276.

［3］付子义，李华群，刘爱军.抑制永磁直线同步电动机推力波动的补偿技术［J］.工矿自动化，2009(9):45-48.

［4］曹勇，李华德.机床直线进给伺服的FSMC型迭代学习控制研究［J］.中国机械工程，2009(7):1700-1703.

［5］陈刚，柴毅，丁宝苍，等.电液位置伺服系统的多滑模神经网络控制［J］.控制与决策，2009(2):221-225.

［6］李华群，付子义，薛增朝.基于新控制率的永磁直线同步电动机滑模控制［J］.电力电子技术，2009(7):23-25.

［7］杨伟民，潘丽姣，陆华才.基于神经网络的永磁直线同步电机自适应滑模控制［J］.电气自动化，2009(3):9-11.

［8］周振雄，杨建东，曲永印.基于DRNN的直线永磁同步电机精密位置控制［J］.机床与液压，2008(8):248-250.

［9］Parma G，Menezes B R，Braga A P，et al.Sliding mode neural network control of an inducton motor drive［J］.International Jouranal of Adaptive Control and Signal Processing，2003，17(6):501-508.

［10］高为炳.变结构控制的理论及设计方法［M］.北京:科学出版社，1996.

［11］侯伯杰，李小清，周云飞，等.直线电机伺服系统的复合前馈PID控制［J］.机床与液压，2009(2):56-58.

［12］潘霞远，刘希喆，吴捷，等.永磁同步直线电机的鲁棒PID控制［J］.电机与控制应用，2008(9):34-38.

［13］刘金琨.滑模变结构控制MATLAB仿真［M］.北京:清华大学出版社，2005.