无刷双馈风力发电机的H∞控制
2011-06-02蔡超豪
蔡超豪
(沈阳工程学院,辽宁沈阳 110136)
0 引言
能源、环境是当今人类生存和发展所要解决的紧迫问题。风力发电是一种无污染的绿色电力,由于无刷双馈风力发电机的特殊结构,降低了维护费用,提高了运行的可靠性,已成为风力发电研究的主要方向。
无刷双馈风力发电机运行于不同风速时有着不同的控制目标:当其运行于额定风速以上时,要求保持输出功率平稳;运行于额定风速附近时,要求保持转速稳定,实现恒转速运行;运行于额定风速以下时,要求实现最大风能捕获。由于气动性能的影响,无刷双馈风力发电机具有较强的非线性,此外,其转动惯量大、工作风速范围宽、发电机温度和转轴机械阻尼不断变化,数学模型复杂,因而实现精确控制较为困难。目前国内已发表的文献中有自抗扰功率解耦控制[1]、有功和无功功率控制[2]、最大风能追踪控制[3]、滑模变结构控制[4]、模糊控制[5]等,都取得了一定效果,但引入先进控制理论的文章还不多。H∞控制理论在系统建模和控制器设计过程中考虑了不确定性对系统的影响,利用解析方法设计控制器,能够使所有被控对象均能满足期望的性能指标,因此本文着力分析无刷双馈风力发电机全风速范围的H∞控制。
本文介绍了以下三部分内容:(1)利用基于等效旋转控制绕组的矢量控制模型,应用直接反馈线性化构建鲁棒控制模型,将线性化后估计出的非线性项的上界作为不确定项处理;(2)按H∞鲁棒控制理论,采用MATLAB工具箱进行求解,得出具备参数摄动鲁棒镇定性能和干扰抑制性能的最优控制器;(3)用实例和仿真验证该控制算法的有效性。
1 无刷双馈风力发电机简介
无刷双馈风力发电机的基本结构如图1所示,定子侧安装两套三相绕组:一套为功率绕组,磁极对数为pp,直接接工频电网;另一套为控制绕组,磁极对数为pc,通过变频器接电网。采用自行闭合的笼形转子或磁阻转子,无电刷和滑环。
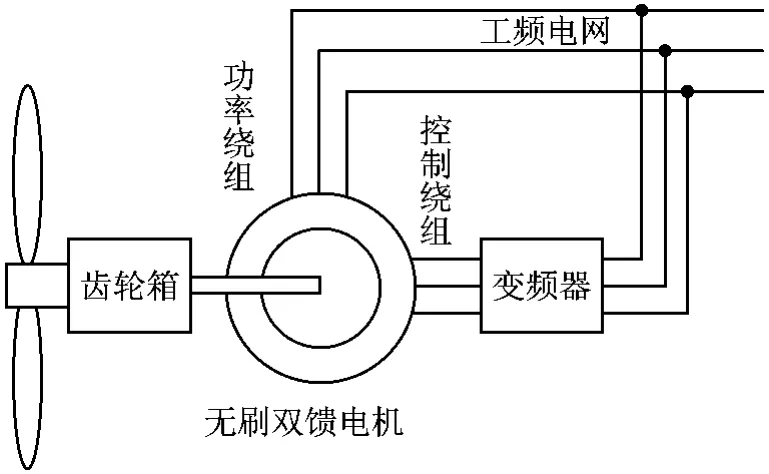
图1 无刷双馈风力发电机简图
无刷双馈风力发电机的频率与转速之间存在以下关系:
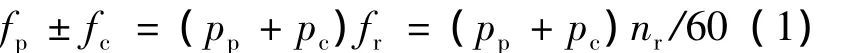
式中:fp、fc分别为功率绕组、控制绕组的电流频率,当绕组的相序相反时取正号,反之取负号;fr为发电机转子机械频率(fr=nr/60),转子磁极对数为np=pp+pc,在不同风速下发电机机械转速nr变化时,只要适当调节控制绕组输入电流的频率,即可使功率绕组输出电流的频率维持不变。
通过变频器调节控制绕组的电流频率及幅值,便可控制功率绕组的电压及频率,进行异步起动;并网后,通过调节控制绕组输入电流的幅值和相位,即可控制功率绕组输出的有功功率和无功功率,达到稳频稳压。变频器容量只是电机容量的一部分,降低了成本。
2 无刷双馈风力发电机系统的矢量控制方程组
2.1 基于等效旋转控制绕组的电压方程
利用沈阳工业大学王风翔、张风阁、王正等提出的基于等效旋转控制绕组磁场定向矢量控制的数学模型[5-6],将其磁链方程代入电压方程,经过整理得出式(2):
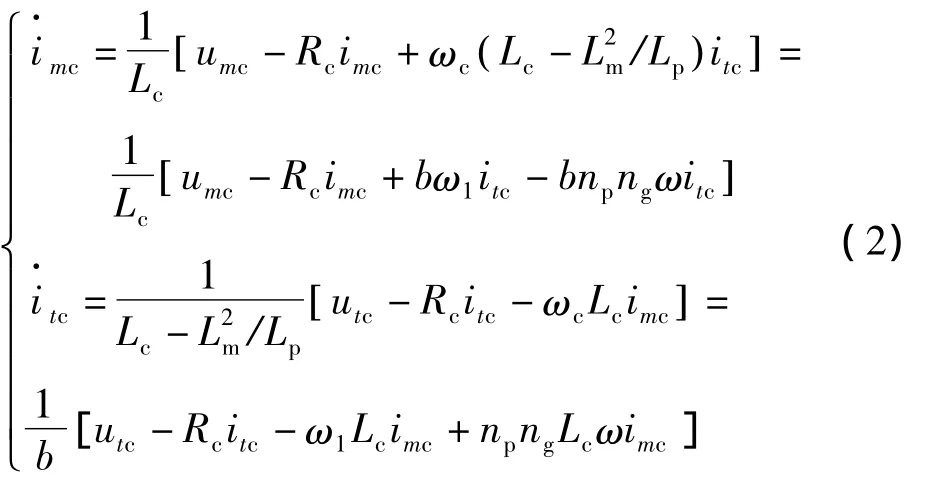
其中:u,i——电压和电流,其下标第1个字母代表m、t轴分量,第2个字母p、c代表功率绕组、控制绕组;
Rp,Rc——绕组的电阻;
Lp,Lc,Lm——绕组的自感及互感;
b=Lc-L/Lp;
ωp,ωc——绕组的电流角频率;
ω1——电网电压角频率;
ωr,ω——发电机、风力机机械角频率;
ng——齿轮箱增速比,ng= ωr/ω。
并网运行时,ωp=ω1,ωc=ωp-npωr=ω1-npngω。
2.2 转子运动方程
式(3)为折算到风力机侧的转子运动方程[7]:

式中:TM——风能转换为轮毂上的机械转矩。
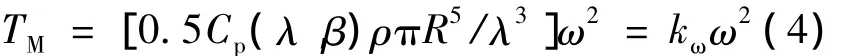
其中:kω=0.5Cp(λ,β)ρπR5/λ3;
ρ——空气密度;
R——风力机桨叶半径;
Cp(λ,β)——风力机的风能利用系数;
β——桨距角;
λ——叶尖速比,λ =ωR/υ;
υ——风速。

2.3 风力发电系统的整体方程组
式(2)、式(3)合并为无刷双馈型风力发电系统的状态方程,它是一组非线性、强耦合方程组,状态变量为 x=[θ ω imcitc]T,控制变量为[umcutc]T。目的是:利用式(2)、式(3)设计一个具备参数摄动镇定性能和干扰抑制性能的H∞鲁棒控制器,使得并网后的风力发电系统在不确定参数和不同风速作用下,保证风力机控制绕组电流励磁分量imc、转矩分量itc和有功功率仍能按预期的轨迹运行,以满足最大风能捕获和输出恒频恒压电能的要求。
3 直接反馈线性化
直接反馈线性化是中国学者提出并发展起来的基于系统输入-输出描述的一种反馈线性化方法[8],可将非线性系统在全局范围内进行线性化处理[9-10]。与基于微分几何理论的线性化方法对比,采用了不同的描述方式和处理方法,得到相同的线性化效果。直接反馈线性化的优点是所用的数学工具简单、物理概念清晰,适合于工程应用。
对式(2)、式(3)进行坐标变换,采用状态变量的偏差量为输出变量,得出输出方程:

式中:θref,ωref,imcref,itcref为选定的参考值。将式(5)对t求导得:
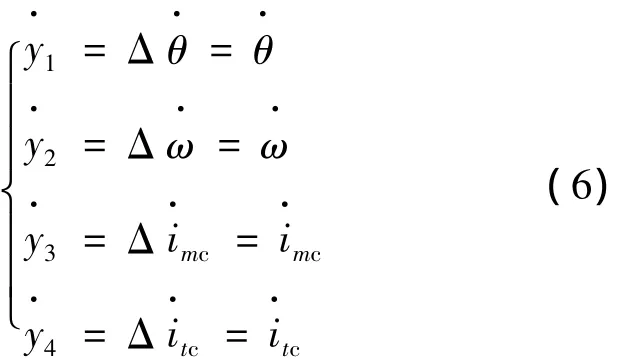
将不确定参数Rc,B,K用标称值和偏差值之和表示(温度变化引起Rc的偏差,转速变化和转轴的柔性变化引起B,K的偏差):

将式(5)~式(7)代入式(2)、式(3),得出具有参数摄动阵ΔA(t)和有界扰动w的不确定系统:

其中:x=[ΔθrΔωrΔimcΔitc]T

B1w包含非线性内容,代入参数的数值后,可估计出其上界w[11]。
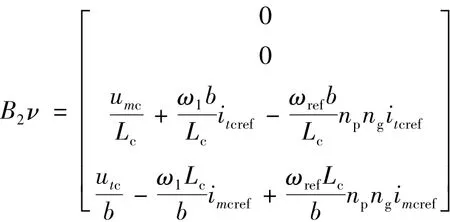
设 B2ν 第 3、4 行分别等于 ν1,ν2,它们被称为虚拟控制变量,即

4 H∞控制器的求解
式(8)符合参数不确定系统的H∞控制标准形式[12],第1式为被控对象,其中 ΔA(t)为参数摄动阵,可描述为
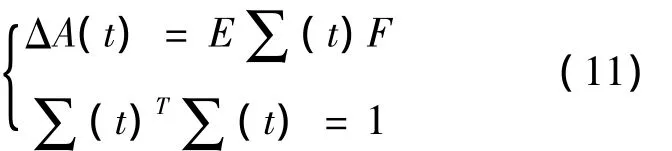

可用于求解具有鲁棒稳定、干扰抑制性能的状态反馈控制器。式(12)中:ε>0,ε越小,意味着系统对干扰抑制性能越好,但过小的ε将会削弱系统的鲁棒稳定性;D11为零矩阵。
式(8)的状态反馈控制器为

式中K为反馈系数,可以用求解Riccati不等式的方法或利用MATLAB软件中μ-分析与综合工具箱的hinffi.m函数求取。
由式(9)、式(13)可得出无刷双馈风力发电系统的非线性H∞控制律:

5 算例及计算机仿真
无刷双馈型风力发电系统参数如下:P1=3 kW,Up=220 V,fp=50 Hz,pp=3,pc=1,Rp=0.87 Ω,Rc=2.28 Ω,Lp=42 mH,Lc=37 mH,Lm=35 mH,风力机桨叶半径 R=4 m,J=500 kgm2,BN=3,KN=2,np=4,ng=7.8。在运行过程中,不确定参数Rc,B,K变化可达其标称值±30%。额定风速 υr=9 m/s,空气密度 ρ=1.25 kg/m3。设计H∞控制器并进行计算机数字仿真。
取 θref=0,ωref=10.3 rad/s,imcref=5 A,itcref=7 A;取可能发生的最大偏差值:p1=0.68 Ω,p2=0.9,p3=0.6。由式(2)、式(3)的说明,计算得:b=0.007 8 H,d=18.2。计算式(8)的各项系数,按式(11)指定 E,F,取式(12)中 ε =100。


选定加权函数 C1和 D12,由式(2)、式(3)、式(16)构成仿真模型来进行加权函数的优化。

求得状态反馈控制器的反馈系数K:

得上述无刷双馈型风力发电系统的H∞反馈控制律为

不失一般性,给出下列运行情况作为例子进行仿真:设不确定参数Rc=2.28±0.684 Ω,B=3+0.9sin 2t,K=2+0.6sin 3t;随着风速变化风力机的转速曲线如图2所示,发电机输出的有功功率指定为1.2 kW。
图3给出了当系统具有以上参数摄动和扰动时的仿真曲线。图3(a)为风力发电机输出有功功率,图3(b)、(c)分别为发电机控制绕组 m,t轴分量电流,实线为响应值,虚线为期望值。图4分别为H∞控制器的输出电压umc、utc。
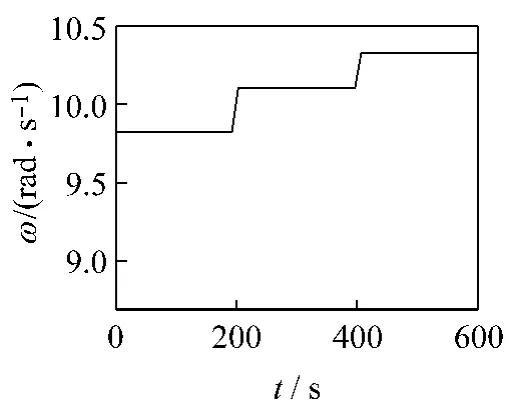
图2 无刷双馈型风力发电机的转速ω

图3 发电机有功功率、控制绕组m,t轴分量电流的响应值及期望值
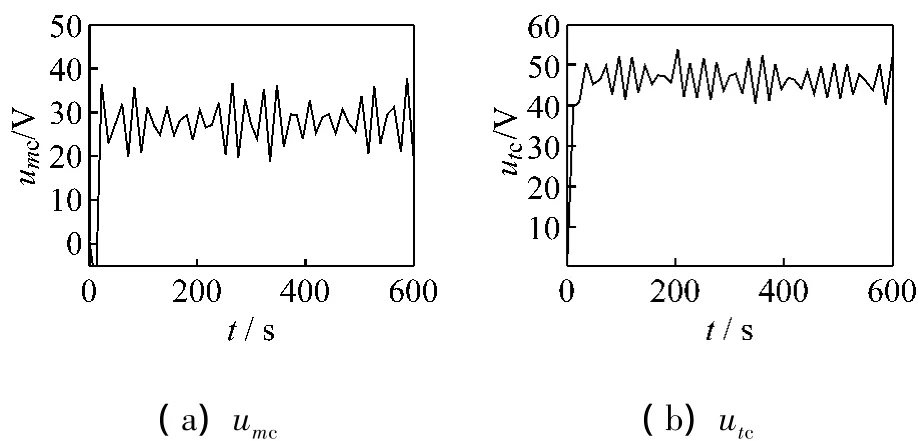
图4 H∞控制器的输出电压
从仿真结果可以看出系统具有很好的跟踪性能,实际响应值跟踪期望值,不受不确定参数和风速变化的影响。
6 结语
本文对无刷双馈型风力发电机的H∞控制进行了研究,建立了无刷双馈风力发电机的鲁棒控制模型,根据H∞控制理论,利用MATLAB工具箱设计了H∞控制器。仿真结果表明,在该控制器作用下,无刷双馈型风力发电机具备参数摄动镇定性能和干扰抑制性能,在系统参数不确定的情况下,风速变化虽然使风力发电机的转速随之变化,但输出的有功功率、控制绕组m,t轴分量电流的实际响应值仍能很好地跟踪期望值,安全可靠地获取最大风能,向电网输送恒频恒压的电能。
[1]张先勇,舒杰,吴捷.无刷双馈风力发电机组的自抗扰功率解耦控制[J].太阳能学报,2008,29(12):1477-1483.
[2]黄守道,王耀南,王毅,等.无刷双馈电机组有功和无功功率控制研究[J].中国电机工程学报,2005,25(4):88-93.
[3]王琦,陈小虎,纪延超,等.基于双同步坐标的无刷双馈风力发电系统的最大风能追踪控制[J].电网技术,2007,31(3):82-87.
[4]张先勇,吴捷,杨俊华.无刷双馈风力发电机滑模功率解耦控制[J].太阳能学报,2007,28(1):68-73.
[5]金镭.基于等效旋转控制绕组的无刷双馈电机控制策略研究[D].沈阳:沈阳工业大学,2007.
[6]王正.转差频率旋转坐标系的无刷双馈电机数学模型与矢量控制研究[D].沈阳:沈阳工业大学,2006.
[7]任丽娜,焦晓红,邵立平.双馈型变速恒频风力发电系统的鲁棒控制[J].控制理论与应用,2009,26(4):377-382.
[8]高龙.非线性系统的DFL及隐动态[J].清华大学学报,1996,36(9):1-9.
[9]张春朋,林飞,宋文超.基于直接反馈线性化的异步电动机非线性控制[J].中国电机工程学报,2003,23(2):99-102.
[10]蔡超豪.矢量控制异步电动机的非线性H∞控制[J].中小型电机,2004,31(1):49-52.
[11]丁刚,王勋先,韩曾晋.感应电机的H∞抗干扰控制[J].控制理论与应用,1999,16(4):483-486.
[12]申铁龙.H∞控制理论及应用[M].北京:清华大学出版社,1996:136-151.
