基于功率谱法分析场地效应对大跨度连续刚构桥的影响

熊 欢，张 犇，魏陆垚，王子健

（1.中铁二院武汉勘察设计研究院有限责任公司，湖北武汉 430071;2.重庆市市政设施管理局，重庆 401147;3.重庆交通大学 土木建筑学院，重庆 400074）

基于功率谱法分析场地效应对大跨度连续刚构桥的影响

熊 欢1，张 犇2，魏陆垚3，王子健3

（1.中铁二院武汉勘察设计研究院有限责任公司，湖北武汉 430071;2.重庆市市政设施管理局，重庆 401147;3.重庆交通大学 土木建筑学院，重庆 400074）

以一座全长为346 m的预应力混凝土连续刚构桥为基础，建立全桥计算模型，采用由规范反应谱生成的相应的功率谱，分6种工况对桥梁进行激励;通过多点激励与一致激励的对比，分析了场地效应对连续刚构桥的影响。结果表明:对于高墩大跨度连续刚构桥，场地效应主要对跨中截面不利，并使桥墩墩底内力产生突变。

反应谱;功率谱;场地效应;多点激励

近年来，大跨径桥梁被广泛建造，并做为重要的公众设施而存在，其在地震中的安全性始终是工程界和学术界十分关注的问题。由于地震发生的不确定性和传播机理的复杂性，传统的抗震分析方法很难应付［1-3］。合理的抗震设计必须对地震动的随机性和空间变化性给于充分的认识，导致地震动空间变化的因素主要包括:行波效应、场地效应、衰减效应和相干效应［4］。随着计算机技术的发展和人们对地震动认识的逐渐加深，多点激励成为国内外学者研究的热点［5-7］。范立础，等通过分析大跨度斜拉桥在非一致地震激励下的响应特征，指出局部土场地条件对斜拉桥的地震反应有重要影响，当各塔、墩处的土质差异较大时需进行详细的抗震分析［5］。项海帆和陈幼平分别以天津永和桥为例，分析了行波效应对连续刚构桥的影响，得出得研究结论却相差很大［6］。笔者以一座全长346 m的高墩大跨度连续刚构桥为基础，建立全桥模型，采用由反应谱生成的功率谱对该桥进行多点激励，分析了场地效应对连续刚构桥的影响。

1 功率谱与反应谱的转换公式

我国地震工程界经过多年努力，建立一套适合我国的地震加速度反应谱的规定，制订《公路桥梁抗震设计细则》，规定中采用场地系数考虑了场地类型对反应谱最大值的影响。但反应谱法难以处理地震动的空间效应对桥梁的影响，用功率谱法处理更为直接。然而，我国却并未建立一套合适的功率谱规定，面对量大面广的桥梁抗震设计，不可能请专业人员一一勘测确定。所以使用由地面加速度反应谱生成相应的地面加速度功率谱是比较现实的方法［8］。

1978 年，Kaul假定地面加速度为零均值高斯平稳随机过程，并假定单质点弹性体系的加速度反应的峰值超过一定界限的次数为泊松过程，得到其最大绝对值在［0，T］时间内的概率分布函数为［9-10］:

最大绝对值的概率密度为:

假定功率谱在p=ω附近变化缓慢，做如下转化:

最后可得到:

式（8）比较简单，且在一定的频率范围内具有较高的精度，但由于推导过程中采用了一些假设，因而其适用范围受到了限制。Kaul建议取p=0.85，但在实际应用中，发现其精度并不能令人满意，林家浩，等［9］建议将p取0.5，实际也证明计算精度得到极大的改善。《桥梁抗震细则》将该公式纳入规范，其中p=0.5，将式（8）稍做修改得:

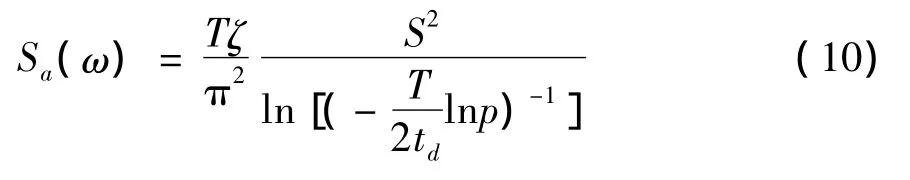
2 工程实例

某桥桥跨布置为（90+166+90）m预应力混凝土连续刚构桥，该桥立面如图1。场地属中软场地类型，即III类场地，抗震设防烈度为7度。利用ANSYS有限元软件建立全桥计算模型，采用solid65单元模拟混凝土，link 8单元模拟预应力束。有限元模型见图2，自振频率见表1。

表1 自振频率Tab.1 Natural frequency /Hz

3 地震功率谱分析

采用功率谱法对连续刚构进行场地效应的分析，参照文献［11］，取 I、II、III类场地的反应谱并依据式（10）计算相应的功率谱，其中III类场地的反应谱和相应的功率谱曲线如图3、图4。考虑地震动的场地效应，对连续刚构进行多点激励分析和一致激励分析，分别考虑以下6种工况:

工况A:一致激励分析，1#墩和2#墩的场地类别为I类;

工况B:一致激励分析，1#墩和2#墩的场地类别为II类;

工况C:一致激励分析，1#墩和2#墩的场地类别为III类;

工况D:考虑场地效应的多点激励，1#墩和2#墩的场地类别分别为III类和I类;

工况E:考虑场地效应的多点激励，1#墩和2#墩的场地类别分别为III类和II类;

工况F:考虑场地效应的多点激励，1#墩和2#墩的场地类别分别为II类和I类。位移峰值出现中跨跨中，而且相对一致激励放大2.3 ～5.6 倍。

4 计算结果及分析

4.1 场地效应对连续刚构桥主梁位移的影响

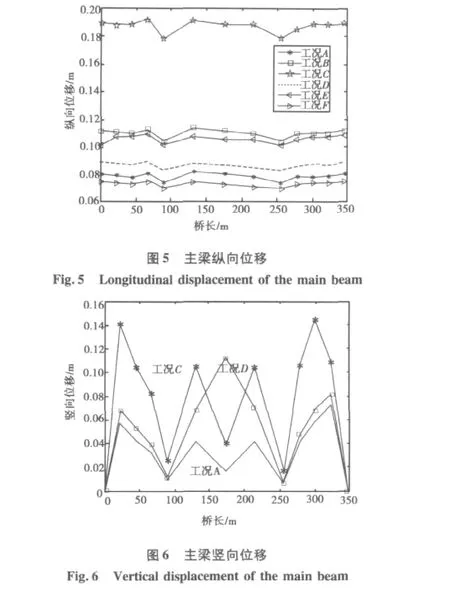
连续刚构桥主梁在6种工况中的纵向位移和竖向位移如图5、图6。

1）一致激励下，通过工况A、B、C相比较，当结构基础的场地条件从软土（工况C）换到基岩（工况A）时，主梁结构在纵向和竖向的位移减小。

2）通过工况D与工况A和工况C对比，多点激励作用下主梁纵向的位移大于场地条件为基岩时的一致激励下的位移，而小于场地条件为软土时的一致激励下的位移。

3）通过工况E与工况B、工况C对比、工况F与工况A、工况B对比，多点激励作用下主梁纵向位移小于一致激励下的位移。

4）一致激励下，连续刚构桥中跨跨中位移相对边跨跨中位移比较小，在多点激励作用下，桥梁竖向

4.2 场地效应对连续刚构桥桥墩位移的影响

桥墩在6种工况中的的纵向位移和竖向位移如图7、图8。

1）一致激励下，通过工况A、工况 B、工况C相比较，当结构基础的场地条件纵软土（工况C）换为基岩（工况A）时，桥墩纵向位移和竖向位移减小。

2）通过工况D与工况A和工况C相比较、工况E与工况B、工况C相比较、工况F与工况A、工况B相比较，多点激励作用下桥墩纵向位移和竖向位移均小于一致激励下的位移。

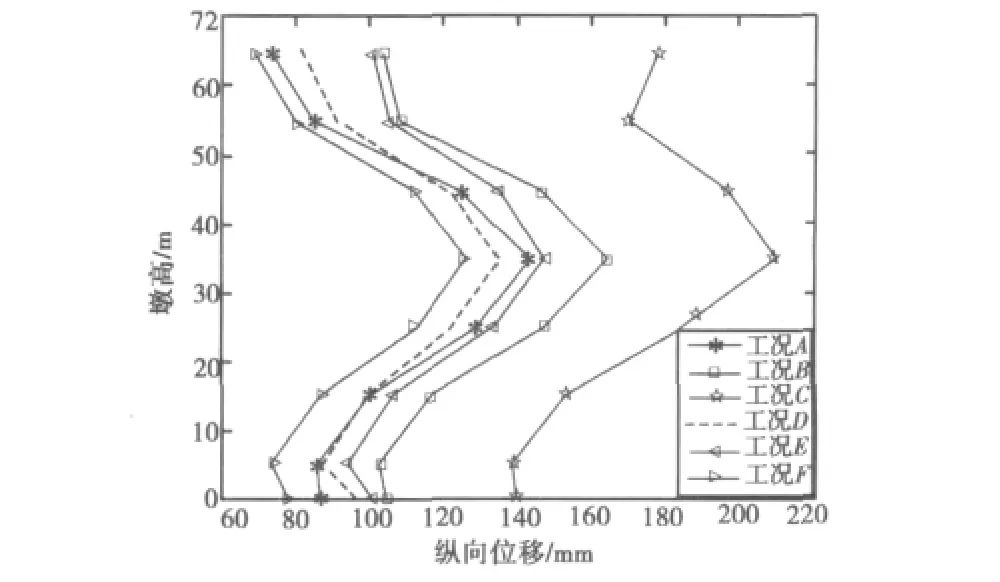
图7 桥墩纵向位移Fig.7 Longitudinal displacement of piers

图8 桥墩竖向位移Fig.8 Vertical displacement of piers

4.3 场地效应对连续刚构桥主梁内力的影响

对连续刚构桥进行多点激励和一致激励，分别提取图9中连续刚构桥的15个截面的弯矩和轴力，如表2。

图9 主梁截面Fig.9 Cross-section of the girder

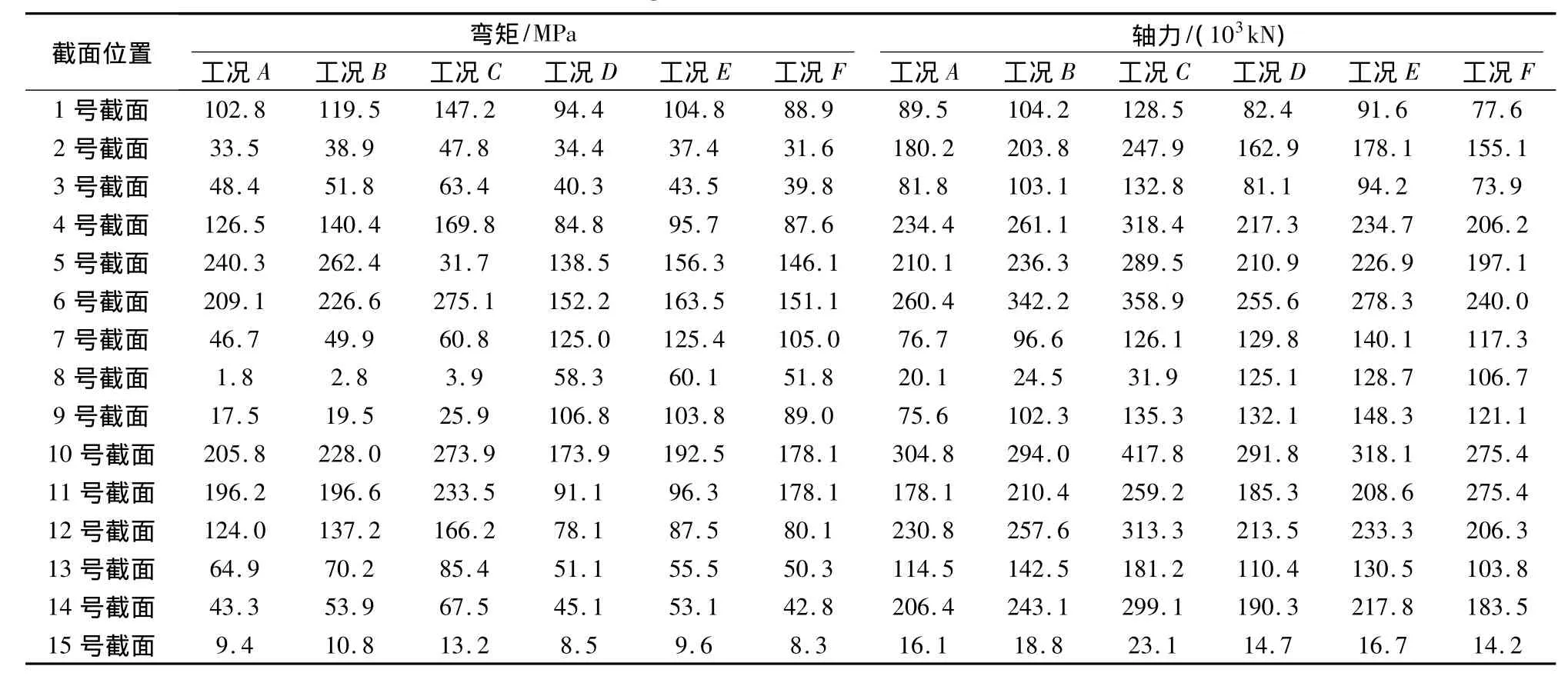
表2 主梁弯矩和轴力Tab.2 The bending moment and axial force of the cross-sections

1）一致激励下，通过工况A、工况B、工况C相比较，当结构基础的场地条件从软土（工况C）换为基岩后（工况A）时，主梁各截面的弯矩减小。

2）通过工况D与工况A和工况C相比较、工况E与工况B、工况C相比较、工况F与工况A、工况B相比较，多点激励下，跨中弯矩为一致激励下的14.6～32倍，场地效应对跨中弯距有放大作用。

3）通过工况D与工况A和工况C相比较、工况E与工况B、工况C相比较、工况F与工况A、工况B相比较，多点激励下主梁在边跨各截面的剪力小于一致激励下的截面剪力

4）通过工况D与工况A和工况C相比较、工况E与工况B、工况C相比较、工况F与工况A、工况B相比较，多点激励下，跨中轴力为一致激励下4.04 ～6.22 倍。

4.4 场地效应对连续刚构桥桥墩内力的影响

1号桥墩在6种工况中的的弯矩值和轴力值如表3。

表3 1号桥墩弯矩和轴力值Tab.3 The bending moment and axial force of the No.1 pier

1）一致激励下，当场地条件为软土时，桥墩各截面内力（弯矩、剪力、轴力）最大，当场地条件为基岩时，桥墩各截面内力（弯矩、剪力、轴力）最小。

2）通过工况D与工况A和工况C相比较、工况E与工况B、工况C相比较、工况F与工况A、工况B相比较，多点激励作用下桥墩的内力均小于一致激励下桥墩的内力。

3）通过工况D与工况A和工况C相比较，多点激励下，1号墩的响应相对较接近工况A的响应，这是因为连续刚构桥连接刚度较大，由2号墩传来的地震动激励作用，不可忽视。

4）多点激励下桥墩底部截面的内力（弯矩、剪力、轴力）产生突变，为一致激励下桥墩内力2～4倍。

5 结论

1）通种6种工况对比，连续刚构桥在场地条件为软土时一致激励下的位移和内力反应均为最大。

2）多点激励下，全桥的纵向位移和竖向位移相对于一致激励减小，但场地效应对主梁跨中的竖向位移放大2.3 ～5.6倍。

3）多点激励下，主梁的内力相对一致激励会减小，但场地效应会使主梁跨中的弯矩和轴力分别放大14.6～32倍和4.04～6.22倍，所以场地效应主要对跨中截面不利。

4）多点激励作用下桥墩的内力（弯矩、剪力、轴力）均小于一致激励下的内力，但在墩底内力产生突变，约为一致激励下桥墩内力（弯矩、剪力、轴力）2～4倍。

（References）:

［1］ 苗家武，胡世德，范立础.大型桥梁多点激励效应的研究现状与发展［J］.同济大学学报，1999，27（2）:189-193.

MIAO Jia-wu，HU Shi-de，FAN Li-chu.Actual research state and development of study on seismic performance of long span bridges under multiple-support excitation［J］.Journal of Tongji University，1999，27（2）:189-193.

［2］ 李建俊，林家浩，张文首，等.大跨度结构受多点随机地震激励的响应［J］.计算结构力学及其应用，1995，12（4）:445-450.

LI Jian-jun，LIN Jia-hao，ZHANG Wen-shou，et al.Responses of long-span structures subjected to arbitrarily coherent multi-point stationary random seismic excitation［J］.Computational Structural Mechanics and Applications，1995，12（4）:445-450.

［3］ 林家浩，张亚辉，赵岩.大跨度结构抗震分析方法及近期进展［J］.力学进展，2001，31（3）:350-360.

LIN Jia-hao，ZHANG Ya-hui，ZHAO Yan.Anti-seismic analysis methods and recent advances of long-span structures［J］.Advances in Mechanics，2001，31（3）:350-360.

［4］ 赵岩.桥梁抗震的线性/非线性分析方法研究［D］.大连:大连理工大学，2003.

［5］ 范立础，王君杰，陈玮.非一致地震激励下大跨度斜拉桥的响应特征［J］.计算力学学报，2001，18（3）:358-363.

FAN Li-chu，WANG Jun-jie，Chen Wei.Response characteristics of long span cable-stayed bridges under non-uniform seismic action［J］.Chinese Journal of Computational Mechanics，2001，18（3）:358-363.

［6］ 陈幼平，周宏业.斜拉桥地震破坏的计算研究［J］.地震工程与工程振动，1995，15（3）:127-134.

CHEN You-ping，ZHOU Hong-ye.Seismic damage and collapse of cable-stayed bridges［J］.Earthquake Engineering and Engineering Vibration，1995，15（3）:127-134.

［7］ 赵灿晖，周志祥.大跨度上承式钢管砼拱桥的地震响应分析［J］.重庆交通大学学报:自然科学版，2007，26（5）:1-4.

ZHAO Can-hui，ZHOU Zhi-xiang.Seismic response analysis of long span CFST deck-type arch bridges［J］.Journal of Chongqing Jiaotong University:Natural Science，2007，26（5）:1-4.

［8］ 单德山，李乔.高墩深水大跨度连续刚构桥非一致地震响应分析［J］.重庆交通大学学报:自然科学版，2008，27（4）:499-501.

SHAN De-shan，LI Qiao.Seismic response analysis of long-span continuous rigid-framed bridge with high-rise piers in deep water under non-uniform seismic excitation［J］.Journal of Chongqing Jiaotong University:Natural Science，2008，27（4）:499-501.

［9］ 林家浩，张亚辉.随机振动的虚拟激励法［M］.北京:科学出版社，2004.

［10］张亚辉，陈艳，李丽媛，等.桥梁抗震随机响应分析及输入功率谱研究［J］.大连理工大学学报，2007，47（6）:786-792.

ZHANG Ya-hui，CHEN Yan，LI Li-yuan，et al.Seismic random vibration of bridges and input power spectrum analysis［J］.Journal of Dalian University of Technology，2007，47（6）:786-792.

［11］JTG/TB 02-01—2008公路桥梁抗震设计细则［S］.北京:人民交通出版社，2008.

Influence on Long-span Continuous Rigid Framed Bridge of Site Effect Based on Power Spectrum Method

XIONG Huan1，ZHANG Ben2，WEI Lu-yao3，WANG Zi-jian3
（1.Wuhan Survey and Design Institute Co.，Ltd.of CREEC，Wuhan 430071，Hubei，China;
2.Chongqing Municipal Inprastructure Administrafion Bureau，Chongqing 401147，China;
3.School of Civil Engineering and Architecture，Chongqing Jiaotong University，Chongqing 400074，China）

A computing model of the entire bridge was established based on a prestressed concrete continuous rigid framed bridge，which was 346m.The bridge was to be excited under six working conditions respectively using the power spectrum generated from standard response spectrum.By compared multi-support excitation with uniform excitation，this essay analyses the influence of site effect on continuous rigid framed bridge.The research result indicates that for continuous rigid framed bridge of high piers and long span，site effect is mainly disadvantageous to the mid-span cross-section of girders，and can cause a abrupt change of internal force of the bottom of piers.

response spectrum;power spectrum;site effect;multi-support excitation

U448

A

1674-0696-（2011）04-0712-05

10.3969/j.issn.1674-0696.2011.04.002

2011-04-26;

2011-05-09

国家自然科学基金项目（50879097）

熊 欢（1986-），男，湖北荆州人，硕士，主要从事桥梁抗震方面的研究工作。E-mail:xionghuan000@163.com。