正交流形保持投影方法

张 伟，夏利民，罗大庸

(中南大学 信息科学与工程学院，湖南 长沙，410075)

特征提取是模式识别领域中一个重要的研究方向，人们已经提出了很多特征提取方法，其中最经典的一种就是主分量分析(PCA)[1]。它是寻找使均方误差最小的线性最优变换矩阵，并且最优矩阵由样本方差的最大特征向量(叫做主分量)组成。PCA的目标是尽可能地保留样本的方差信息。但用PCA进行特征降维时，经常无法保留数据中的非线性结构，而这些非线性特性对于物体的识别是非常重要的。最近，提出了一种新的特征提取方法，即保局投影(LPP)[2-3]，它具有较强的流形学习能力，当数据存在非线性结构时，该方法能很好地保留图像的非线性特征。LPP的目标是尽可能地保留数据的局部流形结构，它通过使近邻样本之间的欧几里德距离最小来寻找最优投影方向。然而，LPP存在一些缺陷：非正交变换；没有利用数据非近邻信息，因此，在投影过程不一定能保持数据全局流形结构。针对这些问题，人们已提出了一些改进的算法[4-14]，如Yang等[4]提出了非局保留投影(NLPP)，寻找使非近邻样本的欧几里德距离最大的最优投影方向，这种方法有效地利用了数据的非近邻信息，但只适合非近邻特性起主导作用的情况；韦佳等[5]利用全局信息、局部信息正、负约束信息提出了基于局部与全局保持的半监督维数约减方法。Cai等[6]在特征值求解过程中增加了正交约束，提出了正交局部保持投影方法(OLPP)，但该方法计算相当复杂。李瑞东等[7-8]利用Schur分解，提出了基于Schur分解的正交鉴别局部保持投影方法。Zhu等[9]利用投影基向量变换，提出了正交局部保持投影方法。本文作者针对LPP的缺陷，提出一种正交流形结构保持投影方法(OMPP)，在 LPP目标函数中引入非近邻信息，与保局投影相比，改进后的方法能更好地保持数据的局部流形结构和全局结构；采用格拉姆-施密特正交化过程(Gram-Schmidt orthogonalization)[14]获得正交投影向量，解决了保局投影非正交问题。在ORL和Yale人脸数据库上进行实验，实验结果验证了该算法的有效性。

1 保局投影LPP

LPP算法本质上是一种线性降维方法，根据最近邻图来建立映射，设在高维欧式空间 Rn中有数据集X={x1, x2, …, xN}，寻求一个投影矩阵A，将这些数据映射到一个相对低维的特征空间 Rd(d≤n)中。数据集在Rd中的表述为Y={y1, y2, …, yN}，且Y=ATX。

LPP算法的目的是在特征降维的同时，保持样本固有的局部流形结构不变。LPP的准则函数为：

在下列约束条件下，使目标函数J1最小的A就为LPP的投影矩阵A：

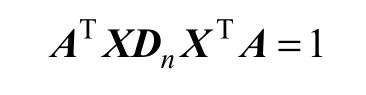
可证明，目标函数J1极小化问题就是下面的广义特征值求解问题：

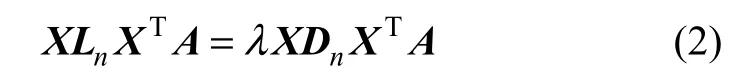
即方程(2)前 d个最小的特征值对应的特征向量 a1,a2, …, ad组成矩阵A。

很显然，经过保局投影，高维空间距离很近的 2个点的低维投影点之间的距离也应该很近，即保局投影能有效地保持样本固有的局部流形结构不变。但是LPP存在下列问题：

(1) LPP不能保证在投影过程中保持数据全局流形结构，因为没用考虑数据非近邻信息。

(2) LPP不是正交变换。因为 ( XDnXT)-1XLnXT不一定是对称的，所以，特征向量a1, a2, …, ad不一定正交。

为了有利于数据的分类，希望数据集经过投影后，高维空间相邻的点在低维空间也接近，而非邻近点在低维空间应该尽量散开；同时，希望消除数据各分量之间的相关性，因此，要求投影变换是正交投影。而这些是保局投影无法保证的。为此，作者提出了改进的保局投影，即正交流形保持投影。

2 正交流形保持投影

2.1 流形保持投影

对于非邻近点，定义：

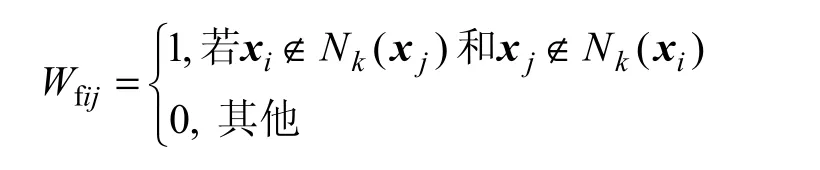
要使非邻近点的低维投影能够尽量散开，则要求下列目标函数应最大：

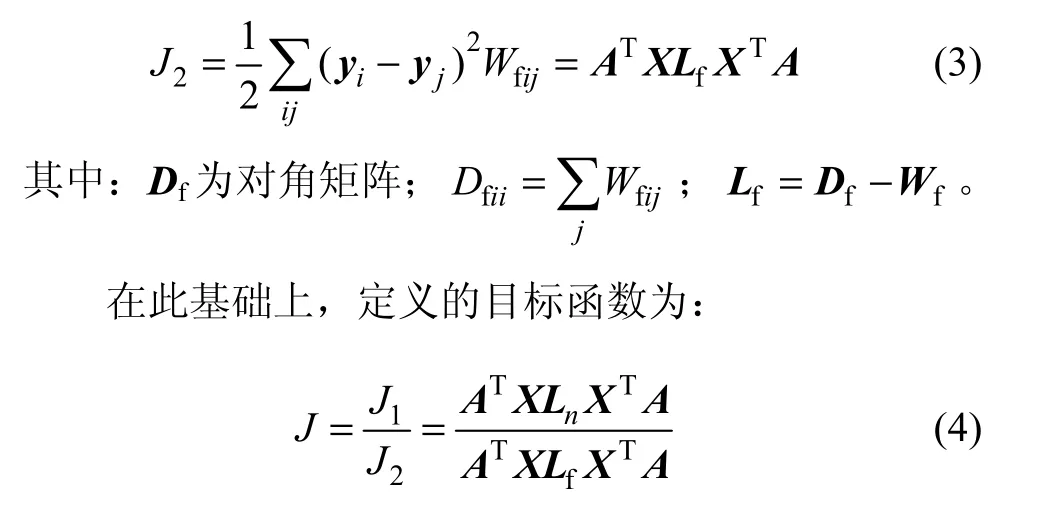
要使投影后邻近点的低维投影点很近，当非邻近点的低维投影点离得很远时，应保持数据的局部流形结构和全局结构不变，则要求目标函数J最小。这种投影称为流形保持投影。

若XLfXT是非奇异的，则求目标函数最小的问题转化为求下列广义特征值问题：

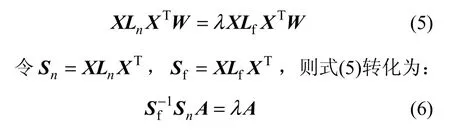
方程(6)前 d个最小的特征值对应的特征向量 a1,a2, …, ad组成投影矩阵A=(a1, a2, …, ad)。

2.2 正交流形保持投影

由于a1, a2, …, ad为非正交向量，下面利用格拉姆-施密特正交化过程求方程(6)前 d个最小的特征值对应的正交特征向量a1, a2, …, ad。

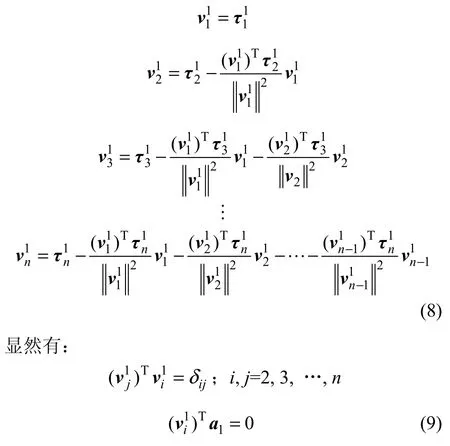
2.2.1 第1个正交特征向量a1

2.2.2 第2个正交特征向量a2

由于特征矢量a2满足=0和S-1Sa=λa，fn因此，a2必定在与第1个特征向量a1垂直的(n-1)维子空间Sn-1上，所以，应该在Sn-1上寻找=λa最小特征值对应的特征向量作为a2。

将矩阵Sn，Sf转化成Sn-1空间的矩阵：

2.2.3 第i个正交特征矢量ai(i =3, 4, …，d)

将矩阵Sn和Sf转化成空间的矩阵：

即特征向量a1, a2, …, ad是正交的。因此，A是正交投影矩阵，投影变换Y=ATX是正交投影。

3 实验与结果

为说明本文作者方法的有效性，在ORL和Yale 2种人脸数据库上进行实验，并与PCA，LPP，NLPP和OLPP等方法进行比较。

实验1在ORL标准人脸库上进行，此人脸库由40人、每人10幅图像组成，图像有112×92个像素。这些图像拍摄于不同时期，图像的特点是：(1) 表情不一，如：愤怒、 厌恶、 恐惧、高兴、平静、 悲伤、惊讶、眼睛睁与闭；(2) 脸部姿态不一，人脸深度旋转和平面旋转可达20°；(3) 佩戴物不一，如戴眼镜与不戴眼镜；(4) 人脸的尺度变化多达10%。图1所示是ORL人脸库中部分人脸图像。实验中，以每个人的前5幅图像作为训练样本，后5幅作为测试样本，训练样本和测试样本总数均为200。

首先对图像进行预处理，将图像剪辑、归一成为64×64像素。然后分别采用PCA，LPP，NLPP和OLPP及文中方法(OMPP)提取人脸特征；最后，用余弦距离来衡量样本之间的相似程度，采用最近邻分类器进行人脸识别。表1给出了这几种方法的最高识别率及对应特征维数。

实验2在Yale人脸库上进行。此人脸库由15人、每人11幅图像组成，图像像素为100×100。这些图像是在不同表情和光照条件下拍摄的。图 2所示是Yale人脸库中部分人脸图像。实验中，以每人的前6幅图像作为训练样本，后5幅作为测试样本，训练样本数为66，测试样本数为55。首先将图像剪辑、归一成为64×64像素。表2所示是PCA，LPP，NLPP，OLPP和OMPP方法加余弦距离下的最近邻分类器的最高识别率及对应特征维数。

图1 ORL人脸库中部分人脸幅图像Fig.1 Sample images in ORL database

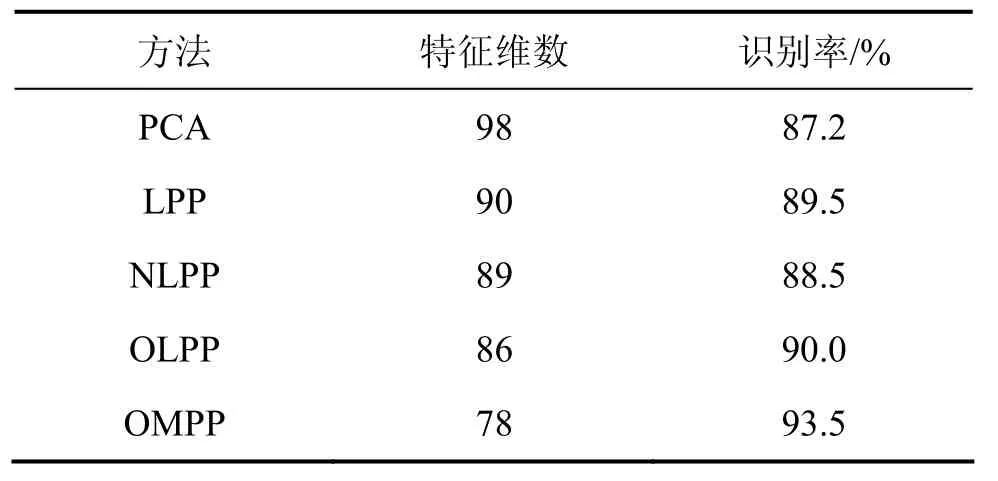
表1 在ORL人脸库上5种方法的识别结果Table1 Recognition results of five methods on ORL database

以上实验结果表明：OMPP方法的识别率与其他几种方法相比有明显提高，并且OMPP方法减少了表情、姿态、光照等因素对人脸识别的影响。其中PCA识别率最低，这是由于人脸图像存在大量的非线性结构，而这些非线性结构对于人脸识别十分重要。当使用PCA变换时，这些非线性结构经常无法保留，导致识别降低；LPP只考虑了数据的近邻信息，不能保持数据的全局流形结构，当使用LPP降维时，对于比较相似的人脸就可能难以分开；而NLPP只考虑了数据的非近邻信息，没有考虑近邻信息，因此，对于同一个人，当其表情、姿态或者光照发生较大变化时，采用NLPP很可能出现误识；OLPP利用了局部与全局信息，因此，识别率得到提高。作者提出的OMPP方法由于同时考虑了数据的近邻信息和非近邻信息，有效地保持了数据的局部流形结构和全局流形结构，使得识别率有了明显提高；同时，由于所得到的基向量具有正交性，消除了数据各分量之间的相关性，使得特征维数有了明显减少。

图2 Yale人脸库中部分人脸幅图像Fig.2 Sample images in Yale database

表2 在Yale人脸库上5种方法的识别结果Table2 Recognition results of five methods on ORL database

4 结束语

(1) 保局投影是一种非常有效的特征提取方法，针对LPP存在的缺陷，本文作者提出了正交流形保持投影方法。

(2) 在保局投影目标函数中引入数据的非近邻信息，有效地保持了数据的局部流形结构和全局流形结构；采用格拉姆-施密特正交化过程获取正交投影基向量，解决了保局投影非正交问题。

(3) 在ORL和Yale人脸数据库上进行实验，实验结果验证了该方法的有效性。

[1] Turk M, Pentland A P. Eigenfaces for recognition[J]. Journal of Cognitive Neuroscience, 1991, 3(1): 71-86.

[2] He X F, Niyogi P. Locality preserving projections[C]//Proceedings of 17th Annual Conference on Neural Information Processing Systems. Cambridge: MIT Press, 2003: 585-591.

[3] He X F, Yan S C, Hu Y X, et al. Face recognition using laplacianfaces[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(3): 328-340.

[4] YANG Jian, ZHANG David, YANG Jing-yu. Non-locality preserving projection and its application to palmprint recognition[C]// Proceedings of 9th International Conference on Control, Automation, Robotics and Vision. Piscataway: IEEE,2006: 1-4.

[5] 韦佳, 彭宏. 基于局部与全局保持的半监督雄数约减方法[J].软件学报, 2008, 19(11): 2833-2842.

WEI Jia, PENG Hong. Local and global preserving based semisupervised dimemsionality reduction[J]. Journal of Software,2008, 19(11): 2833-2842.

[6] Cai D, He F X, Han J W, et al. Orthogonal laplacianfaces for face recognition[J]. IEEE Transactions Image Process, 2006,15(11): 3608-3614.

[7] 李瑞东, 余党军, 陈偕雄. 一种新的正交保局投影人脸识别方法[J]. 科技通报, 2007, 23(5): 702-704.

LI Rui-dong, YU Dang-jun, CHEN Xie-xiong. A new alternative formulation of orthogonal LPP with application to face recognition[J]. Bulletin of Science and Technology, 2007, 23(5):702-704.

[8] 林宇生, 郑宇杰, 杨静宇. 一种基于Schur分解的正交鉴别局部保持投影方法[J]. 中国图像图形学报, 2009, 14(4):701-706.

LIN Yu-sheng, ZHENG Yu-jie, YANG Jing-yu. An orthogonal discriminant locality preserve projections with schur decomposition[J]. Journal of Image and Graphics, 2009, 14(4):701-706.

[9] Zhu L, Zhu S A. Face recognition based on orthogonal discriminant locality preserving projections[J]. Nurocomputing,2007, 70(7/9): 1543-1546.

[10] Shao J D, Gang R, Jong M L. Generalized orthogonal locality preserving projections for nonlinear fault detection and diagnosis[J]. Chemometrics and Intelligent Laboratory Systems,2009, 96(1): 75-83.

[11] 肖永良, 夏利民. 基于改进的保局投影视频特征提取[J]. 模式识别与人工智能, 2010, 23(3): 396-401.

XIAO Yong-liang, XIA Li-min. Video feature extraction based on improved locality preserving projections[J]. Pattern Recognition and Artificial Intelligence, 2010, 23(3): 396-401.

[12] He X F, Yan S C, Hu Y X, et al. Learning a locality preserving subspace for visual recognition[C]// Proceedings of 9th International Conference on Computer Vision. Los Alamitos:IEEE Comput Soc, 2003: 385-392.

[13] CHENG Jian, LIU Qing-shan, LU Han-qing, et al. Supervised kernel locality preserving projections for face recognition[J].Nurocomputing, 2005, 67(8): 443-449.

[14] Liu K, Cheng Y Q, Yang J Y. A generalized optimal set of discriminant vectors[J]. Pattern Recognition, 1992, 25(1):731-739.