电浮选过程中气泡行为的研究
2011-06-01汪朝晖廖振方陈德淑
汪朝晖,廖振方,陈德淑
(重庆大学 机械工程学院,重庆,400044)
浮选矿物时,气体介质的分散性和气泡粒径对浮选效率起着很大作用,叶轮式浮选机能获得的气泡直径一般为0.8~0.9 mm,真空浮选能获得的气泡直径一般为0.1~0.2 mm,在某些情况下。采用压缩空气气浮法也可得到直径为0.06~0.08 mm的气泡[1]。获得微小的气泡具有非常重要的意义,因为它们在矿物颗粒表面上具有非常大的活性,从而使小气泡黏浮矿粒的速度要比大气泡黏浮矿物的速度快得多。与传统的浮选矿物相比,电浮选兼有电渗析、电泳、电加工、电凝和电化学等作用,能获得更小的气泡直径,目前,它已作为天然原料中获取贵重金属的一个重要手段,大大提高了贵重金属的回收率,是一种很有前途的浮选方法[2-4]。电浮选过程中形成的气泡有如下特点:
(1) 电解时形成的气泡分散浓度高,微粒组分均质。根据电解条件的不同,可以获得直径为5~100 μm的气泡,这比机械式、气动力式浮选机以及真空浮选法所获得的气泡小1~2个数量级。浮选过程中的气泡在液体内所有物质上均匀分布,尽管电浮选时产生高浓度的气泡,但它的总体积要比浮选机所获得的空气泡的空气容积小100倍以上。
(2) 电解的微气泡直径很容易调节。改变电解液的参数、选择相应的电极几何尺寸和在浮选介质中确定所需的pH,就能在较大范围内平滑地改变气泡的分散特性。在浮选介质的单位体积内、浓度一定的条件下找出固相颗粒尺寸与气泡尺寸的比例关系,这样就能根据浮选浆中固相微粒的粒径建立最佳的浮选条件。
(3) 在微气泡的界面上存在有电荷。电浮选时由于电化学反应,产生H+和OH-,从而在电极上形成气相的氢和氧,气泡被它们所吸附。颗粒表面与电解产生的气泡相互作用可以增强气泡与固体颗粒之间的内聚现象,最适合用于分选微细物质。
(4) 电解气泡具有较高的物理化学活性。在电解过程中,释放的氢和氧使水溶液形成盐,酸和碱,电解气泡的高度活性为调节矿物组分和表面特性以及浮选浆液提供了重要手段,因此,能大大提高电浮选的效率。
目前,对电浮选分离微小固体物质缺乏系统的研究,在此,本文作者对电浮选过程中的气泡行为进行分析和探讨,以便为电浮选的大规模应用提供参考依据。
1 电浮选过程中的气泡特性方程
在电浮选过程中,液体分散相速度与气泡直径有着非常密切的关系[5-7]。气泡特性方程为:

式中:c1和c2分别自由粒子和气泡的浓度;k为液体分散相速度方程。
液体分散相的速度方程为:
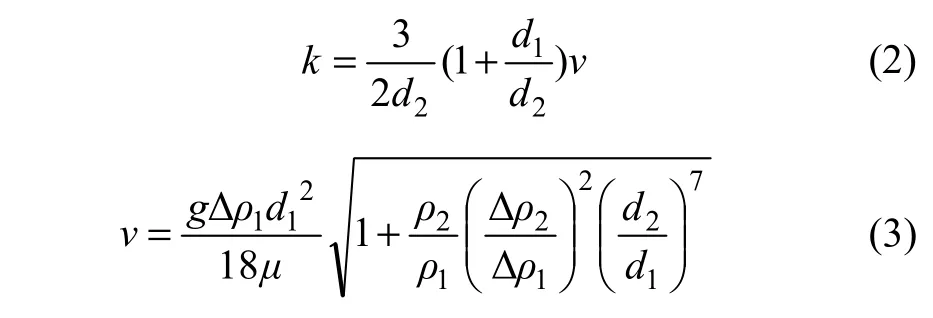
式中:d1和d2分别为自由粒子和气泡的直径;v为自由粒子的加权速度;ρ1和ρ2分别自由粒子和气泡的密度;Δρ1和Δρ2分别为自由粒子与水以及气体与水的密度差;μ为气泡的黏度。
由式(2)可知,速度方程是气泡直径的函数,对它取极值得:

显然,式(5)将液体分散相的物理特性和气泡的几何尺寸用数学表达式联系起来。
2 影响气泡直径的主要因素
由于电极电位的改变,正极或负极的电化学极化作用都将对从电极脱离出来的气泡直径产生很大影响。电流密度、介质的pH、电极材料、电极直径和温度等对电极极化作用的改变具有重要的影响[8-9]。本试验中,为了更好地研究影响气泡直径的主要因素,电极材料分别采用铂、铜、锡、银、不锈钢丝和石墨丝,其直径变化范围为0.2~1.0 mm,电流密度变化范围为10~40 mA/cm2,温度变化范围为 5~75 ℃,pH 用H2SO4,NaOH和Na2SO4来调配。试验中,在研究某一参数的影响时,其他所有参数都保持不变,采用高速摄影机(800~1 200帧/s)对试验过程进行观察。
气泡直径与电极材料的关系如图1所示,其中:电流密度均为25 mA/cm2,各种电极直径均为0.4 mm,温度均为20 ℃。从图1可以看出:气泡直径的变化有很明显的特点,在酸性介质中的氢气泡直径要比在中性介质和碱性介质中的氢气泡直径大,在中性介质中的电极材料和碱性介质中的铜、锡电极材料下,都能获得直径较小的气泡。
从图 1(a)可见:在特别强的酸性介质中,阴极材料对所产生的氢气泡直径有明显的影响,锡电极能获得较小直径的气泡,直径为20 μm的氢气泡的气泡量为20%;氢气泡直径有较宽的分布范围,石墨电极获得的气泡直径多为40 μm左右,气泡量为25%,而铂电极获得的气泡直径相对较大,直径在70 μm左右的气泡量为35%,气泡平均直径的偏差为50 μm。
在图1(b)可以看到,对于中性介质,从阴极释放出的氢气泡的直径与阴极材料并无太大关系,在气泡直径为15~25 μm的范围内均能获得较多的气泡。对于铂电极,能得到更多直径在15 μm左右的气泡,气泡直径分布比较集中,石墨电极能获得较多直径在25 μm左右的气泡,气泡的分布直径范围较宽,偏差达80 μm。
从图 1(c)可看出:对于碱性介质,阴极材料对氢气泡直径的影响较小,大部分气泡平均直径为 15~30 μm,锡电极能获得含量较高的小气泡,银电极获得的小气泡含量较少。
在铂电极上所形成的氧气泡直径与 pH关系如图2所示。从图 2可以看出:在酸性介质内,40%的氧气泡直径是25 μm;而在中性介质和碱性介质中,分别有38%和42%的氧气泡直径为30和55 μm。因此,随着介质 pH的增大,从阳极释放出的氧气泡直径也是显著增大的。这与从阴极释放出的氢气泡与介质pH的关系有明显的不同,但是,介质pH对氧气泡和氢气泡直径均有较大影响。
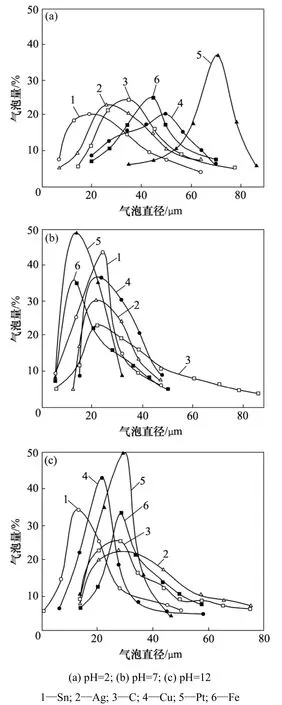
图1 电极材料(阴极)对氢气泡直径的影响Fig.1 Effects of electrode materials (negative electrode) on hydrogen bubble diameters
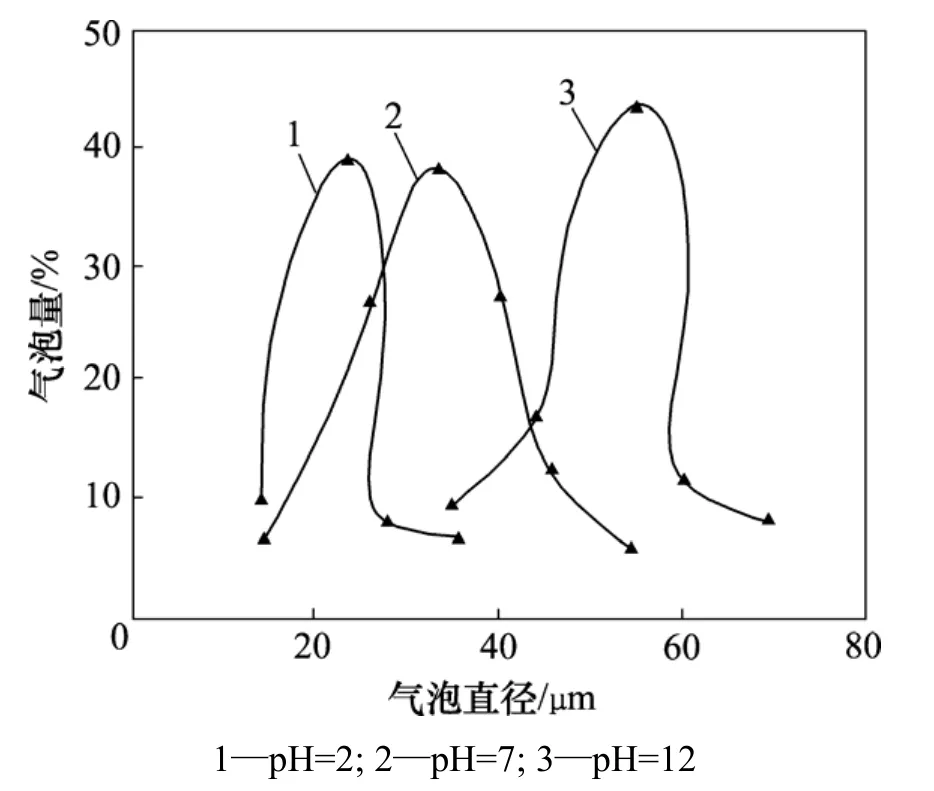
图2 铂电极(阳极)中pH对氧气泡直径的影响Fig.2 Effects of pH on oxygen bubble diameter for platinum electrode (positive electrode)
在电极直径分别为0.2,0.5和1.0 mm,电极材料均为铂,电流密度为25 mA/cm2,温度为20 ℃,pH为12时,电极直径对气泡直径的影响如图3所示。从图3可以看出:随着电极直径的增加,氢气泡和氧气泡的最大气泡量所对应的气泡直径增加不大,但是气泡直径变化的分散性比较明显;对于直径为 0.2 mm的电极,直径为20 μm的氢气泡占的气泡量为40%以上,气泡直径为15~45 μm;当电极直径为1.0 mm时,直径为40 μm的气泡量较多,此时,释放出的氢气泡最大直径增大到60 μm。对氧气泡而言,当电极直径为0.2 mm时,大多数氧气泡直径为40~60 μm,其中以直径为55 μm的气泡含量最大;当电极直径为1.0 mm时,气泡直径分布比较均匀,气泡量没有明显的变化。
图3 电极直径对气泡直径的影响Fig.3 Effects of electrode diameter on bubble diameter
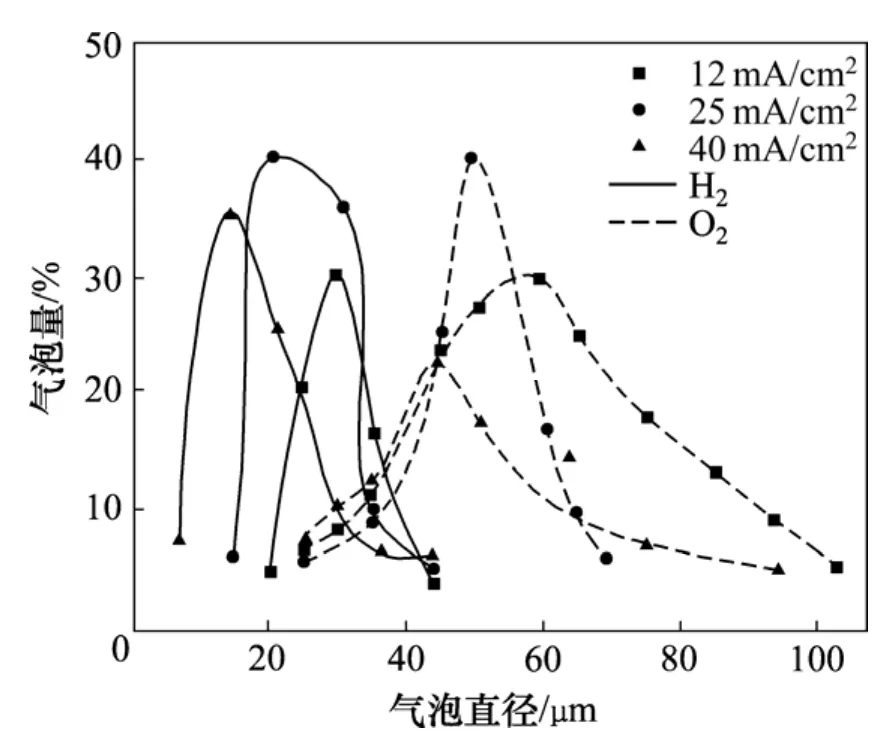
图4 电流密度对气泡直径的影响Fig.4 Effects of current density on bubble diameter
当电流密度分别为12,25和40 mA/cm2时,电极材料均为铂,电极直径为0.2 mm,温度为20 ℃,pH为12时,电流密度对气泡直径的影响如图4所示。从图4可以看出:随着电流密度的增加,最大气泡量所对应的氢气泡直径为 30~15μm;电流密度为 40 mA/cm2时,氢气泡直径普遍较小;当电流密度为 12 mA/cm2时,氢气泡的直径大部分为30 μm左右,但其直径分布变化较小。随着电流密度的增大,氧气泡直径的变化不是很明显,大部分氧气泡直径集中在45~60 μm,只是氧气泡直径的变化区间增大,在电流密度为 12 mA/cm2时,仅有小部分气泡直径超过100 μm。
当电极材料均为铂,电流密度为25 mA/cm2,pH为7,电极直径为0.5 mm时,温度在5,25,55和75 ℃时,氢气泡直径随温度变化的分布规律如图5所示。从图5可以看出:随着温度的增加,最大气泡量所对应的氢气泡直径有增加的趋势,在 5 ℃时为 25 μm,25 ℃时为 35 μm,55 ℃时为 45 μm,75 ℃时为50 μm,因此,温度对气泡直径的影响较大。但整个氢气泡的直径分布范围并未发生太大的改变,大部分氢气泡直径为 20~60 μm。
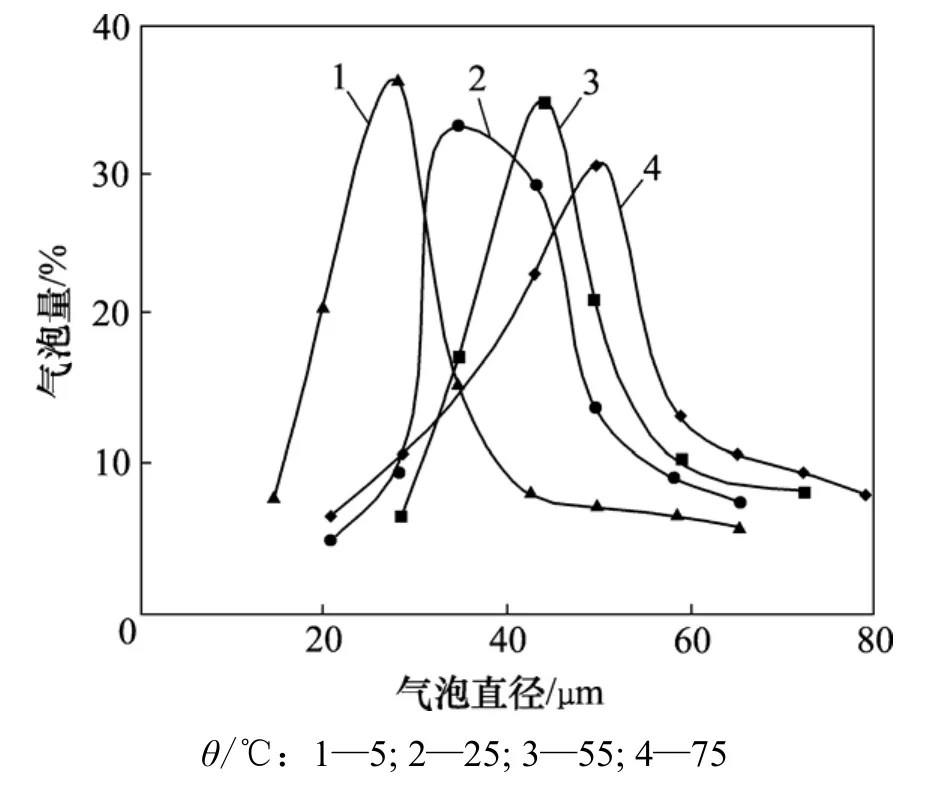
图5 温度对氢气泡直径的影响Fig.5 Effects of temperature on bubble diameter
3 粒子与气泡碰撞概率的确定
在粒子和气泡碰撞过程中,假设气泡和自由粒子相对于液流来说是层流的,液流速率为:

式中:v0和α为根据试验得到的常数。同时,可以认为气泡相对于液流的速率为:

而液流相对于粒子的速率为:

其中:D=(Di),为气泡的平均直径,它与电流密度的关系可用 D =D(1+e-βi)来拟合;d为粒子的平均直径;i为电流密度;b, b1,D0和β都是根据试验取得的参数。因此,气泡相对于粒子的运动速率为:
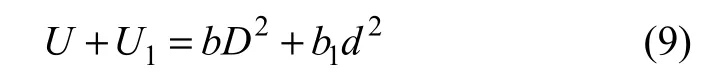
假设在一定的电浮室体内,气泡和粒子的浓度分别为n0和ξ,那么,1个粒子在t时间内可能发生的碰撞次数为:
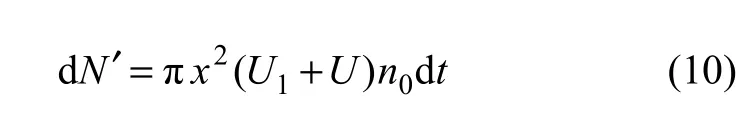
式中:x为电浮室的圆柱底面半径,它的内壁边界距粒子的距离不超过 D/2。电浮室与粒子的位置关系如图6所示。
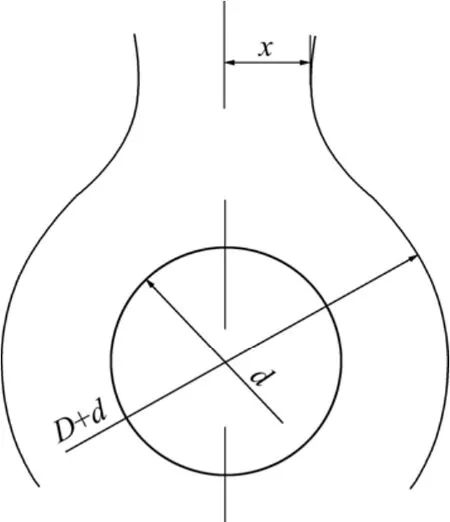
图6 电浮室与粒子的位置关系Fig.6 Positions between electro-flotation room and grain
设电浮室的工作体积为 V,在时间 t内的所有粒子的总碰撞次数为:
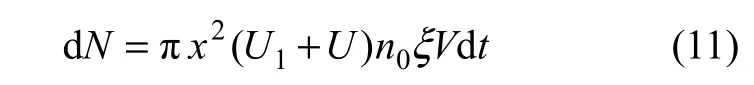
通常,碰撞概率是单位时间内的总碰撞次数与电浮室内粒子总数Vξ之比,因此,
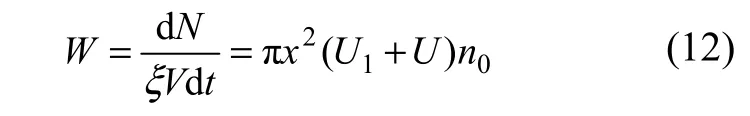
假设在t时间内从电极释放出的平均气泡数为:

式中:ke为该气体的物质的量;AT为电极电流的输出值;It为瞬时电量;ρ为气泡密度。由于输入的电流密度为
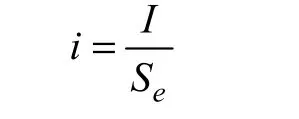
故气泡的平均浓度为:
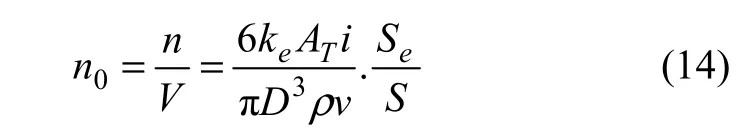
式中:Se为网状电极的工作表面积;S为气泡的表面积。因为液流中粒子和气泡的相对速率分别与单一气泡的上升速率和粒子的下沉速率相对应,因此,为了计算粒子和气泡碰撞的有效截面,可以采用在层流时液流绕过球形阻碍物时的已知函数表达式,即气泡不使液流发生扰动而是绕过粒子,则有:

若将碰撞概率表示成与电流密度的关系,则可以用下式进行描述:
从式(17)中可以看出:当βi取一定数值即电流密度取一定数值时,W(i)有最大值。由此可以推断:在电浮选过程中,随着电流密度的增加,气泡直径减小,粒子和气泡碰撞概率增大,当电流密度达到某一数值时,粒子和气泡碰撞概率达到最大,此后再增加电流密度,气泡直径开始增加,粒子和气泡碰撞概率也相应地有所减小。
4 结论
(1) 基于液体分散相的物理特性,建立了电浮选过程中的液体分散相速率与气泡几何尺寸的数学关系式。
(2) 在酸性介质中,电极材料对所产生的氢气泡直径有明显的影响,气泡平均直径的偏差值为 20~70 μm,在中性介质和碱性介质中电极材料对气泡直径的影响较小,大部分气泡直径分别集中分布在15~25 μm和 15~30 μm。但在整个液流 pH的变化过程中,pH对氧气泡和氢气泡直径均有较大影响。
(3) 电极直径和电流密度在所研究的范围内对氢气泡和氧气泡的影响不大,只是部分气泡直径的分散性明显。随着温度的增加,最大气泡量所对应的氢气泡直径变大,但整个氢气泡的直径分布范围并未发生太大的改变。
(4) 随着电流密度的增加,气泡的直径减小;当电流密度达到某一数值时,粒子和气泡碰撞概率达到最大。
[1] Bhaskar G R, Khangaonkar P R. Electro-flotation of chalcopyrite fines[J]. International Journal of Mineral Processing, 1982, 9(2):133-143.
[2] Murugananthan M, Bhaskar G R, Prabhakar S. Separation of pollutants from tannery effluents by electro-flotation[J].Separation and Purification Technology, 2004, 40(1): 69-75.
[3] Fukui Y, Yuu S. Collection of submicron particles in electro-flotation[J]. Chemical Engineering Science, 1980, 35(5):1097-1105.
[4] 黄光耀, 冯其明, 欧乐明, 等. 利用微泡浮选柱从浮选尾矿中回收微细粒级白钨矿[J]. 中南大学学报: 自然科学版, 2009,40(2): 263-267.
HUANG Guang-yao, FENG Qi-ming, OU Le-ming, et al.Recovery of fine scheelites from flotation tailings by flotation column[J]. Journal of Central South University: Science and Technology, 2009, 40(2): 263-267.
[5] 邓晓刚, 廖振方, 陈德淑. 脉冲电浮水处理过程中的运动学数学模型[J]. 重庆大学学报: 自然科学版, 2008, 31(8):928-931.
DENG Xiao-gang, LIAO Zhen-fang, CHEN De-shu. A kinematic mathematical model of impulse electro-flotation[J].Journal of Chongqing University: Natural Science Edition, 2008,31(8): 928-931.
[6] 邓晓刚, 陈器, 廖振方. 脉冲电浮法在矿物浮选中的应用理论研究[J]. 矿山机械, 2006, 34(4): 66-67.
DENG Xiao-gang, CHEN Qi, LIAO Zhen-fang. Theoretical study to the application of pulse electric flotation method in mineral flotation[J]. Mining & Processing Equipment, 2006,34(4): 66-67.
[7] 梁迎春, 邵会波, 郑传明, 等. 电浮选方法在净化镍离子中的应用研究[J]. 化学通报, 2005, (4): 291-295.
LIANG Ying-chun, SHAO Hui-bo, ZHENG Chuan-ming, et al.Purif ication of Ni2+ions in solution using electroflotation treatment[J]. Chemistry, 2005, (4): 291-295.
[8] 赵健新, 廖振方, 陈德淑. 脉冲电浮水处理池的数学模型与计算方法[J]. 重庆大学学报: 自然科学版, 2005, 28(4): 1-4.
ZHAO Jian-xin, LIAO Zhen-fang, CHEN De-shu. Establishing and application of the mathematical model of the impulse electroflotation reacting tank[J]. Journal of Chongqing University: Natural Science Edition, 2005, 28(4): 1-4.
[9] 林小竹, 谷莹莹, 赵国庆. 煤泥浮选气泡比表面积的计算方法[J]. 煤炭学报, 2007, 32(8): 874-878.
LIN Xiao-zhu, GU Ying-ying, ZHAO Guo-qing. Calculation of the specific surface area of the froth in flotation[J]. Journal of China Coal Society, 2007, 32(8): 874-878.
