桥隧相连结构静动力特性影响因素分析

施成华，雷明锋，彭立敏，赵 丹

(中南大学 土木建筑学院，湖南 长沙，410075)

我国是一个多山国家，受地形条件限制，在铁路线路的某些地段，桥梁与隧道相连，形成桥台伸入隧道内部的复杂结构。正在修建的湖北宜昌至重庆万州铁路出现了多处桥隧相连结构，在宜昌至利川凉雾段桥隧相连隧道还要开行速度为 160 km/h的双层集装箱列车，隧道限界净空高度比以往铁路隧道的高得多，且不同桥隧相连隧道桥台伸入隧道长度不同，如榔坪III号隧道桥台伸入2 m，八字岭与高阳寨隧道桥台伸入长达8 m。近年来，列车荷载作用下隧道结构的振动响应及其对周边环境的影响问题日益受到国内外学者的关注，并采用数值模拟、现场实测等方法对地铁列车振动引起的环境影响问题进行研究[1-5]。在铁路隧道列车振动响应方面主要分析了列车荷载下隧道结构的振动响应规律及其对隧道结构安全性的影响[6-10]，但专门针对桥隧相连结构进行研究的文献很少，文献[11-12]主要分析了列车荷载下桥隧相连结构的动力特性和安全性，对其在列车动载作用下的影响因素没有进行系统分析。在桥台伸入隧道的洞口地段，受桥台及洞口山体的影响，其受力状态极为复杂。铁路桥梁标准设计中虽有桥隧相连结构的设计图纸，但其设计参数没有考虑列车动载的影响。在此，本文作者针对桥隧相连结构静动力特性的影响因素进行研究，这对今后改进和完善桥隧相连结构的设计以及对其进行维修养护等都有一定的指导作用。

1 计算方法与计算模型

1.1 计算方法

动力问题与静力问题的主要区别在于时间变量增加了分析问题的难度，并出现了静力问题中所没有的特殊问题，如特征值分析、阻尼计算等；因此，动力分析主要将无限自由度体系简化为有限自由度体系，将偏微分方程组的求解转换为代数方程组的求解，或者先将偏微分方程组的求解转换为近似的常微分方程组再化为代数方程组，以便数值求解。

结构体系的运动方程为[13]：

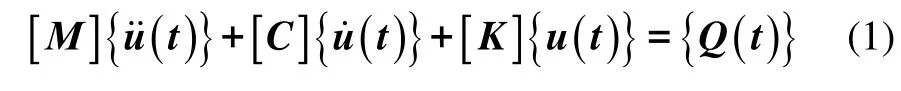
式中：{u(t)}，)}({tu˙和)}({tu˙˙分别为体系的节点位移、速度和加速度向量；[M]和[K]分别为体系的总质量矩阵和总刚度矩阵；[C]为体系总阻尼矩阵，采用瑞利线性组合时，[C]=α[M]+β[K]，α和β为阻尼常数；{Q(t)}为竖向列车振动荷载。

采用摩尔－库仑屈服准则和关联流动法则模拟材料的弹塑性性质；采用无条件稳定的隐式算法即Newmark方法求解运动方程。

1.2 计算模型

采用三维静动力有限元方法进行计算分析。由于动力有限元计算采用时程分析，其荷载步数很多，若采用常规有限元模型(计算范围为隧道跨度的6~10倍)进行计算，一般微型计算机的计算速度和计算容量都难以满足要求。为了解决这个问题，本文采用简化模型并附加质量的方法进行处理，即实际计算中缩小计算范围，增大围岩的密度，保证2种模型的质量相同、边界条件相同，在计算模型的边界处约束其水平位移、与隧道洞内衬砌连接位置的纵向位移以及底部的竖向位移。由于在动力方程中其质量矩阵与刚度矩阵相同，因此，其静动力特性相同。

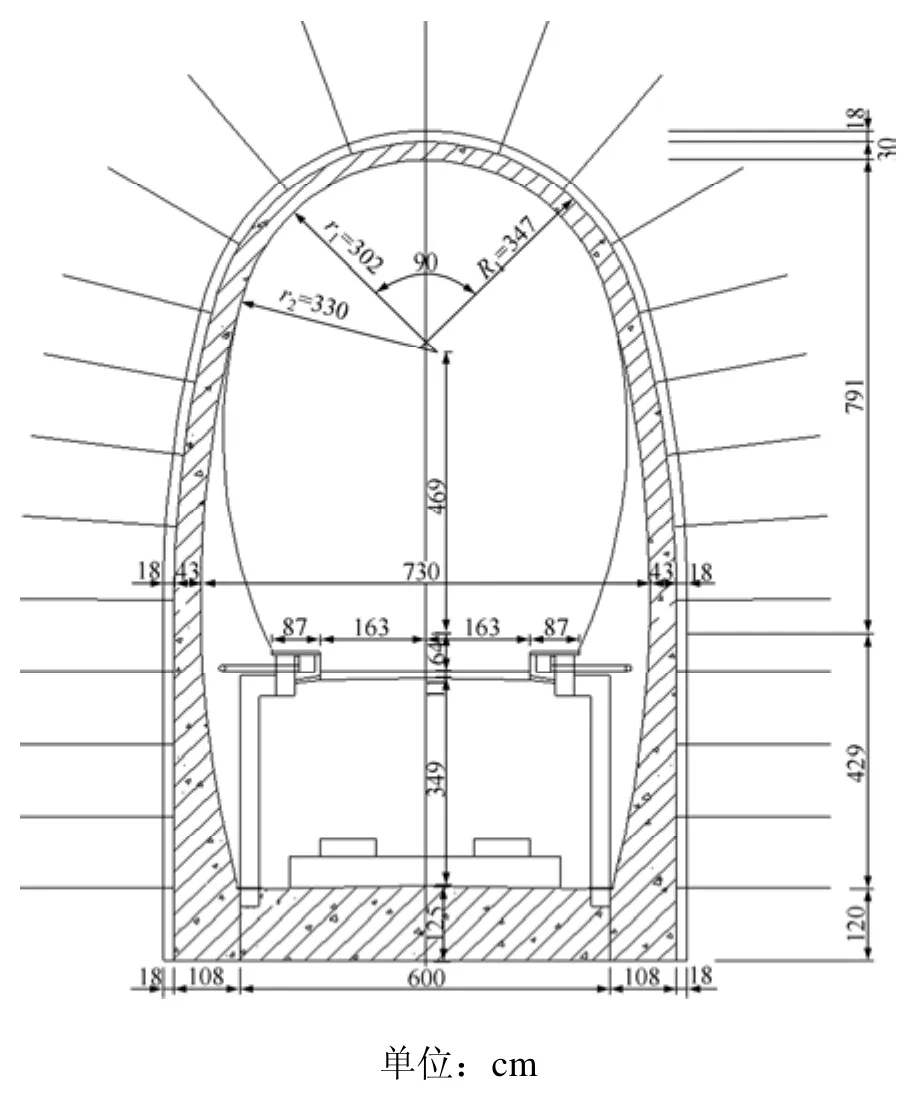
图1 单线桥隧相连结构图Fig.1 Brige-tunnel structure with single line

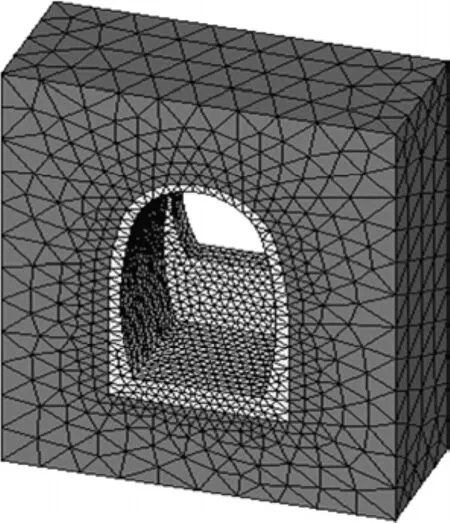
图2 简化计算模型Fig.2 Simplified calculation model

图1 所示为宜万铁路典型单线桥隧相连工点设计图，其简化计算模型如图2所示，隧道四周围岩计算范围各取为隧道洞跨的1倍。为验证简化模型的计算精度，针对单线桥隧相连工况，采用常规模型和简化模型对静动力进行对比计算，列车静载作用下的受力比较如表1所示。其中：σlmax为最大拉应力；σamax为最大压应力；uz为竖向最大变形。列车动载作用下洞口位置横断面的前2阶自振振形见图3和图4。

从表1可以看出：在列车静载作用下2种计算模型，各项力学指标相差均很小；从图3和4可见：简化模型与常规模型的振动特性一致，因此，对于桥隧相连结构采用简化模型进行静动力分析是可行的。以下的动静力计算均是采用简化模型进行的，其具体计算模型见图2(针对不同计算工况其隧道断面和纵向计算长度不同)。

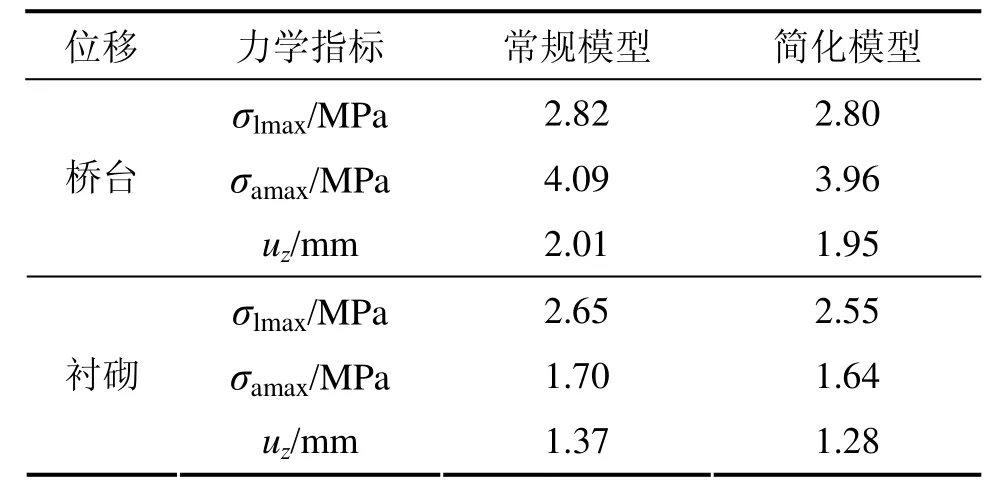
表1 2种计算模型在列车静载下的受力情况比较Table1 Comparison of two models under static train load

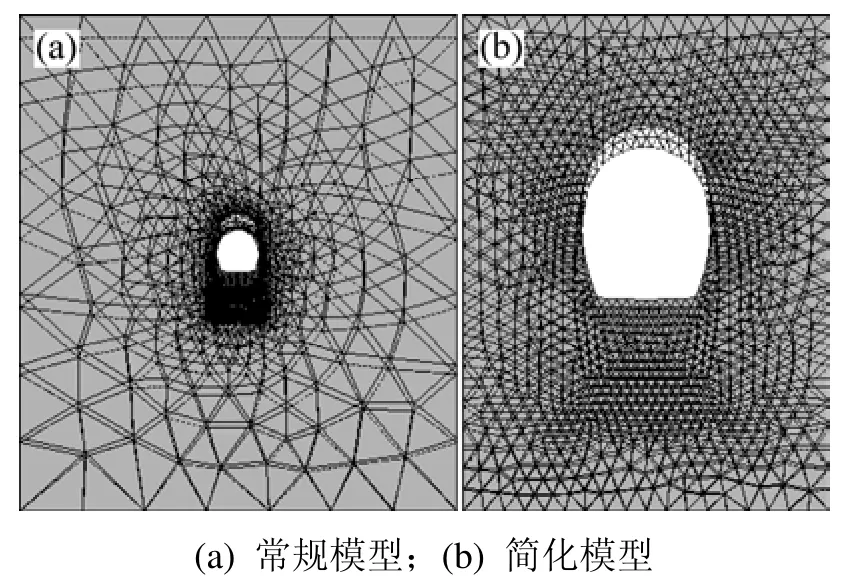
图3 2种计算模型的第1阶振形Fig.3 The first vibration shapes of two models

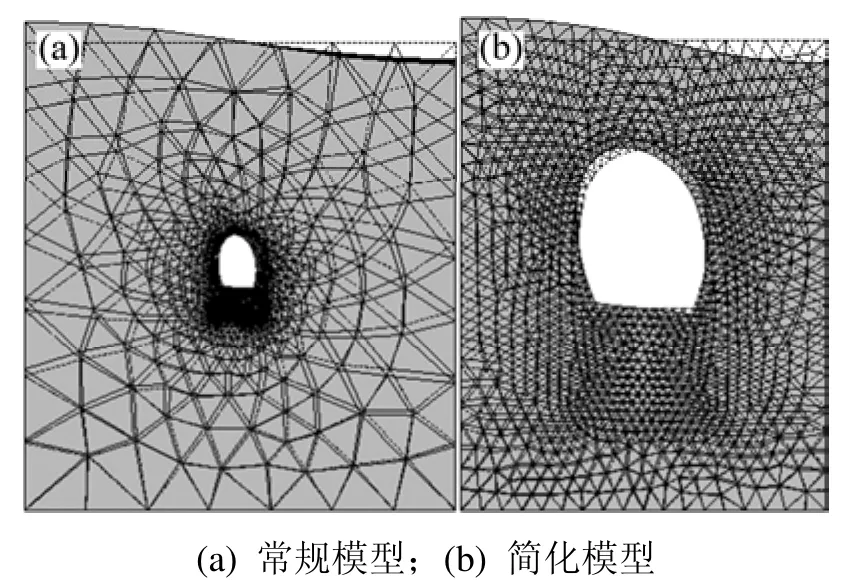
图4 2种计算模型的第2阶振形Fig.4 The second vibration shapes of two models

2 计算荷载与计算参数

2.1 计算荷载

(1) 围岩压力。由于桥隧相连结构只在隧道的洞口段，一般不存在构造应力，因此，计算中围岩压力只考虑自重应力的作用。

(2) 桥梁及列车静载。桥梁荷载取标准设计32 m普通高度后张法预应力混凝土梁[专桥(01)2051]荷载[14]。列车活载采用中-活载布置。因为是双层集装箱，机车轴质量选用目前最大轴质量25 t。桥梁恒、活载加载于桥台模型相应节点处。

(3) 列车制动力。按照桥规规定，制动力荷载按列车静载10%获取，加载于桥台背上。

(4) 列车动载。根据国内外有关列车桥梁振动研究成果建立列车荷载的时间历程函数，并作为外加荷载输入模型计算。计算选用列车轴重动荷载随时间的变化公式为[15]：

式中：F(t)为列车振动荷载；A0为车轮静载；Ai为对应某一频率的振动荷载幅值。当列车速度v已知，量测钢轨基本振动波长Li及相应振幅ai，即可求得振动频率 ωi=2πv/Li及相应的振动荷载幅值(其中，M0为簧下质量)。阻尼选用Rayleigh阻尼，阻尼系数为 α=0.03，β=0.01。

列车轴质量为 25 t，取 A0=250 kN，簧下质量M0=3.5 t，根据文献[4]取L1=10 m，a1=5 mm，L2=2 m，a1=0.6 mm，L3=0.5 m，a1=0.1 mm，可得到对应于v=120 km/h和v=160 km/h的动载表达式。

2.2 计算参数

计算中选取IV级围岩，衬砌及桥台下部选用C30钢筋混凝土，桥台后背挡墙为C30混凝土，具体参数见表2。

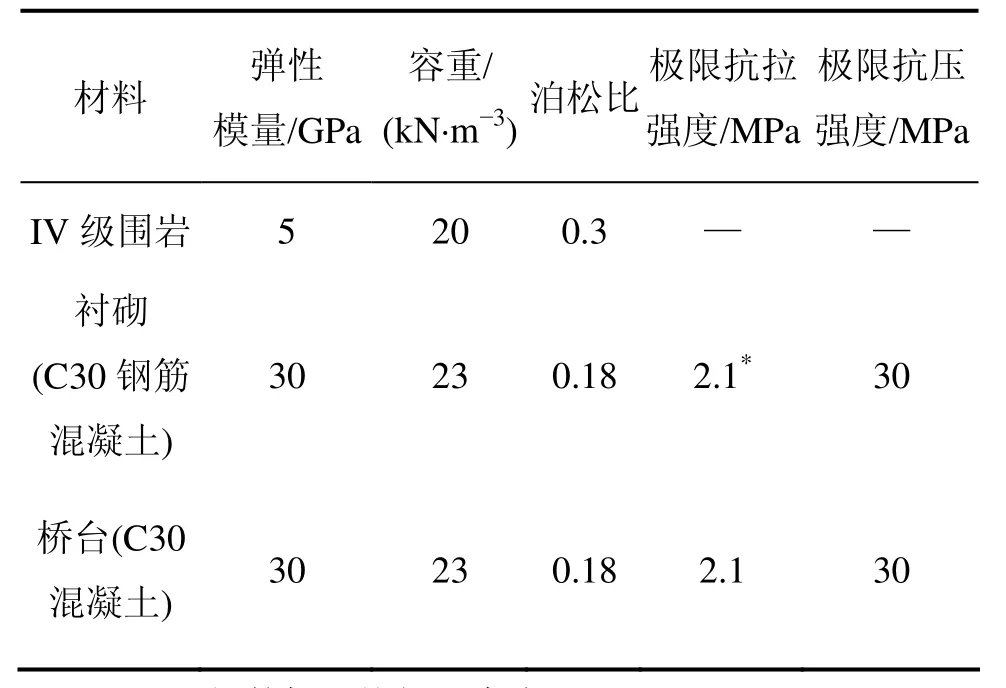
表2 围岩及结构物理力学参数表Table2 Mechanical parameters of structure and surrounding rock

3 桥隧相连结构受力特征影响因素

桥隧相连结构静动力特性的影响因素很多，在列车方面有列车车速和制动力，在隧道设计方面有隧道的高跨比和桥台伸入隧道的长度；此外，还有隧道的埋深和所处的地质条件等。本文仅对列车因素和隧道设计因素进行分析。

3.1 列车车速

在单线及双线工况下，桥隧相连结构承受静载以及时速120和160 km/h列车动载3种不同荷载情况下的受力及变形情况比较如表3和表4所示。

从表3和4可看出：

(1)与静载作用下各项指标相比，列车动载作用下各项指标均增加；时速为120 km/h的列车的动载比静载平均增加7%左右；时速为160 km/h列车的动载比时速为120 km/h列车的动载增加3%左右。

(2) 当车速从120 km/h增加到160 km/h时，位移响应、应力都逐渐增大，但增加幅度较小，振动响应并没有发生质的变化。这是由于激振力与车速和线路不平顺波长有关；在不平顺波长一定的情况下，激振力由列车运行速度决定。车速越快，圆频率ωi越大，振动荷载 Pi也越大。当 ωi过大时，尽管Pi增大，但是结构还来不及产生响应，列车激振荷载已经通过，此时，响应不一定增大。

由于双线结构跨度、线路荷载比单线大，双线结构在静载下的受力以及动载下的各项振动响应指标均比单线结构的大。其中，竖向最大变形增加幅度超过30%，其余在10%左右。

3.2 隧道高跨比

图5和图6所示为单、双线桥隧相连结构(高跨比分别为1.63和1.17)在时速为160 km/h列车动载作用下的围岩塑性区分布情况。可见：单线桥隧相连工况围岩塑性区出现在桥台两侧，而双线工况塑性区出现在隧道拱腰位置，塑性区范围也较单线工况有一定扩大。总体来说，对于高跨比较大的桥隧相连结构，隧道围岩的薄弱区域在隧道的两侧，在施工中应予以加强。

表3 单线工况不同车速下结构受力比较Table3 Structure force under different speed of single line

表4 双线工况不同车速下结构受力比较Table4 Structure force under different speeds of two lines

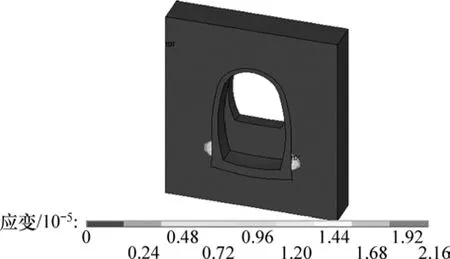
图5 160 km/h列车动载作用下单线工况塑性区分布Fig.5 Distribution of plastic zone of single-line at train speed of 160 km/h

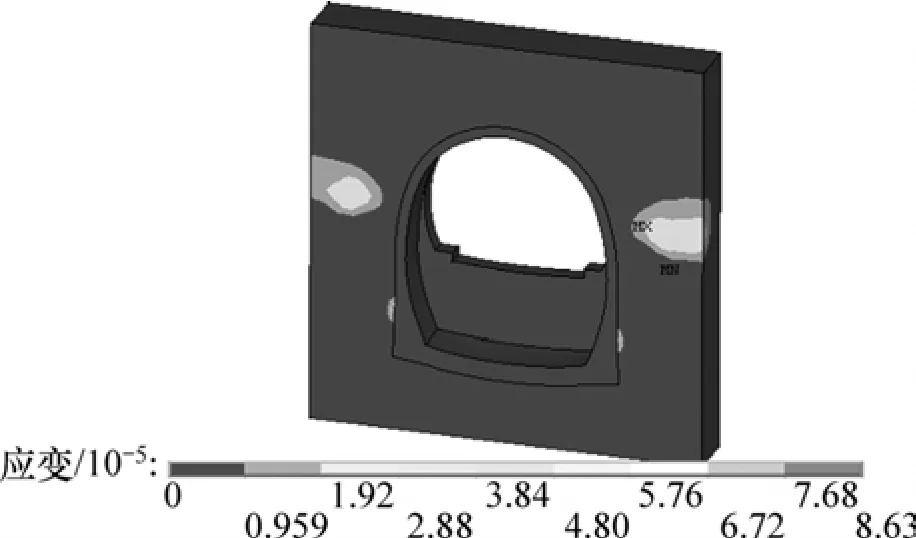
图6 160 km/h列车动载作用下双线工况塑性区分布Fig.6 Distribution of plastic zone of two-lines at train speed of 160 km/h

3.3 列车制动力

为了解列车在桥隧相连段紧急制动时隧道结构受力状态，针对双线桥隧相连工况，分别对列车静载和列车静载加制动力荷载作用下隧道结构的受力状态进行计算，计算结果见表5。从表5可看出：列车制动力对隧道衬砌结构的受力没有影响，只对桥台背部的受力状态有一定影响，但影响程度很小，不需要对整个结构进行额外加强。

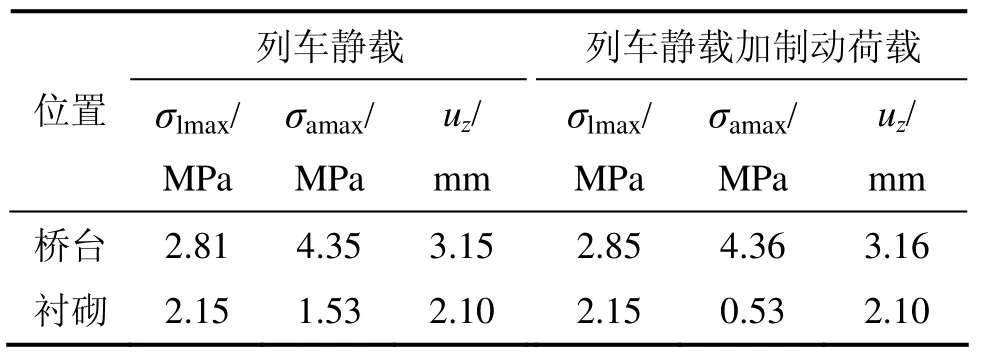
表5 双线工况列车静载和制动力作用下结构受力比较Table5 Structure force under static load and braking force of two-lines

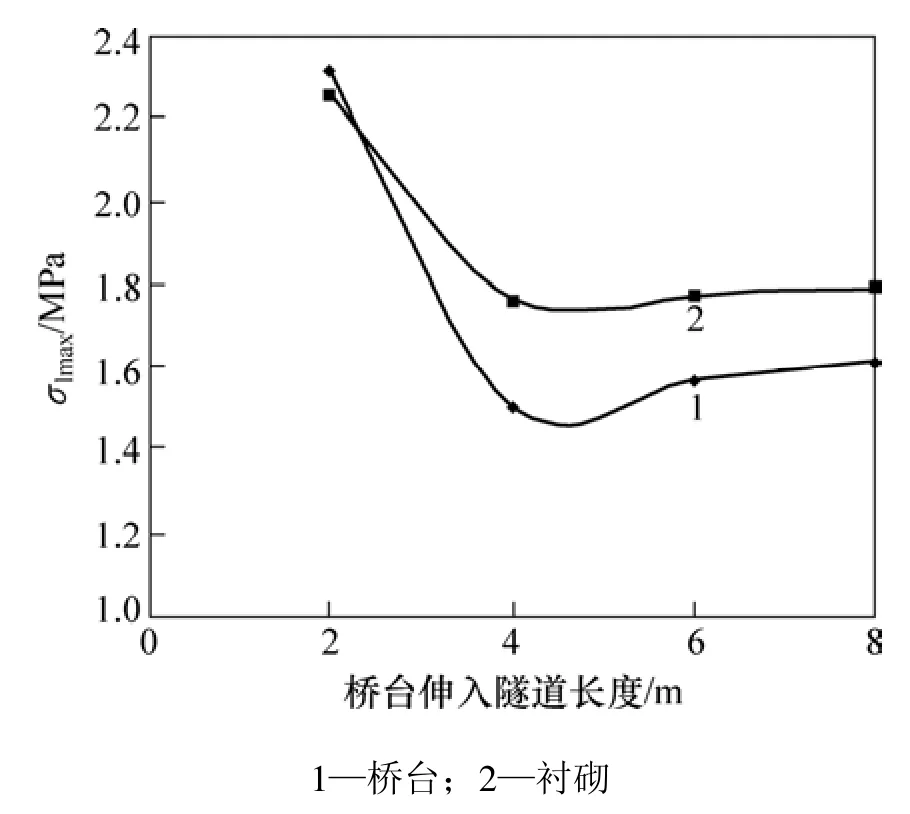
图7 静载作用下桥台衬砌最大拉应力Fig.7 Greatest tensile stress of abutment lining under static load

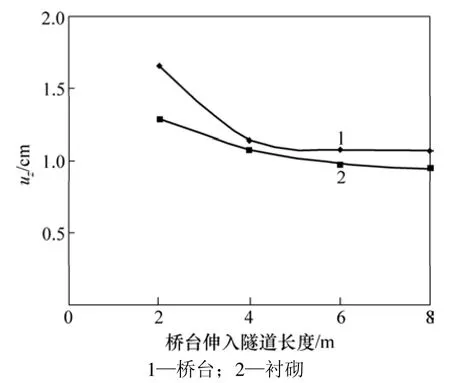
图8 静载作用下桥台衬砌竖向最大变形Fig.8 Greatest compressive stress of abutment lining under static load

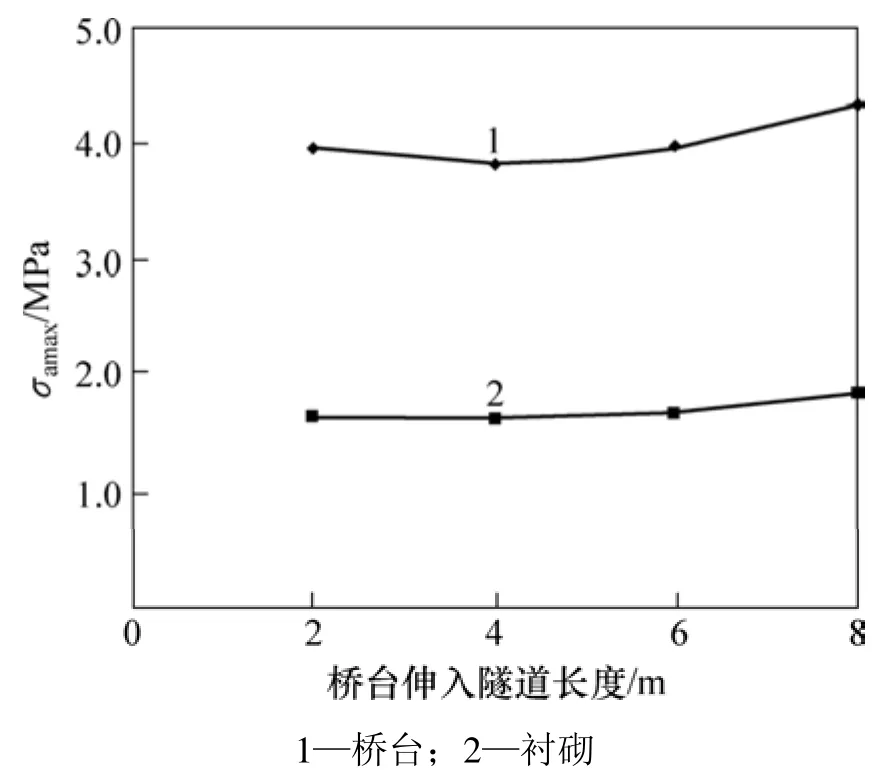
图9 静载作用下桥台衬砌最大压应力Fig.9 Greatest vertical deformation of abutment lining under static load

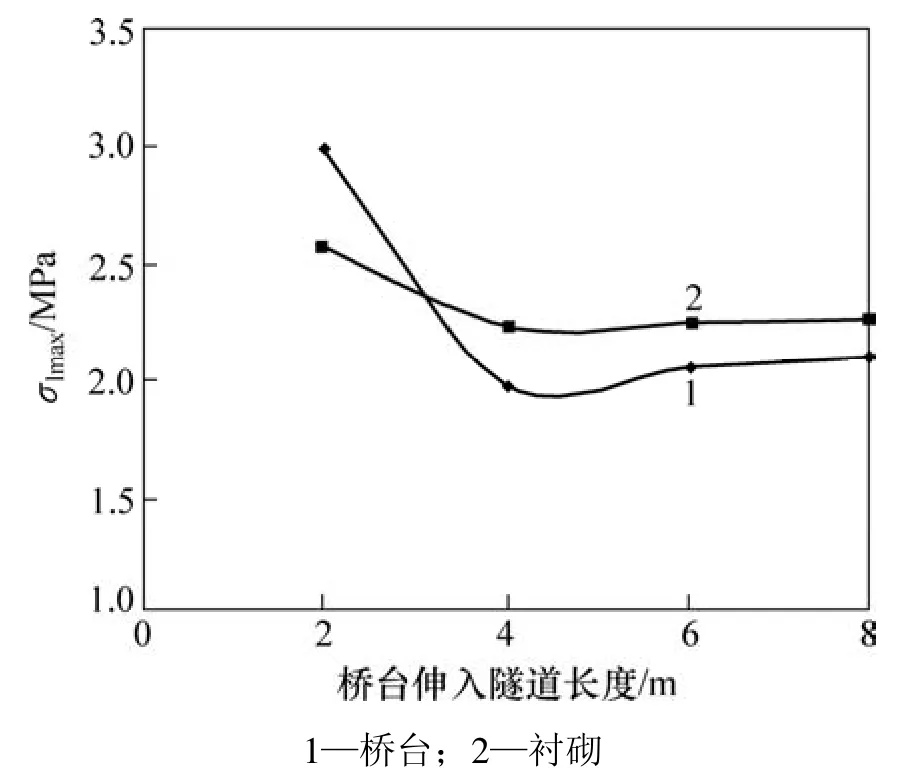
图10 160 km/h车速的动载下桥台衬砌最大拉应力Fig.10 Greatest tensile stress of abutment lining at train speed of 160 km/h

3.4 桥台伸入隧道长度

为比较桥台伸入隧道不同长度时桥隧相连结构受力状态的变化，针对单线桥隧相连结构，分别对桥台伸入隧道长度分别为2，4，6和8 m 4种情况进行静、动载计算。在列车静载作用下结构受力的情况如图7~9所示，时速160 km/h动载作用下结构受力情况如图10~12所示。

从图 7~12可看出：随着桥台伸入隧道长度的增加，桥台和衬砌的最大压应力变化不明显，但竖向最大变形和最大拉应力明显减小，围岩屈服范围也明显减小，并且从2 m到4 m变化明显，而4 m以后变化很小。由此可知：在列车静动载作用下，随着桥台伸入隧道长度的增加，桥隧相连结构受力更加合理；但伸入长度超过4 m后，受力状态趋于平稳。因此，从受力状态分析，桥台应至少伸入隧道4 m。

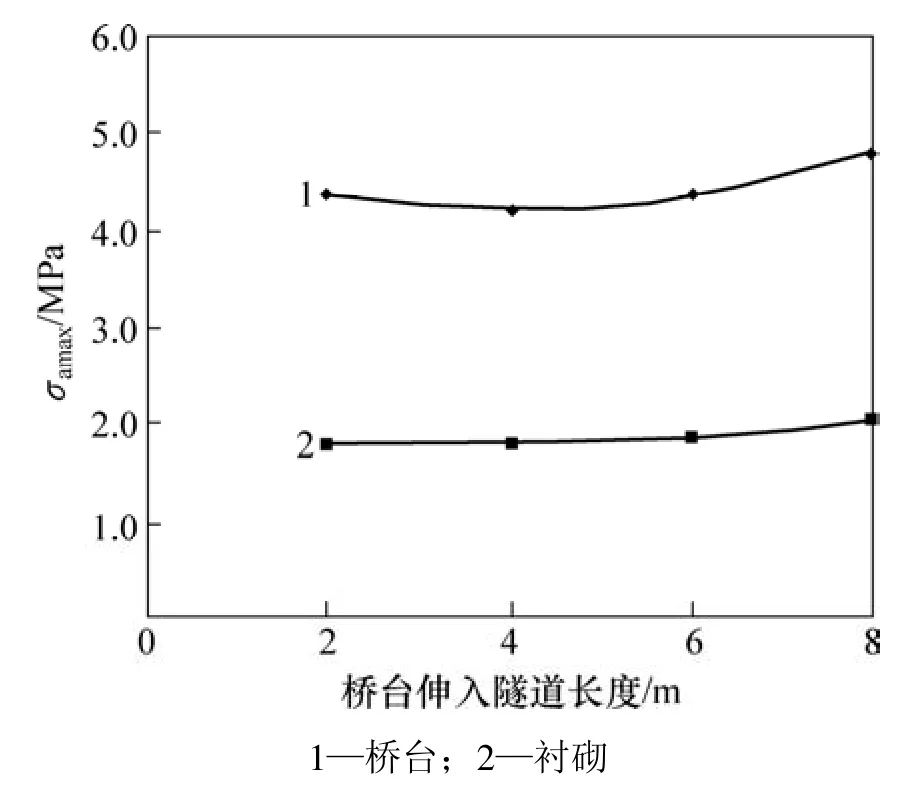
图11 160 km/h车速的动载下桥台衬砌最大压应力比较Fig.11 Greatest compressive stress of abutment lining at train speed of 160 km/h

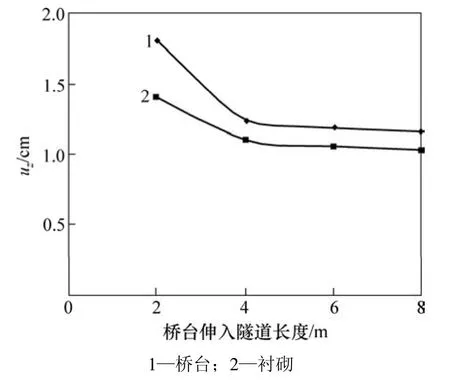
图12 160 km/h车速的动载下桥台衬砌竖向最大变形Fig.12 Greatest vertical deformation of abutment lining at train speed of 160 km/h

4 结论

(1) 列车动载对桥隧相连结构的受力状态有一定影响，且随着行车速度的增大，影响程度增加，但增加的幅度不大，其中，120 km/h列车动载作用下结构各项指标比静载平均增加7%，160 km/h列车动载又比120 km/h列车动载增加3%左右。

(2) 双线结构在几种静动力荷载作用下各项指标均比单线结构大，其中，竖向最大变形增加幅度超过30%，其余在10%左右。

(3) 桥隧相连结构在承受制动力荷载时，各项力学指标与列车静载作用下的指标接近，说明制动力对桥隧相连段结构影响较小。

(4) 对于单线桥隧相连结构，在列车静载或制动力、动力荷载作用下，随着桥台伸入隧道长度的增加，桥隧相连段结构受力更加合理。但长度超过4 m后，受力状态基本趋于平稳。因此，从受力状态分析，桥台应伸入隧道长度至少为4 m。

[1] Hunt H E M. Modelling of rail vehicles and track for calculation of ground-vibration transmission into buildings[J]. Journal of Sound and Vibration, 1996, 193(1): 185-194.

[2] Forrest J A, Hunt H E M. A three-dimensional tunnel model for calculation of train-induced ground vibration[J]. Journal of Sound and Vibration, 2006, 294(4): 678-705.

[3] 刘维宁, 夏禾, 郭文军. 地铁列车振动的环境响应[J]. 岩石力学与工程学报, 1996, 15(增刊): 586-593.

LIU Wei-ning, XIA He, GUO Wen-jun. Study of vibration effects of underground trains on surrounding environments[J].Chinese Journal of Rock Mechanics and Engineering, 1996,15(Suppl): 586-593.

[4] 张玉娥, 白宝鸿. 地铁区间隧道列车振动响应测试与数值分析[J]. 石家庄铁道学院学报, 1993, 6(2): 7-14.

ZHANG Yu-e, BAI Bao-hong. The vibration test and numerical analysis of underground trains[J]. Journal Shijiazhuang Railway Institute, 1993, 6(2): 7-14.

[5] 潘昌实, 谢正光. 地铁区间隧道列车振动测试与分析[J]. 土木工程学报, 1990, 23(2): 21-28.

PAN Chang-shi, XIE Zheng-guang. The test and analysis on vibration of underground train[J]. China Civil Engineering Journal, 1990, 23(2): 21-28.

[6] Lombaert G. The validation of a numerical prediction model for train traffic induced vibrations by in situ experiments[C]//Proceedings of the 25th International Conference on Noise and Vibration Engineering. Leuven, 2000: 379-386.

[7] Degrande G, Othman R, Othman R, et al. A numerical model for ground-borne vibrations from underground railway traffic based on a periodic finite element boundary element formulation[J].Journal of Sound and Vibration, 2006, 293(3/5): 645-666.

[8] 黄娟, 彭立敏, 陈松洁. 高速移动荷载作用下铁路隧道的动力响应分析[J]. 郑州大学学报: 工学版, 2008, 29(3): 117-121.

HUANG Juan, PENG Li-min, CHEN Song-jie. Dynamic responses of railway tunnels under high-speed moving Loads[J].Journal of Zhengzhou University: Engineering Science, 2008,29(3): 117-121.

[9] Chai J F, Teng T J. Identification of source time function for train-induced vibration of underground tunnels[C]//17th World Conference on Non-Destructive Testing. Shanghai, 2008: 9-16.

[10] 王志勇, 梁波. 高速列车荷载作用下仰拱对隧道整体动力特性的影响分析[J]. 现代隧道技术, 2008, 45(5): 28-33.

WANG Zhi-yong, LIANG Bo. Effect of invert arch on the integral dynamic characteristics of a tunnel under high-speed train loading[J]. Modern Tunneling Technology, 2008, 45(5):28-33.

[11] 李耀珠. 桥隧相连地段隧道衬砌动力特性研究[D]. 长沙: 中南大学土木建筑学院, 2005: 8-25.

LI Yao-zhu. Study on the static and dynamical characteristic of tunnel -bridge structure[D]. Changsha: Central South University.School of Civil Engineering and Architecture, 2005: 8-25.

[12] SHI Cheng-hua, PENG Li-min, LEI Ming-feng. Safety analysis of bridge-tunnel structure under train load action[J]. Progress in Safety Science and Technology, 2006, 6(10): 2192-2195.

[13] 张汝清, 殷学纲, 董明. 计算结构动力学[M]. 重庆: 重庆大学出版社, 1987: 10-30.

ZHANG Ru-qing, YIN Xue-gang, DONG Ming. Calculating dynamics of structure[M]. Chongqing: Chongqing University Press, 1987: 10-30.

[14] 铁道部专业设计院. 铁路工程设计技术手册——混凝土桥[M]. 北京: 中国铁道出版社, 1999: 10-25.

Specialized Design Institute of Railway Department. Design manual of railway engineering: Concret bridge[M]. Beijing:China Railway Publishing House, 1999: 10-25.

[15] 李德武. 列车振动荷载的数定分析[J]. 甘肃科学学报, 1998,10(2): 25-29.

LI De-wu. A deterministican analysis of dynamic train loading[J].Journal of Gansu Sciences, 1998, 10(2): 25-29.