复小波变换-自适应滤波算法抑制局部放电窄带干扰
2011-06-01丁家峰何腾波
盛 驰,曹 建,丁家峰,何腾波
(中南大学 物理科学与技术学院,湖南长沙,410083)
来自广播、通信、谐波等的周期性窄带干扰是变压器内局部放电(PD)检测中主要的干扰成分之一,其能量比PD信号大,往往能将检测到的PD信号湮没,因此,必须加以抑制。常用的方法有二阶级联IIR格型陷波滤波算法[1]、小波包熵阈值法[2]、小波变换阈值法[3]、自适应滤波算法[4]。其中,自适应滤波算法无需预先知道干扰频率信息,能取得较好的滤波性能。但是,自适应滤波算法只对单一频率或少量不同频率的窄带干扰有较好的滤波性能,而局部放电在线监测中往往存在多种频率的窄带干扰,且频率范围差别较大,滤波器权系数难以收敛到最佳值。而且在低信噪比情况下,自适应算法性能也大大降低。在干扰频率多且与PD信号频谱重叠严重以及信噪比较低的情况下,上述各种窄带抑制方法都不理想。可见,干扰频率多和信噪比低是窄带抑制中的难题。近年来,复小波变换的研究发展为抑制窄带干扰提供了新的方法。复小波分解能生成实部和虚部 2个正交方向上的小波系数,均具有小波变换的分频特性,经滤波及复小波重构后,可得到实部和虚部2个简单信息,然后,可根据文献[5-8]提出的复合信息算法,利用简单信息构造复合信息,以增加复小波变换处理信号的手段和性能。在此,本文作者提出一种基于复小波变换的自适应滤波与复合信息技术来抑制窄带干扰的新算法。该算法在存在多种干扰频率以及信噪比很小的情况下依然能取得非常好的滤波效果。
1 复小波变换
1.1 复小波的构造
文献[5-6]指出,只要采用保持实小波滤波器的幅频特性、改变其相频特性的方法,就能获得与现有实小波相同特性(正交、紧支撑、消失矩和正则性等)的复小波。文献[9]给出了由上述方法构造出的db4小波,本文采用该复小波对PD信号进行去噪。
1.2 复小波变换的分频特性
复小波与实小波具有相同特性,且进行小波变换的算法完全一致,因此,复小波变换应具有与实小波变换相同的特性。文献[10]指出:PD信号经复小波变换后系数的实部与虚部分别与由复小波各自形成的单一实小波变换后的系数的实部和虚部基本一致。
实小波变换具有一大特点就是其分频特性。在实小波变换中,由{h0,k}(低通滤波器)和{h1k}(高通滤波器)组成的多采样滤波器组对原始信号进行频域二尺度划分。把原始信号占据的总频带(0~fs/2)定义为空间V0,经第1级分解后,V0被划分为低频的V1(频带为0~fs/4)和高频的W1(频带为fs/4~f/2) 2个子空间;经第2级分解后,V1又被划分为低频的 V2(频带为 0~fs/8)和高频的W2(频带为fs/8~fs/4) 2个子空间。
因此,复小波变换也具有这种分频特性,第j层复小波系数的实部和虚部均包含了原始信号在频带fs/2j+1~fs/2j内的分量。
1.3 复小波的一种新复合信息
文献[5]指出:通过复小波变换,能够得到实部Iwr和虚部Iti2种基本信息,并容易得到模信息Im和相角信息Itp,把这4种信息定义为简单信息。以上简单信息可以构造下列复合信息:实部与相角乘积Irp、虚部与相角乘积Iip、模与相角乘积Imp、实部、虚部的绝对值与相角乘积 Itrip以及实部虚部组合的复合信息序列。
文献[6,11]通过对各种信息提取信号能力的比较发现,实部信息Ir对信号相位、极性的提取能力以及信号波形的保持能力较强,但是,对噪声的抑制能力较弱;而模信息Im对信号的能量有很强的集聚作用,能有效抑制噪声,提高信噪比。因此,笔者构造一种新的复小波变换实部与模平方乘积的复合信息 Irm2,即:
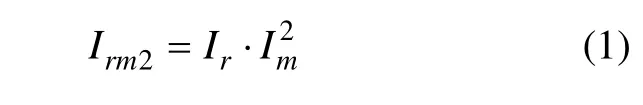
该复合信息不仅能有效提高信噪比,同时也能减小波形畸变。
2 复小波变换-自适应滤波算法
2.1 LMS自适应滤波算法
自适应滤波算法的研究已经非常广泛和深入,其中用于消除窄带干扰的基于 LMS算法的横向滤波器系统框图如图1所示。
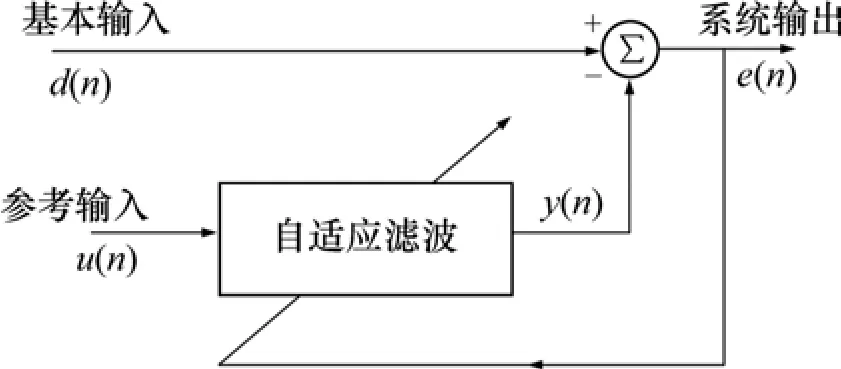
图1 自适应滤波器框图Fig.1 Diagram of adaptive filter
基本输入由信号和窄带干扰组成,而参考输入为与基本输入中的窄带干扰同频率的窄带信号,从基本输入中减去自适应滤波输出,即可消除窄带干扰[12]。
自适应滤波器的性能主要受滤波器的阶数以及收敛因子µ的影响,其中µ最关键,其将影响收敛速度、稳定性及收敛解的准确性:µ过大易造成系统发散,稳态误差也较大;µ过小则收敛速度慢,收敛过程产生的杂波较大,要同时增加滤波器阶数才能达到适当收敛,这样,就增加了计算量。
2.2 复小波变换逐层自适应滤波
上述自适应滤波算法对于单一频率或少量不同频率的窄带干扰,可以通过大量仿真的方法获得最优的µ,但是,当信号中同时出现多种干扰频率,且干扰频率范围较宽时,就很难通过设置µ来获得理想的滤波效果[13]。为克服这一弱点,可利用复小波变换的分频特性先将信号分解到不同的频段上,然后,对各频段的信号逐层进行自适应滤波。由于窄带干扰也随信号被分解到各频段内,每个频段内不同频率的窄带干扰较少且频率相差较小,更容易获得最佳的µ以获得更好的滤波性能。
以往用于抑制窄带干扰的自适应滤波的参考输入是通过对基本输入的延时来获得的。通过实验发现:若输入的延时太小,则不能去除PD信号相关性,对滤波性能也会有负面影响,若输入的延时较大,则对采样点较少的信号造成较大的信息损失。而同一层复小波系数的实部和虚部均包含同一频段内相同的窄带干扰,且两者PD信号分量的相关性很弱,因此,用实部和虚部分别作为基本输入和参考输入可避免延时单元的使用,从而获得更好的滤波性能。
复小波变换自适应滤波算法如图2所示,其步骤如下:
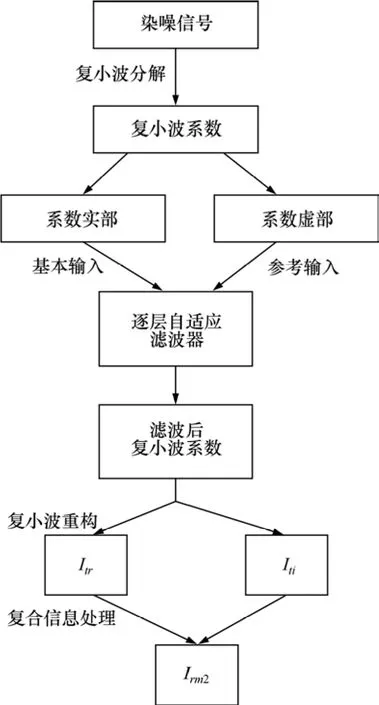
图2 复小波变换逐层自适应滤波流程Fig.2 Level-by-level adaptive filtering based on complex wavelet transform
(1) 对染噪信号进行复小波变换,得到一组复小波系数。
(2) 以复小波系数的实部和虚部分别作为基本输入和参考输入进行逐层自适应滤波处理。
(3) 对逐层自适应滤波后得到的小波系数进行重构,得到基本信息Ir和Ii。
(4) 对基本信息 Ir和 Ii进行复合信息处理,得到复合信息Im2即最终去噪结果。
2.3 逐层自适应滤波器参数设置
逐层自适应滤波框图见图 3。复小波分解后的小波系数在低尺度上点数较多,波形较密集;而高尺度上点数少,波形较迟缓。因此,各层次上的自适应滤波器阶数应该随尺度变化而不是全局的,否则,若阶数设置过低,则对低尺度上的系数根本达不到滤波效果,若过高,则会使高尺度上系数的能量损失过大,造成波形失真。因此,提出下面的逐层滤波器阶数设置方法:

式中:M(i)为第 i层滤波器的阶数,M0为初始值,λ为步进值。
自适应滤波器的收敛因子µ可取一全局量。

图3 逐层自适应滤波器框图Fig.3 Diagram of level-by-level adaptive filter
3 仿真分析
3.1 局放仿真信号及去噪性能参数
局部放电脉冲可以用以下数学模型来等效[13]:单指数衰减形式(脉冲1)、双指数衰减形式(脉冲2)、单指数衰减振荡形式(脉冲 3)、双指数衰减振荡形式(脉冲4),时间常数τ为1 µs,振荡频率fc为1 MHz,采样频率为10 MHz,采样点数为4 000。7种窄带周期干扰频率分别为100,125,200,250,500 kHz以及1 MHz和2 MHz;幅值相等。原始PD信号与信噪比分别为0 db和-5.26 db的染噪信号如图4所示。
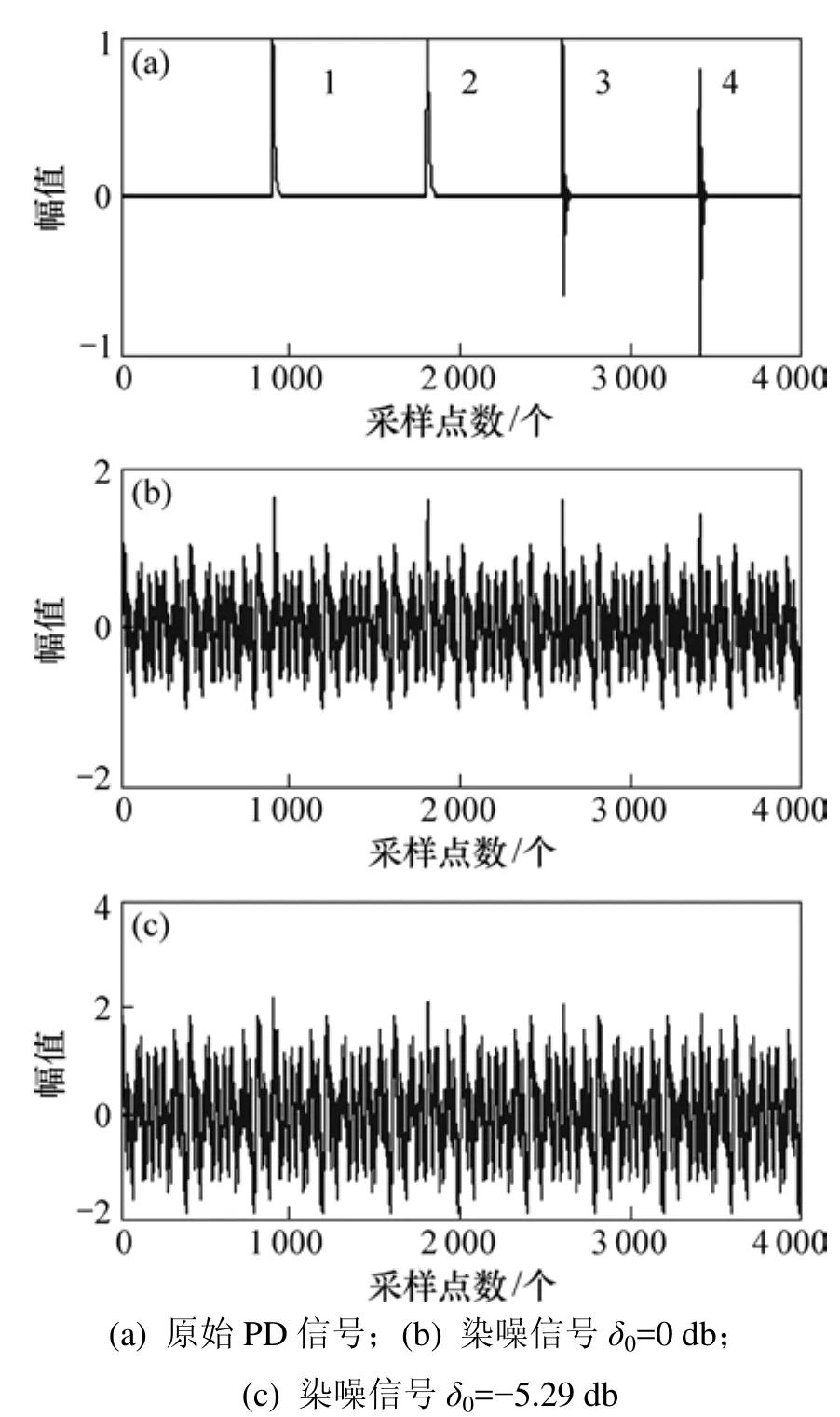
图4 PD仿真信号Fig.4 Emulation of PD signal
去噪性能参数采用去噪前后的信噪比(δ)和波形相似性参数(η)[14-16],其定义分别为:
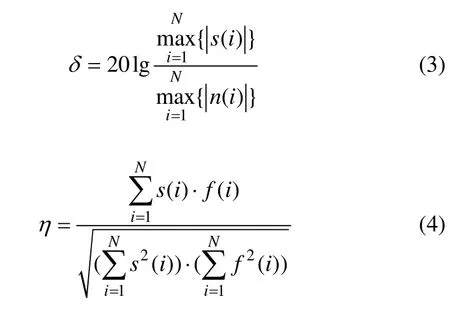
式中:s(i)为原始信号;n(i)为噪声信号;f(i)为去噪后的信号。-1≤η≤1,其中:-1代表变换前后的波形正好反向;0代表两波形正交;1则代表完全相同。
3.2 去噪仿真分析
3.2.1 染噪信号为δ=0 db时的去噪仿真
图5(a)所示为δ0=0 db时的染噪信号经9层db4复小波变换-自适应滤波(CWTAF)后的去噪结果,其中,M0取46,λ取5,全局收敛因子µ取0.13。图5(b)所示为 40阶普通自适应滤波器在不同收敛因子下一组较好的去噪结果;图 5(c)所示为传统小波的去噪结果。普通自适应滤波与传统小波去噪对某些频率下的窄带干扰没有起到抑制作用,且信噪比小,有用信号能量损失大,而复小波变换自适应滤波完全抑制了所有干扰频率,且大大提高了信噪比,性能明显优于前者。
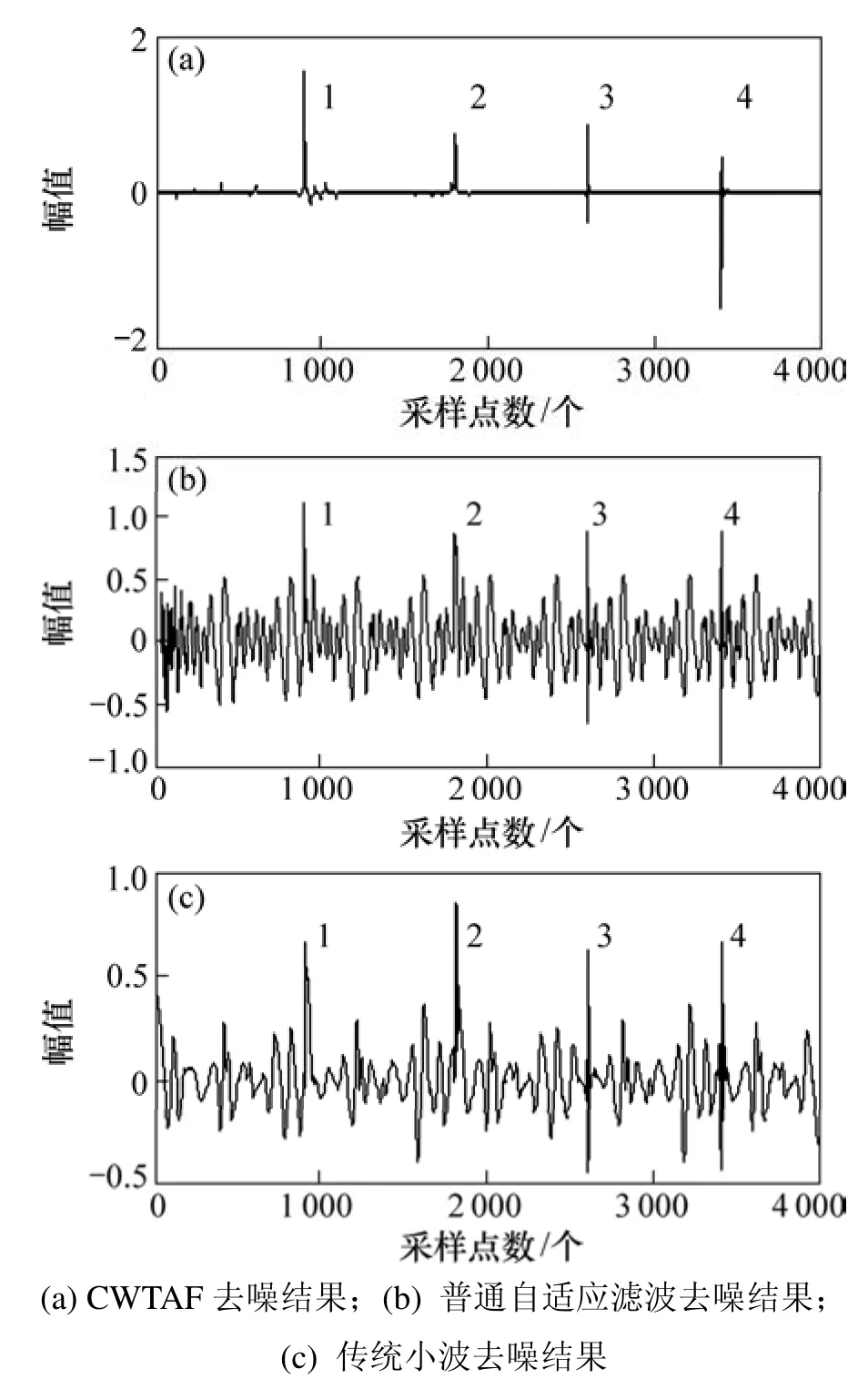
图5 去噪结果Fig.5 Denoising results
表 1~3所示分别为复小波-自适应滤波、普通自适应滤波和传统小波去噪后的δ和η。比较表1~3可以发现:复小波变换-自适应滤波的性能明显更优。复小波变换-自适应滤波后的衰减型脉冲(脉冲1和2)的η明显高于振荡型脉冲(脉冲3和4)的η,尝试采用各种滤波器参数,振荡型脉冲的η也很难有显著提高。
图 6所示为原始信号、加噪信号、复小波变换-自适应滤波和普通自适应滤波后信号的频谱。从图 6可以看到,虽然含有 7种不同的干扰频率,且与 PD信号在低频处重叠严重,复小波变换-自适应滤波将所有7种频率的窄带干扰完全抑制,滤波后频谱与原始信号频谱基本一致,只是振荡型脉冲的振荡频率 1 MHz处衰减稍大。这是因为其与1 MHz的干扰重合,干扰被抑制的同时,信号的能量也被衰减,这也是说振荡型脉冲η较小的原因。而普通自适应滤波无法抑制低频部分几条谱线的干扰,它对5种以上频率的窄带干扰就很难找到合适的参数(如µ、滤波阶数、延迟等)以达到理想的滤波效果。
3.2.2 染噪信号为δ0=-5.29 db时的去噪仿真
在δ0=0 db时,复小波变换-自适应滤波能取得很好的滤波效果,而普通自适应滤波很难抑制低频部分的窄带干扰。这说明对于含有多种干扰频率且与 PD信号在频域重叠严重这一难题,复小波变换-自适应滤波能够很好地解决。
δ0=5.29 db时的去噪情况如图7和表4所示。从图7及表4可以看出:复小波变换-自适应滤波对小信噪比的信号也有很强的提取能力。因此,复小波变换-自适应滤波能同时较好地解决干扰频率多和信噪比低这2个问题。
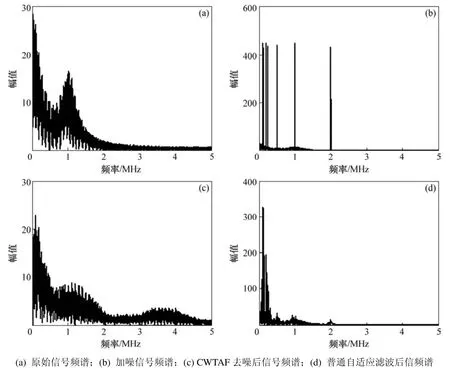
图6 仿真频谱分析Fig.6 Spectrum analysis of simulation
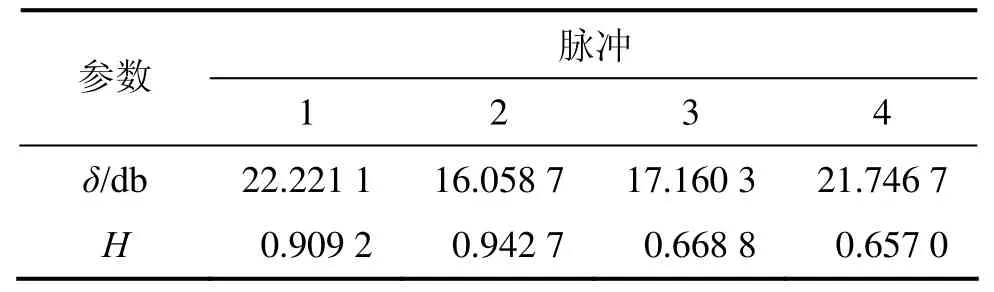
表1 CWTAF去噪后的δ和ηTable1 δ and η of signal denoised by CWTAF
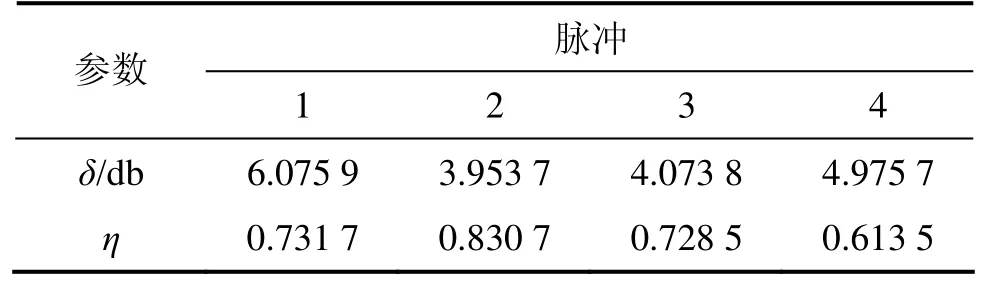
表2 普通自适应滤波去噪后的δ和ηTable2 δ and η of signal denoised by adaptive filter

表3 传统小波去噪后的δ和ηTable3 δ and η of signal denoised by traditional wavelet filter

图7 δ0=-5.29 db时的去噪结果Fig.7 Denoising results when δ0=-5.29 db
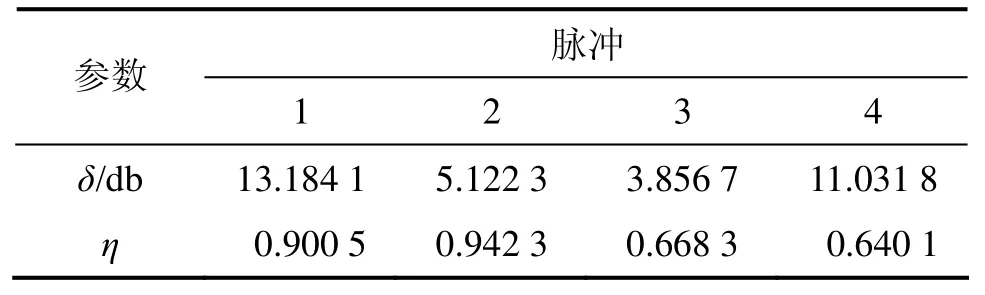
表4 当δ0=-5.29 db时CWTAF去噪后的δ和ηTable4 δ and η of signal denoised by CWTAF when δ0=-5.29 db
4 实测数据去噪结果
为检验本文所提出的复小波变换-自适应滤波去噪能力,笔者从实验室获取了一组沿面放电的PD信号。图8所示为实验室实测信号波形及去噪结果。
由于该数据中还含有白噪声,所以,其窄带抑制效果从时域波形中较难看出。图9所示为对应于图8信号的频谱。从图9可以看出:原始信号中多种不同频率窄带干扰均得到有效抑制。
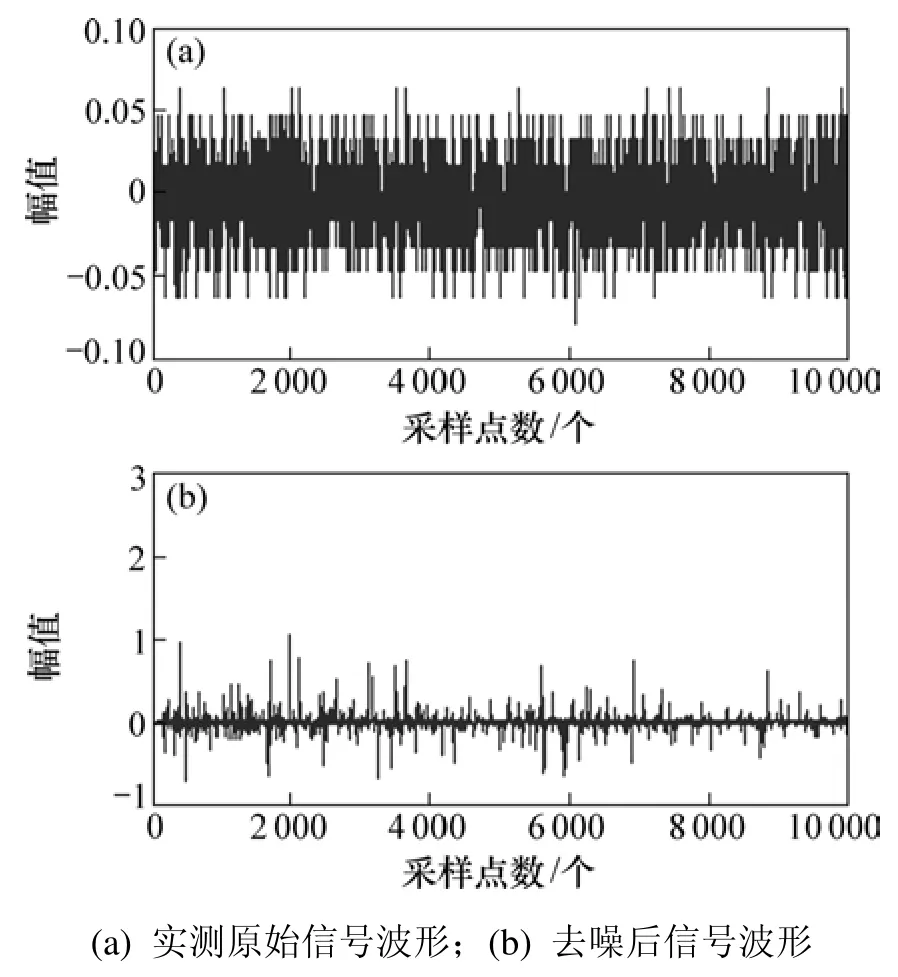
图8 实测PD信号去噪Fig.8 Denoising of lab signals

图9 与图8波形相对应的频谱图Fig.9 Spectrum of signal in Fig.8
5 结论
(1) 复小波变换利用其分频特性将信号分解到不同的频段内,然后对各尺度的复小波系数进行逐层自适应滤波,可以使各个频段内的窄带干扰数少且频率接近,有利于自适应滤波器更好地收敛,从而能很好地解决PD信号窄带干扰频率数多的问题。
(2) 以复小波系数的实部和虚部分别为自适应滤波器的基本输入和参考输入并采用逐层自适应滤波器阶数的设定,能大大提高复小波变换自适应滤波算法的性能。
(3) 采用实部与模平方乘积的复合信息 Irm2能大大提高对低信噪比信号的提取能力以及对信号形状的维持能力,有效地解决了PD信号信噪比低的问题。
[1] 王晓蓉, 杨敏中, 严璋. 电力设备局部放电测量中抗干扰研究的现状和展望[J]. 电网技术, 2000, 24(6): 41-45.
WANG Xiao-rong, YANG Min-zhong, YAN Zhang. Review and prospect of rejecting interference in partial discharge measurement of power equipment[J]. Power System Technology,2000, 24(6): 41-45.
[2] 毕为民, 唐炬, 姚陈果, 等. 基于熵阈值的小波包变换抑制局部放电窄带干扰的研究[J]. 中国电机工程学报, 2003, 23(5):128-131.
BI Wei-min, TANG Ju, YAO Chen-guo, et al. Simulation and experiment study on wavelet packet decomposition based on entropy threshold for DSI rejection of PD[J]. Proceedings of the CSEE, 2003, 23(5): 128-131.
[3] 胡明友, 谢恒堃, 蒋雄伟, 等. 基于小波变换抑制局部放电监测中平稳性干扰的滤波器的研究[J]. 中国电机工程学报,2000, 20(1): 37-40.
HU Ming-you, XIE Heng-kun, JIANG Xiong-wei, et al. Study on WTST-NST filter used for suppression of stationary in PD monitoring[J]. Proceedings of the CSEE, 2000, 20(1): 37-40.
[4] 赵学梅, 王力欣, 蔡惟铮.局部放电在线监测中的自适应滤波方法[J]. 电力系统自动化, 1999, 23(20): 29-32.
ZHAO Xue-mei, WANG Li-xin, CAI Wei-zheng. Adaptive filter method for partial discharge on-line measurement system[J].Automation of Electric Power Systems, 1999, 23(20): 29-32.
[5] 陈祥训. 正交紧支复小波的生成及其在电力系统的应用[J].中国电机工程学报, 2000, 20(7): 83-88.
CHEN Xiang-xun. Complex compactly supported orthonormal wavelets and their applications in power system[J]. Proceeding of the CSEE, 2000, 20(7): 83-88.
[6] 唐炬, 许中荣, 孙才新, 等. 应用复小波变换抑制GIS局部放电信号中白噪声干扰的研究[J]. 中国电机工程学报, 2005,25(16): 30-34.
Tang Ju, Xu Zhong-rong, SUN Cai-xin, et al. Application of complex wavelet transform to suppress white-noise interference in GIS PD signal[J]. Proceedings of the CSEE, 2005, 25(16):30-34.
[7] HE Hai-bo, CHENG Shi-jie, ZHANG You-bing, et al. Analysis of reflection of signal transmitted in low-voltage powerline with complex wavelet[J]. IEEE Trans Power Delivery, 2000, 19(1):86-91.
[8] 唐炬, 邓志勇, 周倩, 等. 一种抑制 PD白噪干扰的有效复合信息技术[J]. 重庆大学学报, 2008, 31(4): 401-407.
TANG Ju, DENG Zhi-yong, ZHOU Qian, et al. An effective technique of combining information for reducing the white noise of partial discharge signals[J]. Journal of Chongqing University,2008, 31(4): 401-407.
[9] 唐炬, 谢颜斌, 朱伟, 等. 用于复小波变换的 EWC阈值法抑制周期性窄带干扰[J]. 电力系统自动化, 2005, 29(7): 43-47.
TANG Ju, XIE Yan-bin, ZHU Wei, et al. Suppression of narrowband interference with EWC threshold method for complex wavelet transform[J]. Automation of Electric Power Systems, 2005, 29(7): 43-47.
[10] 崔雪梅, 孙才新, 李新, 等. 实小波与复小波对局部放电在线监测中提取信号特征的特点研究[J]. 电工技术学报, 2004,19(7): 90-94.
CUI Xue-mei, SUN Cai-xin, LI Xin, et al. Analysis of real wavelet and complex wavelet transform in extracting PD signal feature[J]. Transactions of China Electrotechnical Society, 2004,19(7): 90-94.
[11] 唐铭, 唐炬, 谢颜斌, 等. 一种用于复小波变换的有效系数阈值[J]. 重庆大学学报: 自然科学版, 2006, 29(10): 5-9.
TANG Ming, TANG Ju, XIE Yan-bin, et al. Effective coefficient threshold for complex wavelet transform[J]. Journal of Chongqing University, : Natural Science Edition, 2006, 29(10):5-9.
[12] Hanykin S S. Adaptive filtering theory[M]. 3rd ed. New Jersey:Prentice Hall, 1985: 175-182.
[13] 黄成军, 郁惟镛. 基于小波分解的自适应滤波算法在抑制局部放电窄带周期干扰中的应用[J]. 中国电机工程学报, 2003,23(1): 107-111.
HUANG Cheng-jun, YU Wei-yong. Study of adaptive filter algorithm based on wavelet analysis in suppressing PD’s periodic narrow band with noise[J]. Proceedings of the CSEE,2003, 23(1): 107-111.
[14] Zhou X, Zhou C, Kemp I J. An improved methodology for application of wavelet transform to partial discharge measurement denoising[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2005, 12(3): 586-594.
[15] Werle P, Akbari A, Borsi H, et al. Enhanced online PD evaluation on power transformers using wavelet techniques and frequency rejection filter for noise suppression[C]//IEEE Int Sym Electrical Insulation, Piscataway: IEEE, 2002: 195-198.
[16] 唐炬, 彭莉, 谢颜斌. 一种用于抑制白噪声的分层复阈值算法[J]. 中国电机工程学报, 2007, 27(21): 25-30.
TANG Ju, PENG Li, XIE Yan-bin. An algorithm of complex multilevel threshold for reducing white-noise[J]. Proceedings of the CSEE, 2007, 27(21): 25-30.
