基于GRNN神经网络的中厚板轧机厚度预测

郭 斌，孟令启，杜 勇，马生彪

(郑州大学 机械工程学院，河南 郑州，450001)

中厚板轧件的厚度精度是轧件重要的质量指标之一[1-2]，厚度控制的实质是对轧机辊缝进行控制[3]。传统的厚度预测方法是通过压靠法或者轧制法测得不同轧制力下的轧机弹跳值, 得到轧机机座的实测弹跳曲线，然后，建立机座弹跳曲线的数学模型。由于在数学模型的建立过程中忽略和简化了许多因素，因此，计算的厚度误差较大，不能满足人们日益增长的需要[4-5]。人工神经网络是一门新兴的学科，作为一种多输入、多输出的非线性系统，凭借其联想、记忆、自适应等特性在预测仿真领域受到了广泛的重视。孙登月等[6]采用 BP神经网络对冷连轧机出口厚度进行了快速预报，轧件的出口厚度预报精度控制在-5%~5%以内。刘东东等[7]采用RBF神经网络对热连轧精轧钢板厚度进行了快速预报，厚度误差控制在-0.15~0.15 mm以内。王艾伦等[8]采用BP神经网络和弹跳方程相结合的方法对铝热连轧厚度进行了预测，轧件的出口厚度预报精度控制在-1%~1%以内。由于GRNN网络在函数逼近能力和学习速度上较 BP网络有着较强的优势，预测结果也较好，与BP网络相比，GRNN网络中需要调整的参数比较少，只有1个光滑因子，因此，可以更快地找到合适的预测网络，预测精度也比较高。因此，GRNN网络模型非常适用于中厚板轧机厚度的预测[9]。

1 GRNN神经网络建模

1.1 GRNN神经网络的结构

GRNN网络是Sprecht在1991年提出的，是一种通用的非参数回归模型。它作为径向基函数神经网络(RBF)的一个分支，是基于非线性回归理论的前馈型神经网络，它通过激活神经元来逼近函数。

GRNN网络的结构分为输入层、隐含层和线性输出层，其网络结构与径向基网络相似，如图1所示[10]。

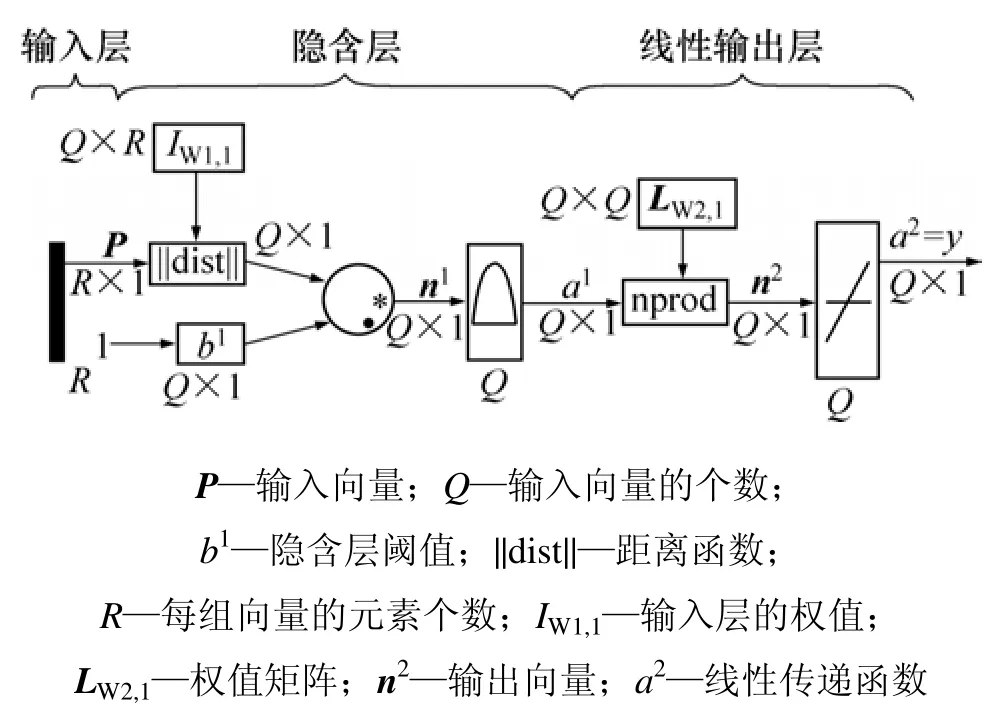
图1 GRNN神经网络结构示意图Fig.1 GRNN neural network structure

1.2 轧件厚度误差的来源及分析

在轧制力的作用下，轧件发生变形，其外形尺寸和断面形状发生变化[11-12]。轧件的反作用力也使轧机的工作机座产生弹性变形。通常将轧机工作机座产生的弹性变形的总和称为轧机的弹跳值[13]。轧机机座的弹性变形如图2所示。在轧制力的作用下，工作机座产生弹性变形，轧件的厚度大于初始辊缝值，并且沿着轧件宽度方向的厚度分布不均匀[14]。

图2 机座弹性变形示意图Fig.2 Elastic deformation of rolling mill stand

影响轧件出口厚度的主要因素有：轧件的温度、轧制速度、压下量、厚度、轧制力等。这些因素对轧件出口厚度的影响较大。此外，轧辊磨损、轧辊的热胀冷缩、轧辊平衡力的波动、轧辊偏心、轧辊润滑剂膜层厚度的变化等因素对轧件出口厚度也有一定的影响。

1.3 训练样本的获取与标准化

根据某厂4200轧机轧制45号钢的实测数据，确定网络模型的输入层有7个输入量，它们分别是轧辊初始辊缝、轧制温度、轧制速度、压下量、轧件的入口厚度、轧制前的宽度以及轧制力。为了简化网络，提高学习和训练的速度，在上述输入参量中没有包括轧机工作辊直径、支承辊直径、轧机刚度、轧辊凸度和乳化液流量等因素，这是因为它们的变化相对稳定。输出层只有1个输出量，即轧件本道次的出口厚度。

训练样本的选取需要注意代表性和实际问题自身的特点，合理进行选择。本文选取的方法是：首先去除少数误差明显较大的数据，然后，采用等距离取样的方法选取(如每隔3个数据选取1个数据等)。

经过筛选，本文选取其中135组实验数据作为训练样本。在训练前，训练样本要进行归一化处理，即把数据归一化到[0, 1]之间。具体的做法是：令一组数中的最大值为 xmax，最小值为 xmin，则归一化后的 x0和初始x的关系式为：

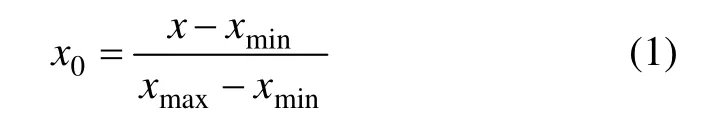
1.4 GRNN神经网络模型的建立

宽度系数对网络的性能影响比较大。宽度系数越大，网络对样本数据的逼近过程就越光滑，但是，逼近误差比较大；宽度系数越小，网络对样本的逼近性能就越好，但是，逼近过程就越不光滑，还有可能出现过拟合现象。由于实验和测量都有误差，而本文所设定的训练误差已经很小，为了防止出现过拟合现象，不宜选取过小的宽度系数[15]。

选取训练样本以外的15组测试样本，分别选取宽度系数为0.3，0.4，0.5，0.6和0.7进行试验，其预测误差如图3所示。由图3可见：当取不同的宽度系数时，GRNN网络对测试样本的预测误差趋势相同，只是误差不同。

图3所示的相对误差是将网络的输出数据反归一化后与实验数据相比较得到的。通过GRNN网络输出厚度和实测厚度相比较可知：当宽度系数为0.3时，相对误差都在-1%~1%以内，网络的预测误差较小，说明此时网络的精度很高，泛化能力较好。因此，选取宽度系数为0.3。

图3 不同宽度系数的预测误差Fig.3 Prediction errors of different spread values

2 GRNN网络的测试结果分析

GRNN网络预测的厚度误差如图4所示。由图4可见：厚度误差几乎都在-0.25~0.25 mm以内, 预测误差很小。因为测试样本不包含训练样本，所以，预测结果具有普遍意义。

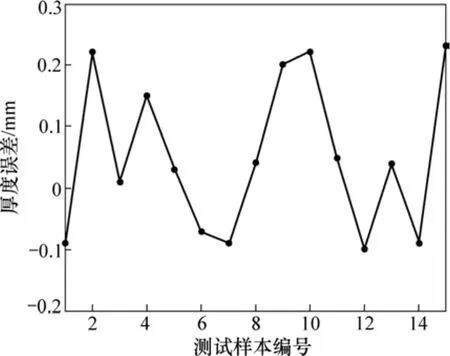
图4 GRNN神经网络的预测误差Fig.4 Prediction errors of GRNN neural network

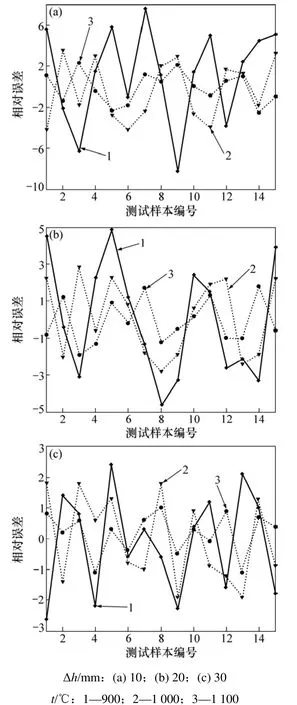
图5 不同压下量时的预测误差Fig.5 Prediction errors of different reductions

为了分析不同的轧制温度对 GRNN网络模型精度的影响，再分别选取压下量为10，20和30 mm，轧制温度分别为900，1 000和1 100 ℃的各15组数据，共建立9个GRNN网络模型，网络的训练和测试都采用宽度系数0.3。将得到的9组相对误差按压下量的不同分为3组，如图5所示。从图5可见：在压下量Δh相同，轧制温度t为900 ℃时的预测误差最小；随着轧制温度的升高，网络的预测误差逐渐增大。

为了分析不同压下量对 GRNN网络模型精度的影响，将上述得到的9组相对误差按轧制温度的不同分为3组，如图6所示。由图6可见：在轧制温度t相同的情况下，压下量Δh为10 mm时网络模型的预测误差最大；随着压下量的增加，网络的预测误差逐渐减小。

根据生产实践经验，轧机的弹性变形和轧制力之间呈非线性关系。当轧制力较小时，机座的弹性变形和轧制力之间的非线性关系较为明显；当轧制力较大时，机座的弹性变形和轧制力趋近于线性。产生这种现象的主要原因是零部件之间存在接触变形和间隙，并且非线性区不是很稳定。当轧制温度较低或者压下量较大时，轧制力较大。而轧制力是影响轧件厚度的1个主要因素，当轧制力较大时，其他因素对轧件厚度误差的影响减少，因此，GRNN网络的预测误差较小。

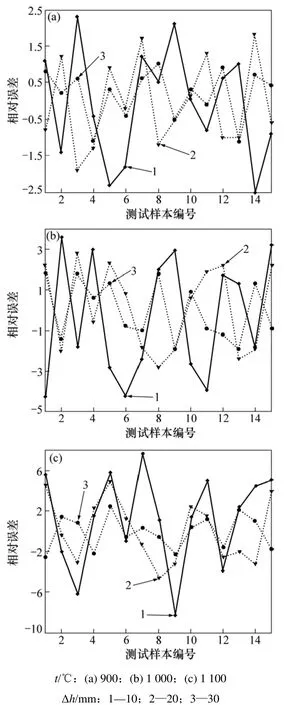
图6 轧制温度不同时的预测误差Fig.6 Prediction errors of different rolling temperatures

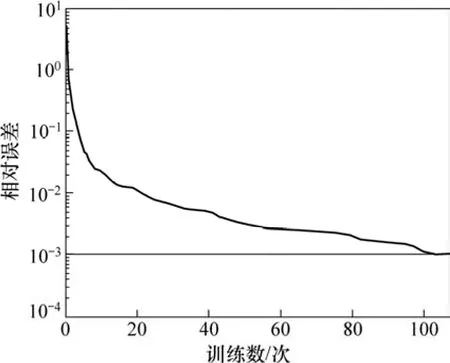
图7 BP网络的训练过程Fig.7 Training process of BP network

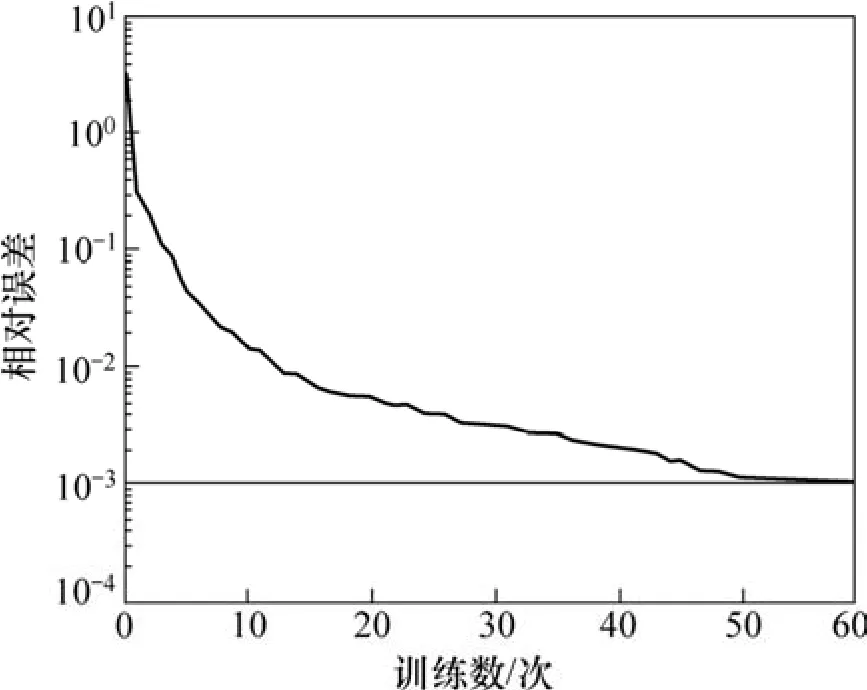
图8 Elman网络的训练过程Fig.8 Training process of Elman network

3 3种网络预测误差的对比

为了与BP网络和Elman网络相比较，本文又设计了中厚板轧机厚度预测的BP网络和Elman网络模型，输入层参数与GRNN网络的相同，都为7个，输出层节点数为1个，网络的目标误差设定为0.001。根据Kolmogorov定理，在3层神经网络中，隐含层神经元个数 n2和输入层神经元个数 n1之间有以下近似关系：

因此，隐含层节点数确定为15个，它们的训练过程如图7和图8所示。由图7可知：BP网络经过107步训练，误差收敛到10-3。由图8可知：Elman网络经过59步训练，误差也收敛到10-3。BP网络、Elman网络及GRNN网络的预测误差如表1所示。由表1可以看出：BP网络的预测误差都在-6%~6%以内，Elman网络的预测误差都在-4%~4%以内，GRNN网络的预测误差都在-1%~1%以内，这说明GRNN网络的预测精度要比BP网络和Elman网络的高。另外，由训练过程可知，BP网络和Elman网络不稳定，而GRNN网络很稳定，这说明GRNN网络的稳定性比BP网络和Elman网络的强。

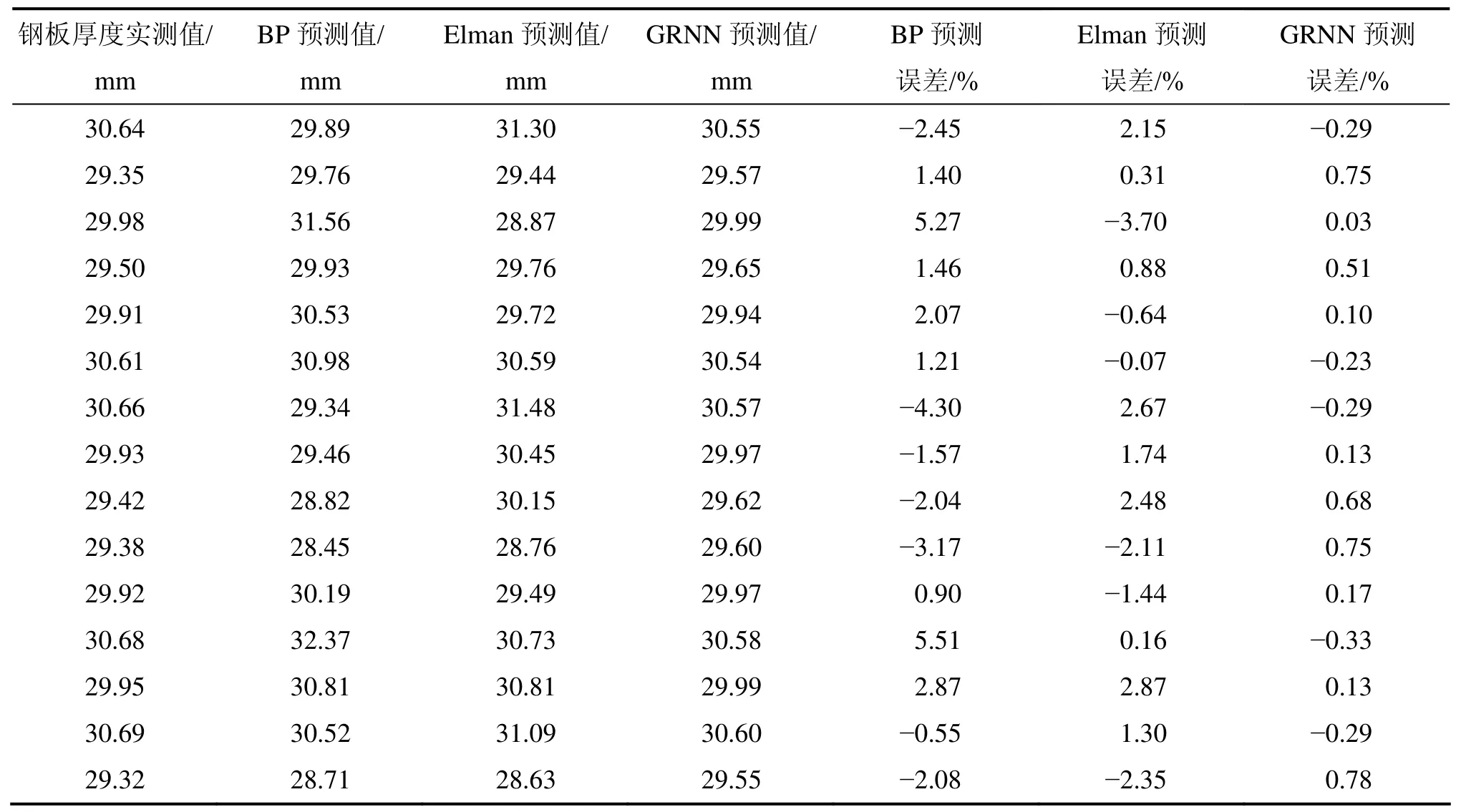
表1 3个网络的预测误差Table1 Prediction errors of three neural networks

4 结论

(1) GRNN网络能够综合反映影响轧件厚度的各种因素，对轧件厚度的预测具有相当高的精度和较强的泛化能力，其相对误差都在-1%~1%以内。这表明该网络对轧件厚度的预测具有较好的预测能力和广阔的应用前景。

(2) 通过3个网络模型的对比，GRNN网络预测精度有一定提高。这对于中厚板轧机控制模型的建立和应用、提高板材质量，都是一个有益的尝试，对生产实践具有一定的指导意义。

(3) 为了简化网络，提高学习和训练的速度，本文在输入参量中没有包括变化相对稳定的因素。因此，本文所建立的GRNN网络只适用于4200轧机轧制45号钢时的厚度预测。当轧制工艺发生变化，或者在不同的轧机上轧制不同类型的钢板时，该网络还需要根据实际情况，重新进行训练和学习，以确定所对应状态的权值和阈值。

[1] 许健勇. 薄板冷轧厚度与板形高精度控制技术[J]. 钢铁, 2002,37(1): 73-77.

XU Jian-yong. High precision thickness and shape control technology for thin strip rolling[J]. Iron and Steel, 2002, 37(1):73-77.

[2] 周富强, 曹建国, 张杰, 等. 基于神经网络的冷连轧机轧制力预报模型[J]. 中南大学学报: 自然科学版, 2006, 37(6):1155-1160.

ZHOU Fu-qiang, CAO Jian-guo, ZHANG Jie, et al. Prediction model of rolling force for tandem cold rolling mill based on neural networks and mathematical models[J]. Journal of Central South University: Science and Technology, 2006, 37(6):1155-1160.

[3] 曹建国, 张杰, 陈先霖, 等. 宽带钢热连轧机板形设定的解耦与应用[J]. 钢铁, 2001, 36(4): 42-46.

CAO Jian-guo, ZHANG Jie, CHEN Xian-lin, et al. Decoupling in setup program of shape and gauge control system on finishing stand of hot strip mill Co[J]. Iron and Steel, 2001, 36(4): 42-46.

[4] 胡贤磊, 王昭东, 王君, 等. 中厚板轧机弹跳模型的数值分析和应用[J]. 钢铁, 2004, 39(5): 38-42.

HU Xian-lei, WANG Zhao-dong, WANG Jun, et al. Numeric analysis and application of stiffness model for plate mill[J]. Iron and Steel, 2004, 39(5): 38-42.

[5] 王昭东, 田勇, 赵忠, 等. 中厚板厚度控制模型的自学习[J].东北大学学报: 自然科学版, 2006, 27(7): 771-774.

WANG Zhao-dong, TIAN Yong, ZHAO Zhong, et al.Self-Learning of gauge control model for plate rolling[J]. Journal of Northeastern University: Science and Technology, 2006, 27(7):771-774.

[6] 孙登月, 杜凤山, 朱光明, 等. 冷连轧机出口厚度人工神经网络快速预报[J]. 燕山大学学报, 2003, 27(1): 51-53.

SUN Deng-yue, DU Feng-shan, ZHU Guang-ming, et al.Prediction on thickness of cold continuous rolling mill using neural network[J]. Journal of Yanshan University, 2003, 27(1):51-53.

[7] 刘东东, 王焱. 基于 RBF神经网络的热连轧精轧厚度的预报[J]. 济南大学学报: 自然科学版, 2006, 20(4): 312-314.

LIU Dong-dong, WANG Yan. Prediction of rolling thickness based on RBF neural network[J]. Journal of Jinan University:Science and Technology, 2006, 20(4): 312-314.

[8] 王艾伦, 舒畅. BP神经网络和弹跳方程在铝热连轧厚度预报中的综合应用[J]. 铝加工, 2007(1): 5-9.

WANG Ai-lun, SHU Chang. Application of neural network and spring equation to thickness prediction in aluminum hot tandem rolling[J]. Aluminum Processing, 2007(1): 5-9.

[9] 孟令启, 李成. 中厚板轧机测量测试与力学行为建摸[M]. 郑州: 黄河水利出版社, 2006: 205-218.

MENG Ling-qi, LI Cheng. Plate mill test and measurement of the mechanical behavior modeling[M]. Zhengzhou: Yellow River Water Conservancy Press, 2006: 205-218.

[10] 闻新, 周露, 李翔. MATLAB神经网络仿真与应用[M]. 北京:科学出版社, 2003: 288-289.

WEN Xin, ZHOU Lu, LI Xiang, et al. MATLAB neural network simulation and application[M]. Beijing: Science Press, 2003:288-289.

[11] 刘相华, 胡贤磊, 杜林秀, 等. 轧制参数计算模型及其应用[M]. 北京: 化学工业出版社, 2007: 96-103.

LIU Xiang-hua, HU Xian-lei, DU Lin-xiu, et al. Rolling parameters model and application[M]. Beijing: Chemical Industry Press, 2007: 96-103.

[12] 孟延军. 轧钢基础知识[M]. 北京: 冶金工业出版社, 2005:273-280.

MENG Yan-jun. Rolling basics knowledge[M]. Beijing:Metallurgy Industry Press, 2005: 273-280.

[13] 马金亮, 孟令启, 张洛明, 等. 基于Matlab优化工具箱的中厚板轧机结构参数设计[J]. 机械工程师, 2006(11): 94-96.

MA Jin-liang, MENG Ling-qi, ZHANG Luo-ming, et al.Optimum design of 4200 rolling mill based on matlab optimization toolbox[J]. Mechanical Engineer, 2006(11): 94-96.

[14] 邹家祥. 轧钢机械[M]. 北京: 冶金工业出版社, 2004:174-189.

ZOU Jia-xiang. Rolling mill mechanic[M]. Beijing:Metallurgical Industry Press, 2004: 174-189.

[15] 飞思科技产品研发中心. 神经网络理论与 MATLAB 7实现[M]. 北京: 电子工业出版社, 2005: 123-125.

Product Center of Feisi Technology. Neural network theory and the realization of MATLAB 7[M]. Beijing: Electronics Industry Press, 2005: 123-125.