对运动目标约束的机载前视阵雷达杂波谱补偿方法
2011-05-29刘锦辉廖桂生
刘锦辉 廖桂生 李 明
(西安电子科技大学雷达信号处理国家重点实验室,陕西 西安 710071)
1.引 言
空时自适应处理(STAP)[1-4]常用来抑制杂波,检测慢速目标,其杂波抑制性能取决于杂波协方差矩阵的估计精度。对于机载前视阵雷达,由于杂波空时分布存在严重的距离依赖性[5-6],使得独立同分布的样本数急剧减少,导致杂波协方差矩阵估计不准确,进而使得STAP处理器的杂波抑制性能下降严重。如何补偿杂波的距离依赖性是机载前视阵雷达信号处理中非常重要的问题。
针对机载前视阵雷达地面杂波的距离依赖性问题,国内外学者进行了大量的研究。杂波距离依赖性补偿方法主要有多普勒搬移法[7](DW);角度多普勒补偿法[8](ADC);自适应角度多普勒补偿法[9](A2DC);导数更新法[10](DBU)。这些方法通过在多普勒域或波束域对训练距离单元进行补偿,使得这些距离单元杂波的空时分布与参考距离单元趋于一致,达到补偿杂波距离依赖性的目的,然而这些方法只是对主杂波点进行单点补偿。基于配准的补偿方法[11](RBC)是一种新的全谱域补偿方法,该方法根据杂波谱的先验信息通过原始回波数据构造出杂波分布的相关矩阵,然后通过对构造出的相关矩阵的变换使得训练距离单元和参考距离单元的杂波数据的统计特性趋于一致,从而实现对地面杂波距离依赖性的补偿。然而,机载雷达在进行运动目标检测时,为了确保目标检测的实时性,常用一组空时自适应权矢量对一段距离的杂波数据进行处理。使用RBC方法的变换矩阵对这些距离单元杂波进行距离依赖性补偿后,会使得变换后的各距离单元中运动目标信息在空时平面上散开,致使这些距离单元中的运动目标无法被检测。
针对该问题,提出一种运动目标信息约束的杂波补偿方法,该方法在基于配准的补偿方法中根据动目标与杂波的多普勒频率不同来添加运动目标约束保护。通过该方法求解的变换矩阵一方面能够有效地降低杂波数据的距离依赖性,另外能够对包含在杂波中的运动目标信息起到保护作用。计算机仿真结果验证了该方法的有效性。
2.前视阵雷达杂波信号模型和距离依赖性分析
图1给出了机载前视阵雷达的几何关系图。其中,载机R的高度为H,速度为VR,载机速度方向与天线A的阵面轴向夹角为α;S是斜距为RS的距离门上的杂波散射点,它的空域锥角和速度锥角分别为ψS和ψd,方位角和俯仰角分别为θ和φ.

图1 机载前视阵雷达模型
杂波散射点S处归一化的多普勒频率fd为
(1)
式中:fprf为发射脉冲的重复频率;λ为发射信号的波长。
由式(1)通过数学变换可以得出空域锥角和多普勒频率之间的关系[5]为
(2)

在机载前视阵情况下,α=90°,式(2)可以化简为
(3)
在考虑地球半径Re影响的情况下,俯仰角φ可表示为
(4)
由式(3)可知,机载前视阵雷达的杂波分布为正椭圆;另外,由于俯仰角φ是斜距RS的函数,不同距离门的杂波在空时平面上分布也不同。这种杂波空时分布随斜距变化的现象称为杂波的距离依赖性。
图2给出了载机高度为6 km时,不同距离环上的杂波空时分布曲线。

图2 机载前视阵杂波方位多普勒分布
从图2可以看出,斜距为6.3 km、7.5 km、10 km这三个近程的杂波空时分布随距离变化很大;斜距为30 km、50 km、100 km的远程杂波的空时分布基本上趋于一致。由上可知,杂波的距离依赖性主要表现在近程距离门的回波数据中,这主要是因为近程距离门的俯仰角余弦变化和远处相比,非常剧烈,从而导致近程杂波的距离依赖性表现的更加明显。
由图1的杂波模型可知,斜距为RS的第l个距离门接收的地面杂波数据Xl是对方位角在0到π之间(不考虑天线背面的杂波)的杂波散射点回波数据的积分,即
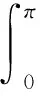
(5)
式中: ⊗表示向量的Kronecker积;βl(θ)为杂波散射点S(方位角为θ)对应的幅度值;nl为回波数据中的噪声分量;N和K表示接收通道数和采样脉冲数;b(vd(θ))和a(vS(θ))为散射点S对应的时域导向矢量和空域导向矢量,分别为
b(vd(θ))=[1,ej2πfd,…,ej2π(K-1)fd]T
(6)
(7)
式中:d为阵元间距; (·)T为转置运算。
βl(θ)代表雷达方程中杂波散射点幅度,它与杂波散射点的散射截面积、距离门斜距、发射天线和接收天线的增益等因素有关。
3.运动目标约束的杂波谱补偿方法
由杂波数据模型的表达式(5)可知,通过机载前视阵雷达的先验信息,在获取杂波散射点的幅度及其在空时平面的位置之后便可以实现对杂波数据的估计。RBC方法通过对某一距离单元接收的回波数据进行子孔径平滑[12],从该距离单元获取足够多的样本,估计出该距离单元的杂波协方差矩阵;在该距离单元的空时分布上取一些离散的点,使用估计的协方差矩阵计算这些点处的Capon谱,以此作为这些点的幅度值,按照式(5)对这些点进行求和实现对该距离门数据的重构。RBC方法通过重构的距离单元数据求解变换矩阵,使得训练距离单元数据向参考距离单元配准,实现对杂波距离依赖性的补偿。当杂波数据中包含有运动目标时,使用该方法对杂波补偿后,包含在杂波中的运动目标信息会在空时平面上散开,导致运动目标无法检测。在RBC方法基础上,提出一种新的杂波谱补偿方法,该方法在求解变换矩阵表达式中添加运动目标信息的保护约束,使得求解的变换矩阵不但能够对杂波谱的距离依赖性进行补偿,而且能够确保包含在杂波中的运动目标信息不发生改变。
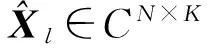
(8)

r=1,…,N-G+1;t=1,…,K-J+1
(9)
在对Xl进行空时子孔径平滑后得到的样本数据都来自同一个距离门,因此这些样本数据不存在距离依赖性;可以通过这些样本数据获得该距离门在子孔径下的协方差矩阵估计RSl∈CJG×JG,其为
(10)
式中: (·)H表示共轭转置; Vec(·)是将矩阵做如下操作:将矩阵的第二列放在第一列下面;第三列放在第二列下面,以此类推将矩阵变换成一个列矢量。
在第l个距离门的角度多普勒分布曲线上均匀的取P个离散点(P>2NK)[13],wSi和wdi分别为该距离门的角度多普勒分布曲线上第i个离散点处的空域角频率和时域角频率(i=1,…,P)。由于杂波的Capon谱能够反应出杂波功率谱的强度,因此,可以使用(wSi,wdi)点处杂波的Capon谱P(wSi,wdi)来代表该点处的杂波散射系数来重构该点处的杂波数据。
i=1,…,P
(11)
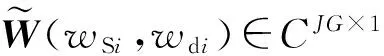

(1,ejwSi,…,ej(G-1)wSi)T
(12)
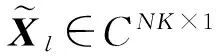
(13)
WH(wSi,wdi)
(14)
式中:W(wSi,wdi)∈CNK×1为空时平面上离散点(wSi,wdi)的空时导向矢量,且有
W(wSi,wdi)=(1,ejwdi,…,ej(K-1)wdi)T⊗
(1,ejwSi,…,ej(N-1)wSi)T
(15)

(16)
由文献[14]可知,式(16)的优化问题可以转化为
(17)

求解式(17)可得
(18)
将式(18)求解的Tl作用于雷达接收的回波数据,可以保证训练距离单元和参考距离单元杂波数据统计特性趋于一致,实现对杂波数据距离依赖性的补偿。
当接收的雷达回波数据中包含运动目标时,直接使用上面的方法进行杂波谱补偿,会导致运动目标无法检测。针对此问题,在上述方法中添加运动目标信息保护的约束,使得在补偿杂波距离依赖性的同时,对运动目标信息进行保护。
由于运动目标检测主要关心的是主波束内是否存在运动目标,而且主波束宽度一般比较窄,因此,主波束内动目标空域指向可以用主波束指向ws表示;由于动目标的多普勒信息无法获取,并且运动目标的多普勒与杂波多普勒在空时平面上是不同的,因此,在除杂波多普勒分布之外的多普勒域上取M个离散的多普勒频率点,构造运动目标空时响应矩阵VT∈CNK×M来约束运动目标。
(19)
式中:wS为目标方向的空域角频率;wd1,wd2,…,wdM是在多普勒域上均匀取的M个多普勒频率点。由于实际中,主波束有一定的宽度,为了提高目标约束的稳健性,可以在构造VT时,将主波束方向附近的波束指向考虑进来。
构造以下的目标函数来求解Tl∈CNK×NK,
(20)
式(20)在对杂波进行基于配准的距离依赖性补偿同时,增加了对包含在杂波数据中的运动目标信息的约束保护,这样可以保证求解的变换矩阵Tl在对杂波距离依赖性补偿的同时,对主波束内的运动目标信息进行保护。
式(20)是一个优化问题,解为

(21)
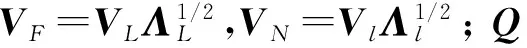

(22)


(23)
通过式(21)求解的Tl不仅能够对杂波数据进行距离依赖性补偿,保证训练距离门数据和参考距离门杂波数据的统计特性趋于一致,而且能够对杂波数据中的运动目标信息进行有效的保护。
使用Tl对接收数据进行处理,得到的数据Yl∈CNK×1为
Yl=TlXl,l=1,…,L-1
(24)
处理后的统计协方差矩阵RL∈CNK×NK为
(25)
通过本文方法处理后的杂波的距离依赖性能够得到有效的减小,并且包含在杂波中的运动目标信息能够得到保护。使用式(25)获得补偿后的杂波协方差矩阵,进行空时自适应处理来抑制杂波,限于篇幅,这里不做讨论。
4.计算机仿真
机载前视阵雷达的仿真参数如表1所示。

表1 前视阵雷达仿真参数
机载前视阵雷达接收的回波数据的起始距离单元的斜距为7.5 km,距离门的间距为30 m.
图3是使用基于配准的补偿方法对机载前视阵雷达地面杂波数据补偿前后杂波的功率谱以及最优空时处理器的改善因子。由图3(a)可以看出,机载前视阵雷达地面杂波存在距离依赖性,杂波功率谱在空时两维平面上发生展宽,使得杂波周围可检测的慢速目标性能下降。使用基于配准的补偿方法处理后,地面杂波功率谱明显变窄,这对于检测杂波附近的低速运动目标非常有利。从图3(c)可以看出,使用基于配准的补偿方法处理后,主瓣杂波处的改善因子的凹口变窄,最优空时处理器的性能在主波束附近有50 dB左右的改善。
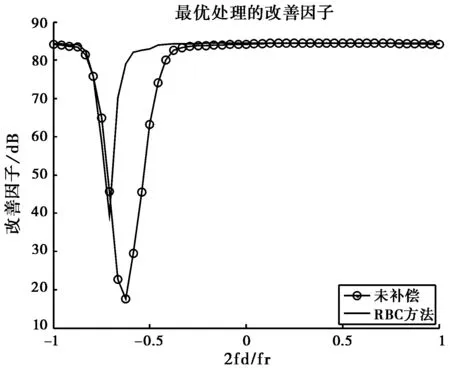
(c) 最优处理器的改善因子图3 基于配准的补偿方法
在雷达接收回波数据的第250个距离门,阵面法线方向注入归一化多普勒为-0.1的运动目标。
图4给出了使用RBC方法和本文方法对含有运动目标的杂波进行处理的功率谱图。使用RBC方法对图4(a)的杂波数据进行处理得到的杂波空时杂波谱如图4(b)所示,图4(b)中杂波的多普勒分布明显变窄,但是图4(a)中的动目标信息在图4(b)中散开,在空时平面上已经无法检测,这是因为通过RBC方法求解的变换矩阵在对杂波距离依赖性补偿时,无法对运动目标进行有效的保护,导致运动目标信息在空时平面散开。图4(c)为使用本文方法处理后的杂波功率谱图,杂波的距离依赖性得到很好的补偿,杂波多普勒分布明显变窄,另外,杂波中的运动目标也得到很好的保护,这充分说明本文方法在对杂波距离依赖性补偿同时能够对包含在杂波数据中的动目标进行保护的有效性。
图5通过本文方法处理前后杂波数据的距离多普勒图说明本文方法的有效性。图4(a)为处理前的杂波,第0到400号近程距离门的杂波多普勒分布在0到-1000 Hz之间,而第400到600号远程距离门杂波分布在-600到-1000 Hz,可以看出:距离依赖性导致杂波多普勒分布展宽主要表现在近程杂波,远程杂波的多普勒展宽很小。使用本文方法处理后,近程杂波多普勒分布明显变窄,杂波功率降低,这主要是由于本文的补偿方法将近程距离门杂波数据通过变换矩阵向远程距离门进行配准,由于远程杂波幅度较低,变换之后,近程数据幅度也变小;包含在第250号距离门的运动目标经过本文方法处理后,依然能够保留下来,但是运动目标的能量有所降低。对比图5(a)和(b)说明本文方法在对杂波距离依赖性补偿以及运动目标信息保护的有效性。
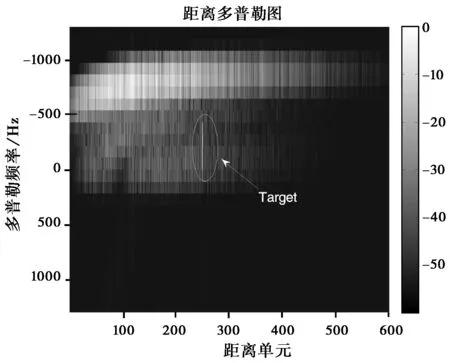
(a) 含动目标的杂波

(b) 本文方法处理效果图5 杂波的距离多普勒图
5.结 论
机载前视阵雷达杂波空时分布具有距离依赖性,基于配准的补偿方法能够有效地对杂波的距离依赖性进行补偿;然而,当杂波数据中存在运动目标时,使用该方法处理后,包含在杂波中的运动目标信息在空时平面上散开,导致其无法检测。针对此问题,本文提出一种运动目标约束的杂波谱补偿方法,该方法在基于配准的补偿方法中添加运动目标的空时响应约束,对杂波数据中的运动目标信息进行保护。使用本文的方法对机载前视阵雷达回波数据进行处理,一方面,杂波的距离依赖性得到有效的补偿;另外,地面杂波数据中的运动目标信息得到很好的保护。计算机仿真结果验证了本文提出方法的有效性。
[1] BRENNA L E, REED I S. Theory of adaptive radar [J]. IEEE Trans AES, 1973, 9(2): 237-252.
[2] 王永良,彭应宁. 空时自适应信号处理[M]. 北京: 清华大学出版社, 2000: 26-94.
[3] 何 洁, 冯大政, 向 聪, 等. 基于M-CAP的三维空时自适应降维算法[J]. 电波科学学报, 2010, 25(4): 696-701.
HE Jie, FENG Dazheng, XIANG Cong, et al. Reduced-dimension 3D STAP method based on M-CAP[J]. Chinese Journal of Radio Science, 2010, 25(4): 696-701. (in Chinese)
[4] WU J, WANG T, MENG X, et al. Clutter suppression for airborne non-sidelooking radar using ERCB-STAP algorithm[J]. IET Radar, Sonar and Navigation, 2010, 4(4): 497-506.
[5] 姜 晖, 廖桂生. 基于相似性度量的非正侧阵杂波谱补偿方法[J]. 电波科学学报, 2009, 24(6): 1078-1081.
JIANG Hui, LIAO Guisheng. An approach for clutter spectrum compensation based similar measure [J]. Chinese Journal of Radio Science, 2009, 24(6): 1078-1081. (in Chinese)
[6] 王万林, 廖桂生, 张广斌. 相控阵AEW雷达杂波抑制的非均匀处理方法研究[J]. 电波科学学报, 2004, 19(3): 348-353.
WANG Wanlin, LIAO Guisheng, ZHANG Guangbin. Study on STAP in non-homogeneous environment for phased array early warning radar [J]. Chinese Journal of Radio Science, 2004, 19(3): 348-353. (in Chinese)
[7] KREYENKAMP O, KLEMM R. Doppler compensation in forward looking STAP radar [J]. Proc. Inst. Elect. Eng. Radar, Sonar, Navigation, 2001, 148(1): 596-608.
[8] HIMED B, ZHANG Y, HAJJARI A. STAP with angle-Doppler compensation for bistatic airborne radars[C]// Processing of 2002 IEEE Radar Conference USA: IEEE. 2002: 311-317.
[9] MELVIN W L, HIMED B, DAVIS M E. Doubly adaptive bistatic clutter filtering[C]// IEEE National Radar Conference. Huntsville: IEEE, 2003: 171-178.
[10]HAYWARD S D. Adaptive beamforming for rapidly moving arrays[C]//Proc. Int. Conf. on ASSP,1996:1165-1168.
[11]LAPIERRE F D, DROOGENBROECK M V, VERLY J G. New methods for handling the range dependence of the clutter spectrum in non-sidelooking monostatic STAP radars[C]// ICASSP. Hong Kong,2003:73-76.
[12]PILLAI S, KIM Y, GUERCI J. Generalized forward/backward subaperture smoothing techniques for sample starved STAP[J]. IEEE Transactions on Signal Processing,2000,48(12):3569-3574.
[13]VARADARAJAN V, KROLIK J L. Joint space-time interpolation for distorted linear and bistatic array geometries[J]. IEEE Trans. on Signal Processing, 2006,54(3):848-860.
[14]LAPIERRE F D, RIES P, VERLY J G. Foundation for mitigating range dependence in radar space-time adaptive processing[J]. IET Radar, Sonar and Navigation,2009,3(1):18-29.
