基于图形处理器的时域有限差分算法硬件加速

张 波 薛正辉 任 武 李伟明 盛新庆

(北京理工大学信息与电子学院，北京 100081)

1.引 言

长久以来，作为微型计算机的核心硬件之一，CPU一直承担着绝大多数运算任务，也是传统数值计算软件面对的对象。而近年来，随着用户对于实时高解析率的图像处理需求的急剧增加，原本仅负责图形处理的图形处理器(GPU)呈现出惊人的发展趋势。发展至今，GPU的浮点处理能力及带宽已全面超越同期CPU，图1为CPU和使用开放图形程序接口(OpenGL)与计算统一设备架构(CUDA)GPU的扫描性能对比，可见GPU的浮点运算能力相较同期CPU具有突出的优势。

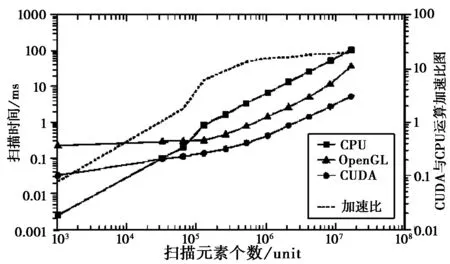
图1 CPU与GPU的计算性能对比

在计算能力突出的同时，GPU与CPU相比还兼具高度并行、多线程多核心等特点。电磁场数值计算若能有效利用GPU的计算能力及结构特点，无疑会极大提高运算速度和效率。

随着英伟达(Nvidia)公司在2002年提出可编程流处理器的概念以及在2006年推出CUDA运算架构，GPU运算能力的通用化在近年来取得了长足的发展。在计算电磁学领域，2004年Krakiwsky等人实现了GPU加速二维电磁场FDTD运算[1]，其后美国斯坦福大学和莱斯大学、加拿大卡尔加里大学的研究者广泛开展了利用GPU进行电磁场数值计算的研究[2-3]。2007年山东大学韩林等人开展了利用GPU结合网络并行运算技术的二维FDTD算法研究，以光波导器件为分析对象进行了探索[4]。2008年，电子科技大学刘瑜等人对GPU加速二维ADI-FDTD算法进行了研究[5]。同期的西南交通大学刘昆等人开展了GPU加速时域有限元的二维辐射计算研究[6-7]。然而迄今为止，GPU加速并未广泛运用于FDTD运算中，原因在于工程计算多面向三维空间，而三维FDTD计算的加速相较二维情况，在算法优化等方面提出了诸多新要求，对加速效率的要求也更加严格。如何针对GPU硬件架构选择适宜的FDTD算法进行优化，并且将三维空间中的激励源引入和吸收边界设置等流程高效地在GPU上得以实现，从而使得GPU加速FDTD运算真正进入工程应用阶段，是本文研究的问题。

2. GPU加速FDTD的原理

2.1 GPU硬件架构特点

GPU架构的突出特点是采用高度并行化的流处理器群作为运算单元，以Nvidia GT130M GPU为例，该GPU包含32个流处理器，以8个一组为单位组成4个流处理器群，处理器核心频率为600 MHz.与CPU运算体系中内存对应，GPU运算主要存储器为显存，按功能分为可被全部流处理器读写的全局显存、可被同一线程块内所有线程读写的线程共享显存以及单线程独享的线程显存。

2.2 GPU程序执行特点

与硬件架构相适应，GPU程序执行方式相比CPU程序并行化程度更高，更深入硬件层次。具体执行方式是以线程(Thread)为单位并行执行开发者编写的“Kernel”函数。详细流程是开发者编写执行计算任务的Kernel函数，规定函数执行的总线程数以及划分出线程网格(Grid)，线程网格会被细分为线程块(Block)后输送给GPU.GPU接到线程块以及Kernel函数后，自动将每个线程块以32个线程为一个单位(即一个Warp)进行划分，分配给多个流处理器群并行执行。

尽管GPU同时运行的线程数受其硬件能力制约，但Kernel函数的并发总线程数却可以远超出这一限制，这得益于GPU的Warp执行机制，即多个Warp可以轮流运行于多个流处理器群，甚至当某个流处理器群中的Warp处于等待状态时，它可以临时运行其他闲置的Warp.多线程多层面的并行机制极大提高了GPU的硬件利用率，同时GPU还提供了同一线程块中的线程间同步功能，可以有效地进行程序流程控制。

2.3 GPU与FDTD运算结合的优势

FDTD算法的场量更新机制非常适宜并行化。以FDTD算法中电场更新为例，求解某网格第n+1步电场E时，需读取的场值仅包括该网格第n步电场E及第n+1/2步时相邻网格的磁场H，这意味着场量更新过程对于各网格的空间更新次序不存在任何要求。这使得编写Kernel程序以及分割线程网格时，可以大幅偏重于线程执行效率的提高，而非保证线程的执行次序。

FDTD算法的算术指令符合流处理器的运算能力。GPU相较CPU而言，其运算能力的优势来源于多流处理器设计以及并行化的线程架构，就单个流处理器而言，它的单精度运算能力及精度并未达到同级别CPU的高度。相较其他电磁场数值算法，FDTD算法不采用矩阵运算，基本不涉及求幂求积分等计算，对GPU运算效率的提高和误差控制无疑十分有利。

3. GPU加速三维FDTD的计算模型

3.1 网格对应线程的划分及场量更新机制

以使用Nvidia Gt130M显卡计算56×56×120尺寸空间为例，由于显卡只有32个流处理器，4个流处理器群，而空间网格共有376320个，因此为每个网格分配一个线程既无必要也影响效率。在实际计算时，采取了一种“XY平面各点并行，Z向循环推进更新”的模式：将线程块大小设置为32×8，即Gt130M显卡所能支持的最大线程块大小，将XY平面的XY向网格数除以线程块对应维度大小并向上取整，得到线程网格大小为2×7，至此XY平面网格已一一映射为线程。在计算时，首先将所有线程指针指向Z=1时XY平面各点对应存储空间，在所有线程运算完成后，将每个线程指针指向Z向下一个网格进行新一轮计算，循环往复直至全空间更新完成。这种更新模式在提高多Warp执行机制效率的同时节省了运算资源。由于实际参与迭代运算的总线程数(32×8×2×7=3584)大于XY平面的网格数(56×56=3136)，每个线程在进行场量运算时，需要判断其对应网格是否处于求解范围内，若不处于求解范围内则不参与运算，否则显存读取地址会发生冲突进而导致计算结果出错。

3.2 FDTD算法的选择

对于并行FDTD算法，所有网格的场量更新采取同一类型运算公式有利于提高程序运行效率和进行误差控制分析。因此算法模型选择完全匹配层(UPML)作为吸收边界，并在包括UPML层的全空间内统一采取Taflove所提出的两步迭代法进行运算[8]，以Hx为例的场量更新公式见下式。

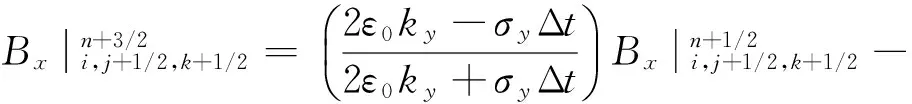
(1)

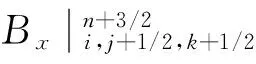
(2)

3.3 电磁参数的输入与优化

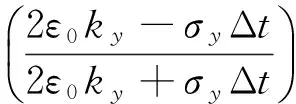
对于入射波的引入采取了总场/散射场法，当线程判断到其对应网格处于连接边界上时，会进行入射波引入或消去处理，这与CPU计算类似，因此不再赘述。

3.4 运算结果的存储输出

由于显存与内存之间的数据传输会占用可观的运算资源与时间，而FDTD计算结果往往只需要经空间与时间采样后的场量数据。因此GPU运算时尽量将采样后的数据存放于显存中，等待全部计算过程完毕后再进行输出，若采样时间点过多或采样面过大，会依据可用显存空间进行分次存储和输出，总体原则遵循在显存容量允许的情况下，尽可能减少GPU对内存空间的访问。

综上提出的GPU运算流程模型见图2。

图2 GPU运算流程模型

4.算例验证与分析

为验证提出的GPU加速流程模型，GPU加速运算被运用于实际工程问题的FDTD求解，并与CPU运算进行结果及性能比较。

4.1 算例与计算平台

算例模型为一个由尺寸为1.27 mm×12.7 mm，x向与y向单元间距均为17.8 mm的无限薄金属振子单元组成的频率选择表面。频率选择表面属于周期性结构，这里选用谱FDTD[9]配合周期性边界的方法，通过对一个单元建模计算进行分析。空间步长设置为0.318 mm，网格大小为56×56×120，x向与y向网格四周采取周期性边界条件进行处理，z向网格两端各设置10层UPML层作为吸收边界，单元模型放置于z=45截面中心并在z=75截面通过连接边界引入入射波。时间步长设置为5.295×10-13s，总共计算8192步。在计算过程中对z=85截面上场值进行时间采样，在全部时间步计算完成后，将采样结果通过傅里叶变换转换到频域并通过Poyinting定理求得横截面的功率函数，与入射波的对应功率函数相比后得到频率选择表面的功率反射系数。

计算过程采用两套GPU运算平台，GPU平台1为Nvidia GT130M图形处理器与512 MB显存，GPU平台2为Tesla C2050图形处理器与3 GB显存，CPU对比平台为Intel Core2 T6500处理器与3 GB内存，CPU与GPU运算的模型参数以及运算参数完全一致。

4.2 计算结果的精确性

为验证GPU加速的数值精确性，运算过程中抽取时间步t=1000时，y=30截面上Ey值进行输出比较，双GPU平台数值完全吻合，GPU平台计算结果与CPU平台符合很好如图3所示。

在全部时间步计算完成后，分别将GPU与CPU计算的结果进行后期处理，求出对应的功率反射系数，并与商业软件CST 2010计算所得结果进行比较。双GPU平台数值完全吻合，GPU平台与CPU平台运算结果对比见图4。

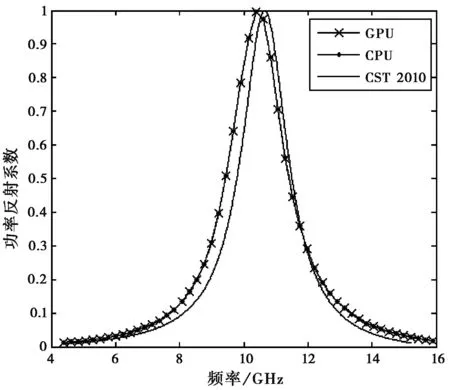
图4 功率反射系数对比图

由图4可见，GPU与CPU的计算结果吻合程度极佳，与CST软件所得结果也符合较好。通过后续计算比较，GPU计算所得功率反射系数与CPU计算结果之间差异仅为0.44%左右，足以满足绝大多数情况下工程需要。

4.3 加速性能分析

在计算过程中，将CPU平台与双GPU平台计算至同一时间步时所耗时间记录于表1。

表1 GPU与CPU计算耗时比

由表1可见，在整个运算过程中GPU平台的运算性能保持稳定，GPU平台1相对CPU平台加速比稳定在23倍以上，GPU平台2由于科学计算专用GPU的使用，加速比达到了174倍以上，有力证明了GPU加速FDTD运算的高效性。

5.总结与展望

通过对GPU加速FDTD算法的原理探讨与算例分析可以看到，计算流程中网格与线程的映射、算法的选择与优化、模型与入射波的输入、运算结果的存储等方面都在本文所提出的加速流程模型中得以高效实现。遵循这一流程的GPU加速FDTD运算，在满足运算精度需要的前提下，相较传统CPU运算，其运算速度大幅提高，不仅可以胜任大规模工程计算，适应性也极为优秀。在计算平台成本方面，算例中GPU平台1的芯片只是Nvidia显卡的中低端型号，目前主流Nvidia显卡都已经具备CUDA运算功能，这无疑大大降低了GPU加速FDTD的门槛，当需要进行大规模高性能科学计算时，可以使用GPU平台2中的专业级GPU芯片，相应加速比也更加优秀。

在GPU加速三维FDTD算法的可行性与高速性得到验证的同时，还有许多方面值得后继深入研究，例如FDTD网格与线程的对应是否有更高效的方式，GPU加速FDTD运算的误差分析与控制机理等等，这也是未来GPU加速FDTD研究的方向。

[1] KRAKIWSKY S E, TUMER L E, OKONIEWSKI M M. Acceleration of finite-difference time-domain (FDTD) using graphics processor units (GPU)[C]//IEEE MTTS International Microwave Symposium Digest, 2004, 2: 1033-1036.

[2] STEFANSKI T P, DRYSDALE T D. Acceleration of the 3D ADI-FDTD method using graphics processor units[J]. IEEE MTT-S International Microwave Symposium Digest (MTT), 2009, 1: 241-244.

[3] PRICE D K, HUMPHREY J R, KELMELIS E J. GPU-Based Accelerated 2D and 3D FDTD Solvers[J]. Physics and Simulation of Optoelectronic Devices XV, 2007, 6468(1): 22-25.

[4] 韩 林. 基于GPU的光波导器件FDTD并行算法研究[D]. 山东大学, 2007

LIN Han. GPU Based Optical Waveguide FDTD Parallel Research[D]. Shandong University, 2007. (in Chinese)

[5] 刘 瑜. FDTD算法的网络并行研究及其电磁应用[D]. 电子科技大学, 2008

LIU Yu. Parallel FDTD Algorithm Based on Network and Applications in Electromagnetic Problems[D]. University of Electronic Science and Technology of China, 2008. (in Chinese)

[6] 刘 昆, 王晓斌, 廖 成. 图形处理器(GPU)加速时域有限元的二维辐射计算[J]. 电波科学学报, 2008, 23(1): 111-114.

LIU Kun, WANG Xiaobin, LIAO Cheng. Acceleration of time-domain finite element 2-D radiation using graphics processor units(GPU)[J]. Chinese Journal of Radio Science, 2008, 23(1): 111-114. (in Chinese)

[7] 吴 霞, 周乐柱. 时域有限元法在计算电磁问题上的发展[J]. 电波科学学报, 2008, 23(6): 1208-1216.

WU Xia, ZHOU Lezhu. Application and development of time-domain finite element method on EM analysis[J]. Chinese Journal of Radio Science, 2008, 23(1): 1208-1216. (in Chinese)

[8] TAFLOVE A. Computational Electrodynamics: The Finite-Difference Time-Domain Method Third Edition[M]. Norwood MA: Artech House, 2005.

[9]AMINIAN A and RAHMAT-SAMII Y. Spectral FDTD: a novel technique for the analysis of oblique incident plane wave on periodic structures[J]. IEEE Transactions on Antennas and Propagation, 2006, 54(6): 1818-1525.