相控阵天线时域有限差分计算中激励源分析

姜彦南 李思敏 曹卫平 姜 兴 高 喜 于新华

(1. 桂林电子科技大学信息与通信学院，广西 桂林 541004; 2. 认知无线电与信息处理省部共建教育部重点实验室(桂林电子科技大学)，广西 桂林 541004)

1.引 言

在相控阵天线仿真分析中，人们多采用矩量法(MOM)进行数值计算，它是一种频率域的数值计算方法。但在对宽带天线的分析中，能一次性计算较宽频带电磁辐射特性的时域计算方法显示出其很大的优势，它首先获得近场或远场的时域波形，再通过傅里叶变换转化到频率域，用于分析宽频带天线辐射的电磁特性。在诸多时域计算方法中，于1966年由K. S. Yee[1]首次提出的时域有限差分(FDTD)方法采用时间和空间中心差分对Maxwell方程直接离散化，具有计算格式简单、空间和时间的物理过程直观等优点，已经在各种电磁和微波问题分析中得到广泛的应用[2]。

尽管目前FDTD方法已广泛用于研究天线电磁辐射特性问题[3-5]，但涉及偶极相控阵天线的仿真分析还存在一些问题，主要在于如何解决多个馈电单元数值计算过程中收敛速度太慢，以及在时域中如何合理设置各馈电激励源的相位等问题。这里针对上述问题进行探讨。

2.激励源的处理方法

在偶极天线的FDTD计算中，馈源多采用电压

源的励激方式[6-7]，该方式设置简单，物理意义清晰，直接作用于偶极天线的馈点缝隙处，特别适合于金属辐射单元的数值计算；求得电磁场值后，再根据安培环路定律，利用数值计算的磁场分量确定馈电点处的端口电流。

2.1 提高算法的收敛速度

FDTD数值计算要确定时间步数，时间步数的确定准则是在迭代计算结束时电磁场值收敛于0。在相控阵天线(特别是馈电单元很多的阵列天线)仿真过程中，由于辐射单元间的多次绕射和单元间的耦合[4]作用，使得FDTD数值计算经过很长时间步数仍不能满足收敛的要求，这就需要耗费大量的计算时间。

2.1.1 激励源模型

为了解决相控阵天线数值计算收敛速度慢的问题，首先是要克服单个偶极天线单元收敛慢的难题。在这方面Luebbers等人[8]做了前瞻性的研究，提出了一个能有效提高数值计算收敛速度的馈源模型——带有内电阻的偶极缝隙馈电激励源模型，如图 1所示。应用欧姆定律，在端口处电场分量为

(1)

式中：is,js,ks为激励源所处的位置；Vs为电压源激励信号，例如下面要提到的调制高斯脉冲信号；Rs

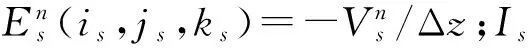
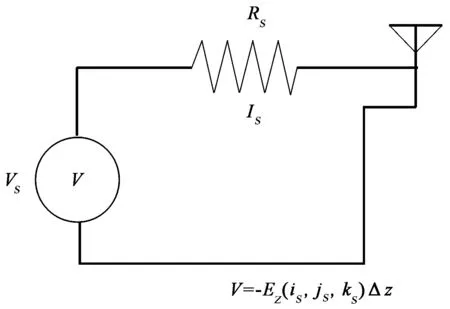
图1 具有内阻抗的电压源模型

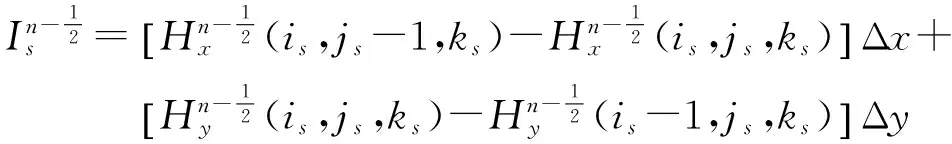
天线端口的有效输入电压为V=-Ez(is,js,ks)Δz；Δx,Δy和Δz为Yee元胞尺寸，Δz也是偶极馈电端口缝隙大小。

2.1.2 激励信号函数类型的选择

此外，激励信号函数类型的选择也是提高FDTD仿真收敛速度的一个重要方面。为分析天线的宽频带电磁特性，就需要选择覆盖考察频段的激励信号。常用的宽频带激励信号形式有高斯脉冲、微分高斯脉冲、调制高斯脉冲[9]、矩形调制脉冲[10]等。

从各信号的频率域响应[9]可以看出，高斯脉冲信号的直流分量很大，作为激励源可能会造成电荷积累，从而也会造成电磁场数值解收敛慢。而微分高斯脉冲和调制高斯脉冲则消除了直流分量，时域特性也比较简单，同时可以覆盖所要研究的频段范围，因此在天线分析中多有应用。但调制高斯脉冲相对微分高斯脉冲具有可以构造带通信号的优点，可以把信号调制到所希望的频段范围，具有更大的自由度，产生的频谱也容易控制。

综上所述，在相控阵天线中，对每一个辐射单元的馈电端口处均采用带有内电阻的偶极子缝隙馈电激励源模型，可有效地解决多个辐射单元间的多次绕射及单元间耦合所造成的收敛速度过慢的问题；而信号函数类型则选用不含直流分量且自由度较大的调制高斯脉冲信号对各馈电端口进行激励。

2.2 激励相位设置

相位是频率域中的参数，在诸如MOM等频域数值算法中，直接在激励源处设置其相位即可。而FDTD方法是在时域中实现电磁场的空间迭代计算，如何在时域激励信号中完成各馈电端口的相位设置，是时域方法能否正确处理相控阵天线的一个关键技术。

对于时域激励信号f(t)，其频率域响应为F(ω)，则频率域与时间域表达式满足下面时移特性[11]关系：

F(ω)⟺f(t)

exp(-jωΔt)F(ω)⟺f(t-Δt)

也就是说为实现Δφ=ωΔt的相位差，在时间域中的信号要有Δt的时间延迟，相应的延迟时长是

(2)

式(2)说明，时域信号经过Δt的时间延迟后，其幅度谱不变，相位谱产生附加相位值Δφ.从式(2)还可看出，对于不同的考察频率f，要实现相同的相位控制所需延迟时长不同。为分析天线不同频率的辐射特性，需要设置不同的延迟时长。

3.算例验证及分析

算例1：二元相控阵天线，模型如图 2(a)所示。

计算频率f=300 MHz，振子单元长度为λ/2，间距为λ/4。激励端口1(x=-λ/8)和2(x=+λ/8)，等副调相馈电，相位分别为0°和90°。偶极缝隙馈电各激励端口的内电阻Rs=50 Ω.

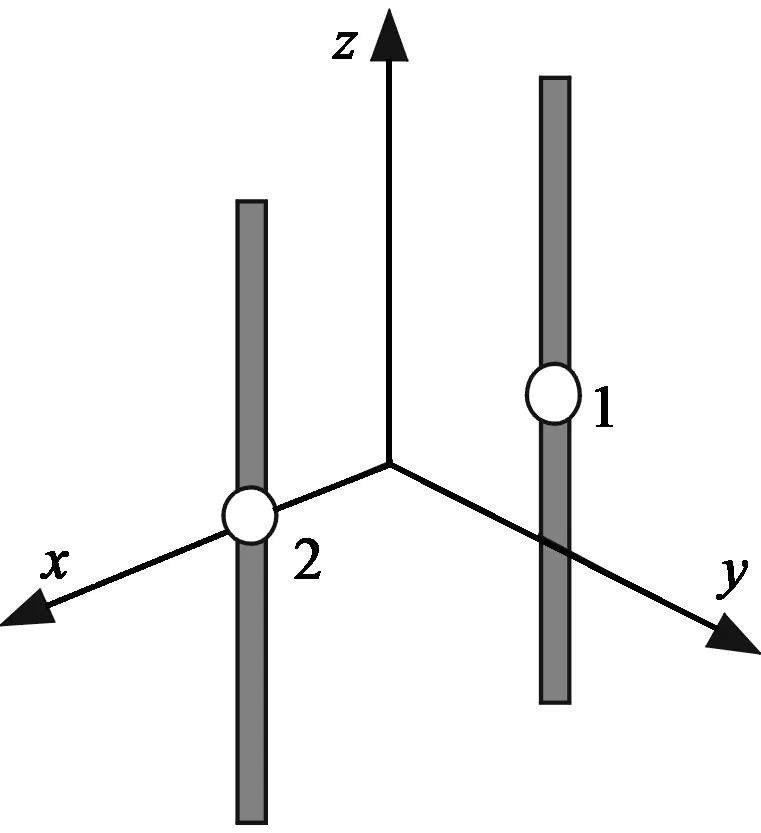
(a) 二元阵

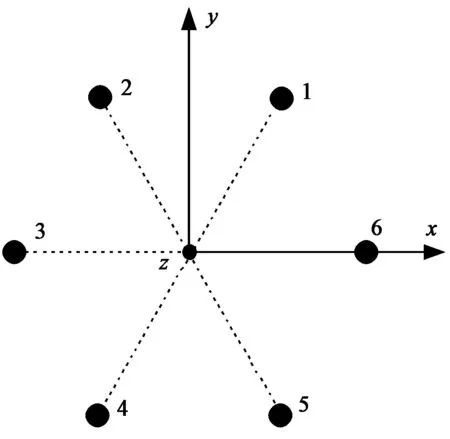
(b) 六元阵图2 相控阵天线模型

馈电的调制高斯脉冲电压激励信号如图 3所示。可以看出，两端口信号时差为Δt，这就是公式(2)得到的延迟时长Δt=0.833 ns.

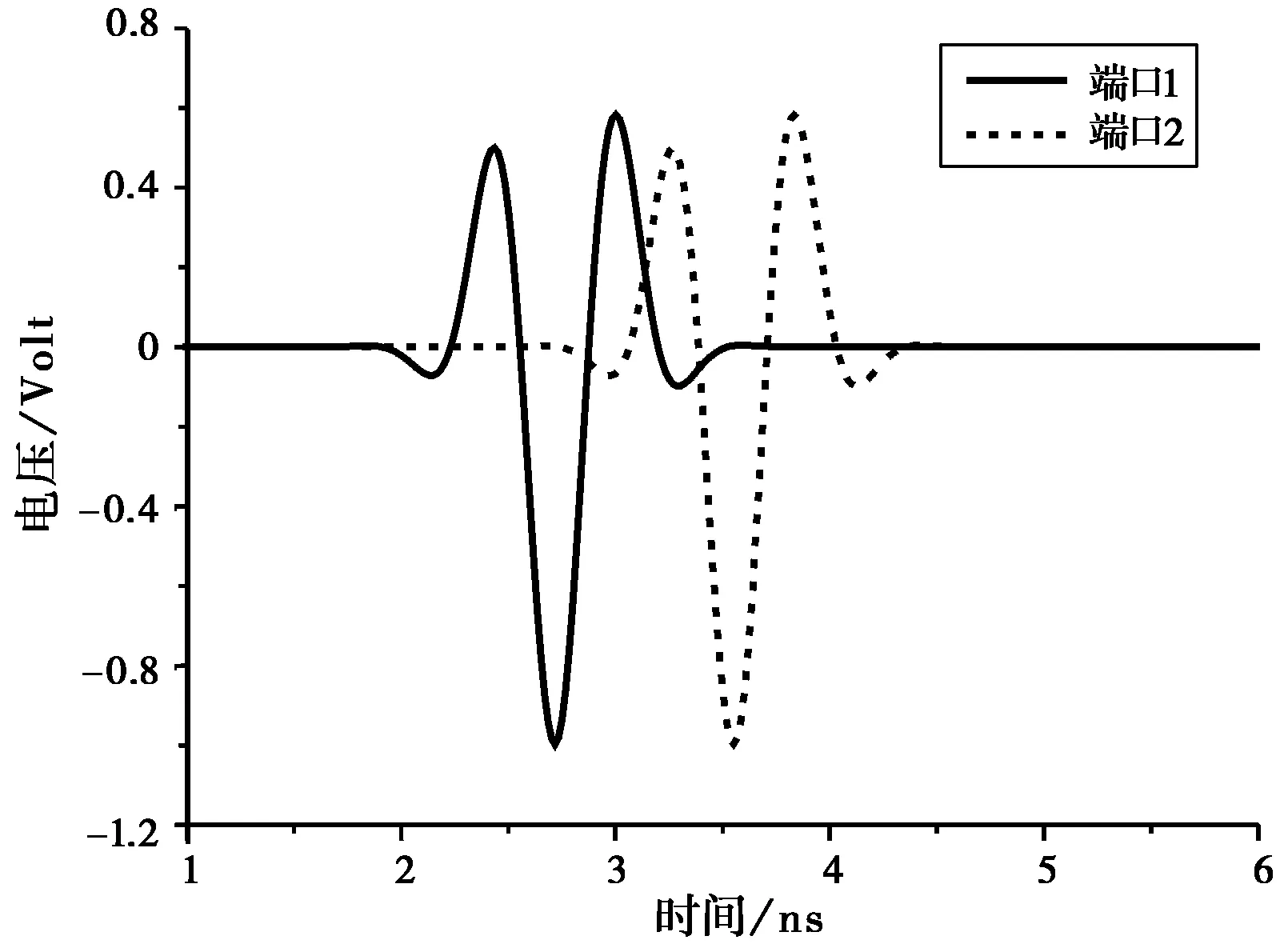
图3 调制高斯脉冲电压激励源

FDTD计算的远区辐射场及绝对增益如图 4所示(图4(a)见1023页)，增益为4.66 dB.其中(b)和(c)分别是在θ=90°和φ=0°方向上与FEKO软件(MOM算法)计算结果进行了对比，两者有较好的吻合，表明算法和程序是正确的。

算例2：六元相控圆形阵列天线，模型俯视如图 2(b)所示。计算频率f=300 MHz，振子单元长为λ/2，圆阵半径为λ/8。天线六个单元中第i个单元方位角为φi=(i-1)π/3，等副调相激励，相位分别为-42.63°，-148.38°，-148.38°，-42.63°，120.25° 和120.25°。偶极缝隙馈电各激励端口的内电阻Rs=50 Ω.

采用调制高斯脉冲激励，端口1处的电流在迭代计算至3000余步时就完全满足了收敛性的要求，如图 5(a)所示；如图 5(b)所示的是采用高斯脉冲激励端口1处的电流，其收敛速度慢，收敛性要差于用调制高斯脉冲激励的情况；如若不采用带有内阻抗Rs的电压源模型，由于馈电单元间的多次绕射及单元间的耦合作用，迭代计算万余步端口1处的电流依然不能满足收敛要求，如图 5(c)所示。可以看出本文算法对有多端口的相控阵天线的仿真分析具有重要实用价值。

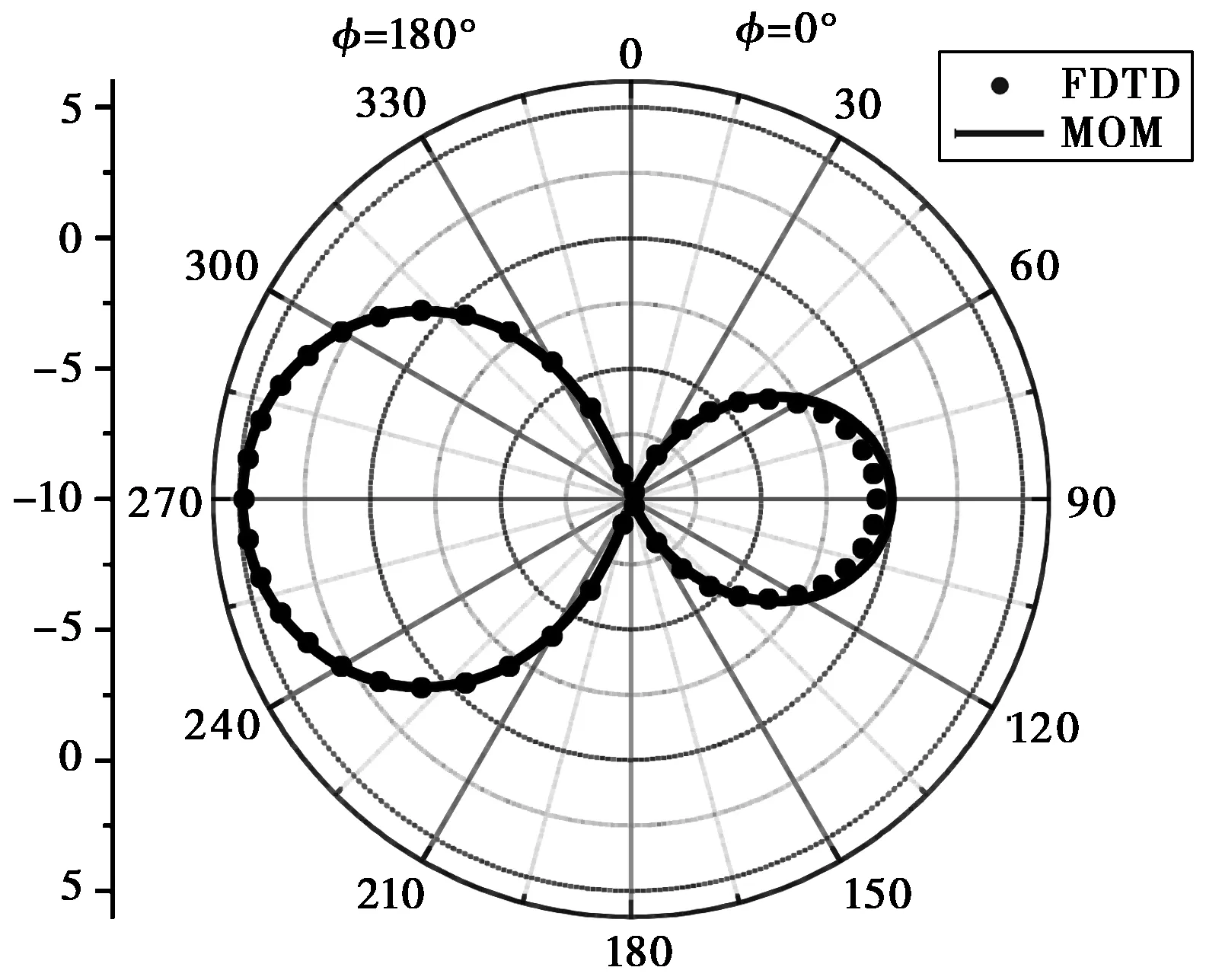
FDTD计算的远区辐射场及归一化增益如图6(图6(a)见1023页)所示，计算增益达9.67 dB，其中图 6(b)是在θ=90°的方向上计算的归一化结果，与MOM结果对比表明，除了旁瓣略存在差异外，其它吻合很好。从结果可以看出，对六元相控阵天线的六个单元相位合理设置，使得天线最大辐射方向在φ=90°位置。根据不同辐射方向的要求，控制天线阵列各馈电单元的相位，实现天线沿着任意方向进行工作的目的。

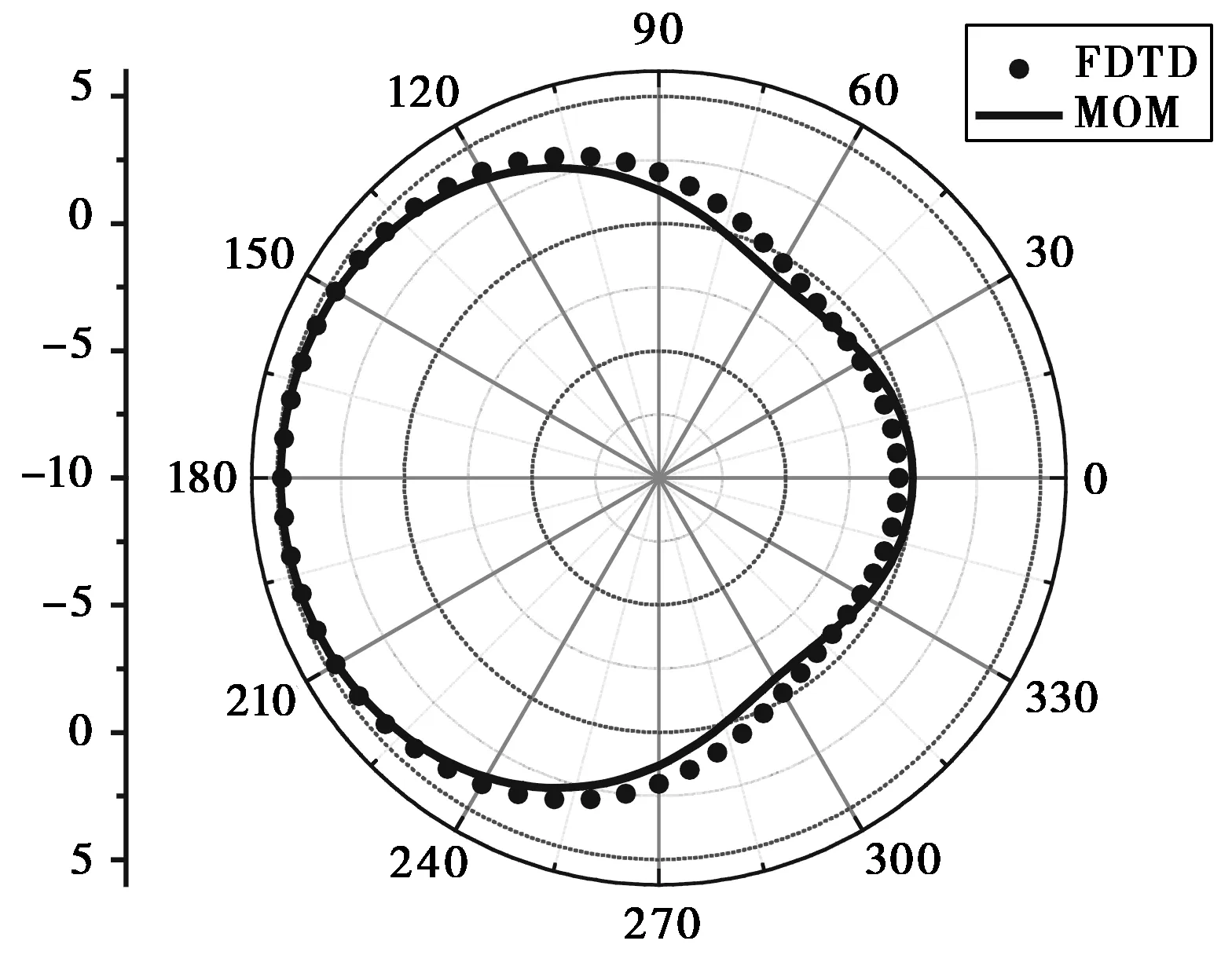
(b) θ=90°

(c) φ=0°图4 二元相控阵天线远区场及增益

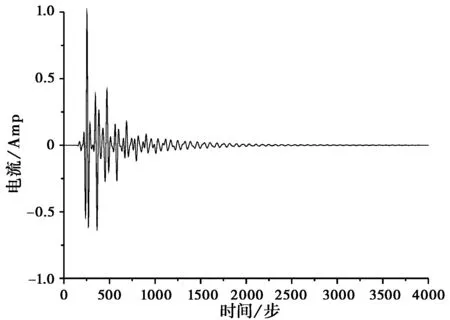
(a) Rs=50 Ω馈电模型用调制高斯脉冲激励

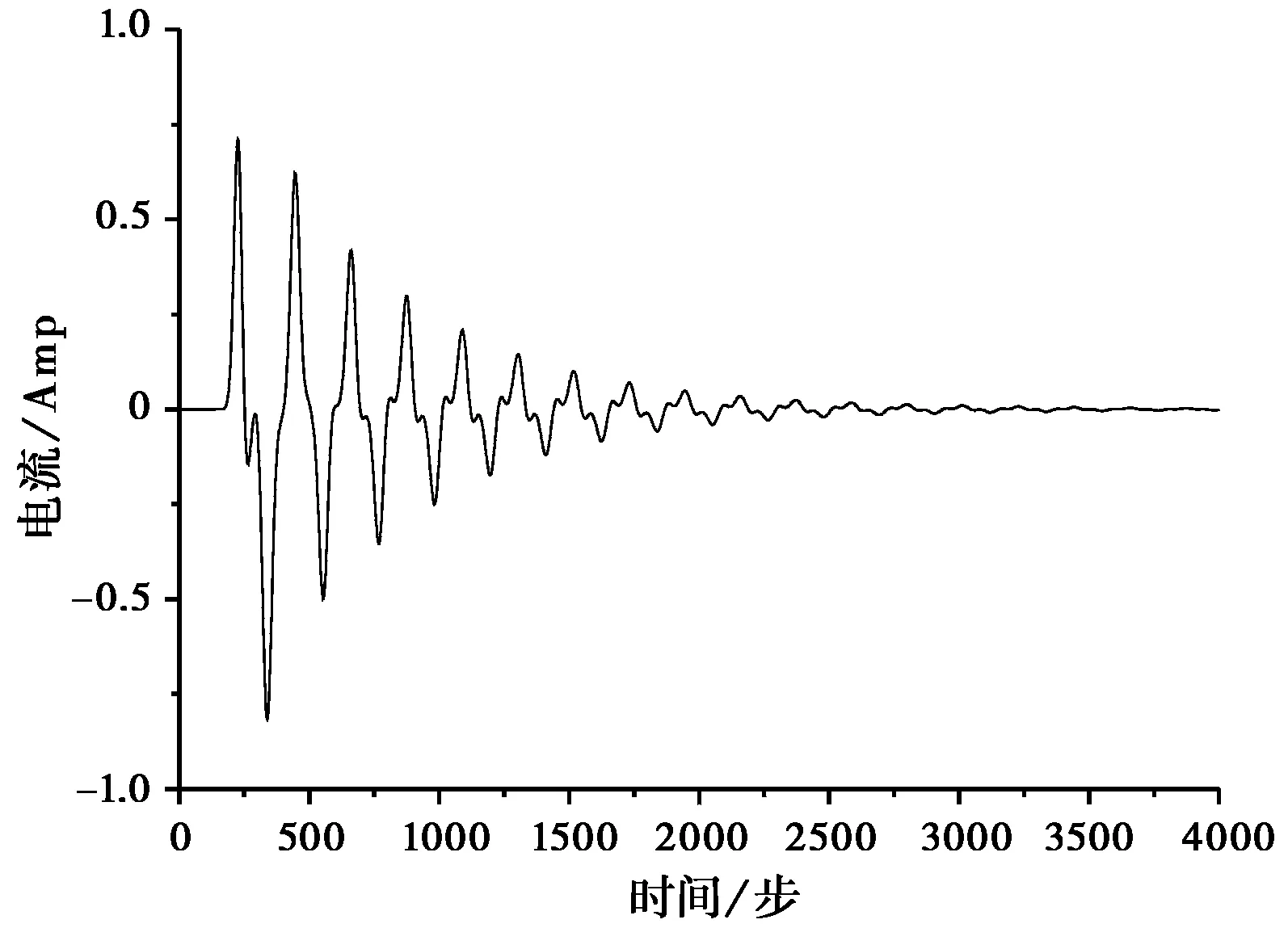
(b) Rs=50 Ω馈电模型用高斯脉冲激励

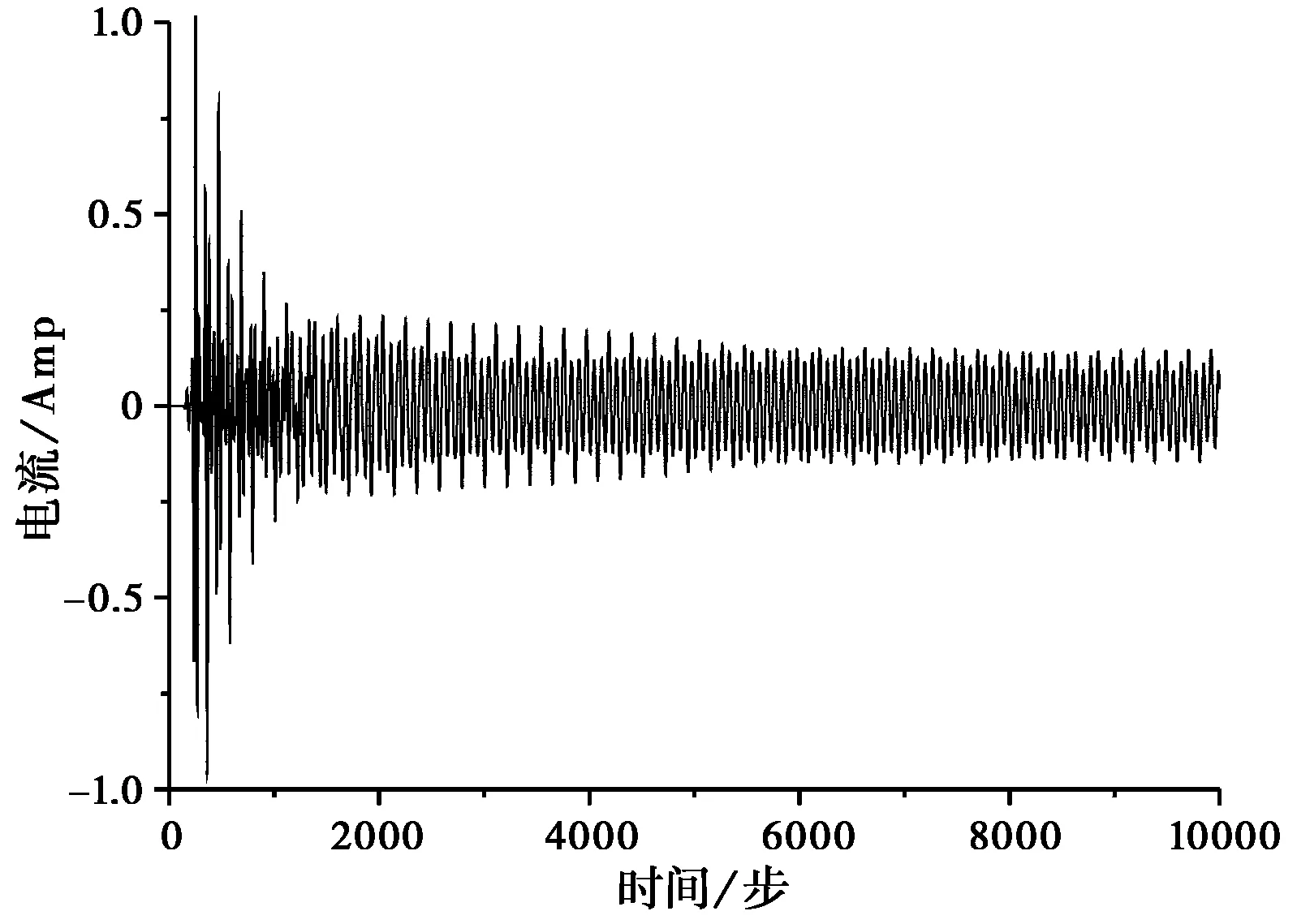
(c) 理想电压馈电模型用调制高斯脉冲激励图5 六元阵端口1处的电流

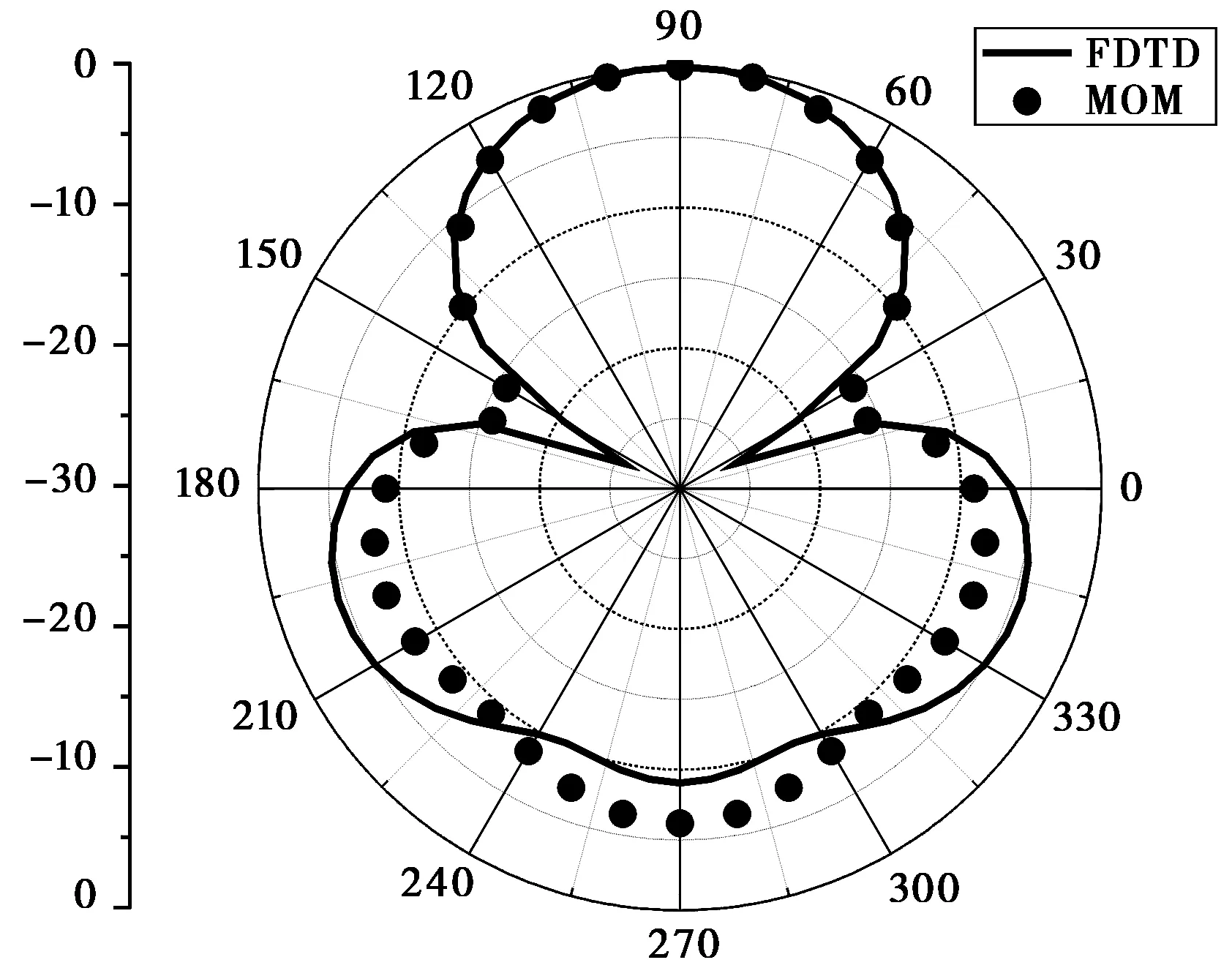
(b) θ=90°图6 六元偶极子圆形阵列天线远区场及增益

4.结 论

在FDTD方法计算相控阵天线中，在各馈电端口处通过引入带有合适时间延迟的调制高斯脉冲激励源信号，达到对天线相位进行设置的目的。为了加速FDTD数值计算收敛进程，对每一个辐射单元的馈电端口处均采用带有内电阻的偶极缝隙馈电激励源模型，有效地缩短了计算时间。

[1] YEE K S. Numerical solution of initial boundary value problems involving Maxwell equations in isotropic media[J]. IEEE Trans. Antennas Propagat., 1966, AP-14(3): 302-307.

[2] CZAWKA G., GARBARUK M. Frequency and time simulation of electromagnetic field of microwave antenna array[C]//15th International Conference on Microwaves, Radar and Wireless Communications, MIKON, 2004, 2: 469-472.

[3] 付云起, 袁乃昌, 张国华. 渐变开槽相控阵天线的FDTD分析[J]. 电波科学学报, 2001, 16(3): 334-337.

FU Yunqi, YUAN Naichang, ZHANG Guohua. FDTD analys is of tapered slot antenna arrays[J]. Chinese Journal of Radio Science, 2001, 16(3): 334-337. (in Chinese)

[4] 林 波, 王秉中, 肖绍球. 二元相控阵手机天线分析[J]. 电波科学学报, 2002, 17(3): 304-306.

LIN Bo, WANG Bingzhong, XIAO Shaoqiu. Analysis of two-element phased array handset antenna[J]. Chinese Journal of Radio Science, 2002, 17(3): 304-306. (in Chinese)

[5] 姜 文, 龚书喜, 洪 涛, 等. 新型超宽带微带天线辐射和散射特性研究[J]. 电波科学学报, 2010, 25(2): 389-392.

JIANG Wen, GONG Shuxi, HONG Tao, et al. Radiation and scattering properties of a novel UWB microstrip antenna[J]. Chinese Journal of Radio Science, 2010, 25(2): 389-392. (in Chinese)

[6] LUEBBERS R J. FDTD calculation of wide-band antenna gain and efficiency[J]. IEEE Trans. Antennas Propagat., 1992, 40(11): 1403-1407.

[7] YOSHITOMI K. A study on current sources used in finite-difference time-domain antenna analysis [C]//IEEE Applied Electromagnetics Conference, 2007: 1-4.

[8] LUEBBERS R J. LANGDON H S. A simple feed model that reduces time steps needed for FOTO antenna and microstrip calculations[J]. IEEE Trans. Antennas Propagat., 1996，44(7): 1000-1005.

[9] 葛德彪, 闫玉波. 电磁波时域有限差分法[M].2版. 西安电子科技大学出版社, 2005: 117-121.

GE Debiao, YAN Yubo. Finite-Difference Time-Domain Method for Electromagnetic Waves[M]. 2nd ed. Xidian University Press, 2005: 117-121. (in Chinese)

[10]CHEN Yikai, YANG Shiwen, LI Gang. Study of moving phase center antenna arrays using the FDTD method[C]//8th International Symposium on Antennas, Propagation and EM Theory. Chengdu, 2008: 751-754.

[11] MITRA S. Digital Signal Processing: A Computer Based Approach [M]. 3rd ed. Publishing Houses of Electronics Industry, Beijing, 2006: 95-96.